在這一頁
有機輪盤實驗
簡介
2016年9月,我聽到有人指控Interblock生產的有機輪盤賭機對輪盤計時玩家採取了激進的反制措施。作為一個公平公正博彩的倡導者,這個主題引起了我的關注。在六個月的時間裡,我參加了許多關於這個主題的會議,收集了數千次旋轉的數據。本頁講述了調查的經過。
遊戲
有機輪盤機在拉斯維加斯的許多賭場都有。它的運作方式與賭桌遊戲相同。玩家大約有30秒的時間下注。通常情況下,球會在玩家剩下1到5秒的時間時射出。下注結束後,球還需要幾秒鐘才能落地。然後,贏家將獲得賠付,整個過程將重複進行。從開始到結束大約需要一分鐘多一點的時間。
指控
如果從球發射到投注結束之間有足夠的時間,就有可能贏得比賽。投注結束前可以分析球和輪盤的速度。輪盤計時員可以估算球發射時的速度、輪盤的位置,從而預測球最終會落在輪盤的哪個位置。
我將提到這個問題的玩家稱為S先生。據他所說,娛樂型玩家可能覺得遊戲公平,因為每個號碼的中獎機率是1/38。然而,如果出現某些危險訊號,遊戲就會進入他所說的「威脅模式」。對於輪盤玩家來說,危險訊號通常包括:
- 大額賭注。 「大額」的定義尚不明確,但總計 20 美元被認為足夠了。
- 後期投注。具體來說,就是從球發出到時間窗口關閉之間的五秒鐘。
- 區域投注。對輪盤上相鄰的單一數字進行投注。
據稱,如果遊戲感到受到威脅,機器就會採取激進的反制措施。這些反制措施的目的是讓球落到輪盤計時員所設定的區域之外。具體是如何做到的尚不清楚,但 S 先生有一些理論,他要我不要透露。
S先生與我分享了他的數據和分析,這絕對足以激起我的好奇心。然而,S先生要求我不要透露任何細節。
全球遊戲博覽會
在我參與此事的早期階段,我參加了2016年在拉斯維加斯舉辦的全球遊戲博覽會。 Intellock在那裡佔據了一個非常寬敞醒目的位置。在S先生的鼓勵下,我請求與Interblock展位的一位工程師交談。最初與我互動的女銷售員找到了一位工程師,他走了過來並做了自我介紹。我坐在一台類似有機輪盤賭的機器前,這台機器在球發射後也允許玩家在大約五秒鐘內完成下注。介紹完畢後,我們的對話如下,我轉述如下:
- 沙克爾福德:我注意到在這台機器上,球在投注停止前幾秒鐘就被釋放了。
- Interblock:然後呢?
- 沙克爾福德:你不認為它容易受到計時輪盤團隊的攻擊嗎?
- Interblock:我們很清楚這個問題。
他的肢體語言和語氣表明他不想再說了,所以我感謝他抽出時間,然後高高興興地繼續前進。
按照你希望的方式理解這次談話。
第一次實驗
在聽完S先生的示範後,我非常好奇到底發生了什麼事。首先,我和另一位有興趣的人(我稱之為C先生)收集了299次旋轉的數據。我們的投注方式是每次在五個連續的數字上投注2美元。 S先生不確定總共10美元的投注是否足以讓遊戲感到威脅,但他覺得在激怒遊戲和在實驗過程中不損失太多錢之間取得了良好的平衡。
我和C先生都不是玩輪盤賭的人,所以我們會系統地投注,把投注弧的中心點作為第二輪的獲勝數字。我們的目標是看看輪盤上的獲勝位置與我們投注弧的中心點相比如何。
圖 1 和表 1 顯示了我們的中心投注位置和中獎號碼之間的每次偏移頻率。
png" />表 1
| 抵銷 | 觀察 | 期望 |
|---|---|---|
| -18 | 5 | 7.87 |
| -17 | 9 | 7.87 |
| -16 | 十三 | 7.87 |
| -15 | 7 | 7.87 |
| -14 | 11 | 7.87 |
| -13 | 12 | 7.87 |
| -12 | 7 | 7.87 |
| -11 | 10 | 7.87 |
| -10 | 8 | 7.87 |
| -9 | 10 | 7.87 |
| -8 | 6 | 7.87 |
| -7 | 8 | 7.87 |
| -6 | 9 | 7.87 |
| -5 | 10 | 7.87 |
| -4 | 3 | 7.87 |
| -3 | 7 | 7.87 |
| -2 | 7 | 7.87 |
| -1 | 6 | 7.87 |
| 0 | 8 | 7.87 |
| 1 | 4 | 7.87 |
| 2 | 4 | 7.87 |
| 3 | 8 | 7.87 |
| 4 | 7 | 7.87 |
| 5 | 4 | 7.87 |
| 6 | 18 | 7.87 |
| 7 | 6 | 7.87 |
| 8 | 9 | 7.87 |
| 9 | 6 | 7.87 |
| 10 | 8 | 7.87 |
| 11 | 4 | 7.87 |
| 12 | 十三 | 7.87 |
| 十三 | 3 | 7.87 |
| 14 | 8 | 7.87 |
| 15 | 12 | 7.87 |
| 16 | 6 | 7.87 |
| 17 | 7 | 7.87 |
| 18 | 9 | 7.87 |
| 19 | 7 | 7.87 |
| 全部的 | 299 | 299.00 |
卡方適合度檢定結果顯示,卡方統計量為45.29,自由度為37。隨機遊戲產生比此更偏斜結果的機率為16.5%。
表2顯示了在第一次實驗中,以中心數字投注為中心的各種弧長進行高斯檢驗的結果。對於我們涵蓋的五個數字的弧長,公平輪盤的預期中獎次數為39.3次。我們實際中獎次數只有29次。在公平遊戲中,出現如此糟糕或更差結果的機率為3.84%。
表 2
| 圓弧尺寸 | 觀察 | 期望 | 標準尺寸 偏差 | 標準數量 偏差 | 可能性 |
|---|---|---|---|---|---|
| 1 | 8 | 7.87 | 2.77 | 0.05 | 0.518957 |
| 3 | 18 | 23.61 | 4.66 | -1.20 | 0.114658 |
| 5 | 二十九 | 39.34 | 5.85 | -1.77 | 0.038417 |
| 7 | 四十四 | 55.08 | 6.70 | -1.65 | 0.049187 |
| 17 | 124 | 133.76 | 8.60 | -1.14 | 0.128074 |
雖然我們的結果確實低於預期,但這也可能只是普通的運氣不好。不過,我計算了一下,如果我一直以同樣的速度輸,就需要更大的樣本量來證明遊戲不公平。經過多次會議和郵件溝通,我們決定進一步進行第二次實驗。
第二次實驗
為了證明賭場遊戲不公平,必須進行可重複的實驗來證明這一點。經過大量討論,我們決定測試在五個數字組成的弧線中每個數字下注5美元,以判斷是否存在贏錢不足的情況。我們決定在三個不同的輪盤上進行1000次旋轉。除了S先生在場外,至少還有一位證人,要嘛是我,要嘛是C先生。我們決定在遊戲結束後,檢查數據並決定下一步。如果看起來我們玩的是非隨機遊戲,並且排除合理懷疑,我們計劃公開證據。
故事結束時,我們收集了1204次旋轉的數據。我們知道結果略低於預期,但據S先生說,遊戲大多時候表現都很隨機,只有部分時間處於「受威脅」模式。
根據對數據的審查,我們認為我們的損失還不足以保證繼續比賽。
以下是第二個實驗的結果和分析。首先,下面的圖表和表3顯示了球落點與球的落點之間的每次偏移頻率。
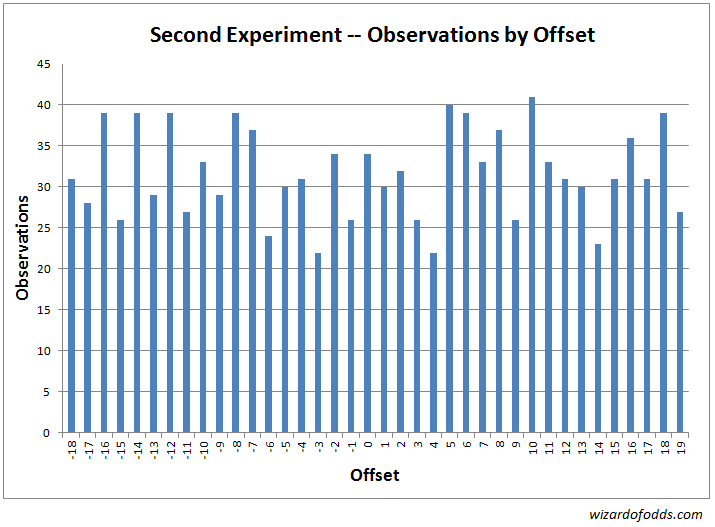
表 3
| 抵銷 | 觀察 | 期望 |
|---|---|---|
| -18 | 31 | 31.68 |
| -17 | 二十八 | 31.68 |
| -16 | 三十九 | 31.68 |
| -15 | 二十六 | 31.68 |
| -14 | 三十九 | 31.68 |
| -13 | 二十九 | 31.68 |
| -12 | 三十九 | 31.68 |
| -11 | 二十七 | 31.68 |
| -10 | 33 | 31.68 |
| -9 | 二十九 | 31.68 |
| -8 | 三十九 | 31.68 |
| -7 | 三十七 | 31.68 |
| -6 | 24 | 31.68 |
| -5 | 三十 | 31.68 |
| -4 | 31 | 31.68 |
| -3 | 22 | 31.68 |
| -2 | 三十四 | 31.68 |
| -1 | 二十六 | 31.68 |
| 0 | 三十四 | 31.68 |
| 1 | 三十 | 31.68 |
| 2 | 三十二 | 31.68 |
| 3 | 二十六 | 31.68 |
| 4 | 22 | 31.68 |
| 5 | 40 | 31.68 |
| 6 | 三十九 | 31.68 |
| 7 | 33 | 31.68 |
| 8 | 三十七 | 31.68 |
| 9 | 二十六 | 31.68 |
| 10 | 41 | 31.68 |
| 11 | 33 | 31.68 |
| 12 | 31 | 31.68 |
| 十三 | 三十 | 31.68 |
| 14 | 23 | 31.68 |
| 15 | 31 | 31.68 |
| 16 | 三十六 | 31.68 |
| 17 | 31 | 31.68 |
| 18 | 三十九 | 31.68 |
| 19 | 二十七 | 31.68 |
| 全部的 | 1204 | 1204.00 |
卡方適合度檢定結果顯示,卡方統計量為34.79,自由度為37。隨機遊戲產生比此更偏斜結果的機率為57.32%。
表4顯示了以投注中心數字為中心的各種弧長的高斯檢定結果。所有弧長均在正常範圍內。
表 4
| 圓弧尺寸 | 觀察 | 期望 | 標準尺寸 偏差 | 標準數量 偏差 | 可能性 |
|---|---|---|---|---|---|
| 1 | 三十四 | 31.68421053 | 5.55 | 0.42 | 0.661637 |
| 3 | 90 | 95.05263158 | 9.36 | -0.54 | 0.294599 |
| 5 | 156 | 158.4210526 | 11.73 | -0.21 | 0.418235 |
| 7 | 204 | 221.7894737 | 13.45 | -1.32 | 0.092997 |
| 17 | 536 | 538.6315789 | 17.25 | -0.15 | 0.439385 |
綜合結果
以下是第一次和第二次實驗的綜合數據。首先,下圖和表5顯示了弧線中心與球落地位置之間每次偏移的頻率。
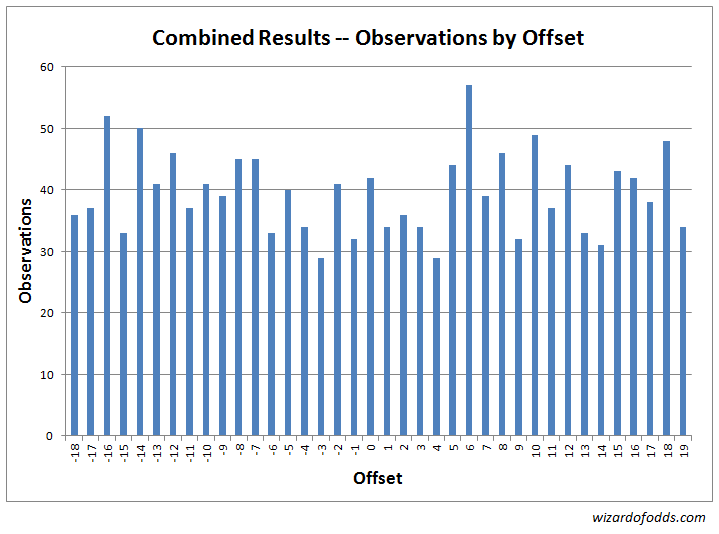
表 5
| 抵銷 | 觀察 | 期望 |
|---|---|---|
| -18 | 三十六 | 39.55 |
| -17 | 三十七 | 39.55 |
| -16 | 52 | 39.55 |
| -15 | 33 | 39.55 |
| -14 | 50 | 39.55 |
| -13 | 41 | 39.55 |
| -12 | 46 | 39.55 |
| -11 | 三十七 | 39.55 |
| -10 | 41 | 39.55 |
| -9 | 三十九 | 39.55 |
| -8 | 45 | 39.55 |
| -7 | 45 | 39.55 |
| -6 | 33 | 39.55 |
| -5 | 40 | 39.55 |
| -4 | 三十四 | 39.55 |
| -3 | 二十九 | 39.55 |
| -2 | 41 | 39.55 |
| -1 | 三十二 | 39.55 |
| 0 | 四十二 | 39.55 |
| 1 | 三十四 | 39.55 |
| 2 | 三十六 | 39.55 |
| 3 | 三十四 | 39.55 |
| 4 | 二十九 | 39.55 |
| 5 | 四十四 | 39.55 |
| 6 | 57 | 39.55 |
| 7 | 三十九 | 39.55 |
| 8 | 46 | 39.55 |
| 9 | 三十二 | 39.55 |
| 10 | 49 | 39.55 |
| 11 | 三十七 | 39.55 |
| 12 | 四十四 | 39.55 |
| 十三 | 33 | 39.55 |
| 14 | 31 | 39.55 |
| 15 | 43 | 39.55 |
| 16 | 四十二 | 39.55 |
| 17 | 三十八 | 39.55 |
| 18 | 四十八 | 39.55 |
| 19 | 三十四 | 39.55 |
| 全部的 | 1503 | 1503.00 |
卡方適合度檢定結果顯示,卡方統計量為41.75,自由度為37。隨機遊戲產生比此更偏斜結果的機率為27.19%。
表6展示了以投注中心數字為中心的不同弧長進行高斯檢驗的結果。所有測試結果均在公平遊戲的合理範圍內。
表 6
| 圓弧尺寸 | 觀察 | 期望 | 標準尺寸 偏差 | 標準數量 偏差 | 可能性 |
|---|---|---|---|---|---|
| 1 | 四十二 | 39.55263158 | 6.21 | 0.39 | 0.653346 |
| 3 | 108 | 118.6578947 | 10.45 | -1.02 | 0.153986 |
| 5 | 185 | 197.7631579 | 13.11 | -0.97 | 0.165050 |
| 7 | 248 | 276.8684211 | 15.03 | -1.92 | 0.027374 |
| 17 | 660 | 672.3947368 | 19.28 | -0.64 | 0.260114 |
第一次實驗和第二次實驗結果之間的相關係數為 0.153853。簡單來說,這意味著存在輕微的相關性,但完全在兩組隨機資料的預期範圍內。
結論
我需要非常高標準的證據才能斷言任何遊戲沒有按照公平遊戲的自然機率進行。在本案中,這項標準並未得到滿足。換句話說,我沒有理由指責有機輪盤賭機的玩法不公平。
回應
在向公眾發布之前,我邀請 S 先生預覽這個頁面。他提出了很多很好的建議和修改意見。但最終,他對我的措詞還是有些意見。所以我給了他發表回應的機會,他也照做了。回覆的標題是《S 先生對Interblock 實驗結果的另一種看法》。
我總是喜歡說最後一句話,所以我發表了一篇反駁文章,題為《對 S 先生對邁克爾·沙克爾福德的有機輪盤實驗的回應》 。



