在這一頁
為什麼二十一點中牌組數量很重要
簡介
任何可靠的二十一點資料來源都會指出,在其他條件相同的情況下,二十一點中使用的牌組數量與賭場優勢呈正相關。換句話說,牌組越少,休閒玩家的勝率就越高。對於至少具備一定知識水平,能夠貨比三家選擇規則合理的二十一點遊戲的玩家來說,這是常識。然而,我從未見過深入探討這現象的資料。本文旨在闡明這個問題。
在開始之前,我先來制定一些基本規則。考慮到2020年撰寫本文時的二十一點遊戲情況,這些規則盡可能貼近現實:
- 莊家拿到軟 17。
- 二十一點的賠率為 3 比 2。
- 發牌者以 10 或 A 為點數查看是否有黑傑克。
- 玩家可以用任兩張牌加倍。
- 玩家不得投降。
- 玩家分牌後可加倍。
- 玩家最多可以將任意一對牌(包括 A)重新拆分三次。
- 使用連續洗牌機(每手牌後洗牌)。
- 玩家使用基本策略。
我的二十一點莊家優勢計算器表明,根據這些規則,根據牌組數量,莊家優勢如下:
二十一點莊家優勢(Decks 出品)
| 甲板 | 莊家優勢 |
|---|---|
| 1 | 0.014% |
| 2 | 0.341% |
| 4 | 0.499% |
| 6 | 0.551% |
| 8 | 0.577% |
這些數字可能與其他關於二十一點的可靠資料並不完全一致。我認為任何差異都可能是由於玩家使用了切牌或使用了基於牌型的最佳策略。相較之下,我假設每手牌後都會洗牌,玩家始終遵循基於牌型的策略。
請注意,八副牌和一副牌的賭場優勢相差0.563%。本文將嘗試解答為何牌組數量對賠率有如此顯著的影響。
平衡的遊戲
首先,我考慮一個簡化的二十一點遊戲,其中玩家和莊家的規則完全相同,無論牌堆數量多少,賭場優勢均為 0%。然後,我逐步添加實際的二十一點規則,並研究它們如何隨著牌堆數量的變化而影響賭場優勢。
最初假設的簡化二十一點遊戲應具有與前面所述的相同規則,但以下情況除外:
- 玩家遵循「模仿莊家」策略。
- 贏了二十一點,賠付等額的錢。
- 如果玩家和莊家都爆牌,則結果為平手。
這個平衡遊戲中的莊家優勢顯然正好是 0.000%,因為每條規則對雙方都同樣有利。
經銷商地位優勢
在二十一點遊戲中,如果玩家和莊家都爆牌,誰會贏?莊家贏。換句話說,莊家享有位置優勢,因為先爆牌的一方輸,玩家必須先行動。這就是莊家佔優勢的原因,儘管許多規則對玩家不利。將此規則添加到平衡遊戲中,並在一副和八副牌的模擬中運行,玩家的預期收益如下。
規則變化的預期值
| 規則 | 一副甲板 | 八副牌 | 不同之處 |
|---|---|---|---|
| 經銷商位置優勢 | -8.237% | -8.157% | -0.079% |
上表顯示,在這款假設的遊戲中,玩家使用一副牌的勝率比使用八副牌的勝率更低。這是因為隨著牌組數量的減少,爆牌的機率會上升。以下是這款「模擬莊家」遊戲中爆牌的機率,假設即使玩家先爆牌,莊家也會出牌。
- 一副牌=27.333%
- 八副牌=27.209%
以上數據表明,一副牌遊戲中雙方爆牌的機率比八副牌遊戲中高0.124%。雙方爆牌之間有一定的相關性,因此,我們來分別分析一下玩家和莊家爆牌的四種組合:
破產機率
| 玩家破產 | 經銷商破產 | 一副甲板 | 八副牌 | 不同之處 |
|---|---|---|---|---|
| 不 | 不 | 44.096% | 44.468% | -0.372% |
| 不 | 是的 | 19.095% | 19.051% | 0.044% |
| 是的 | 不 | 19.095% | 19.051% | 0.044% |
| 是的 | 是的 | 8.237% | 8.157% | 0.079% |
| 全部的 | 90.524% | 90.728% | -0.204% |
機率總和不等於 100% 的原因是表格不計算雙方都有黑傑克且牌局尚未結束的情況。 「是」這一行顯示雙方都爆牌,導致莊家獲勝的情況。它表明,與八副牌相比,在單副牌遊戲中,這種情況發生的頻率高 0.080%。為什麼?如果任何一方爆牌,那一定是拿到 12 到 16 點的硬牌之後。這手牌必須至少包含兩張牌。同時,如果任何一方有兩張大牌,它就會停牌。換句話說,要牌通常發生在牌面值小於平均數值的牌中。在要牌情況下,這種小牌被拿走會導致剩餘的牌中大牌過多。在爆牌前拿走小牌的這種影響在單副牌遊戲中更為顯著。
二十一點賠率為 3 比 2
我們將添加到平衡遊戲中的下一條規則是,贏得二十一點的玩家支付 3 比 2。將該規則添加到我的模擬中將產生以下累積玩家預期回報。
- 一副牌 = -5.912%
- 八副牌 = -5.894%
為新增此規則新增一行的模擬結果表為:
規則變化的預期值
| 規則 | 一副甲板 | 八副牌 | 不同之處 |
|---|---|---|---|
| 經銷商位置優勢 | -8.237% | -8.157% | -0.079% |
| 贏家二十一點賠率為 3 比 2 | -5.912% | -5.894% | -0.018% |
計算兩行之間的差異,可以顯示贏得二十一點的玩家獲得的收益為 3 比 2:
- 一副牌=2.325%
- 八副牌=2.263%
- 差異=0.062%
這很容易用數學方法驗證,如下所示。設 d = 牌組數。使用 Excel 符號,贏得二十一點的機率為:機率(玩家二十一點)*(1-機率(莊家二十一點))= (16*d)*(4*d)/combin(52*d,2) * [1-(16*d-1)*(4*d-1)/combin(52*d-2,2)
贏得二十一點的機率
| 甲板 | 可能性 |
|---|---|
| 1 | 4.649% |
| 2 | 4.578% |
| 4 | 4.544% |
| 6 | 4.532% |
| 8 | 4.527% |
如上所示,隨著牌堆數量的減少,贏得二十一點的機率會增加。這僅僅是由於移除的影響。例如,假設第一張玩家牌是任意 10 點牌。無論牌堆數量多少,這個機率都是 4/13。很容易看出,在單副牌遊戲中,第二張牌是 A 的機率是 4/51 = 7.843%。在八副牌遊戲中,這個機率是 32/415 = 7.711%,比單副牌遊戲低 0.123%。簡單來說,在單副牌遊戲中獲得 A 的機率更高的原因是,從牌堆中移除 10 後,牌堆中的 A 會更多。如果第一張牌是 A,情況也是如此;在單副牌遊戲中,剩餘牌中的 10 會更多。
此外,如果玩家拿到黑傑克,莊家拿到黑傑克的機率會隨著牌堆數量的減少而下降。這是因為,在單副牌遊戲中,玩家從牌堆中移除一張 A 和一張 10,這使得莊家拿到黑傑克的難度遠高於八副牌遊戲。具體來說,假設玩家已經拿到黑傑克,那麼莊家拿到黑傑克的機率在單副牌中為 3.673%,在八副牌中為 4.605%。玩家每贏得一張黑傑克,就能額外贏得半個單位。要計算一張黑傑克在我們假設的平衡遊戲中以 3-2 賠付的價值,只需將贏得黑傑克的機率乘以 0.5,每次乘以額外的半個單位即可。這樣,玩家在牌堆數量上的優勢如下:
贏得二十一點的玩家優勢
| 甲板 | 玩家優勢 |
|---|---|
| 1 | 2.325% |
| 2 | 2.289% |
| 4 | 2.272% |
| 6 | 2.266% |
| 8 | 2.263% |
請注意,獲勝玩家二十一點支付額外半個單位的數學計算收益與之前顯示的單副牌和八副牌的模擬結果相符。
下表列出了目前為止所分析的規則列表,以及這些規則對於單副牌玩家相對於八副牌玩家的優勢:
規則的效力
| 規則 | 單層甲板福利 |
|---|---|
| 經銷商位置優勢 | -0.079% |
| 贏家二十一點賠率為 3 比 2 | 0.062% |
| 全部的 | -0.018% |
接下來,讓我們分析一下,當玩家被允許在 12 到 16 的硬總數上停牌時,他們會得到什麼好處。在這個範圍內,依賴總數的基本策略對於任何數量的牌組都是相同的,如下所示:
- 總數為 12 時,對莊家 4 到 6 的牌停牌,否則要牌。
- 總點數為 13 到 16 時,對莊家 2 到 6 的牌停牌,否則要牌。
將此策略加入模擬結果將產生以下玩家預期回報:
- 一副牌 = -2.209%
- 八副牌 = -2.625%
下面的模擬結果表包含新增此規則的一行:
規則變化的預期值
| 規則 | 一副甲板 | 八副牌 | 不同之處 |
|---|---|---|---|
| 經銷商位置優勢 | -8.237% | -8.157% | -0.079% |
| 贏家二十一點賠率為 3 比 2 | -5.912% | -5.894% | -0.018% |
透過第二行和第三行之間的差異可以看出,玩家在 12 到 16 的硬數字上自由選擇站立的效果。
- 一副牌=3.703%
- 八副牌=3.270%
- 差異 = 0.433%
將這兩個數字相加,可以看出,這項規則變化對單副牌遊戲玩家的影響比對八副牌遊戲玩家的影響高出0.433%。與普遍的看法相反,這解釋了為什麼單副牌遊戲比八副牌遊戲對玩家的影響高出0.563%的大部分原因。
更深入地觀察當玩家在 12 到 16 的僵局總數上停牌而莊家不能停牌時會發生什麼情況,此表顯示了由於玩家擊中較少的僵局總數而導致的各種事件給玩家帶來的好處,從而導致玩家爆牌的次數減少,莊家爆牌的次數增加,以及莊家輸掉更多對決的情況:
玩家在 12 至 16 號硬牌上停牌時可能出現的結果
| 事件 | 一副甲板 | 八副牌 | 不同之處 |
|---|---|---|---|
| 減少僅限玩家的破獲 | 6.282% | 6.271% | 0.010% |
| 更多僅針對經銷商的破產 | 4.228% | 4.171% | 0.057% |
| 較少的胸圍 | 4.228% | 4.172% | 0.055% |
| 球員贏得爭球次數減少 | -1.914% | -2.039% | 0.125% |
| 莊家贏得更多對峙 | -9.121% | -9.306% | 0.185% |
| 全部的 | 3.703% | 3.270% | 0.433% |
相同的表格已被簡化,以顯示由於莊家爆牌次數更多和輸掉更多對決而贏得更多的好處:
總結玩家在 12 至 16 號硬牌上停牌時可能出現的結果
| 事件 | 一副甲板 | 八副牌 | 不同之處 |
|---|---|---|---|
| 球員破產收益減少 | 14.738% | 14.615% | 0.123% |
| 爭球失敗 | -11.035% | -11.345% | 0.310% |
| 全部的 | 3.703% | 3.270% | 0.433% |
簡而言之,在單副牌遊戲中,如果玩家遵循基本策略,硬牌點數為12到16,爆牌的機率會比莊家低14.738%。然而,在這些牌型中,75%的情況下莊家不會爆牌,因此莊家在與16點或更少的玩家進行對決時,即使玩家無法獲勝,也能獲勝。相對於所有牌型,玩家爆牌較少可以節省14.738%,但同時會以更多對決輸錢的方式損失11.035%,因此在單副牌遊戲中,玩家的淨收益為3.703%。
在八副牌的遊戲中,這個收益只有3.270%。綜合考慮,在單副牌遊戲中,策略性地停在12到16點的收益比在八副牌遊戲中高出0.433%。
為什麼在一副牌中策略性停牌比在八副牌中更有價值?答案類似於為什麼在單副牌遊戲中莊家的位置優勢較大。在單副牌遊戲中爆牌的情況更多。雖然爆牌越多對雙方都有利,但對玩家越不利,因為雙方都爆牌時玩家就輸了。玩家停牌時,總數為 12 到 16 的牌可能由小牌組成而不是大牌。這使得牌堆中剩餘的大牌更多,有可能使玩家爆牌。在單副牌遊戲中,玩家需要拿走這些小牌來改善手牌,其代價比八副牌遊戲中更大。換句話說,在單副牌遊戲中,拿硬牌更危險。相反,在單副牌遊戲中停牌更有利。
以下是每項規則變更的成本/效益的更新表:
規則的效力
| 規則 | 單層甲板福利 |
|---|---|
| 經銷商位置優勢 | -0.079% |
| 贏家二十一點賠率為 3 比 2 | 0.061% |
| 玩家可以在硬 12 到 16 處停牌 | 0.433% |
| 全部的 | 0.415% |
玩家可以加倍
接下來,讓我們來分析一下允許加倍為玩家帶來的好處。為了研究其效果,我讓模擬根據給定的牌組數量,採用相應的加倍策略,這將在本文後面介紹。將此策略加入模擬中,玩家的預期效益如下:
- 一副牌 = -0.556%
- 八副牌 = -1.245%
這個模擬結果表包含一行用來新增此規則:
規則變化的預期值
| 規則 | 一副甲板 | 八副牌 | 不同之處 |
|---|---|---|---|
| 經銷商位置優勢 | -8.237% | -8.157% | -0.079% |
| 贏家二十一點賠率為 3 比 2 | -5.912% | -5.894% | -0.018% |
| 玩家可以在硬 12 到 16 處停牌 | -2.209% | -2.625% | 0.415% |
| 玩家可以加倍 | -0.556% | -1.245% | 0.689% |
第三行和第四行的區別體現了玩家有自由意志加倍的效果,如下:
- 一副牌=1.653%
- 八副牌=1.380%
- 差異 = 0.273%
將這兩個數字相加,可以看出,這項規則變化對單副牌遊戲玩家的影響比對八副牌遊戲玩家的影響高出0.273%。這也解釋了為什麼單副牌遊戲比八副牌遊戲對玩家的影響高出0.563%的另一個重要原因。
為什麼在單副牌遊戲中加倍更有價值?大多數情況下,玩家加倍時,硬點數在9到11點之間。加倍需要兩張牌,因此必須用兩張小於平均點數的牌才能達到9到11點的低點。如果從一副牌中取出兩張小牌,下一張牌有32.00%的機率是10,這在硬點數加倍時顯然是有利的。然而,如果從八副牌中取出兩張小牌,取出的效果就沒那麼強了,下一張牌是10的機率會降低到30.92%。
以下是每項規則變更的成本/效益更新表。請注意,0.689% 的總收益超過了最終的賭場優勢差額。這是因為我們尚未考慮分牌的影響。
規則的效力
| 規則 | 單層甲板福利 |
|---|---|
| 經銷商位置優勢 | -0.079% |
| 贏家二十一點賠率為 3 比 2 | 0.061% |
| 玩家可以在硬 12 到 16 處停牌 | 0.433% |
| 玩家可以加倍 | 0.273% |
| 全部的 | 0.689% |
玩家可以分牌
接下來,我分析了允許玩家分牌的好處。為了研究其效果,我讓模擬根據給定的牌堆數量,採用相應的分牌策略,這將在文章後面介紹。在新增此策略後,我們就得到了完整的基本策略。在添加分牌後,玩家和發牌人之間沒有其他需要研究的規則差異。在完整的基本策略中,玩家的預期效益為:
- 一副牌 = -0.012%
- 八副牌 = -0.575%
新增此規則的模擬結果表為:
規則變化的預期值
| 規則 | 一副甲板 | 八副牌 | 不同之處 |
|---|---|---|---|
| 經銷商位置優勢 | -8.237% | -8.157% | -0.079% |
| 贏家二十一點賠率為 3 比 2 | -5.912% | -5.894% | -0.018% |
| 玩家可以在硬 12 到 16 處停牌 | -2.209% | -2.625% | 0.415% |
| 玩家可以加倍 | -0.556% | -1.245% | 0.689% |
| 玩家可以分牌 | -0.012% | -0.575% | 0.563% |
第四行和第五行的差異反映了玩家有自由分牌意願的影響。
- 一副牌=0.544%
- 八副牌 = 0.669%
- 差異 = -0.125%
這兩個數字的差異表明,與八副牌遊戲相比,此規則變化對單副牌遊戲玩家的影響要低 0.125%。
在八副牌的遊戲中,分牌比一副牌更有利,因為前兩張牌組成對子的機率更大。具體來說,用Excel術語來說,八副牌的機率是13*combin(4*8,2)/combin(52*8,2) = 7.470%。一副牌的機率是13*combin(4*1,2)/combin(52*1,2) = 5.882%。
還要記住,基本遊戲規則允許最多重新分牌三次或四手牌。如果從一副牌中取出兩張相同點數的牌,那麼下一張牌出現該點數的機率為2/50 = 4.000%。而對於八副牌的牌盒來說,這個機率為30/414 = 7.246%。由於在單副牌遊戲中分牌和重新分牌的次數較少,因此分牌的整體價值較低。這解釋了為什麼從八副牌到一副牌,分牌的收益會降低。
將分牌的負面影響添加到單副牌遊戲中,完善了我們的表格,其中列出了各種規則對單副牌遊戲相對於八副牌遊戲的收益的影響。
規則 單副牌 優勢 莊家位置優勢 -0.079% 獲勝玩家黑傑克賠率為 3 比 2 0.061% 玩家可以在 12 到 16 點停牌 0.433% 玩家可以加倍 0.273% 玩家可以分牌 -0.125% 總計 0.563%請注意,右下角單元格中的 0.563% 的和與文章開頭引用的賭場優勢計算器給出的差值相符。以下是按影響順序排列的同一張表格:
規則的效力
| 規則 | 單層甲板福利 |
|---|---|
| 經銷商位置優勢 | -0.079% |
| 贏家二十一點賠率為 3 比 2 | 0.061% |
| 玩家可以在硬 12 到 16 處停牌 | 0.433% |
| 玩家可以加倍 | 0.273% |
| 玩家可以分牌 | -0.125% |
| 全部的 | 0.563% |
基本策略表
下表顯示了給定規則和一副牌的適當基本策略。
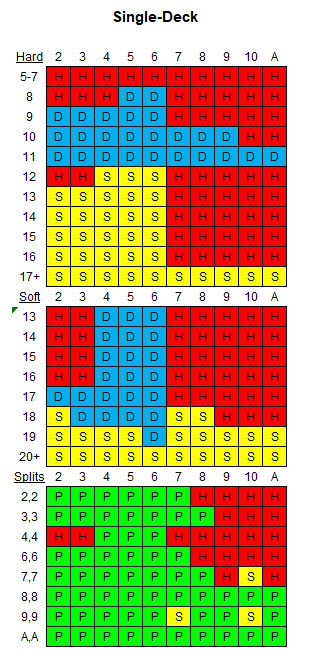
下表顯示了給定規則和八副牌的適當基本策略。
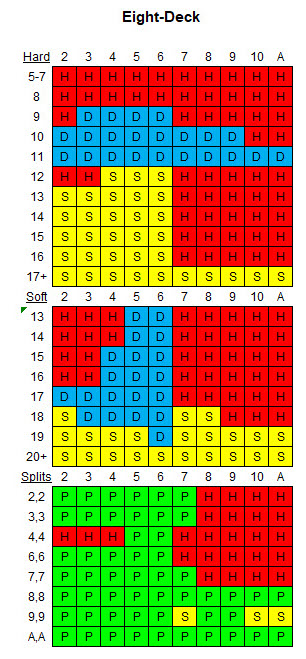
預期值表
下表顯示了單副牌遊戲中每手初始牌的預期值。最上面一行顯示莊家的明牌。預期值是在莊家檢查是否有黑傑克之前測量的。總計列顯示了根據拿到該牌的機率,每行預期值的加權平均值。右下角單元格顯示整個遊戲的預期值。
單副牌遊戲中的期望值
一副牌時玩家手牌與莊家明牌的預期值
| 玩家 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 高手 | 全部的 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 5 | -0.1278 | -0.0968 | -0.0379 | 0.0227 | 0.0403 | -0.1191 | -0.1805 | -0.2624 | -0.3654 | -0.5443 | -0.2169 |
| 6 | -0.1477 | -0.1037 | -0.0519 | 0.0104 | 0.0371 | -0.1640 | -0.2343 | -0.3046 | -0.4015 | -0.5713 | -0.2469 |
| 7 | -0.1120 | -0.0701 | -0.0119 | 0.0528 | 0.0683 | -0.0690 | -0.2232 | -0.2948 | -0.3863 | -0.5765 | -0.2211 |
| 8 | -0.0174 | 0.0199 | 0.0826 | 0.1407 | 0.1498 | 0.0921 | -0.0565 | -0.2135 | -0.3136 | -0.5144 | -0.1286 |
| 9 | 0.1124 | 0.1923 | 0.2837 | 0.3753 | 0.3799 | 0.1951 | 0.1111 | -0.0519 | -0.2165 | -0.4146 | 0.0151 |
| 10 | 0.4262 | 0.4908 | 0.5494 | 0.6276 | 0.6241 | 0.4458 | 0.3145 | 0.1644 | -0.0528 | -0.2991 | 0.2316 |
| 11 | 0.5428 | 0.5922 | 0.6516 | 0.7176 | 0.7198 | 0.4785 | 0.3417 | 0.2240 | 0.0670 | -0.1848 | 0.3268 |
| 12 | -0.2518 | -0.2255 | -0.1915 | -0.1364 | -0.1194 | -0.2273 | -0.2925 | -0.3639 | -0.4175 | -0.5824 | -0.3131 |
| 十三 | -0.2879 | -0.2411 | -0.1816 | -0.1344 | -0.1208 | -0.2861 | -0.3461 | -0.3764 | -0.4590 | -0.6106 | -0.3415 |
| 14 | -0.2900 | -0.2391 | -0.1835 | -0.1342 | -0.1209 | -0.3442 | -0.3612 | -0.4192 | -0.4957 | -0.6356 | -0.3644 |
| 15 | -0.2803 | -0.2379 | -0.1837 | -0.1388 | -0.1266 | -0.3590 | -0.4133 | -0.4703 | -0.5397 | -0.6677 | -0。3893 |
| 16 | -0.2863 | -0.2446 | -0.1872 | -0.1435 | -0.1450 | -0.3760 | -0.4254 | -0.4797 | -0.5482 | -0.6739 | -0.3978 |
| 17 | -0.1568 | -0.1216 | -0.0712 | -0.0445 | -0.0306 | -0.1217 | -0.3976 | -0.4154 | -0.4562 | -0.6560 | -0.2947 |
| 18 | 0.1072 | 0.1359 | 0.1538 | 0.1983 | 0.2031 | 0.3887 | 0.0956 | -0.1961 | -0.2242 | -0.4527 | -0.0185 |
| 19 | 0.3763 | 0.3774 | 0.3965 | 0.4449 | 0.4364 | 0.6101 | 0.5769 | 0.2642 | 0.0125 | -0.1586 | 0.2644 |
| A,2 | 0.0402 | 0.0711 | 0.1174 | 0.2130 | 0.2455 | 0.1074 | 0.0392 | -0.0141 | -0.1454 | -0.3991 | -0.0057 |
| A,3 | 0.0184 | 0.0447 | 0.1127 | 0.2042 | 0.2391 | 0.0605 | 0.0349 | -0.0602 | -0.1781 | -0.4205 | -0.0308 |
| A,4 | -0.0103 | 0.0237 | 0.0892 | 0.1753 | 0.2191 | 0.0339 | -0.0354 | -0.1136 | -0.2226 | -0.4533 | -0.0697 |
| A,5 | -0.0298 | -0.0019 | 0.0667 | 0.1490 | 0.2327 | -0.0239 | -0.0842 | -0.1666 | -0.2760 | -0.4900 | -0.1094 |
| A,6 | 0.0142 | 0.0743 | 0.1549 | 0.2805 | 0.2630 | 0.0597 | -0.0646 | -0.1348 | -0.2383 | -0.4810 | -0.0586 |
| A,7 | 0.1279 | 0.1867 | 0.3091 | 0.3482 | 0.3623 | 0.4118 | 0.1209 | -0.0873 | -0.1926 | -0.4433 | 0.0459 |
| A,8 | 0.3953 | 0.4157 | 0.4100 | 0.4593 | 0.4666 | 0.6146 | 0.6078 | 0.2882 | -0.0009 | -0.1938 | 0.2686 |
| A,9 | 0.6525 | 0.6415 | 0.6507 | 0.6810 | 0.6730 | 0.7732 | 0.7848 | 0.7656 | 0.4594 | 0.0943 | 0.5871 |
| A,10 | 1.5000 | 1.5000 | 1.5000 | 1.5000 | 1.5000 | 1.5000 | 1.5000 | 1.5000 | 1.4081 | 1.0409 | 1.4449 |
| A,A | 0.6384 | 0.6863 | 0.7417 | 0.8075 | 0.8289 | 0.6277 | 0.4865 | 0.3605 | 0.2080 | -0.1580 | 0.4744 |
| 2,2 | -0.0349 | 0.0396 | 0.1235 | 0.3014 | 0.3378 | 0.0137 | -0.1412 | -0.2224 | -0.3355 | -0.5246 | -0.1145 |
| 3,3 | -0.1082 | -0.0209 | 0.1607 | 0.3049 | 0.3395 | -0.0448 | -0.2232 | -0.3100 | -0.3986 | -0.5715 | -0.1646 |
| 4,4 | -0.0136 | 0.0268 | 0.1354 | 0.2680 | 0.2980 | 0.1104 | -0.0549 | -0.2063 | -0.3069 | -0.5065 | -0.0991 |
| 5,5 | 0.4441 | 0.5075 | 0.5870 | 0.6933 | 0.7084 | 0.4663 | 0.3227 | 0.1738 | -0.0510 | -0.2978 | 0.2444 |
| 6,6 | -0.0963 | 0.0132 | 0.1456 | 0.2786 | 0.1992 | -0.1933 | -0.3222 | -0.3862 | -0.4366 | -0.5989 | -0.2245 |
| 7,7 | -0.0546 | 0.0494 | 0.1879 | 0.2244 | 0.2396 | -0.0524 | -0.3804 | -0.4744 | -0.5556 | -0.6790 | -0.2508 |
| 8,8 | 0.1165 | 0.1873 | 0.2245 | 0.3287 | 0.3508 | 0.3040 | -0.0599 | -0.4017 | -0.4929 | -0.6389 | -0.1224 |
| 9,9 | 0.2052 | 0.2156 | 0.3070 | 0.4064 | 0.4080 | 0.4011 | 0.2067 | -0.0986 | -0.2041 | -0.4520 | 0.0666 |
| 10,10 | 0.6220 | 0.6323 | 0.6402 | 0.6718 | 0.6683 | 0.7647 | 0.7832 | 0.7440 | 0.4539 | 0.1383 | 0.5803 |
| 全部的 | 0.1021 | 0.1388 | 0.1860 | 0.2391 | 0.2471 | 0.1473 | 0.0551 | -0.0435 | -0.1712 | -0.3891 | -0.0001 |
八副牌遊戲中的期望值
八副牌中玩家手牌與莊家明牌的預期值
| 玩家 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 高手 | 全部的 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 5 | -0.1258 | -0.0929 | -0.0562 | -0.0175 | 0.018 | -0.1196 | -0.1871 | -0.266 | -0.3663 | -0.5291 | -0.2191 |
| 6 | -0.1389 | -0.1042 | -0.0677 | -0.0287 | 0.0085 | -0.1534 | -0.2192 | -0.2941 | -0.3902 | -0.5469 | -0.2395 |
| 7 | -0.1094 | -0.0760 | -0.0391 | -0.0004 | 0.0349 | -0.0689 | -0.2121 | -0.2866 | -0.3731 | -0.5526 | -0.2164 |
| 8 | -0.0234 | 0.0076 | 0.0427 | 0.0774 | 0.1079 | 0.0831 | -0.0595 | -0.2104 | -0.3079 | -0.4931 | -0.1316 |
| 9 | 0.0743 | 0.1277 | 0.1921 | 0.2580 | 0.3141 | 0.1745 | 0.0998 | -0.0522 | -0.2180 | -0.3962 | -0.0071 |
| 10 | 0.3653 | 0.4176 | 0.4704 | 0.5253 | 0.5723 | 0.3990 | 0.2895 | 0.1469 | -0.0535 | -0.2865 | 0.2056 |
| 11 | 0.4786 | 0.5264 | 0.5759 | 0.6271 | 0.6718 | 0.4653 | 0.3496 | 0.2271 | 0.0864 | -0.2297 | 0.3097 |
| 12 | -0.2535 | -0.2331 | -0.2041 | -0.1613 | -0.1208 | -0.2146 | -0.2741 | -0.3430 | -0.4273 | -0.5746 | -0.3146 |
| 十三 | -0.2867 | -0.2461 | -0.2030 | -0.1611 | -0.1210 | -0.2713 | -0.3264 | -0.3858 | -0.4682 | -0.6049 | -0.3447 |
| 14 | -0.2870 | -0.2456 | -0.2034 | -0.1612 | -0.1211 | -0.3240 | -0.3707 | -0.4295 | -0.5059 | -0.6328 | -0.3694 |
| 15 | -0.2858 | -0.2456 | -0.2033 | -0.1616 | -0.1217 | -0.3683 | -0.4162 | -0.4715 | -0.5422 | -0.6597 | -0.3927 |
| 16 | -0.2866 | -0.2463 | -0.2038 | -0.1622 | -0.1236 | -0.4103 | -0.4547 | -0.5057 | -0.5721 | -0.6820 | -0.4128 |
| 17 | -0.1565 | -0.1205 | -0.0819 | -0.0461 | -0.0090 | -0.1085 | -0.3842 | -0.4223 | -0.4633 | -0.6636 | -0.2958 |
| 18 | 0.1098 | 0.1379 | 0.1648 | 0.1953 | 0.2211 | 0.3982 | 0.1045 | -0.1847 | -0.2394 | -0.4626 | -0.0208 |
| 19 | 0.3780 | 0.3949 | 0.4138 | 0.4372 | 0.4513 | 0.6153 | 0.5918 | 0.2848 | -0.0149 | -0.1753 | 0.2569 |
| A,2 | 0.0458 | 0.0737 | 0.1041 | 0.1376 | 0.2024 | 0.1207 | 0.0523 | -0.0350 | -0.1703 | -0.3789 | -0.0269 |
| A,3 | 0.0224 | 0.0507 | 0.0827 | 0.1366 | 0.2010 | 0.0769 | 0.0155 | -0.0733 | -0.2024 | -0.4031 | -0.0533 |
| A,4 | -0.0006 | 0.0294 | 0.0641 | 0.1328 | 0.1986 | 0.0368 | -0.0282 | -0.1123 | -0.2357 | -0.4281 | -0.0803 |
| A,5 | -0.0211 | 0.0088 | 0.0611 | 0.1301 | 0.2004 | -0.0070 | -0.0689 | -0.1507 | -0.2691 | -0.4532 | -0.1057 |
| A,6 | -0.0006 | 0.0558 | 0.1220 | 0.1933 | 0.2513 | 0.0545 | -0.0721 | -0.1479 | -0.2563 | -0.4626 | -0.0792 |
| A,7 | 0.1160 | 0.1749 | 0.2418 | 0.3000 | 0.3560 | 0.4014 | 0.1074 | -0.0990 | -0.2075 | -0.4205 | 0.0270 |
| A,8 | 0.3800 | 0.3993 | 0.4157 | 0.4389 | 0.4621 | 0.6159 | 0.5953 | 0.2878 | -0.0164 | -0.1795 | 0.2579 |
| A,9 | 0.6371 | 0.6455 | 0.6562 | 0.6699 | 0.6778 | 0.7732 | 0.7909 | 0.7591 | 0.4379 | 0.1070 | 0.5752 |
| A,10 | 1.5000 | 1.5000 | 1.5000 | 1.5000 | 1.5000 | 1.5000 | 1.5000 | 1.5000 | 1.3874 | 1.0388 | 1.4309 |
| A,A | 0.6072 | 0.6561 | 0.7062 | 0.7588 | 0.8058 | 0.6277 | 0.5001 | 0.3629 | 0.2059 | -0.1511 | 0.4411 |
| 2,2 | -0.0797 | -0.0089 | 0.0697 | 0.1700 | 0.2643 | 0.0087 | -0.1576 | -0.2385 | -0.3430 | -0.5115 | -0.1430 |
| 3,3 | -0.1305 | -0.0482 | 0.0500 | 0.1502 | 0.2425 | -0.0518 | -0.2189 | -0.2946 | -0.3899 | -0.5465 | -0.1859 |
| 4,4 | -0.0225 | 0.0080 | 0.0441 | 0.1066 | 0.2027 | 0.0857 | -0.0595 | -0.2096 | -0.3070 | -0.4921 | -0.1212 |
| 5,5 | 0.3676 | 0.4201 | 0.4748 | 0.5324 | 0.5814 | 0.4012 | 0.2910 | 0.1477 | -0.0534 | -0.2863 | 0.2074 |
| 6,6 | -0.1947 | -0.0972 | 0.0043 | 0.1075 | 0.1900 | -0.2189 | -0.2775 | -0.3453 | -0.4295 | -0.5767 | -0.2426 |
| 7,7 | -0.1233 | -0.0335 | 0.0669 | 0.1569 | 0.2508 | -0.0485 | -0.3765 | -0.4361 | -0.5129 | -0.6382 | -0.2497 |
| 8,8 | 0.0720 | 0.1452 | 0.2171 | 0.3005 | 0.3753 | 0.3195 | -0.0276 | -0.3893 | -0.5170 | -0.6660 | -0.1329 |
| 9,9 | 0.1943 | 0.2506 | 0.3196 | 0.3925 | 0.4551 | 0.3996 | 0.2308 | -0.0801 | -0.2369 | -0.4624 | 0.0585 |
| 10,10 | 0.6334 | 0.6442 | 0.6549 | 0.6688 | 0.6770 | 0.7723 | 0.7907 | 0.7566 | 0.4373 | 0.1124 | 0.5745 |
| 全部的 | 0.0927 | 0.1262 | 0.1628 | 0.2025 | 0.2390 | 0.1453 | 0.0585 | -0.0403 | -0.1727 | -0.3712 | -0.0058 |
預期值的差異(%)
下表以百分比形式顯示了單副牌遊戲的預期值減去八副牌遊戲的預期值。
玩家手牌與莊家明牌的預期值變化(x100)
| 玩家 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 高手 | 全部的 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 5 | -0.196 | -0.383 | 1.834 | 4.02 | 2.229 | 0.05 | 0.664 | 0.361 | 0.087 | -1.52 | 0.22 |
| 6 | -0.8770 | 0.0480 | 1.5840 | 3.9030 | 2.8630 | -1.0640 | -1.5170 | -1.0490 | -1.1320 | -2.4330 | -0.7380 |
| 7 | -0.2560 | 0.5920 | 2.7210 | 5.3240 | 3.3400 | -0.0070 | -1.1090 | -0.8160 | -1.3150 | -2.3840 | -0.4720 |
| 8 | 0.6060 | 1.2300 | 3.9870 | 6.3300 | 4.1900 | 0.9040 | 0.3020 | -0.3070 | -0.5740 | -2.1370 | 0.2910 |
| 9 | 3.8080 | 6.4600 | 9.1610 | 11.7320 | 6.5770 | 2.0670 | 1.1320 | 0.0300 | 0.1480 | -1.8380 | 2.2220 |
| 10 | 6.0970 | 7.3170 | 7.8980 | 10.2270 | 5.1830 | 4.6820 | 2.4980 | 1.7530 | 0.0720 | -1.2510 | 2.6040 |
| 11 | 6.4200 | 6.5830 | 7.5650 | 9.0560 | 4.8030 | 1.3220 | -0.7900 | -0.3170 | -1.9460 | 4.4940 | 1.7050 |
| 12 | 0.1670 | 0.7540 | 1.2640 | 2.4890 | 0.1350 | -1.2760 | -1.8390 | -2.0880 | 0.9840 | -0.7830 | 0.1460 |
| 十三 | -0.1260 | 0.5070 | 2.1460 | 2.6670 | 0.0210 | -1.4780 | -1.9700 | 0.9410 | 0.9190 | -0.5660 | 0.3180 |
| 14 | -0.2970 | 0.6510 | 1.9930 | 2.6980 | 0.0150 | -2.0210 | 0.9460 | 1.0330 | 1.0240 | -0.2860 | 0.5000 |
| 15 | 0.5560 | 0.7690 | 1.9570 | 2.2820 | -0.4950 | 0.9270 | 0.2900 | 0.1190 | 0.2470 | -0.7990 | 0.3400 |
| 16 | 0.0300 | 0.1700 | 1.6680 | 1.8640 | -2.1330 | 3.4380 | 2.9220 | 2.6000 | 2.3870 | 0.8060 | 1.4950 |
| 17 | -0.0300 | -0.1100 | 1.0720 | 0.1630 | -2.1630 | -1.3190 | -1.3380 | 0.6910 | 0.7130 | 0.7580 | 0.1060 |
| 18 | -0.2560 | -0.2000 | -1.0990 | 0.2950 | -1.7950 | -0.9490 | -0.8890 | -1.1420 | 1.5210 | 0.9900 | 0.2340 |
| 19 | -0。1730 | -1.7470 | -1.7360 | 0.7660 | -1.4910 | -0.5200 | -1.4980 | -2.0590 | 2.7370 | 1.6770 | 0.7460 |
| A,2 | -0.5660 | -0.2590 | 1.3280 | 7.5340 | 4.3080 | -1.3290 | -1.3120 | 2.0900 | 2.4910 | -2.0210 | 2.1220 |
| A,3 | -0.4090 | -0.6000 | 3.0040 | 6.7580 | 3.8040 | -1.6410 | 1.9440 | 1.3040 | 2.4300 | -1.7440 | 2.2470 |
| A,4 | -0.9750 | -0.5720 | 2.5100 | 4.2580 | 2.0490 | -0.2980 | -0.7230 | -0.1290 | 1.3080 | -2.5210 | 1.0610 |
| A,5 | -0.8730 | -1.0720 | 0.5650 | 1.8950 | 3.2330 | -1.6930 | -1.5280 | -1.5890 | -0.6930 | -3.6740 | -0.3690 |
| A,6 | 1.4820 | 1.8480 | 3.2870 | 8.7240 | 1.1650 | 0.5180 | 0.7480 | 1.3090 | 1.7920 | -1.8340 | 2.0600 |
| A,7 | 1.1920 | 1.1830 | 6.7250 | 4.8180 | 0.6310 | 1.0410 | 1.3420 | 1.1640 | 1.4890 | -2.2860 | 1.8940 |
| A,8 | 1.5370 | 1.6390 | -0.5690 | 2.0370 | 0.4540 | -0.1320 | 1.2540 | 0.0390 | 1.5550 | -1.4310 | 1.0640 |
| A,9 | 1.5370 | -0.3990 | -0.5560 | 1.1160 | -0.4780 | 0.0020 | -0.6060 | 0.6480 | 2.1530 | -1.2700 | 1.1970 |
| A,10 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 2.0730 | 0.2070 | 1.3970 |
| A,A | 3.1200 | 3.0230 | 3.5450 | 4.8720 | 2.3070 | 0.0000 | -1.3620 | -0.2430 | 0.2140 | -0.6920 | 3.3340 |
| 2,2 | 4.4790 | 4.8510 | 5.3790 | 13.1380 | 7.3480 | 0.4980 | 1.6370 | 1.6100 | 0.7540 | -1.3140 | 2.8470 |
| 3,3 | 2.2320 | 2.7290 | 11.0750 | 15.4710 | 9.7010 | 0.7020 | -0.4300 | -1.5380 | -0.8700 | -2.4920 | 2.1250 |
| 4,4 | 0.8840 | 1.8800 | 9.1320 | 16.1400 | 9.5290 | 2.4760 | 0.4550 | 0.3380 | 0.0090 | -1.4460 | 2.2100 |
| 5,5 | 7.6550 | 8.7410 | 11.2230 | 16.0940 | 12.6990 | 6.5150 | 3.1720 | 2.6130 | 0.2380 | -1.1510 | 3.7020 |
| 6,6 | 9.8410 | 11.0360 | 14.1250 | 17.1060 | 0.9170 | 2.5610 | -4.4720 | -4.0910 | -0.7110 | -2.2180 | 1.8060 |
| 7,7 | 6.8730 | 8.2850 | 12.1030 | 6.7540 | -1.1240 | -0.3840 | -0.3830 | -3.8370 | -4.2660 | -4.0800 | -0.1170 |
| 8,8 | 4.4530 | 4.2080 | 0.7370 | 2.8160 | -2.4470 | -1.5490 | -3.2240 | -1.2460 | 2.4110 | 2.7050 | 1.0500 |
| 9,9 | 1.0910 | -3.5070 | -1.2560 | 1.3820 | -4.7120 | 0.1480 | -2.4060 | -1.8530 | 3.2860 | 1.0450 | 0.8060 |
| 10,10 | -1.1490 | -1.1970 | -1.4750 | 0.2960 | -0.8740 | -0.7630 | -0.7510 | -1.2620 | 1.6580 | 2.5910 | 0.5780 |
| 全部的 | 0.9370 | 1.2510 | 2.3110 | 3.6590 | 0.8050 | 0.1970 | -0.3390 | -0.3210 | 0.1480 | -1.7900 | 0.5620 |
進一步閱讀
彼得‧格里芬 (Peter Griffin) 的《二十一點理論》(The Theory of Blackjack) 是我看過對本文主題最精彩的闡述。他在第八章「多副牌和不同規則」中探討了這個問題,該章使用了一套不同的基準規則,併計算了一副牌和無限副牌之間的差異。他並不總是給出所有細節的確切數字,但他根據自己的假設,將 0.69% 的差異細分如下:
- 加倍下注:幾乎是 0.69% 的一半
- 玩家黑傑克:0.07%
- 分牌:超過二十一點的收益
- 站在12到16的位置:“大概是剩下的差異。”
格里芬繼續列舉了單卡牌和無限卡牌下各種規則變化的好處。
致謝
我要感謝唐‧施萊辛格 (Don Schlesinger) 對本文的分析與校對提出的明智建議。


