請問巫師 #427
蛋糕以以下方式分割:
- 第一個人獲得1%
- 第二個人獲得剩餘財產的2%。
- 第三個人獲得剩餘財產的3%。
- 等等。
誰能分到最多的蛋糕?禁止使用電子表格或窮舉法計算。
【劇透=答案】第十個人將獲得最多的蛋糕。 【劇透結束】
這是我的解決方案(PDF)。
這個問題在我的Wizard of Vegas論壇上被提出和討論。
我要感謝「Mind Your Decisions」 YouTube頻道提供的這道數學謎題。
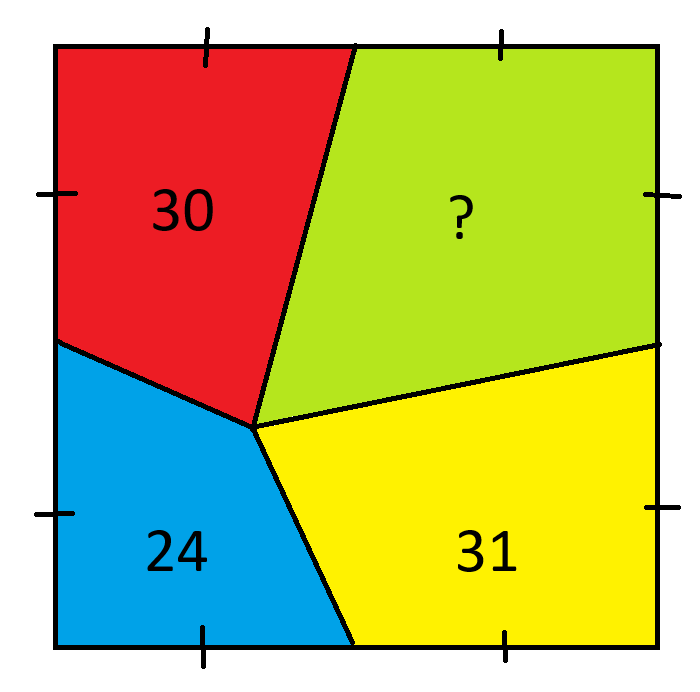
綠色區域的面積是多少?
首先,從四個圖形的交點分別向四個角落畫四條線。然後如下標記這八個圖形。
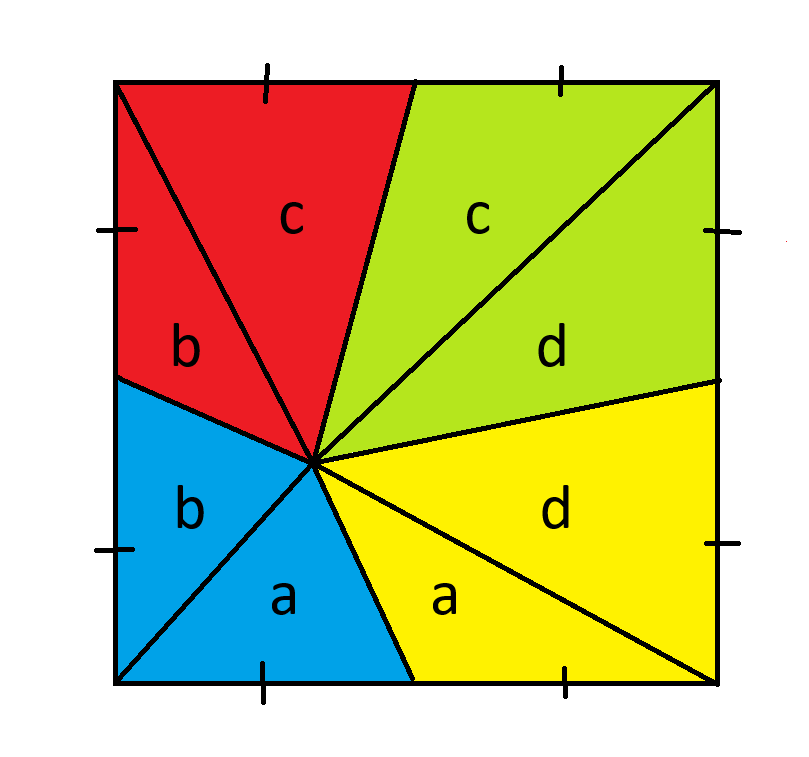
記住,三角形的面積公式是底乘以高除以2。由於所有三角形的底邊都相同,我們可以認為高度相等的三角形面積也相等。
至此我們已知:
- (1)A+B=34
- (2)B+C = 42
- (3)A+D=30
將等式(2)和(3)相加:
A+B+C+D=72
讓我們從中減去公式(1):
C+D=38,這就是我們的答案。
[劇透結束]這個問題曾經在我的Wizard of Vegas論壇上被提出和討論。
這個謎題的來源是YouTube 影片「98% 的人解不出這道數學題」。
假設你想求幾個數值的平均值。你覺得像奧運體操比賽那樣去掉最高值和最低值怎麼樣?假設目的是求某個特定街區每平方英尺的平均值。
問得好。你說的這個叫做截尾均值。我不知道有什麼統計量可以衡量截尾平均值與真實平均值之間的變異數。由於沒有更好的辦法,我自己做了一個實驗。
為了回答你的問題,我抽取了 10 萬個樣本,每個樣本包含 10 組數值。每個數值都服從標準常態分佈,即平均值為 0,變異數為 1。然後,我計算了所有 10 個數值的平均值,以及剔除部分數值後的 8 個數值的平均值。
我發現,對所有十個值進行抽樣,樣本平均值與真實平均值之間的平均差異為 0.003450。同樣地,如果取截尾平均值的平均值,則平均差異為 0.003445。我認為,這種差異不足以判斷哪種方法更好。此外,適用於我的實驗的方法可能並不適用於其他應用情境。
總之,我很少這麼說,但我沒有確切的數學答案。
對於底面為正方形或三角形的球體,哪一種堆疊方式效率較高(即最節省空間)?


我的回答方式是:當球體數量趨於無窮大時,哪一個金字塔的球體體積與包圍它們的金字塔體積之比最大。
這是我的解決方案(PDF)。
我後來發現這個問題在「問魔法師」第350期也有人問過。不過,我認為這個解決方案更好。


