在這一頁
如何計算每次投注的賭場優勢
簡介
介紹
歡迎來到擲骰子附錄。在這裡,我將推導出擲骰子所有主要投注方式的玩家優勢。在本附錄之外,我通常會討論莊家優勢,它只是玩家優勢乘以-1。為了避免每次投注都乘以-1,我將以玩家優勢的形式討論所有內容,玩家優勢可以預期為負,因為除了免費賠率之外,所有投注方式最終都由莊家擁有優勢。請稍等片刻,自己計算一下這些投注方式。這不僅能讓你更深入地理解賠率,還能激勵你更新或提升你的數學技能。
在繼續閱讀之前,你必須了解一次擲出每個點數的機率。我的骰子機率基礎頁面對此進行了深入解釋。如果你不知道或無法弄清楚擲出 6 的機率是 5/36,那麼造訪該頁面是閱讀本頁面的先決條件。
投注預期回報的一般公式是:
∑(事件 i 的機率)×(事件 i 的回報)涵蓋所有可能的結果。
玩家優勢等於預期報酬率除以初始投注。例如,在體育賽事中做反向投注時,你必須下注11美元才能贏得10美元。假設獲勝機率為50%,預期回報為0.5×(10) + 0.5×(-11) = -0.5。玩家優勢為-0.5/11 = -1/22 ≈ -4.545%。
賭場優勢規則的一個例外是平局可能出現的情況。通常,賭場優勢計算時會忽略平局。為了進行調整,當可能出現平局時,將預期回報除以已解決的平均投注額。 「已解決的平均投注額」是初始投注額與該投注被解決的機率的乘積。在擲骰子遊戲中,唯一會出現平手的投注是「不過線」和「不來」。
擲骰子遊戲中,如果一個特定事件先於另一個事件發生,很多賭注都會贏。這些賭注可能需要多次甚至更多次才能解決。如果一個賭注贏的機率為 p,輸的機率為 q,且持續有效的機率為 1-pq,那麼最終贏的機率為:
∑ p×(1-pq) i (i=0 至無窮大)=
p × (1/(1-(1-pq))) = p × (1/(p+q)) = p/(p+q)。
在本頁中,你會看到很多 p/(p+q) 形式的表達式。為了節省篇幅,我不再每次都推導出這個表達式,因為它上面已經算出來了。
傳球/來球
擲出點數獲勝的機率為 pr(7)+pr(11) = 6/36 + 2/36 = 8/36。
建立點數然後獲勝的機率是 pr(4)×pr(7 之前 4) + pr(5)×pr(7 之前 5) + pr(6)×pr(7 之前 6) + pr(8)×pr(7 之前 8) + pr(9)×pr(7 之前 9) + pr(10)×pr(9) =pr(7) 9) + pr(10)×10(
(3/36)×(3/9)+(4/36)×(4/10)+(5/36)×(5/11)+(5/36)×(5/11)+(4/36)×(4/10)+(3/36)×(3/9)=
(2/36)×(9/9 + 16/10 + 25/11)=
(2/36)×(990/990 + 1584/990 + 2250/990)=
(2/36)×(4824/990)= 9648/35640
整體獲勝機率為 8/36 + 9648/35640 = 17568/35640 = 244/495
輸的機率顯然是1-(244/495) = 251/495
因此,玩家的優勢為 (244/495)×(+1) + (251/495)×(-1) = -7/495 ≈ -1.414%。
不通過/不來
擲出結果獲勝的機率是 pr(2)+pr(3) = 1/36 + 2/36 = 3/36。
擲出結果時平手的機率為 pr(12) = 1/36。
建立點數並獲勝的機率為 pr(4)×pr(4 之前 7) + pr(5)×pr(5 之前 7) + pr(6)×pr(6 前 7) + pr(8)×pr(8 之前 7) + pr(9)×pr(9 之前 7) + pr(10)×pr(9) =pr(9 之前 7) + pr10)×pr7(
(3/36)×(6/9)+(4/36)×(6/10)+(5/36)×(6/11)+(5/36)×(6/11)+(4/36)×(6/10)+(3/36)×(6/9)=
(2/36)×(18/9 + 24/10 + 30/11)=
(2/36)×(1980/990 + 2376/990 + 2700/990)=
(2/36)×(7056/990)= 14112/35640
總獲勝機率為 3/36 + 14112/35640 = 17082/35640 = 2847/5940
輸的機率是 1-(2847/5940 + 1/36) = 1-(3012/5940) = 2928/5940
預期收益為 2847/5940×(+1) + 2928/5940×(-1) = -81/5940 = -3/220 ≈ 1.364%
大多數其他關於擲骰子的資料都聲稱,不及格投注的賭場優勢是 1.403%。造成這種差異的原因在於是否計算平局。我傾向於將平局算作金錢投注,而其他人則不這麼認為。我不是說哪一方是對是錯,只是我比較喜歡計算平手。如果您不將平局算作金錢投注,則應將上述數字除以投注結果為贏或輸的機率 (35/36)。因此,1.364%/(35/36) ≈ -1.403%。這是假設玩家在開局擲骰中從未擲出 12 點的情況下的賭場優勢。
下注贏錢
押註 6 或 8:[(5/11)×7 + (6/11)×(-6)]/6 = (-1/11)/6 = -1/66 ≈ -1.515%
押注 5 或 9:[(4/10)×7 + (6/10)×(-5)]/5 = (-2/10)/5 = -1/25 = -4.000%
押注 4 或 10:[(3/9)×9 + (6/9)×(-5)]/5 = (-3/9)/5 = -1/15 ≈ -6.667%
下注輸
押注 6 或 8 輸:[(6/11)×4 + (5/11)×(-5)]/5 = (-1/11)/5 = -1/55 ≈ -1.818%
押注 5 或 9 輸:[(6/10)×5 + (4/10)×(-8)]/8 = (-2/10)/8 = -1/40 = -2.500%
押注 4 或 10 輸:[(6/9)×5 + (3/9)×(-11)]/11 = (-3/9)/11 = -1/33 ≈ -3.030%
注意:實體賭場不允許此類投注。只有部分網路賭場允許此類投注。
買
買入押注 6 或 8:[(5/11)×23 + (6/11)×(-21)]/21 = (-11/11)/21 = -1/21 ≈ -4.762%
買入押注 5 或 9:[(4/10)×29 + (6/10)×(-21)]/21 = (-10/10)/21 = -1/21 = -4.762%
買入押注 4 或 10:[(3/9)×39 + (6/9)×(-21)]/21 = (-9/9)/21 = -1/21 ≈ -4.762%
萊伊
押注 6 或 8 輸:[(6/11)×19 + (5/11)×(-25)]/25 = (-11/11)/25 = -1/25 ≈ -4.000%
押注 5 或 9 輸:[(6/10)×19 + (4/10)×(-31)]/31 = (-10/10)/31 = -1/31 = -3.226%
押注 4 或 10 輸:[(6/9)×19 + (3/9)×(-41)]/41 = (-9/9)/41 = -1/41 ≈ -2.439%
六大/八大
[(5/11)×1 + (6/11)×(-1)]/1 = -1/11 ≈ 9.091%
硬4/硬10
注意:硬 4 和硬 10 的賠率為 7比1,或 8比1。在擲骰子遊戲中,布上的賠率以 1 為基礎列出,包括上面的圖表。
任何給定擲骰子時出現硬 4 的機率為 1/36。
任何給定擲骰子出現 7 的機率是 6/36。
任何給定擲骰子時出現軟 4 的機率為 2/36(1+3 和 3+1)。
任何一次擲骰子獲勝的機率都是 1/36。
任何擲骰子失敗的機率是 6/36 + 2/36 = 8/36。
贏得賭注的機率是 p/(p+q)(見上文)= (1/36)/(9/36) = 1/9
預期回報率為 (1/9)×7 + (8/9)×(-1) = -1/9 ≈ 11.111%。
由於賭注為 1 個單位,因此玩家的優勢也是 -1/9。
對於硬 10,賠率是相同的。
硬6/硬8
注意:硬 4 和硬 10 的賠率為 9比1,或 10比1。在擲骰子遊戲中,布上的賠率以 1 為基礎列出,包括上面的圖表。
任何一次擲骰子出現硬 6 的機率都是 1/36。
任何給定擲骰子出現 7 的機率是 6/36。
任何給定擲骰子時出現軟 6 的機率為 4/36(1+5、2+3、3+2 和 5+1)。
任何一次擲骰子獲勝的機率都是 1/36。
任何擲骰子失敗的機率是 6/36 + 4/36 = 10/36。
贏得賭注的機率是 p/(p+q)(見上文)= (1/36)/(11/36) = 1/11
預期回報率為 (1/11)×9 + (10/11)×(-1) = -1/11 ≈ 9.091%。
由於賭注為 1 個單位,因此玩家的優勢也是 -1/11。
對於硬 8,賠率是相同的。
擲骰子 2/擲骰子 12
[(1/36)×30 + (35/36)×(-1)]/1 = -5/36 ≈ -13.889%
擲骰子 3/擲骰子 11
[(2/36)×15 + (34/36)×(-1)]/1 = -4/36 ≈ -11.111%
任何擲骰子
[(4/36)×7 + (32/36)×(-1)]/1 = -4/36 ≈ -11.111%
任意 7
[(6/36)×4 + (30/36)×(-1)]/1 = -6/36 ≈ -16.667%
喇叭
擲出 2 或 12 的機率是 1/36 + 1/36 = 2/36。
擲出 3 或 11 的機率是 2/36 + 2/36 = 4/36。
擲出其他點數的機率為 1-2/36-4/36 = 30/36。
記住,角注就像四種骰子賭注合而為一。即使其中一個贏了,其他三個仍然輸。賭場優勢如下:
[(2/36)×27 + (4/36)×12 + (30/36)×(-4)]/4 = (-18/36)/4 = 12.500%
場地
當 12 支付 2:1 時,預期回報為:
2×(pr(2)+pr(12)) + 1×(pr(3)+pr(4)+pr(5)+pr(10)+pr(11)) + -1×(pr(6)+pr(7)+pr(8)+pr(9)) =
2×(1/36 + 1/36) + 1×(2/36 + 3/36 + 4/36 + 3/36 + 2/36) + -1×(5/36 + 6/36 + 5/36 + 4/36) =
2×(2/36) + 1×(14/36) + -1×(20/36) = -2/36 = -1/18 ≈ 5.556%。
當 12 支付 3:1 時,預期回報為:
3×pr(2) + 2×pr(12)) + 1×(pr(3)+pr(4)+pr(5)+pr(10)+pr(11)) + -1×(pr(6)+pr(7)+pr(8)+pr(9)) =
3×(1/36) + 2×(1/36) + 1×(2/36 + 3/36 + 4/36 + 3/36 + 2/36) + -1×(5/36 + 6/36 + 5/36 + 4/36) =
3×(1/36) + 2×(1/36) + 1×(14/36) + -1×(20/36) = -1/36 ≈ 2.778%。
購買賠率
4 和 10:[(3/9)×2 + (6/9)×(-1)]/1 = 0.000%
5 和 9:[(4/10)×3 + (6/10)×(-2)]/2 = 0.000%
6 和 8:[(5/11)×6 + (6/11)×(-5)]/5 = 0.000%
賠率
4 和 10:[(6/9)×1 + (3/9)×(-2)]/1 = 0.000%
5 和 9:[(6/10)×2 + (4/10)×(-3)]/2 = 0.000%
6 和 8:[(6/11)×5 + (5/11)×(-6)]/5 = 0.000%
綜合通行證和購買賠率
透過賠率和買入賠率組合的玩家優勢等於玩家平均收益除以玩家平均投注。通過線的收益始終為 -7/495,而賠率的收益始終為 0。預期投注額取決於您允許的賠率倍數。假設全雙倍賠率,即透過線投注為 2 美元,4、5、9 和 10 的賠率投注為 4 美元,6 或 8 的賠率投注為 5 美元。
平均增益為-2×(7/495) = -14/495。
平均投注金額為 2 + (3/36)×4 + (4/36)×4 + (5/36)×5 + (5/36)×5 + (4/36)×4 + (3/36)×4] =
2 + 106/36 = 178/36
玩家優勢為 (-14/495)/(178/36) = -0.572%。
如果 6 和 8 的賠率乘以 x,5 和 9 的賠率乘以 y,4 和 10 的賠率乘以 z,則一般公式為 (-7 / 495) / [ 1 + ((5x + 4y + 3z) / 18) ]
不通過賠率和下注賠率的組合
玩家在不及格賠率和下注賠率組合中的贏利等於玩家平均贏利除以玩家平均投注。不及格賠率的贏利始終為-3/220,而賠率的贏利始終為0。預期投注額取決於您允許的賠率倍數。假設賠率翻倍,不及格投注額為10美元。那麼玩家可以投注40美元,在4和10上贏得20美元;投注30美元,在5和9上贏得20美元;投注24美元,在6和8上贏得20美元。平均贏利為-10×(3/220) = -30/220。
平均賭注為 10 + 2×[(3/36)×40 + (4/36)×30 + (5/36)×24] = 30。
玩家優勢為 (-30/220)/30 = -0.455%。
一般公式是,如果您可以購買 x 倍賠率,那麼組合不通過和下注賠率的莊家優勢是 (3/220)/(1+x)。
每場淨收益/損失
下表顯示了100次嘗試或最終擲出結果(come out rolls)後預期的淨盈虧。為了方便繪製圖表,假設玩家在過線(pass line)上投注1美元,並接受雙倍賠率。
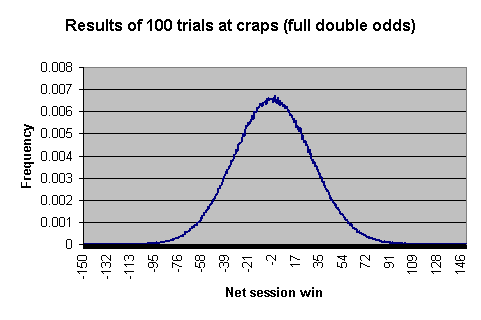
這裡有一些實際數字,顯示了落入各個區間的機率。
會話贏/輸
| 間隔 | 可能性 |
|---|---|
| 損失超過100美元 | 0.0422% |
| 損失 76 至 100 美元 | 0.6499% |
| 損失 51 至 75 美元 | 4.6414% |
| 損失 26 至 50 美元 | 16.3560% |
| 損失 1 至 25 美元 | 30.0583% |
| 收支平衡 | 0.6743% |
| 贏取 1 至 25 美元 | 28.6368% |
| 贏取 26 至 50 美元 | 14.4257% |
| 贏取 51 至 75 美元 | 3.9097% |
| 贏取 76-100 美元 | 0.5639% |
| 贏得超過 100 美元 | 0.0418% |
此圖表和表格是透過模擬 1,000,000 次 100 次試驗或擲骰子並將每次試驗的結果製成表格而創建的。
內部連結
- 簡言之,每次下注的莊家優勢是如何得出的。
- 所有主要賭注的賭場優勢(按每次下注和每次擲骰計算)
- 骰子控制實驗。兩項關於擲骰子技巧的實驗結果。
- 骰子控制優勢。假設玩家能夠影響骰子,則玩家擁有優勢。
- 擲骰子變體。替代規則和賭注,例如 Fire Bet、Crapless Craps 和 Card Craps。
- 加州擲骰子遊戲。加州人使用撲克牌來玩擲骰子遊戲。
- 玩擲骰子。在聖地牙哥的 Viejas 賭場使用紙牌玩擲骰子遊戲。
- 擲骰次數表。擲骰者在擲出七點前堅持擲 1 至 200 次的機率。
- 問問巫師。看看我回答的擲骰子問題:
- 簡單的擲骰子遊戲。我的簡單 Java 擲骰子遊戲。


