電視遊戲節目 - 常問問題
這並不完全算是賭博,但我一直想知道在《價格猜猜樂》遊戲節目中,當你不是最後一個旋轉大輪盤的人時,最佳策略是什麼。假設你無法控制旋轉結果(完全隨機),每次旋轉結果以5美分為增量,從0.05美元到1.00美元不等,你可以選擇旋轉一次或兩次,但總和不能超過1.00美元。那麼,當你第一次旋轉後達到多少金額時,你應該放棄第二次旋轉,以便有最大的機會擊敗在你之後旋轉的玩家?
第一位玩家如果第一次旋轉獲得65美分或更少,應再次旋轉。
若以下任一條件成立,第二位玩家應再次旋轉。
- 他的分數低於第一位玩家的分數。
- 他的分數是50分或更低。
- 他的分數是65分或更低,並且他與第一位玩家並列。
價格猜猜看 (Price is Right) 遊戲中Plinko遊戲的最佳策略是什麼?
從左到右,獎金分別為 100 美元、500 美元、1000 美元、0 美元、10000 美元、0 美元、1000 美元、500 美元、100 美元。我需要知道棋盤上棋子的確切排列才能進行完美的分析,但僅憑目測棋盤(請參閱上面的連結),我強烈認為玩家應該將冰球直接扔到 10,000 美元的獎金上。雖然它以兩個零為界,但其他所有獎金與最高獎金相比都黯然失色。因此,玩家的策略應該是將冰球直接扔到上面,以最大化獲得最高獎金的機率。為了證實或否定我的假設,我進行了搜索,發現有很多連結致力於研究這個遊戲。這個( www.amstat.org/publications/jse/v9n3/biesterfeld.html )是其中一個比較好的鏈接,它與我的結論一致。其中部分內容指出,將冰球投到中間的預期價值為 2557.91 美元,投到中間兩側的預期價值為 2265.92 美元,並且隨著遠離中心而逐漸減少。
在遊戲節目《讓我們來做個交易》中,有三扇門。舉例來說,假設兩扇門後是山羊,一扇門後是一輛新車。主持人蒙提·霍爾挑選了兩位參賽者來選擇一扇門。每次蒙提都會先打開一扇門,展示門後的山羊。假設這次打開的是第一位參賽者選擇的門。雖然蒙提實際上從未這樣做過,但如果此時他給另一位參賽者一個機會,可以換到另一扇未開啟的門,這位參賽者應該換嗎?
是的!這個問題的關鍵在於主持人注定會打開一扇有山羊的門。他知道哪扇門後有汽車,因此無論玩家選擇哪扇門,他總能先揭示一隻山羊。這個問題被稱為「蒙提霍爾悖論」。之所以會產生許多困惑,往往是因為在問題描述時,未能明確說明主持人知道汽車的位置,並且總是先揭示一隻山羊。我認為這部分責任要歸咎於瑪麗蓮·沃斯·莎凡特,她在專欄中對問題的描述不佳。假設獎品在1號門後,以下是玩家(第二位參賽者)採取不換門策略時會發生的情況。
- 玩家選擇了門1 --> 玩家勝利
- 玩家選擇了門2 --> 玩家輸了
- 玩家選擇了門3 --> 玩家輸了
若玩家採取換門策略,將會發生以下情況。
- 玩家選擇了門1 --> 主持人揭示門2或門3後的山羊 --> 玩家切換到另一扇門 --> 玩家失敗
- 玩家選擇了門2 --> 主持人揭露了門後的山羊在第三扇門 --> 玩家轉換到門1 --> 玩家勝利
- 玩家選擇了門3 --> 主持人揭露了門2後面的山羊 --> 玩家轉換到門1 --> 玩家勝利
因此,不換門的話,玩家有1/3的獲勝機會。而選擇換門,玩家的獲勝機會則提升至2/3。所以玩家絕對應該選擇換門。
若要進一步了解蒙提霍爾悖論,推薦閱讀維基百科上的相關文章。
我的問題是關於一個被稱為“雙信封悖論”的問題。你正在參加一個遊戲節目。你面前有兩個信封,每個信封裡都裝著未知的現金。你被告知其中一個信封裡的錢是另一個信封的兩倍。現在你被要求選擇一個信封。你選了一個,裡面裝著5萬美元。現在你被告知你可以保留你選的信封,或換成另一個。你應該換嗎?如果你事先知道你可以換,那麼換不換就無所謂了,因為你只需要選擇你最終想要的那個信封。但是,因為你是在選擇信封之後才知道可以換,所以最初的選擇和換信封的選擇是兩個獨立事件,對嗎?也就是說,在決定是否要換信封時,另一個信封裡的錢要不是你目前金額的兩倍,就是你目前金額的一半。所以它要嘛是10萬美元,要嘛是2.5萬美元。由於兩種情況發生的機率都是50%,所以另一個信封的預期價值是62,500美元。一般來說,如果我們讓 x = 你最初選擇的金額,那麼另一個信封的期望值就是 1.25 倍。因此,交換總是正確的。這樣對嗎?謝謝。
我對這個問題非常熟悉。我在我的數學題網站上,也就是第6題裡提到過。在那裡,我討論了一般情況,包括完全不查看第一個信封。但是,要回答你的問題,我們不能忽略遊戲的場地。你說這是一檔「遊戲節目」。在大多數遊戲節目中,5萬美元已經是一筆不錯的獎金了。但《價格猜猜猜》(Price is Right)節目中,很少有選手能贏到這麼高的獎金。我猜《誰想成為百萬富翁》(Who Wants to be a Millionaire)節目中,只有不到50%的選手能贏到這麼高的獎金。同時,2.5萬美元的獎金在遊戲節目中並不罕見。在《價格猜想》(Price is Right)節目中,汽車的中獎率通常都在2.5萬美元左右。在《誰想成為百萬富翁》(Who Wants to be a Millionaire)節目中,3.2萬美元的中獎率也很常見。 《危險邊緣》(Jeopardy)節目中,每個節目的平均獎金約為2.5萬美元。偉大的肯·詹寧斯(Ken Jennings)在74場勝利中,平均只贏了34,091美元。所以,我的觀點是,對於遊戲節目來說,贏得5萬美元已經很不錯了,贏得10萬美元的機率遠低於贏得2.5萬美元。因此,身為遊戲節目鑑賞家,我認為另一個信封裡更有可能裝2.5萬美元,而不是10萬美元。所以,我認為在你的例子中,最好保留5萬美元。這也表明,你永遠不能假設另一個信封裡裝的是一半或兩倍金額的機率恰好是50%。一旦你了解了金額,並結合比賽場地的情況,你就能做出明智的換信封決定,這樣1.25倍的論點就不攻自破了。
我的問題是關於一檔名為「一擲千金」的遊戲節目,這檔節目在澳洲非常受歡迎,即將登陸英國。節目中,參賽者需要面對26個編號的公事包,每個公事包裡都藏有一定數量的錢,金額從50美分到20萬美元不等,具體金額如下。
- 0.50 美元
- 1美元
- 2美元
- 5美元
- 10美元
- 25美元
- 50美元
- 75美元
- 100美元
- 150美元
- 250美元
- 500美元
- 750美元
- 1,000美元
- 1,500美元
- 2,000 美元
- 3,000 美元
- 5,000 美元
- 7,500 美元
- 10,000美元
- 15,000美元
- 3萬美元
- 5萬美元
- 75,000美元
- 10萬美元
- 20萬美元
參賽者從中選擇公事包作為自己的箱子。透過排除法,他們打開其他箱子,試圖計算自己的箱子裡有多少錢,或者是否更明智地接受「銀行出價」。銀行出價是基於剩餘公文包的算術平均值,但不等同於該平均值。因此,如果剩餘的公文包大多是高價值的,那麼參賽者的公文包很可能很有價值,因此銀行出價會很高。相反,如果玩家運氣不好,打開了價值較高的公事包,那麼銀行出價就會很低。如果你是這個遊戲的參賽者,最佳策略是什麼?一個非數學直覺策略是忽略銀行出價,繼續打開箱子,直到20萬美元被打開並消除,或者10萬美元和7.5萬美元都被打開並消除。巫師,這個遊戲背後的數學原理是什麼?
「一擲千金」剛在美國開始。規則聽起來一樣,只是我們的獎金最高可達一百萬美元,具體如下。
- 0.01
- 1
- 5
- 10
- 二十五
- 50
- 75
- 100
- 200
- 300
- 400
- 500
- 750
- 1000
- 5000
- 10000
- 25000
- 5萬
- 75000
- 100000
- 20萬
- 30萬
- 40萬
- 50萬
- 750000
- 1000000
遊戲流程如下:
- 玩家為自己選擇一個案例
- 玩家打開剩餘 25 個箱子中的 6 個。
- 銀行家提出報價。
- 如果玩家拒絕,他會再打開剩餘 19 個箱子中的 5 個。
- 銀行家提出報價。
- 如果玩家拒絕,他會再打開剩餘 14 個箱子中的 4 個。
- 銀行家提出報價。
- 如果玩家拒絕,他會再打開剩餘 10 個箱子中的 3 個。
- 銀行家提出報價。
- 如果玩家拒絕,他會再打開剩餘 7 個箱子中的兩個。
- 銀行家提出報價。
- 如果玩家拒絕,他會再打開剩下的一個箱子。
- 不斷重複步驟 11 和 12,直到玩家接受報價或玩家擁有最後一個未打開的盒子。
下圖描繪了玩家的期望值和銀行家的報價。
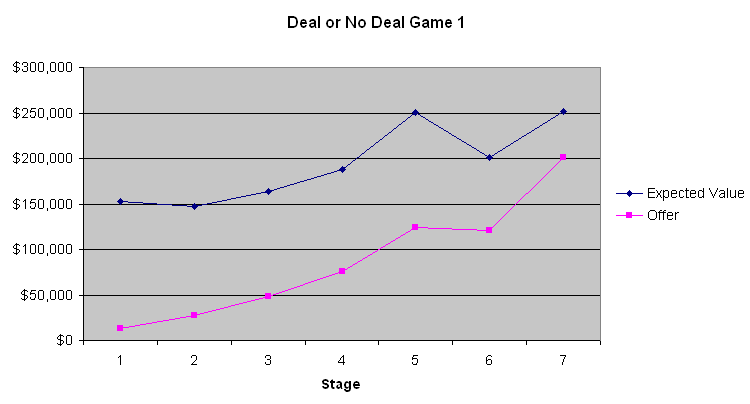
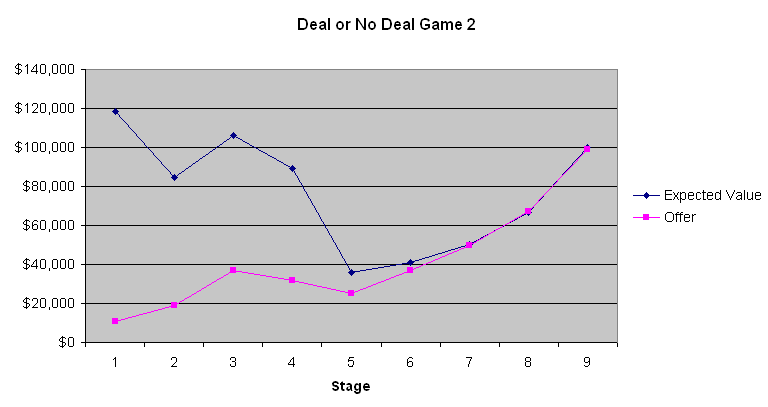
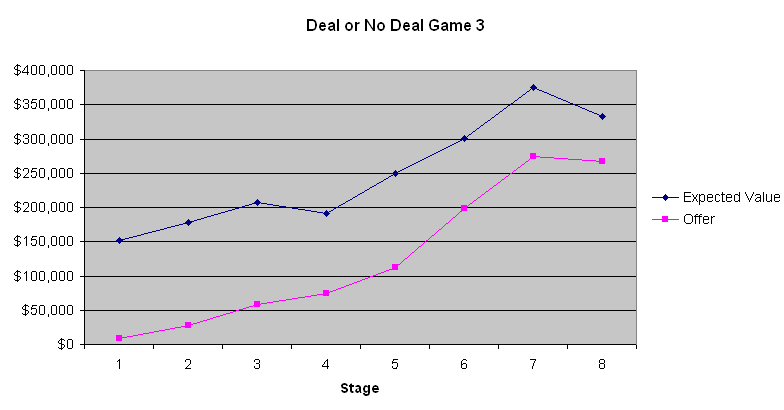
從這三張圖表中,最明顯的一點是,銀行開出的前四到六個出價都很糟糕。平均每個箱子在開箱前有131,477.54美元。第一階段只出價9000到13000美元,只有傻瓜才會這麼做。然而,出價逐漸上升。第二局遊戲顯示,當玩家的預期值相當低時,預期值在遊戲接近尾聲時幾乎與銀行家的出價相同。然而,在第一局和第三局遊戲中,當預期值較高時,銀行家顯然試圖利用大多數人在涉及大額賭注時規避風險的天性。我不知道這是否重要,但第二局的參賽者似乎是一個想要大贏的賭徒。根據主持人透過電話與銀行家溝通的評論,銀行家似乎確實會考慮參賽者的言行舉止。如果我是銀行家,我也會這麼做。
如果玩家既不厭惡風險也不傾向於風險,並且不考慮稅務影響,那麼玩家應該不斷拒絕銀行家的報價,直到其中一個報價超過剩餘行李箱的平均數。對大多數人來說,所得稅法的累進性質有利於接受交易。正如我之前所說,我粗略地說,貨幣的價值與金額的對數成正比。因此,你投入的財富越多,你就越傾向於冒險拒絕銀行家的報價。由於涉及的金額如此之大,沒有一種策略適合所有人。不過,我可以相當肯定地說,玩家應該拒絕前四到六個報價,然後根據具體情況(雙關語)接受其他報價。
我正在看「一擲千金」。我意識到銀行家的「出價」只是箱子剩餘價值除以箱子數量(四捨五入)。這遊戲有什麼策略嗎?還是說「一擲千金」總是可以接受的?這取決於你需要開多少箱子還是其他什麼?
正如我在2005年12月26日的專欄文章中指出的那樣,莊家的出價通常遠低於其餘情況的平均值。然而,假設情況總是如此,那麼每種策略的預期價值都會相同。玩家對每種出價都會無動於衷。
在「一擲千金」遊戲開始時,選中 1,000,000 美元案例的機率是 1/26。在排除 1 以外的所有案例後,我的案例中包含 100 萬美元的機率是多少?是 50-50 還是還是 1/26?
50-50
您在2006年4月5日的專欄文章中寫道,如果「一擲千金」只剩下兩個案子,而百萬美元仍在進行中,那麼我的案子贏得百萬美元的機率是五五開。我不同意。這難道不是蒙提霍爾難題的變種嗎?也就是說,百萬美元在舞台上的可能性比在他自己的案子中更大?
不。很多人跟我爭論這個問題。很多作者聲稱,即使引入額外的訊息,機率也不會改變。所以,如果機率一開始是1/26,那它就必須保持不變。與博彩系統推銷員的說法相反,機率確實會隨著額外資訊的引入而改變。我不想在這裡講授基本的機率知識,但任何一本關於條件機率或貝葉斯定理的大學數學書都應該很好地涵蓋這個主題。
讓我來解釋一下《讓我們做個交易》節目中發生的事情。參賽者會從三道簾子中選出一道。一道簾子裡裝著非常珍貴的獎品,另外兩道簾子裡裝著小獎品。為了方便討論,我們假設一道簾子後面是一輛汽車,另外兩道簾子後面是一隻山羊。那麼蒙蒂總是會,我再說一遍,總是會,打開兩道未被選中的簾子中的一道,露出一隻山羊。經過數百場節目的檢驗,這意味著蒙蒂霍爾(主持人)知道汽車的位置,並故意打開露出山羊的窗簾。顯然,當參賽者選擇自己的簾子時,它露出汽車的機率是1/3,而兩道未被選中的簾子中一道露出汽車的機率是2/3。因此,蒙蒂注定會打開一道未被選中、包含目標的簾子。 「注定」是這裡的關鍵字。因為蒙蒂在這個階段無法打開參賽者的簾子,所以參賽者的簾子露出汽車的機率仍然保持在1/3。未選擇的窗簾露出汽車的機率仍然是2/3,但現在汽車都出現在一個窗簾上了。因此,當一隻山羊被揭開後,玩家的窗簾上有汽車的機率是1/3,而另一個未打開的窗簾上有汽車的機率是2/3,因此換窗簾是一個明智的選擇。
下表列出了所有可能的結果。在玩家選擇汽車窗簾的情況下,我請蒙蒂隨意拉開窗簾。可以看到,不拉開窗簾的獲勝機率為 1/3,而拉開窗簾的獲勝機率為 2/3。
我們做個交易吧
| 玩家 選擇 | 車 | 窗簾 已開啟 | 可能性 | 獲勝者 交換 |
| 1 | 1 | 1 | 0% | 無 |
| 1 | 1 | 2 | 5.56% | 否 |
| 1 | 1 | 3 | 5.56% | 否 |
| 1 | 2 | 1 | 0% | 無 |
| 1 | 2 | 2 | 0% | 無 |
| 1 | 2 | 3 | 11.11% | 是 |
| 1 | 3 | 1 | 0% | 無 |
| 1 | 3 | 2 | 11.11% | 是 |
| 1 | 3 | 3 | 0% | 無 |
| 2 | 1 | 1 | 0% | 無 |
| 2 | 1 | 2 | 0% | 無 |
| 2 | 1 | 3 | 11.11% | 是 |
| 2 | 2 | 1 | 5.56% | 否 |
| 2 | 2 | 2 | 0% | 無 |
| 2 | 2 | 3 | 5.56% | 否 |
| 2 | 3 | 1 | 11.11% | 是 |
| 2 | 3 | 2 | 0% | 無 |
| 2 | 3 | 3 | 0% | 無 |
| 3 | 1 | 1 | 0% | 無 |
| 3 | 1 | 2 | 11.11% | 是 |
| 3 | 1 | 3 | 0% | 無 |
| 3 | 2 | 1 | 11.11% | 是 |
| 3 | 2 | 2 | 0% | 無 |
| 3 | 2 | 3 | 0% | 無 |
| 3 | 3 | 1 | 5.56% | 否 |
| 3 | 3 | 2 | 5.56% | 否 |
| 3 | 3 | 3 | 0% | 無 |
同時,在「一擲千金」遊戲中,一切都沒有註定。假設遊戲中剩餘的金額分別為 0.01 美元、1 美元和 100 萬美元。如果剩下三個箱子,那麼打開的箱子裡有可能包含一百萬美元。下表顯示了剩下三個箱子的可能結果。記住,玩家不能打開自己的箱子。
成交或不成交
| 玩家 選擇 | 百萬美元 | 案件 已開啟 | 可能性 | 獲勝者 交換 |
| 1 | 1 | 1 | 0% | 無 |
| 1 | 1 | 2 | 5.56% | 否 |
| 1 | 1 | 3 | 5.56% | 否 |
| 1 | 2 | 1 | 0% | 無 |
| 1 | 2 | 2 | 5.56% | 絕望 |
| 1 | 2 | 3 | 5.56% | 是 |
| 1 | 3 | 1 | 0% | 無 |
| 1 | 3 | 2 | 5.56% | 是 |
| 1 | 3 | 3 | 5.56% | 絕望 |
| 2 | 1 | 1 | 5.56% | 絕望 |
| 2 | 1 | 2 | 0% | 無 |
| 2 | 1 | 3 | 5.56% | 是 |
| 2 | 2 | 1 | 5.56% | 否 |
| 2 | 2 | 2 | 0% | 無 |
| 2 | 2 | 3 | 5.56% | 否 |
| 2 | 3 | 1 | 5.56% | 是 |
| 2 | 3 | 2 | 0% | 無 |
| 2 | 3 | 3 | 5.56% | 絕望 |
| 3 | 1 | 1 | 5.56% | 絕望 |
| 3 | 1 | 2 | 5.56% | 是 |
| 3 | 1 | 3 | 0% | 無 |
| 3 | 2 | 1 | 5.56% | 是 |
| 3 | 2 | 2 | 5.56% | 絕望 |
| 3 | 2 | 3 | 0% | 無 |
| 3 | 3 | 1 | 5.56% | 否 |
| 3 | 3 | 2 | 5.56% | 否 |
| 3 | 3 | 3 | 0% | 無 |
「一擲千金」表格顯示,如果剩下三個箱子,玩家打開百萬美元箱子的機率是1/3(無望中獎),換人獲勝的機率是1/3,換人輸的機率也是1/3。因此,換人箱子的機率相同。如果只剩下兩個箱子,那麼每個箱子中大獎的機率就是50/50。
又到了「一擲千金」的問題了。假設銀行家和席琳狄翁客串演出之後,你只剩下兩個箱子,50萬美元和100萬美元。我猜銀行家的出價會略低於75萬美元。你會選哪一個?如果剩下的兩個箱子分別是0.01美元和100萬美元呢?我想這完全取決於你是不是賭徒,跟賠率沒什麼關係。我問這個問題的原因是,我想知道是否有人能贏得100萬美元(即使他們選的是那個神奇的箱子)。
當獎金金額足以改變人生時,明智的玩家應該謹慎行事,而不是最大化預期價值。一個好的策略應該是最大化預期幸福感。我認為衡量幸福感的一個好函數是你總財富的對數。假設一個人現有財富為 10 萬美元,面臨 0.01 美元和 100 萬美元兩種情況。選擇「不交易」的預期幸福感為 0.5*log(100,000.01 美元) + 0.5*log(1100,000 美元) = 5.520696。設 b 表示玩家無所謂是否接受的銀行報價。
對數(b)= 5.520696
b = 10 5.520696
b = 331,662.50 美元。
所以這位假設的玩家應該會對銀行出價 331,662.50 美元無動於衷。你投入的資金越少,就越應該謹慎行事。通常在遊戲後期,銀行出價接近預期價值,有時甚至會略高一些。玩家贏得百萬美元的唯一合理情況是,他投入了大量資金,並且/或銀行出價異常低廉。製作人似乎喜歡勤奮的中產階級,所以我們不太可能看到有人在涉及大額資金時如此傲慢。我也從未見過銀行在遊戲後期出價低於預期價值 90% 的金額。我們只有在某個無法停止賭博的墮落賭徒出現時才會看到有人贏得百萬美元。當這種情況發生時,我會支持銀行家。
這是《一擲千金》(Deal or No Deal)的後續報道,我最近才第一次看。你的分析假設莊家不知道箱子裡錢的價值。然而,在我看的節目中,在最後階段,兩位選手都選擇了一個有價值的箱子,並且都獲得了(或者說,由於其中一位已經退出,他們本應獲得)高於預期價值(EV)的賠付。在最極端的情況下,當玩家剩下的兩個金額分別為50萬美元和75萬美元時,他們「本應」獲得68.7萬美元的賠付。對此唯一合理的解釋是,莊家知道玩家箱子的價值,並且提供的賠償是基於此的。
這只是我的一點看法,無需回覆。
謝謝你沒有期待我的回复,但我通常都會回答遊戲節目的問題。節目中每一集都聲稱盒子裡的金額是隨機的,Howie 和銀行家都不知道結果。這在《讓我們做個交易》中從未被提及,但蒙提·霍爾顯然知道結果。我也看過銀行家給出高於預期的最後報價,尤其是金額較大的時候。我堅信,這並不是因為銀行家知道玩家盒子裡有什麼。 20 世紀 50 年代, 《21》等節目被揭露存在操縱,引發了一場巨大的醜聞。沒有任何令人信服的理由為了透過銀行報價攫取一些獎金而毀掉一檔成功的節目和所有遊戲節目的完整性。
我可以提出三種理論來解釋為什麼銀行家有時提供的金額高於其餘案例的平均金額。
- 這部劇試圖將銀行家描繪成在辦公室裡為錢操心的人物。豪伊·曼德爾經常評論銀行家的情緒和語氣。或許,將銀行家描繪成一個規避風險的精打細算者,寧願停損也不願冒險發放巨額獎金,會讓這部劇更具戲劇性。
- 真正的銀行家確實厭惡風險。這有點超出我的專業範圍了,但據我所知,遊戲和真人秀通常由獨立於電視網絡的公司製作。這些規模較小的公司會尋求保險公司的協助,以降低參賽者贏得巨額獎金的風險。在這種情況下,保險公司才是真正的銀行家,並且可能會影響節目中銀行家的行為。承保此類稀奇古怪事件的保險公司規模並不大,在涉及大額金額時可能更傾向於穩健行事。
在您的例子中,銀行家的報價比預期價值高出9.92%。如果銀行家遵循凱利準則,那麼在總資金只有782,008美元的情況下,這樣的報價也不足為奇,這低於最高獎金。任何一家有自尊心的保險公司都不會如此保守。顯然,僅憑這一點不足以證明您例子中的報價是合理的。
- 節目試圖讓參賽者看起來愚蠢又貪婪。像《你比五年級生聰明嗎? 》和《今夜秀》的「亂穿馬路」這樣的節目,如果我們不能從嘲笑那些被瑣事難倒的人中找到一些滿足感,那它們就不可能成功。 《朋友還是敵人》和《最弱環節》這兩檔節目則出色地揭露了人性的貪婪。我必須承認,當參賽者拒絕高於預期的報價,最終接受較低金額時,我感到幸災樂禍。
我傾向於認為原因是這三個原因的綜合,但主要是第三個原因。
如果我的答案到此結束,肯定會有人評論,質疑銀行家是否真的會提出這些假設性報價。言下之意是,這些報價是為了達到戲劇效果而誇大其詞。我記錄了13場比賽的具體情況。其中一場比賽,還剩三個案件(1000美元、5000美元和50000美元),平均價格為18667美元,而最終報價為21000美元,比預期價格高出12.5%。另一場比賽,還剩兩個案件(400美元和750000美元),平均價格為375200美元,最終報價為400000美元,比預期價格高出6.6%。所以,我認為沒有理由質疑這些假設性報價的可靠性。
連結:
一擲千金公式:本頁面展示了基於一擲千金網站上的免費遊戲的用於計算銀行家報價的新舊公式。
在《最後的危險邊緣》中,如果分數如下,站在每個人的角度,你會下多少錢:
玩家A:10,000美元
玩家B:8,000美元
玩家C:3,500美元
首先,我先做一些假設。首先,我假設這三位選手對《最終危險邊緣》中的投注行為一無所知,除了表格中給出的正確機率。其次,我假設了解類別沒有任何幫助。第三,我還假設三位選手都想爭取勝利,不想讓另一位選手打成平手。
讓我們從玩家C開始。他應該預期,如果B猜對了,A可能會下注6001美元,以保持領先於B。然而,如果A猜錯了,他的籌碼就會降到3,999美元。在這種情況下,C需要至少下注500美元,並且猜對了,才能擊敗A。然而,在我看來,如果必須猜對才能贏,不妨下大注。所以,如果我是CI,我會孤注一擲。
B 左右為難,不知道該押大還是押小。小額投注應該不超過 999 美元,這樣才能在 C 正確的情況下保持高於 C 的賠率。小額投注的好處是,無論怎樣,都能保持在 C 之上,希望 A 押大,但結果卻是錯的。大額投注不一定要押全,但也有可能。大額投注的好處是,希望 A 押小,或押大但結果卻是錯的,但兩者都需要 B 正確。
A 基本上想和 B 走同一條路。 A 的小額投注可以是 0 美元到 1000 美元之間的任何金額,如果 B 下注 999 美元,A 的投注額就會高於 B 的投注額。大額投注應該是 6001 美元,這樣既能保證 A 猜對了就能贏,又能在 B 下大注,而其他三位玩家都猜錯的情況下保住勝算。
為了幫助計算正確和錯誤答案的八種可能結果的機率,我查看了 j-archive.com(現已停用)上第 20 季至第 24 季的《危險邊緣》最終結果。結果如下:玩家 A 領先,其次是玩家 B,C 墊底。
《最終危險》的可能結果
| 玩家A | 玩家B | 玩家C | 可能性 |
| 正確的 | 正確的 | 正確的 | 21.09% |
| 正確的 | 正確的 | 錯誤的 | 9.73% |
| 正確的 | 錯誤的 | 正確的 | 10.27% |
| 錯誤的 | 正確的 | 正確的 | 8.74% |
| 正確的 | 錯誤的 | 錯誤的 | 13.33% |
| 錯誤的 | 正確的 | 錯誤的 | 10.27% |
| 錯誤的 | 錯誤的 | 正確的 | 8.63% |
| 錯誤的 | 錯誤的 | 錯誤的 | 17.92% |
使用我在我的網站mathproblems.info上的問題 192 中解釋的博弈論邏輯,我發現 A 和 B 應該如下隨機化他們的策略。
玩家 A 應該下大注的機率為 73.6%,下小注的機率為 26.4%。
玩家 B 應該以 67.3% 的機率下大注,以 32.7% 的機率下小注。
玩家 C 應該以 100.0% 的機率下大賭注。
如果遵循此策略,每位玩家獲勝的機率如下:
玩家A:66.48%
玩家B:27.27%
玩家C:6.25%
順便說一句,根據上表,領先者答對《最終危險邊緣》的機率為 54.4%,第二名玩家為 49.8%,第三名玩家為 48.7%。總體機率為 51.0%。
從實際操作上講,玩家確實了解投注行為。在我看來,玩家下注的次數往往超出了數學上的合理範圍。有趣的是,我發現在“每日雙倍”節目中投注過於保守,超出了數學上的合理範圍。我認為肯詹寧斯之所以表現如此出色,原因之一就是他在“雙倍雙倍”節目中下注激進。總之,如果我真的上節目,我會假設其他兩位玩家也會下注激進。所以我實際的投注金額是:A 下注 6000 美元(對 B 友善),B 下注 0 美元,C 下注 3495 美元(留一點未下注金額,以防 A 愚蠢地押上所有金額或只剩 1 美元,結果錯了)。
在有人向我提問如何在實際場地中抽取隨機數字之前,讓我先建議一下斯坦福·黃 (Stanford Wong) 的策略,即使用手錶的秒針從 1 到 60 中抽取一個隨機數。
一檔名為「金錢本色」的全新遊戲節目在英國首播。節目中,一位參賽者隨機獲得一筆目標金額,據悉金額介於5.5萬英鎊到7.9萬英鎊之間。為了贏錢,參賽者需要從20台提款機中選擇10台,每台提款機的金額從1000英鎊到20000英鎊不等,以1000英鎊為增量遞增。當他選擇一台提款機時,機器會從1000英鎊開始遞增,以1000英鎊為增量遞增。
玩家可以隨時喊“停!”,然後他會將螢幕上顯示的金額存入帳戶。如果玩家沒有及時停止,導致機器的錢用完,則他不會存入任何金額。服務員會提供統計數據,例如剩餘的機器數量、剩餘的贏錢金額、每台機器的平均贏錢金額以及機器中剩餘的金額。
玩家可以“玩空檔”,也就是說,如果連續選中的機器分別為 4000 英鎊、5000 英鎊和 6000 英鎊,那麼一旦其中一台機器的投注額超過 3000 英鎊,就保證能達到 7000 英鎊。我的問題是,玩家應該使用什麼樣的策略?
這種事我得花上幾週時間分析。可惜的是,我幾乎在三個月後才看到你的留言,因為當時積壓了大量「問巫師」的問題。維基百科頁面似乎顯示那部戲劇很失敗,已經被取消了。不過,這仍然引出了一個有趣的問題。
女服務生會很貼心地告訴你每台剩餘機器達到目標所需的平均金額。經過幾個小時的反覆思考,我實在想不出比設定的平均值高出約 25% 的停止目標更好的辦法了。這只是一個有根據的猜測,所以請不要讓我證明它是最優的。正如你所說,也要抓住機會,不要在已經選好的金額之前停下來。
當只剩下兩台機器時,如果所需金額不超過13,000英鎊,我會盡量在倒數第二台機器上全部買入。如果所需金額超過14,000英鎊,我會盡量在下一台機器上買一半。
如果他們真的要重啟這部劇,我希望我的英國讀者能告訴我。這類謎題或許會讓我著迷,就像《永恆謎題》一樣,巧合的是(或許也巧合)它也在英國上映了。
P.S:為什麼在英國,「colour」要用au拼寫?我不明白。
《The Price is Right》中的 Punch a Bunch 遊戲每次出拳的平均獎金和最佳策略是多少?
對於那些不熟悉規則的人,可以在「價格猜猜」網站上查看規則說明。如果您不熟悉這個遊戲,請花點時間去那裡看看,因為我假設您知道規則。 YouTube上也有一些關於這個遊戲的影片。這裡有一個舊視頻,展示了第二次機會,但當時的最高獎金只有1萬美元。現在是2.5萬美元。
首先,我們來計算一下沒有第二次機會的獎金的預期價值。下表顯示,平均為1371.74美元。
打出一堆獎品,沒有第二次機會
| 獎 | 數位 | 可能性 | 預期勝利 |
| 25000 | 1 | 0.021739 | 543.478261 |
| 10000 | 1 | 0.021739 | 217.391304 |
| 5000 | 3 | 0.065217 | 326.086957 |
| 1000 | 5 | 0.108696 | 108.695652 |
| 500 | 9 | 0.195652 | 97.826087 |
| 250 | 9 | 0.195652 | 48.913043 |
| 100 | 9 | 0.195652 | 19.565217 |
| 50 | 9 | 0.195652 | 9.782609 |
| 全部的 | 46 | 1.000000 | 1371.739130 |
其次,計算有第二次機會的平均獎金。下表顯示,平均獎金為225美元。
利用第二次機會贏得豐厚獎金
| 獎 | 數位 | 可能性 | 預期勝利 |
| 500 | 1 | 0.250000 | 125.000000 |
| 250 | 1 | 0.250000 | 62.500000 |
| 100 | 1 | 0.250000 | 25.000000 |
| 50 | 1 | 0.250000 | 12.500000 |
| 全部的 | 4 | 1.000000 | 225.000000 |
第三,根據玩家找到的第二次機會數量來建立預期價值表。這可以透過簡單的數學計算得出。例如,2次第二次機會的機率為(4/50)×(3/49)×(46/48)。 s次機會的預期收益為1371.74美元+s×225美元。下表顯示了0到4次第二次機會的機率和平均收益。
Punch a Bunch 獎品回饋表
| 第二次機會 | 可能性 | 平均勝利 | 預期勝利 |
| 4 | 0.000004 | 2271.739130 | 0.009864 |
| 3 | 0.000200 | 2046.739130 | 0.408815 |
| 2 | 0.004694 | 1821.739130 | 8.551020 |
| 1 | 0.075102 | 1596.739130 | 119.918367 |
| 0 | 0.920000 | 1371.739130 | 1262.000000 |
| 全部的 | 1.000000 | 1390.888067 |
因此,每次出拳的平均贏利(包括第二次機會的額外獎金)為 1390.89 美元。
下表展示了我根據剩餘擊球次數確定最低贏額的策略。請注意,玩家可以透過三次第二次機會贏得 1,000 美元 + 250 美元 + 100 美元 + 50 美元的獎金,最終贏得 1,400 美元。
打擊一堆策略
| 剩餘沖孔數 | 最低站立高度 |
| 3 | 5,000 美元 |
| 2 | 5,000 美元 |
| 1 | 1,400美元 |
這個問題是在我的同伴網站Wizard of Vegas的論壇中提出並討論的。
如果您不確定答案,那麼在遊戲節目《百萬美元大灑千里》中分配資金的最佳策略是什麼?
為了其他讀者的利益,讓我先回顧一下規則。
- 一支球隊的起步資金為 1,000,000 美元。
- 團隊需要回答一道選擇題。
- 團隊要把錢分給所有可能的答案。所有投在正確答案上的錢都會進入下一個問題。
- 團隊必須完全排除至少一個可能的答案,不投入任何資金。
- 這個過程重複幾輪。玩家也有一次改變主意的機會。
顯然,如果團隊確定答案,那麼他應該把所有錢都押在正確答案上。如果團隊能把答案縮小到兩個,但每個答案都有50%的正確機率,那麼他們應該把錢平均分配給這兩個選項。
如果團隊傾向於某個答案,但又不完全排除其他一個或多個答案,情況就會變得更加困難。我們來看一個例子。假設團隊確定每個正確答案的機率如下:A 10%,B 20%,C 30%,D 40%。他們應該如何分配他的錢?
我認為答案是遵循凱利準則。簡而言之,團隊應該在每次提問時最大化其財富對數。要做到這一點,你必須考慮你已經擁有多少財富。
假設您現有的財富(獨立於節目本身累積)為 100,000 美元。這是您的第一個問題,因此您需要分配 1,000,000 美元的遊戲節目獎金。首先,排除機率最低的選項,以符合節目規則。然後,您需要最大化 0.2×log(100,000+b*1,000,000) + 0.3×log(100,000+c*1,000,000) + 0.4×log(100,000+d*1,000,000),其中小寫的比例分別代表每個分配的比例。
這可以用微積分和解三項式方程式、反覆試驗,或者我更喜歡用Excel的「目標搜尋」功能來解答。無論你用什麼方法,正確答案都是B佔18.9%,C佔33.3%,D佔47.8%。
當然,節目裡沒人能在規定時間內完成所有這些數學題,更別提你還得在這段時間內轉移一大堆現金。我更實際的建議是,根據你對答案正確機率的評估來分配資金,假設最不可能的選項不存在。在這個例子中,B選項分配22.2%,C選項分配33.3%,D選項分配44.4%。
這個問題是在我的同伴網站Wizard of Vegas的論壇中提出並討論的。
密西根州彩票有一款三人遊戲,規則如下: 在這場遊戲中,最後出局有什麼位置優勢嗎?每位玩家的最佳策略是什麼? 這裡有一個YouTube視頻,展示了這場遊戲。
首先,最後行動沒有任何位置優勢。由於在前面的玩家進行遊戲時,玩家會被安排在隔音室內,所以順序並不重要。
其次,博弈中必須存在一個納許均衡,其中至少獲得 x 分的策略優於其他任何策略。問題在於找到 x。
我問自己,如果每位玩家拿到的不是1到100的牌,而是0到1之間均勻分佈的隨機數,並尋找一個點x,讓完美的邏輯學家對停牌和換牌無感,那麼策略會是什麼。有了這個答案,我們就能輕易地將答案應用在1到100的離散分佈上。
我就不多說了,讓讀者自己體會這個問題的樂趣吧。請參閱下面的連結以獲取答案和解決方案。
答案為 0 到 1 的連續分佈。
答案為 1 到 100 的離散分佈。
如需了解我的解決方案,請點擊此處(PDF) 。
這個問題是在我的「拉斯維加斯巫師」論壇中提出並討論的。
假設不知道任何東西的價格,那麼《價格猜想》中的競賽遊戲的最佳策略是什麼?
對於不熟悉規則的玩家,玩家會得到四個價格標籤,必須將它們貼在四件物品上。完成後,玩家拉動一個拉桿,拉桿會顯示正確匹配的數量。如果玩家的正確配對次數少於四個,則可以重新排列標籤,然後重試。玩家可以在45秒內嘗試盡可能多的次數。
我的建議是,根據先前的選擇和得分歷史,始終提交有獲勝機會的選擇。如果第一個得分為 0,則不要將兩組標籤顛倒過來,而是將所有內容向任何方向移動一位。
如果你無法當場理解邏輯,下面我會為你詳細說明。若要使用此策略,請為不同的標籤指派字母 A、B、C 和 D。然後按照圖示順序,從左到右將它們放置在舞台上。始終從 ABCD 開始。然後,請查看下面的樂譜歷史記錄,並選擇與該樂譜序列對應的標籤順序。
如果為 0,則 BCDA
如果 0-0,則 CDAB
如果 0-0-0,則 DABC(必須贏)
如果是 0-1,則為 BDAC
如果 0-1-0,則 CADB(必須贏)
如果 0-1-1,則 CDBA
如果 0-1-1-0,則 DCAB(必須贏)
如果 0-2,則 BADC
如果 0-2-0,則 DCBA(必須贏)
如果為 1,則 ACDB
如果 1-0,則 BDCA
如果 1-0-0,則 CABD
如果 1-0-0-1,則 CBAC(必須獲勝)
如果 1-1,則 BDCA
如果 1-1-0,則 CABD
如果 1-1-0-1,則 CBAC(必須獲勝)
如果 1-1-1,則 BCAD(必勝)
如果是 2,那麼 ABDC
如果 2-0,則 BACD(必須贏)
如果 2-1,則 ACBD
如果是 2-1-0,則 DBCA
如果 2-1-1,則 ADCB
如果 2-1-1-0,則 CBAD(必須贏)
下表顯示了每個總圈數的機率。右下角單元格顯示預期圈數為 10/3。
賽車遊戲
| 轉彎 | 組合 | 可能性 | 返回 |
|---|---|---|---|
| 1 | 1 | 0.041667 | 0.041667 |
| 2 | 4 | 0.166667 | 0.333333 |
| 3 | 8 | 0.333333 | 1.000000 |
| 4 | 8 | 0.333333 | 1.333333 |
| 5 | 3 | 0.125000 | 0.625000 |
| 全部的 | 24 | 1.000000 | 3.333333 |
我在Wizard of Vegas論壇上討論過這個問題。
在「價格猜猜猜」節目的 Showcase Showdown 中,任何特定玩家贏得 25,000 美元的機率是多少?
為了向其他讀者解釋一下,讓我先解釋一下你在說什麼。 Showcase Showdown 是遊戲節目《價格猜猜猜》中的一款遊戲。在 Showcase Showdown 中,每個玩家輪流旋轉一個輪盤,該輪盤停在從 0.05 到 1.00 的每個能被 0.05 整除的數額上的機率相等。如果玩家對第一次旋轉不滿意,他們可以再次旋轉,將第二次旋轉加到第一次旋轉上,但是如果超過 1.00,他們將立即被取消資格。如果出現平局,每位玩家將在決勝局獲得一次旋轉機會,最高旋轉次數獲勝。如果再次出現平局,此過程將重複,直到打破平局。
展示賽對決的主要目的是晉級展示賽。不過,參賽者也可以獲得現金獎勵,具體如下:
- 在第一輪中,如果任何玩家獲得總計 1.00 美元,無論是一次總和還是兩次旋轉的總和,他都將贏得 1,000 美元。
- 在第一輪(也是唯一一輪)決勝局中,如果輪盤停在 0.05 美元或 0.15 美元,則玩家將贏得 10,000 美元。
- 在第一輪(也是唯一一輪)決勝局中,如果輪盤停在 1.00 美元,那麼玩家將贏得 25,000 美元。
我在第101欄解釋了Showcase Showdown的最佳策略。假設遵循該策略,下表將解答您的疑問以及其他各種問題。
展示攤牌統計
| 問題 | 回答 |
|---|---|
| 預計首輪獎金 1000 美元的贏家 | 0.253790 |
| 兩人打平的機率 | 0.113854 |
| 三人平局機率 | 0.004787 |
| 預計第二輪獎金 10,000 美元的獲勝者 | 0.024207 |
| 預計第二輪獎金 25,000 美元 | 0.012104 |
| 預計總獎金 | 798.45 美元 |
| 任何特定玩家贏得 1000 美元的機率 | 0.084597 |
| 任何特定玩家贏得 10,000 美元的機率 | 0.008069 |
| 任何特定玩家贏得 25,000 美元的機率 | 0.004035 |
表格的底行顯示,如果您進行 Showcase Showdown,不考慮您的旋轉順序,您贏得 25,000 美元的機會是 0.004035,即 248 分之一。
我在Wizard of Vegas論壇上提出並討論了這個問題。
在遊戲節目《倖存者》中,有兩支隊伍,一支有九名隊員,另一支有六名隊員。之後,他們被隨機分成三支新的隊伍,每隊五人。每支新隊伍由原九人隊伍中的三名成員和原六人隊伍中的兩名成員組成。這種情況發生的機率是多少?
我們將之前的九人隊稱為隊1,將六人隊稱為隊2。從隊1中挑選三名球員,從隊2中挑選兩名球員的方式數為combin(9,3) × combin(6,2) = 1,260。從15名球員中挑選五名球員的方式總數為combin(15,5) = 3,003。因此,第一隊被分成3/2,有利於隊1的機率為1,260/3,003 = 41.96%。
如果發生這種情況,那麼球隊 1 將剩下 6 名球員,球隊 2 將剩下 4 名球員。從球隊 1 中挑選 3 名球員,從球隊 2 中挑選 2 名球員的方式數為 combin(6,3)×combin(4,2) = 120。從剩下的 10 名球員中挑選 5 名球員的方式總數為 combin(10,5) = 252。因此,假設球隊 1 已經按照 3/2 的分配方式分配,那麼球隊 2 被分配 3/2 的機率為 120/252 = 47.62%。
如果前兩支新隊伍的分成比例為 3/2,有利於前一支隊伍 1,那麼最終的隊伍將在剩餘隊伍中以 3/2 的比例分配。
因此,您問題的答案是 41.96% × 47.62% × 100% = 19.98%。
公式:
組合(x,y)=x! /((y!*(xy)!)
x!= 1*2*3*...*x
這個問題是在我的「拉斯維加斯巫師」論壇中提出並討論的。
我認為詹姆斯霍爾扎伊爾在他上一場比賽中故意輸給艾瑪。我的證據是,在那之前他每場比賽都押大注,但突然在對艾瑪的比賽中押小注。我懷疑製作人想讓肯·詹寧斯在亞歷克斯下台後主持節目。如果主持人擁有兩場節目的記錄,並且贏了錢,節目會更有戲劇性。所以,他們花錢雇了詹姆斯來打假球。
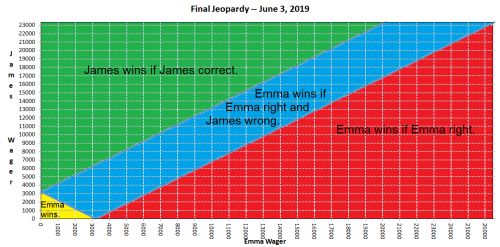
讓我先介紹一下背景。 2019年6月3日,詹姆斯距離打破常規比賽總獎金紀錄僅一步之遙,目前該紀錄仍為2,520,700美元。詹姆斯的場均贏利遠遠超過打破紀錄所需的金額。因此,6月3日,所有人的目光都聚焦在這項紀錄被打破。
而結果卻是,詹姆斯不僅沒能打破紀錄,還輸了。冠軍艾瑪不僅策略性十足,反應靈敏,回答問題也非常準確。她的表現和詹姆斯一如既往。進入《危險邊緣》決賽時,得分如下:
- 艾瑪——26,600美元
- 詹姆斯——23,400美元
- 傑伊——11,000美元
在這種情況下,第二名的獎金超過第一名的一半,而第三名的獎金卻不足一半,通常就取決於第一名和第二名最終的投注金額是高還是低。如果投注金額高,第一名的獎金就足以鎖定勝局。具體來說,投注金額是第二名得分的兩倍減去第一名得分加上一美元。這正是艾瑪投注金額的方式,投注金額為 2×23,400 美元 - 26,600 美元 + 1 美元 = 20,201 美元。大多數情況下,第一名的玩家都會這麼做。
然而,詹姆斯在決定賭注時並不知道艾瑪會怎麼做。下表顯示了根據哪種賭注組合,誰將獲勝。
如果艾瑪下注至少 20,201 美元,那麼如果正確的話,她將鎖定勝利。
如果 Emma 下注較低,那麼如果 (a) James 下注較低或 (b) James 下注較高但錯誤,她將獲勝。
如果詹姆斯下注高,那麼如果 (a) 艾瑪下注高,艾瑪錯了,詹姆斯是對的,或者 (b) 艾瑪下注低,詹姆斯是對的,那麼他就贏了。
如果詹姆斯下注低,而艾瑪下注高並且錯了,那麼他就贏了。
如果玩的是完美邏輯學家,兩人都會隨機做出決定。然而,在這種容易被抓住的情況下,領導者很少會選擇低牌。如果詹姆斯預料到艾瑪會走高牌,那他絕對應該走低牌。這樣,他不用在《危險邊緣》中完全正確就能贏,只需要祈禱艾瑪搞砸了就行了。
如果傑伊全押並且猜對了,那麼詹姆斯的實際出價就是可以覆蓋傑伊的正確金額:23,400 美元 - 2×11,000 美元 - 1 美元 = 1,399 美元,這對於擊敗艾瑪來說是一個低賭注。
如果猜對了,詹姆斯將因獲得第二名而比獲得第三名多獲得 1,000 美元。
總而言之,我完全否認詹姆斯輸掉比賽的陰謀論。他打球的方式是正確的,但輸球的原因既有強大的對手,也有大多數人所說的「運氣不好」。
外部連結
- 《危險邊緣》名人堂
- James Holzhauer 談論《危險邊緣》 ——我在《拉斯維加斯巫師》論壇上的討論。
在《危險邊緣》的「最終挑戰」中,如果第二名玩家的獎金比第一名玩家多出三分之二,那麼最佳策略是什麼?假設第三名玩家不參與遊戲。
首先聲明一下。以下分析基於統計平均值。實際玩家應該根據自己對「最終危險」類別的了解程度以及對手答對的機率進行心理調整。
為了回答你的問題,我首先查看了《危險邊緣》檔案庫中的四個季度的數據,以了解第一名(領先者)和第二名(追趕者)玩家在《危險邊緣》決賽中正確和錯誤表現的四種可能組合。
最終《危險邊緣》記分卡
| 領先球員 | 追逐球員正確 | 追逐球員不正確 | 全部的 |
|---|---|---|---|
| 正確的 | 29.0% | 25.5% | 54.5% |
| 不正確 | 17.7% | 27.8% | 45.5% |
| 全部的 | 46.8% | 53.2% | 100.0% |
在繼續之前,讓我們先定義一些變數:
x = 領先球員得分較高的機率。
y = 追逐球員走高的機率。
f(x,y) = 高玩家獲勝的機率。
讓我們用上表中的 x 和 y 來表示 f(x,y):
f(x,y) = 0.823xy + 0.545x(1-y) + 0.468(1-x)y + (1-x)(1-y)
f(x,y) = 0.810 xy - 0.455x - 0.532y + 1
為了找出 x 和 y 的最佳值,讓我們對 x 和 y 取 f(x,y) 的導數。
f(x,y) d/dx = -0.455 + 0.810y = 0
因此 y = 0.455/0.810 = 0.562
f(x,y) d/dy = -0.532 + 0.810x = 0
因此 x = 0.523/0.810 = 0.657
因此,高玩家下高注的機率為 65.7%,低玩家下高注的機率為 56.2%。
根據觀察,我認為高玩家下注高額的機率超過 65.7%,因此如果我排在第二位,我會下低額賭注。
如果兩個玩家都遵循這種隨機策略,那麼領先玩家獲勝的機率為 70.1%。
撇開所有理論不談,如果你領先,預測追趕者會做什麼,然後照做。如果你追趕,預測領先者會做什麼,然後反其道而行。此策略適用於所有此類錦標賽。這個問題是在我的「拉斯維加斯巫師」論壇中提出並討論的。
在《危險邊緣》一輪開始時,為什麼有些玩家,例如詹姆斯·霍爾茨豪爾,會從最底層開始選?先從最上面的簡單問題熱身不是更合理嗎?部分原因是為了確保玩家對這個類別有充分的理解,因為這些類別有時比較棘手。
原因是每日雙倍獎勵有91.5%的機率被放置在最底下的三行。下表顯示了在13,660個每日雙倍獎勵中,它們在面板上的位置。
每日雙人房位置
| 排 | 第 1 列 | 第 2 列 | 第 3 列 | 第 4 列 | 第 5 列 | 第 6 欄 | |
|---|---|---|---|---|---|---|---|
| 1 | 5 | - | 3 | 3 | 2 | 3 | 16 |
| 2 | 280 | 137 | 216 | 167 | 207 | 140 | 1,147 |
| 3 | 820 | 442 | 677 | 658 | 643 | 472 | 3,712 |
| 4 | 1,095 | 659 | 982 | 907 | 895 | 627 | 5,165 |
| 5 | 787 | 403 | 670 | 671 | 613 | 476 | 3,620 |
| 全部的 | 2,987 | 1,641 | 2,548 | 2,406 | 2,360 | 1,718 | 13,660 |
資料來源: J! 檔案。
這是以每日雙倍在棋盤的每個單元格中出現的頻率的形式呈現的相同數據。
每日雙倍機率
| 排 | 第 1 列 | 第 2 列 | 第 3 列 | 第 4 列 | 第 5 列 | 第 6 欄 | |
|---|---|---|---|---|---|---|---|
| 1 | 0.0% | 0.0% | 0.0% | 0.0% | 0.0% | 0.0% | 0.1% |
| 2 | 2.0% | 1.0% | 1.6% | 1.2% | 1.5% | 1.0% | 8.4% |
| 3 | 6.0% | 3.2% | 5.0% | 4.8% | 4.7% | 3.5% | 27.2% |
| 4 | 8.0% | 4.8% | 7.2% | 6.6% | 6.6% | 4.6% | 37.8% |
| 5 | 5.8% | 3.0% | 4.9% | 4.9% | 4.5% | 3.5% | 26.5% |
| 全部的 | 21.9% | 12.0% | 18.7% | 17.6% | 17.3% | 12.6% | 100.0% |
尋找每日雙倍獎勵的原因是,這是讓你的分數翻倍的好方法。大多數參賽者對任何給定線索的正確率都在 80% 到 90% 左右。如果能押注 80% 到 90% 的勝率,那麼贏得等額的獎金就非常划算了。詹姆斯·霍爾茨豪爾之所以能贏得這麼多獎金,一個主要原因就是他積極地尋找每日雙倍獎勵,而且一旦找到,大多數時候都會「全押」。這也是他輸給艾瑪的原因,艾瑪也用同樣的策略對付他。
假設玩家不知道獎品的價格,那麼在「價格猜猜猜」遊戲中玩競賽遊戲的最佳策略是什麼?
為了讓不熟悉該遊戲的讀者了解一下,這裡有一個該遊戲的影片。
我認為以下策略的平均回合數最低。有很多策略可以與之匹敵,但我認為沒有任何策略能超越它。
若要使用該策略,請將四個價格標籤標記為 1、2、3 和 4。根據您過去正確回答的問題的歷史記錄,從左側的第一個轉彎開始,將它們放在四個獎品上。
競賽遊戲策略
| 歷史 | 一等獎 | 獎品二 | 三等獎 | 獎品 4 |
|---|---|---|---|---|
| 沒有任何 | 1 | 2 | 3 | 4 |
| 0 | 2 | 1 | 4 | 3 |
| 0,0 | 3 | 4 | 2 | 1 |
| 0,0,0 | 4 | 3 | 1 | 2 |
| 0,0,2 | 3 | 4 | 1 | 2 |
| 0,0,2,0 | 4 | 3 | 2 | 1 |
| 0.2 | 2 | 3 | 4 | 1 |
| 0,2,0 | 4 | 1 | 2 | 3 |
| 0,2,1 | 2 | 4 | 1 | 3 |
| 0,2,1,0 | 3 | 1 | 4 | 2 |
| 1 | 1 | 3 | 4 | 2 |
| 1,0 | 2 | 4 | 3 | 1 |
| 1,0,0 | 3 | 1 | 2 | 4 |
| 1,0,0,0 | 4 | 2 | 1 | 3 |
| 1,1 | 1 | 4 | 2 | 3 |
| 1,1,0 | 2 | 3 | 1 | 4 |
| 1,1,0,0 | 3 | 2 | 4 | 1 |
| 1,1,0,0,0 | 4 | 1 | 3 | 2 |
| 2 | 2 | 1 | 3 | 4 |
| 2,0 | 1 | 2 | 4 | 3 |
| 2,1 | 1 | 3 | 2 | 4 |
| 2,1,0 | 4 | 2 | 3 | 1 |
| 2,1,1 | 1 | 4 | 3 | 2 |
| 2,1,1,0 | 3 | 2 | 1 | 4 |
下表顯示了在 24 種可能的排列方式中,四個價格標籤需要 1 到 5 次旋轉的機率。
所需回合數
| 轉彎 | 數位 | 可能性 |
|---|---|---|
| 1 | 1 | 4.17% |
| 2 | 4 | 16.67% |
| 3 | 8 | 33.33% |
| 4 | 9 | 37.50% |
| 5 | 2 | 8.33% |
| 全部的 | 24 | 100.00% |
取點積,該策略下所需的平均轉數為 3.29167。
我在Wizard of Vegas論壇上提出並討論了這個問題。
我聽說了《危險邊緣》的投注規則,叫「三分之二規則」。你知道嗎?
是的。這指的是當第二名玩家的得分超過第一名玩家的2/3時,他的策略就會改變。
讓我們將情況簡化為雙人遊戲,如下所示:
- 狀況A:第二名的人數還不到第一名的一半。
- 情境 B:第二位玩家擁有第一名的 1/2 到 2/3 份額。
- 狀況C:第二名擁有第一名的2/3以上。
在繼續深入討論之前,我想提醒讀者《危險邊緣》規則的一項變化,該規則在「最終危險邊緣」之後對平局進行了修改。現在不再是雙方選手同時晉級,而是設定一個突然死亡決勝題。以下就是這種情況。
情況 A
假設 A=10,000 美元,B=4,000 美元
玩家A不應冒險下注,下注金額不應超過A-2B-1。如果他對該類別沒有信心,可以下注0美元。無論哪種方式,他都能確保獲勝。在這種情況下,A的下注金額應在0美元到1999美元之間。
玩家B毫無希望,除非A下注過多而輸掉比賽。在這種情況下,B應該考慮第三名的分數,並儘量保持領先,如果可以的話,爭取第二名贏得2000美元,而不是第三名贏得1000美元。
情況 B
假設 A=10,000 美元,B=6,000 美元
A 的策略是預期 B 會全押,如果押對了,押注金額會涵蓋 2B。然而,為了安全起見,他不應該押注過高,以免押錯後金額低於 B。在這種情況下,他應該至少押注 2B - A + 1 和 AB - 1。在這種情況下,押注範圍是 2,001 美元到 3,999 美元。
B 的策略是,如果答對了,至少要獲得足夠的分數才能超過 A,並提高總分。在本例中,A 的分數是 4,001 美元,B 的分數是 6,000 美元。
如果兩位玩家都按照預期行事並遵循此策略,那麼玩家 B 獲勝的唯一可能性是 A 猜錯而 B 猜對。這種情況的機率約為 19%。
情況 C
這裡的事情變得更加複雜,涉及更多的博弈論和隨機化。
假設 A=$10,000,B=$7,000。
在進一步探討之前,重要的是估算「最終危險邊緣」線索被正確解答的機率。根據第30至34季的數據,第一名玩家的正確率為52%,第二名玩家的正確率為46%。然而,這些機率是正相關的。以下是所有四種可能性的細分:
- 均正確:27%
- 第一名正確,第二名錯誤:25%
- 第一個位置錯誤,第二個位置正確:19%
- 兩者都不正確,為 29%。
儘管前兩位玩家的 Jeopardy 平均答對率為 49%,但兩人都答對或都答錯的機率卻高達 56%。
當然,這些可以根據類別而改變,但讓我們保持簡單並使用上述機率。
在這種情況下,玩家B不必依賴A錯而B正確。他可以下注較低金額,例如0美元,確保在A錯的情況下獲勝。換句話說,如果A的賭注足以彌補B的賠率(如果正確),那麼如果A錯而B的賭注為0美元,他就有可能跌破B的賠率。
然而,如果A預測B會押低注,例如0美元,那麼A也可以押0美元來鎖定勝局。兩位玩家基本上都可以選擇押低注還是押高注。 A應該希望押與B相同的注,而B應該押與B相反的注。如果兩位玩家都是完美的邏輯學家,他們就會隨機做出決定。
在這種情況下,A 的高額投注應為 2B-A+1 至 AB-1,與情況 B 相同。在這種情況下,A 的低額投注應為 2,999 美元至 4,001 美元。
B 的高額投注應與情況 B 相同,如果正確,投注金額應足以超過 A。在本例中,分別為 3,001 美元和 7,000 美元。 B 的低額投注應為 0 美元。
如果我跳過數學計算並直接討論兩位玩家的隨機化策略,請原諒我。
玩家 A 選擇高牌的機率為 62.3%,選擇低牌的機率為 37.7%。
球員 B 應該處於高位,機率為 61.2%,處於低位,機率為 38.8%。
假設兩位玩家都遵循這種隨機化策略,且機率配對正確,則玩家 A 獲勝的機率為 65.2%。
如果玩家 A 的得分超過玩家 B 的 2/3,那麼他獲勝的機率就會上升到 81.0%。
在雙重危險中下注時,兩位玩家都應該牢記 2/3 規則的重要性。