德州撲克 - 機率論 - 普通
在一場有 10 名玩家玩 50 手牌的德州撲克遊戲中,同一個玩家同時拿到兩張四條和一張同花順的機率是多少?
七張牌中出現四條的機率為 0.00168067,同花順的機率為 0.00027851。設 x 為出現四條的機率,y 為出現同花順的機率,則求出的機率為 combin(50,2)*48*x 2 *y*(1-xy) 47 。答案為 0.0000421845,即 23,705 分之一。
在德州撲克中,拿到同花的機率是多少?玩家在七張牌梭哈和德州撲克中哪個比較容易拿到同花?
你可以參考我關於撲克機率的部分,機率是3.03%。德州撲克和七張牌梭哈的賠率是一樣的。
在德州撲克河牌圈拿到同花大順的機率是多少?
對於那些不知道的讀者來說,河牌是德州撲克中的第五張也是最後一張公共牌。玩家必須在自己的兩張牌和五張公共牌之間組成最好的牌型。所以,你的問題是,玩家用七張牌組成皇家同花順,而第七張牌也屬於皇家同花順的機率是多少。在不考慮牌的情況下,用七張牌組成五張皇家同花順的機率是 4*combin(47,2)/combin(52,7) = 4324/133784560,即 30940 分之一。第七張牌組成皇家同花順的機率是 5/7。所以最終機率是 21620/936491920,即 43316 分之一。
在德州撲克中,從翻牌開始在第五街形成一個間隙或兩個間隙的順子的可能性有多大?
為了方便讀者,我先問一下,如果牌堆裡還剩下47張牌,用另外兩張牌填補順子中間缺口(一或兩張)的機率是多少。如果缺口是1-combin(43,2)/combin(47,2) = 0.164662。若缺口是2張,機率是4 2 /combin(47,2) = 0.0148。
在德州撲克中,如果翻牌都是相同花色,那麼任何給定玩家持有另外兩張相同花色的牌的機率是多少?
剩餘 10 張同花色的牌,牌堆中剩餘 49 張。因此,機率為 combin(9,2)/combin(49,2) = 36/1176 = 0.0306。
德州撲克和七張牌梭哈中各種牌型的機率一樣嗎?還是因為公共牌的不同,它們會有所不同?您能解釋一下為什麼嗎?
是的,機率是一樣的。 52張牌中隨機抽取7張,無論它們是如何從牌堆中抽出的,也無論你和誰分享,抽到的機率都是一樣的。
在最初的兩張牌中,您能告訴我在 35 手牌中獲得 7 手 Ace King 或更好的牌的機率是多少嗎?
拿A/K的機率是(8/52)*(4/51) = 0.012066。拿任一對的機率是(3/51) = 0.058824。因此,拿到一對或更好牌的機率是0.07089。拿到剛好七手A/K或更好牌的機率是combin(35,7)*(.07089)^7*(1-.07089)^28 = 0.00772。要計算7或更大的機率,我們需要逐一計算7到35的點數。總和為0.010366551。
如果您的底牌是同花色的,您如何計算在德州撲克中翻牌時獲得 4 張同花或更好的牌的機率。
再出現兩張同花色牌的機率為 39*combin(11,2)/combin(50,3) = 0.109439。再出現三張同花色牌的機率為 combin(11,3)/combin(50,3) = 0.008418。因此,再出現至少兩張同花色牌的機率為 0.117857。
巫師先生,首先,我要說一下,您的網站太棒了!我已經看了一段時間了。我查了一下撲克問答,沒看到這個。另一個網站聲稱:「在德州撲克中,翻牌前拿到AK,河牌拿到A或K的機率是二分之一(均等)。」這聽起來直觀上太高了。您怎麼看?再次感謝!
也感謝您的讚美。對於不熟悉德州撲克的人來說,這個問題類似於問,如果給玩家一張A和一張K,再加上剩餘50張牌中的五張隨機牌,玩家能配對出K和/或A的機率是多少。其餘50張牌中,有44張既不是K也不是A。從44張牌中抽出任五張牌的方法數為combin(44,5) = 1,086,088。從全部50張牌中抽出任五張牌的方法數為combin(50,5) = 2,118,760。因此,無法配對出A和/或K的機率為1086088/2118760 = 51.26%。因此,您能配對出的機率為1-51.26% = 48.74%。這非常接近二分之一。
在德州撲克中,兩個玩家擁有不同的四條的機率是多少?
兩位玩家一共9張牌,其中必須包含兩張四條和一張單張。組合數為 combin(13,2)*44 = 3432。從52張牌中抽出9張牌的組合數為 combin(52,9) = 3,679,075,400。因此,你拿到正確牌(但順序不一定正確)的機率為 3432/3,679,075,400 = 1/1,071,992。
然而,卡片是 AAAABBBBC,並不代表兩位玩家的四條牌不同。將它們排列成一手五張牌和兩手兩張牌的組合方式共有 9!/(5!*2!*2!) = 756 種。以下是這 9 張牌的可能排列方式。
四條壞牌組合
玩家 1 | 玩家 2 | 翻牌 | 鏡像圖案 | 每個模式的組合 | 總組合數 |
AA | BB | 美國商務諮詢委員會 | 2 | 72 | |
AA | AB | ABBBC | 4 | 四十八 | 192 |
AA | AA | BBBBC | 2 | 6 | 12 |
AA | 交流電 | ABBB | 4 | 12 | 四十八 |
AA | 西元前 | 支氣管擴張症候群 | 4 | 24 | 96 |
AB | AB | 美國商務諮詢委員會 | 1 | 144 | 144 |
AB | 交流電 | 支氣管擴張症候群 | 4 | 四十八 | 192 |
其中只有第一組和第五組牌的結果會讓兩位玩家拿到不同的四條。因此,AAAABBBBC 組合牌出現兩張不同的四條的機率為 168/756 = 22.22%。
所以你問題的答案是 (3432/3,679,075,400)*(168/756) = 4,823,963 分之一。更實際的說,派對撲克 (Party Poker) 的輸牌手牌是四個 8,就會有一個爆冷大獎 (bad beat jackpot)。假設有兩張四條,兩張都是 8 或更大的機率是 combin(7,2)/combin(13,2) = 21/78 = 26.92%。所以,兩位玩家中任一手牌贏得這個爆冷大獎的機率是 17,917,577 分之一。
昨晚,一位玩家在德州撲克遊戲中向我提出了附加賭注。他說翻牌圈至少會出現一張人頭牌(或任三張點數),並提出等額投注。我應該接受這個賭注嗎?
從40張非人頭牌中抽出3張的方式數為(40*39*38)/(1*2*3) = 9880。從52張非人頭牌中抽出3張的方式數為(52*51*50)/(1*2*3) = 22100。因此,抽不到人頭牌的機率為9880/22100 = 44.71%。因此,抽到人頭牌的機率為55.29%。他這邊的賭注優勢為10.58%。
假設10人玩德州撲克,使用標準的52張牌。每位玩家發完前兩張牌後,「翻牌」(接下來的三張牌)全部是同花色的機率是多少?如果我手中的牌是同花色,或是每張牌都是不同花色,會有什麼不同嗎?
在考慮自己的牌之前,機率是 4× combin (13,3)/combin(52,3) = 5.1764706%。
換個角度來看,翻牌圈第二張牌與第一張同花色牌相符的機率是 (12/51)。翻牌圈第三張牌與第一張同花色牌相符的機率是 (11/50)。 (12/51)×(11/50)=5.1764706%。
如果你考慮自己的牌,賠率會略有變化。如果你有兩張同花色的牌,那麼翻牌圈出現同花色的機率為 pr(同花色同花) + pr(不同花色同花) = combin(11,3)/combin(50,3) + 3×combin(13,3)/combin(50,3) = 5.2193878%。
如果您有兩張不同花色的牌,那麼翻牌成同花的機率為 pr(同花色)+ pr(不同花色的同花)= 2×combin(12,3)/combin(50,3)+ 2×combin(13,3)/combin(50,3)= 5.1632653%。
親愛的奇才,真希望我有你的腦袋。無論如何,我和統計學的鬥爭還在繼續。我正在努力想出一個公式,用來計算翻牌圈、轉牌圈和河牌圈(德州撲克)拿到同花的機率,以及我的底牌是否同花。我試過 C(50,2) / C(47,5),但河牌圈拿到同花對子卻不行…我上學的時候應該多加註意!謝謝!你是我最大的粉絲
謝謝你的讚美,但我沒那麼聰明。幾年前我參加了門薩入學考試,但沒能達到要求的前2%。他們拒絕告訴我我的成績有多好,我至今仍感到很沮喪。 1月13日,《危險邊緣》選拔賽將在拉斯維加斯舉行,我已經預約了,但肯定也會搞砸。總之,為了回答你的問題,你現在說:
持有同花底牌:
翻牌後同花:組合(11,3)/組合(50,3)= 165/19600 = 0.842%。
轉牌後同花:(combin(11,2)*39/combin(50,3))*(9/47) = 2.096%。
河牌後沖洗:(combin(11,2)*combin(39,2)/combin(50,4))*(9/46) = 3.462%。
持有非同花底牌:
翻牌後同花:0%
轉牌後同花:2*combin(12,4)/combin(50,4) = 0.430%。
河牌後同花:(2*combin(12,3)*39/combin(50,4))*(9/46) = 1.458%。
這是累積機率。
持有同花底牌:
翻牌同花:0.842%。
轉牌同花:2.937%。
河牌同花:6.400%。
持有非同花底牌:
翻牌圈同花:0.000%
輪流同花:0.430%。
河牌同花:1.888%。
你好,巫師,首先我想說,我很喜歡你給的精準、沒有空話的答案。話說回來,如果德州撲克的底牌是AA,翻牌是KQ9,那麼湊成葫蘆的機率是多少?我琢磨了好久 :( ,還是沒找到一個可靠的答案。
你可以用一張 A 和一張 K、Q 或 9 湊成葫蘆。剩下 2 張 A,還有 3 張 K、Q 和 9。所以這樣的組合共有 2*3*3=18 種。唯一的另一種可能性是 K、Q 或 9 對。這樣的組合共有 3*combin(3,2)=9 種。所有組合數為 47*46/2 = 1081。所以機率為 (18+9)/1081 = 2.50%。
多年來我一直是你的忠實粉絲(甚至在你對撲克和體育博彩感興趣之前),並且期待著你的每一篇「問巫師」專欄。很高興看到你又回來了!我的問題是:在我當地的撲克室,他們會在特定時段提供「Aces Cracked, Win A Rack」活動。也就是說,如果你在他們3-6或4-8的德州撲克遊戲中拿到底牌A,並且輸掉了底池,賭場會給你一架籌碼(100美元)。我想知道a)我拿到底牌A的頻率是多少;b)如果我像我應該的那樣積極地玩,他們會輸掉多少次;c)是不是最好一直過牌,希望輸掉,因為100美元通常比底池的金額要好。如果你能提供任何數據,那就太好了,永遠感激不盡!再次感謝,繼續為大眾提供啟發!
謝謝你的讚美。你在任何一手牌拿到底牌 A 的機率是 6/1326,也就是每 221 手牌一次。根據我的十人德州撲克部分 (/games/texas-hold-em/10players.html),假設所有玩家都堅持到最後,用底牌 A 獲勝的機率是 31.36%。但這只是一個假設。如果非要我猜的話,我估計在真正的十人遊戲中用 A 獲勝的機率大約是 70%。所以拿到底牌 A 然後輸掉的機率是 0.3*(1/221) = 0.1357%。所以,以每次 100 美元計算,每手牌損失 13.57 美分。超過 10 人,撲克室平均每手牌損失 1.36 美元,這會大幅降低抽水。我傾向於同意你的跟注策略,這會讓更多玩家留在牌局中,並增加你輸錢的幾率。
首先,我要感謝你們提供這麼棒的網站。現在我的問題是:我們正在玩德州撲克,翻牌圈用兩張小牌組成了同花聽牌。我們都知道擊中同花的機率,但我們真正想知道的是贏牌的機率。假設我們確定有人的同花牌比我們大。那麼我的問題是,如果只亮出一張同花牌而不是兩張,那麼亮出的機率是多少?此致
不用客氣。所以翻牌後,你拿到了四張同花,牌面上還有兩張。拿到所需花色的機率是 9*38/ combin (47,2) = 342/1081 = 31.64%。
在德州撲克遊戲中,當河牌圈剛好有三張同花的公共牌時,我想知道另一位玩家拿到兩張同花牌,組成比我更大的同花的機率。例如,如果我拿到黑桃89,公共牌包括黑桃3、黑桃7和黑桃K,那麼牌堆裡有4張黑桃比我的9大(TJQA)。假設是9人遊戲,那麼有人拿到兩張黑桃,其中至少有一張更大的黑桃,這種機率是多少?如果只有2張(或3張或x張)黑桃比我最大的底牌大呢?感謝您的幫助和這個很棒的網站。
下表顯示了1至8個高段位玩家和2至10個玩家(包括你自己)的機率。以你舉的這個例子,高段位玩家4個,總共9個玩家,機率為16.45%。我計算這些機率時假設了牌局之間的獨立性,雖然這不是一個正確的假設,但結果應該是一個接近的估計值。
較高同花的機率較高排名(向下)以玩家總數(橫向)巫師估計
| 更高等級 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 1 | 0.71% | 1.41% | 2.11% | 2.80% | 3.49% | 4.17% | 4.85% | 5.52% | 6.19% |
| 2 | 1.31% | 2.61% | 3.89% | 5.15% | 6.40% | 7.62% | 8.84% | 10.03% | 11.22% |
| 3 | 1.82% | 3.60% | 5.36% | 7.08% | 8.77% | 10.43% | 12.05% | 13.65% | 15.22% |
| 4 | 2.22% | 4.40% | 6.52% | 8.60% | 10.63% | 12.61% | 14.56% | 16.45% | 18.31% |
| 5 | 2.53% | 4.99% | 7.39% | 9.72% | 12.00% | 14.23% | 16.39% | 18.50% | 20.56% |
| 6 | 2.73% | 5.38% | 7.96% | 10.47% | 12.91% | 15.29% | 17.60% | 19.85% | 22.03% |
| 7 | 2.83% | 5.58% | 8.25% | 10.84% | 13.36% | 15.81% | 18.20% | 20.51% | 22.76% |
| 8 | 2.83% | 5.58% | 8.25% | 10.84% | 13.36% | 15.81% | 18.20% | 20.51% | 22.76% |
較高同花順的機率依玩家總數(橫向)排名較高(向下)Miplet 模擬
| 更高等級 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 1 | 0.69% | 1.41% | 2.12% | 2.83% | 3.54% | 4.25% | 4.96% | 5.66% | 6.36% |
| 2 | 1.28% | 2.60% | 3.91% | 5.21% | 6.48% | 7.77% | 9.05% | 10.31% | 11.56% |
| 3 | 1.79% | 3.61% | 5.41% | 7.19% | 8.92% | 10.68% | 12.41% | 14.11% | 15.79% |
| 4 | 2.19% | 4.40% | 6.58% | 8.75% | 10.85% | 12.94% | 15.01% | 17.04% | 19.04% |
| 5 | 2.50% | 5.00% | 7.47% | 9.92% | 12.28% | 14.63% | 16.94% | 19.21% | 21.43% |
| 6 | 2.71% | 5.40% | 8.06% | 10.69% | 13.23% | 15.74% | 18.23% | 20.65% | 23.03% |
| 7 | 2.81% | 5.61% | 8.36% | 11.08% | 13.70% | 16.30% | 18.86% | 21.37% | 23.82% |
| 8 | 2.81% | 5.61% | 8.36% | 11.08% | 13.70% | 16.30% | 18.86% | 21.37% | 23.82% |
很棒的網站。我只是想了解一下個人情況。我當時正在玩一場四人德州撲克。我拿到了底牌A。河牌圈我拿到了同花大順。我想知道一開始就拿到A,在河牌圈拿到同花大順的機率是多少?
謝謝。假設皇家牌由你的兩張A中的一張組成,那麼在河牌圈組成皇家牌的機率是2*46=92。這包括你底牌A的兩種花色以及額外牌的46種可能性。從50張牌中發出5張牌,一共有(50,5) = 2,118,760種組合方式。所以機率是92/2,118,760 = 23,030分之一。
如果翻牌圈出現三張相同花色的牌,而我沒有與翻牌圈花色匹配的牌,並且牌桌上還剩下十名玩家,那麼有人拿到同花的機率是多少?
任何一位玩家拿到同花的機率是combin (11,2)/combin(49,2) = 55/1176 = 4.68%。假設每手牌之間相互獨立(但事實並非如此),那麼9位玩家沒有拿到同花的機率是 (1 − 0.0468%) 9 = 64.98%。因此,至少有一位玩家拿到同花的機率是 1-0.6498 = 35.02%。這只是一個快速估算。如果我進行隨機模擬,我認為機率會略高一些,因為每手牌之間相互依賴。
親愛的巫師先生,我最近一直在計算德州撲克中,如果拿到兩張同花的底牌,拿到同花的機率是多少?我的答案一直是5.8%,但這似乎最終是錯誤的,非常感謝您的幫助。
同花,即有三張牌與你的底牌花色相同,其機率為: combin (11,3)×combin(39,2)/combin(50,5) = 122265/2598960 = 0.057706。同花,即有另外四張牌與你的底牌花色相同,其機率為:combin(11,4)×combin(39,1)/combin(50,5) = 2145/2118760 = 0.001012。同花,即有另外五張牌與你的底牌花色相同,其機率為:combin(11,5)/combin(50,5) = 462/2118760 = 0.000218。在公共牌上完成其他花色同花的機率是 3×combin(13,5)/combin(50,5) = 3861/2118760 = 0.001822。將這些數字相加,可得出 0.057706 + 0.001012 + 0.000218 + 0.001822 = 0.060759。
在德州撲克中,出現「破牌」的機率是多少?也就是說,公牌上五張牌既沒有對子,也沒有同花,也沒有順子。
棋盤上五個不同等級的組合數為combin (13,5)*4 5 = 1287 × 1024 = 1,317,888。
這五個點數代表三種花色、兩種花色中的兩種以及一種花色中的一種的機率為 combin(4,2)*2*combin(5,2)*combin(3,2)=360。 Combin(4,2) 表示對於出現兩次的花色,從四種花色中選出兩種的方式數。 2 表示對於出現一次的花色,從兩種方式中選出兩種的方式數。 Combin(5,2) 表示對於兩張牌中的第一種花色,從五種花色中選出兩種的方式數。 4 5表示另外兩種花色,從剩下的三種花色中選出兩種的方式數。
這五個點數代表四種花色、兩種花色中的一種以及一種花色中的三種的機率是 4*combin(5,2)*3*2=240。4 表示對於出現兩次的花色,從四種花色中選出一種花色的方式數。 Combin(5,2) 表示對於該花色的兩張牌,從五種花色中選出兩種的方式數。 3 表示第一種花色,從剩下的三種花色中選出一種的方式數。 2 表示對於第二種花色,從兩種花色中選出一種的方式數。
將四種花色的牌排列在五個不同的等級上,共有 4 5 =1024 種方法。
因此,出現不超過兩張相同花色的牌的機率為 (360+240)/1024 = 600/1024 = 58.59%。
從 13 個等級中排列出 5 個等級,總共有 (13,5)=1287 種組合方式。其中沒有三個等級在 5 的範圍內的組合數量是 79。這個問題沒有簡單的公式。我不得不循環遍歷所有組合。因此,等級之間足夠間隔的機率是 79/1287 = 6.14%。
因此,破損板的機率為 (1317888/2596960)*(600/1024)*(79/1287) = 1.825211%。
我被質疑破發順子的數量。以下是所有79個可能的破發順子的清單。
| 2378Q 2378千 2379Q 2379千 237TQ 237TK 237JQ 237JK 237QK 2389千 238TK 238JK 238QK 2479Q 2479千 247TQ 247TK 247JQ 247JK 247QK | 2489千 248TK 248JK 248QK 257TQ 257TK 257JQ 257JK 257QK 258TK 258JK 258QK 267JQ 267JK 267JA 267QK 267QA 267KA 268JK 268JA | 268QK 268QA 268KA 269JA 269QA 269KA 278QK 278QA 278KA 279QA 279KA 289KA 3489千 348TK 348JK 348QK 358TK 358JK 358QK 368JK | 368JA 368QK 368QA 368KA 369JA 369QA 369KA 378QK 378QA 378KA 379QA 379KA 389KA 469JA 469QA 469KA 479QA 479KA 489KA |
我在印第安納州凱撒賭場玩德州撲克。他們有一個「爆冷大獎」(Bad Beat Jackpot),現在四張或更好的牌會被爆冷。兩位玩家都必須打出兩張底牌,並且必須有四位玩家拿到牌。我的問題是,假設所有玩家都堅持到最後,任何一手牌成為爆冷牌的機率是多少?
我的新Bad Beat Jackpot 部分顯示,在 10 人遊戲中出現這種 bad beat 的機率為 0.0000108,即大約 93,000 分之一。
在您的終極德州撲克回報表中,為什麼對於表中列出的預期回報為負的兩張牌,建議大幅加註?例如同花K/2。
根據我的雙人德州撲克機率,同花 K/2 的可能結果如下:
勝率 51.24%
損失44.82%
抽獎 3.94%
我的終極德州撲克賭桌顯示,玩家在「玩牌」投注上佔有優勢,但在「底注」和「盲注」投注上處於劣勢。在這種情況下,玩家的「底注」和「盲注」投注賠率很低。然而,他在「玩牌」投注上的賠率很有利。因此,透過最大限度加註,他可以從超過50%的勝率中獲得最大價值。其他兩個投注的低賠率使總價值低於50%。如果加註幅度較小,這個價值會更低。
在2008年世界撲克大賽中,萬淵元之的四A被賈斯汀·菲利普的皇家同花順擊敗。我有一個關於這種情況發生的機率的簡單問題。 ESPN和其他媒體稱,發生這種情況的機率約為27億分之一。在我看來,他們只是把公佈的四A出現的機率乘以皇家同花順出現的機率。這是正確的計算方法嗎?
我也不同意27億分之一這個數字。正如你所說,他們似乎獨立計算了每個玩家的機率,只針對兩個玩家都使用底牌的情況,然後相乘。用這種方法,我得到的機率是0.000000000341101,大約是29億分之一。也許27億分之一這個機率也涉及到兩個玩家機率的捨入誤差。他們顯然也忘了把機率乘以2,原因我稍後會解釋。
四張 A 輸給同花大順有以下三種可能情況。
情況 1:一名玩家有兩張同花大順,另一名玩家有兩張 A,並且牌面上有另外兩張 A、另外兩張同花大順牌以及任何其他牌。
例子:
玩家 1:

玩家 2:

木板: 




在大多數撲克室裡,要贏得爆冷大獎,贏家和輸家都必須用掉兩張底牌。影片裡的爆冷也屬於這種類型;事實上,這些牌型也正是爆冷的。
情境 2:一位玩家有兩張同花大順 (TK),另一位玩家有一張 A 和一張「空白」牌,並且牌面上有另外三張 A 和另外兩張同花大順牌。
例子:
玩家 1:

玩家 2:

木板: 




情境 3:一位玩家有一張同花大順 (TK) 和一張空白牌,另一位玩家有兩張 A,並且牌面上有另外兩張 A 和另外三張同花大順的牌。
例子:
玩家 1:

玩家 2:

木板: 




下表顯示了玩家和棋盤每種情況的組合數。右下角單元格顯示組合總數為 16,896。
壞節拍組合
| 案件 | 玩家 1 | 玩家 2 | 木板 | 產品 |
|---|---|---|---|---|
| 1 | 24 | 3 | 四十四 | 3,168 |
| 2 | 24 | 132 | 1 | 3,168 |
| 3 | 704 | 3 | 1 | 2,112 |
| 全部的 | 8,448 |
然而,即使我們把兩位玩家的牌都反過來,仍然可能出現爆牌。所以,我們應該將組合數乘以2。調整後,總有效組合數為2 × 8,448 = 16,896。
雙人德州撲克所有組合的總數為( 52,2) × (50,2) × (48,5) = 2,781,381,002,400。因此,四張 A 輸給同花大順的機率為 8,448/2,781,381,002,400 = 0.0000000060747,約為 1.65 億分之一。單次爆冷的機率為 4.39 億分之一。賠率沒有影片中報道的那麼低,原因很簡單,因為兩手牌有重疊,共用一張 A。換句話說,這兩個事件呈正相關。
根據《揭露紐約視訊撲克的真相》一文,您說得完全正確。玩家的結果確實是命中註定的。無論玩家持有什麼牌,都無法逃脫命運的安排。如果玩家試圖故意逃避命運,遊戲會使用守護天使功能來修正玩家的錯誤。我完全同意作者的觀點,這類遊戲應該警告玩家,他們玩的不是真正的視訊撲克,賠率表只是玩家實際賠率的無意義衡量標準。另外,也要注意的是,這類假視訊撲克機並非紐約獨有。
您好,我是來自夏威夷的七年級學生。我正在做一個關於撲克和洗牌的科學展覽專案。我正在使用您製作的圖表,該圖表是根據遊戲中的玩家人數來計算底牌德州撲克牌型的勝率。希望您能回答幾個問題,幫助我完成我的專案:
- 您是如何得出圖表中的百分比的?
- 如果您使用了電腦程序,您是如何開發它的,花了多長時間?
- 您說過,您創建「機率魔法師」是出於愛好。隨著您的網站越來越出名,您的實驗方式有沒有改變?為什麼?
- 兩人桌的牌局是用一個強力循環程序完成的,它循環了所有1225張可能的對手牌和1,712,304張可能的公共牌。對於三到八名玩家來說,循環會耗費大量的時間,所以我做了一個隨機模擬。
- 我幾乎所有的程式都是用 C++ 寫的,包括我剛才提到的兩個程式。其餘的都是用 Java 或 PERL 寫的。我大部分的程式碼都是從其他撲克程式複製貼上過來的。新程式碼看起來只需要一天就能寫完。
- 是的,我於1997年6月出於愛好創建了我的網站。直到2000年1月,我才開始接受廣告,並嘗試將其發展成一門生意。多年來,它經歷了三個不同的域名。這是它在1999年5月的樣子。網站的宗旨始終如一,即提供基於數學的賭博策略資源。這些年來,我一直在不斷添加更多遊戲和素材。我曾經嘗試過提供2005賽季的NFL選秀信息,但最終以失敗告終。
你好,巫師。我看了你的德州撲克問題,發現你計算出,當你手裡拿著底牌Q時,在牌面上看到A或K的機率是59.85%。你是怎麼得出這個數字的?
一副牌中剩餘的50張牌,五張牌的組合數共有(50,5)=2,118,760種。其中42張牌是2-Q。 42張牌中五張牌的組合數為(42,5)=850,668種。因此,沒有拿到K或A的機率為850,668/2,118,760 = 40.15%。因此,至少拿到一張A或K的機率為1-40.15% = 59.85%。
另一種計算方法是 1 - pr(翻牌中第一張牌不是 A 或 K) × pr(翻牌中第二張牌不是 A 或 K) × pr(翻牌中第三張牌不是 A 或 K) × pr(翻牌中第四張牌不是 A 或 K) × pr(翻牌中第五張牌不是 A 或 K) = 1 × (42/50) × (42/50) × (9419) = 1 × (42/50) × (38/46) = 59.85%。
在德州撲克中,如果我手上有兩張同花色的牌,那麼我在翻牌時再次拿到兩張相同花色的牌的機率是多少?
再湊成兩張同花色的牌,組合數有 (11,2)=55 種,湊成一張不同花色的牌則有 39 種。翻牌圈的牌型組合共有 (50,3)=19,600 種。因此,翻牌圈湊成同花的四張牌的機率為 55×39/19,600 = 10.94%。
我參加了一局線上撲克遊戲,想知道發生這種情況的幾率,請問:
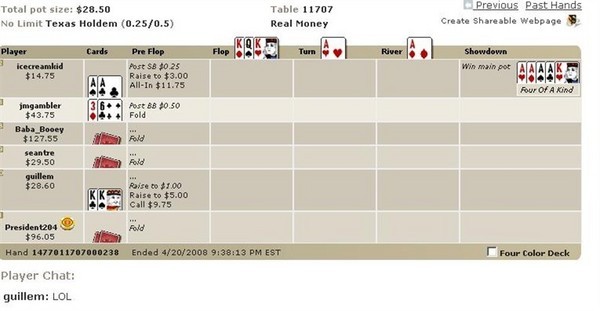
通常情況下,我厭倦了關於爆冷門(bad beat)的問題,但這題實在太難了,我實在無法忽視。在一場雙人遊戲中,如果雙方都有底牌對子,那麼在第一張牌發出之前,四張K被四張A擊敗的機率是 2 * combin (4,2) * combin (4,2) * 44 / ( combin (52,2) * combin (50,2) * combin (48,51) = 262, 130 * 136 1225 * 1712304) = 877,961,175 分之一。這是一場六人遊戲,所以共有 combin (6,2) = 15 種不同的玩家對子。在六人遊戲中,這個機率要高出 15 倍,即 58,530,745 分之一。發出所示底牌後,翻牌前,該手牌以原樣結束的機率為 38,916 分之一。
拉斯維加斯一家牌室正在推出一項促銷活動:湊齊四種花色的同花,即可贏得400美元。你必須用兩張底牌,並且有五小時的限時時間。假設每小時35手牌,時鐘從第一次同花開始計時,那麼在五小時內湊齊另外三次同花的機率是多少?謝謝。
假設你的第一手同花是黑桃。每小時35手,五小時內可以玩175手。那你就有175手牌來組成紅桃、方塊和梅花的同花。我假設玩家永遠不會放棄任何有可能組成他需要的花色之一的同花的牌。
使用兩張底牌湊成特定花色(如紅桃)的同花的機率為:combin(13,2)×[combin(11,3)×combin(39,2) + combin(11,4)×39 + combin(11,5)]/(combin(52,2)×combin(50,5))) 10576566/2809475760=0.003764605。在接下來的175手牌中,湊不成紅桃同花的機率為 (1-0.003764605) 175 =0.51682599。
假設其他三張牌湊不齊的機率為pr(無紅桃同花)+pr(無方塊同花)+pr(無梅花同花)是不正確的,因為你會重複計算湊不齊其中兩張牌的機率。所以你應該加上pr(無紅桃或方塊同花)+pr(無紅桃或梅花同花)+pr(無梅花或方塊同花)。然而,這會錯誤地多減未能湊齊所有三張牌的機率。所以你應該加上pr(無梅花、方塊或紅桃同花)。
進行 175 手牌並且從未獲得任何兩張特定花色的機率是 (1-2×0.003764605) 175 =0.266442448。
進行 175 手牌並且永遠無法獲得剩餘三種花色的機率是 (1-3×0.003764605) 175 =0.137015266。
所以答案是 1-3×0.51682599 + 3×0.266442448 - 0.137015266 = 0.111834108。
非常感謝dwheatley對這個問題的幫助。這個問題在我的「Wizard of Vegas 」論壇上討論過。
多伊爾·布倫森(Doyle Brunson)在1976年和1977年兩度贏得世界撲克錦標賽主賽事冠軍。他每次都拿著10-2的底牌,並且兩次都在河牌圈拿到了葫蘆。這到底有多大的機率呢?
給定兩張不同點數的牌,湊成葫蘆的機率是1/121.6。河牌湊成葫蘆的機率是1/207。
在兩次河牌圈拿到這種牌的機率是 43,006 分之一。
如果起始牌是相同的兩張牌(僅在等級上),則發生這種情況的機率為 3,564,161 分之一。
兩次恰好出現 10-2 的機率是 295,379,826 分之一。
剛從退伍軍人協會的撲克之夜回來。連續三次拿到6-6!以前從未發生過這種情況。一個晚上連續三次拿到同點數的口袋對的機率是多少?你可以假設一個晚上總共有120輪。
答案和解決方案出現在以下劇透標籤中。
[/spoiler]在任何給定時間,您可能處於四種狀態:
- 狀態 1:第一手牌或最後一手牌不是口袋對的任何一手牌。
- 狀態 2:最後一手牌是一對底牌。
- 狀態 3:最後兩手牌是相同的底牌對。
- 狀態 4:已經連續出現三個相同的口袋對。
如果你處於狀態 1,那麼你進入狀態 2 的機率是 3/51。否則,你仍處於狀態 1。
如果你處於狀態 2,那麼你可以以 (4/52)×(3/51) 的機率進入狀態 3。否則,你將返回狀態 1。
如果你處於狀態 3,那麼你可以以 (4/52)×(3/51) 的機率進入狀態 4。否則,你將回到狀態 1。
如果您處於狀態 4,則您留在那裡。
也就是說,您可以如下建立轉換矩陣 T:
| 0.941176 | 0.058824 | 0.000000 | 0.000000 |
| 0.941176 | 0.054299 | 0.004525 | 0.000000 |
| 0.941176 | 0.054299 | 0.000000 | 0.004525 |
| 0.000000 | 0.000000 | 0.000000 | 1.000000 |
總共玩了 120 手牌,因此求出 T^120。
| 0.941044 | 0.058549 | 0.000265 | 0.000141 |
| 0.941025 | 0.058548 | 0.000265 | 0.000162 |
| 0.936786 | 0.058284 | 0.000264 | 0.004666 |
| 0.000000 | 0.000000 | 0.000000 | 1.000000 |
右上角的單元格向我們展示了從狀態 1 開始,在三手序列中經過 120 手起手牌後進入狀態 4 的機率,即 0.000141471。
取該數字的倒數,機率是 7068.605131 分之一。
[/spoiler]這個問題是在我的「拉斯維加斯巫師」論壇中提出並討論的。
在電影《皇家賭場》中,在撲克錦標賽的最後一手牌中,四名玩家的牌型如下:
- 沖洗
- 客滿
- 滿堂紅(與第一個不同)
- 同花順
這種情況的機率有多大?
我不得不為此進行模擬。在我的模擬中,我假設沒有人會棄牌。在近22億輪的模擬中,這種情況發生了312次。這相當於大約七百萬分之一的機率。


