輪盤賭 - 常問問題
如果你這樣玩輪盤賭——在0和00各下注5美元,在兩個列各下注15美元。這樣你不是有大約70%的勝率嗎?
你將有2/38的機率贏得140美元,24/38的機率贏得5美元,以及12/38的機率損失40美元。總體期望回報為[(2/38)*140 + (24/38)*5 + (12/38)*-40]/40 = -5.26%。這與雙零輪盤中每次投注的莊家優勢相同(除了0-00-1-2-3組合,其莊家優勢為7.89%)。
假設我走進一家賭場,在輪盤賭的賠率2-1中押注兩個,例如押1-12的100美元,押13-24的100美元。如果是一次性交易,我贏100美元的機率不是63%嗎?我不是說長期來看,只是一次性的賭注。
你說得對,中獎機率是24/38,也就是大約63%。然而,你得冒200美元的風險,才能贏100美元。如果你想進一步提高中獎機率,那就押注任意35個號碼。中獎機率將達到92%。
輪盤賭中有沒有組合投注來最大化賠率的方法?例如,12 的賠率為 2 比 1。如果我下注 22,例如第一組和第二組都是 12,那麼我有 63.16% 的機率贏錢。這比簡單的紅/黑、單/偶或高/低投注要好。雖然我實際上的賠率只有 1 比 1,而不是 2 比 1(如果我贏了,因為中獎號碼不能同時出現在第一組和第二組 12 中,所以我的部分投注必須輸掉),但通過組合兩個投注,賠率略微對我有利。這類組合的賠率已經確定了嗎?如果已經確定了,我可以在哪裡找到它們?
只要你避開0-0-0-1-2-3的組合,任何投注組合的賭場優勢始終是1/19,即5.26%。有一些方法可以提高你的贏錢機率,但代價是贏錢金額相對於你的總投注金額會減少。
昨晚我玩輪盤賭,用的是「馬丁格爾」策略,第一次輸了之後就加倍兩次。我知道這很蠢,但我通常輸得不多,而且賭博的時間很長。總之,我之所以輸掉這局,是因為我押注相同,結果四次投擲,有三次都出現了數字9。這機率有多大?聽起來可疑嗎?話說回來,賭場有沒有被發現作弊?
4次中任三次任意數字的機率是38*4*(1/38) 3 *(37/38) = 1/5932。然而,如果你玩得夠久,幾乎會忍不住注意到類似的異常情況。這遠不至於引起懷疑。在現實賭場中確實存在作弊行為。通常情況下,被賭場保全抓到的都是不法荷官。雖然有一些針對線上賭場的作弊案件,但據我所知,還沒有政府機構判處任何人有罪。
像大多數玩家一樣,在一次投注中同時投注多個內圈號碼(而非連續投註一個號碼),難道不是更糟糕的輪盤投注策略嗎?例如,假設你手上有 100 美元,那麼在「8」這個數字上投注 10 次,每次 10 美元,比在一次投注 10 個號碼上投注 10 美元損失更小嗎?在我看來,「對沖」只是保證某些投注(在上面的例子中是 9 次)總是會輸嗎?你的頁面上沒有提到「對沖」嗎?
請參閱我的《賭博十誡》 。第六誡是「切勿兩面下注」。關於您的輪盤賭問題,如果一次只押一個數字,則輸掉所有十個數字的機率為 (37/38) 10 = 76.59%。如果一次性將十個數字押在不同數字上,則輸掉所有十個數字的機率為 (28/38) = 73.68%。透過對沖,即一次性押註十個數字,您可以降低全輸的機率,但也將最高贏利限制在 26 美元。如果一次押一個數字,則最高贏利可達 350 美元。這兩種方法的總預期回報率相同,均為 94.74%。
我讀過你關於系統的頁面,而且多年來一直跟別人講這個!我在賭場發輪盤,各種系統我都看過。我看過一個系統,雖然在電腦模擬中可能行不通(很可能永遠行不通),但在現實生活中卻「似乎」行得通。也就是說,我看到它贏的次數比輸的次數多。
它的運作方式是,玩家在1到18的數字上投注75美元,在第三個12的數字上投注50美元,在0到00的數字上投注10美元,總共135美元。這涵蓋了除六個數字(19到22)之外的所有數字,並且每次球未擊中這六個數字時,都會產生15美元的賠付,除非擊中0或00,在這種情況下,賠付40美元。我知道這聽起來很瘋狂! ! !但相信我,我可以告訴你,我看過用這種方法贏的比輸的多。反過來也一樣(廢話)。我很想知道這個系統的真實賠率,但當有人從我的桌子上賺了2000美元時,很難告訴他它不起作用:-)
有30種方式可以贏得15美元,有6種方式可以輸掉135美元,還有2種方式可以贏得45美元(而不是40美元)。這種投注組合的預期回報為((30/38)*15 + (6/38)*-135 + (2/38)*(45))/135 = -0.0526,即5.26%,只要避免可怕的0-0-0-1-2-3組合,任何一種投注或投注組合的賭場優勢就為5.5.5。在你的觀察中,你可能看到的出現次數比預期的要少,只有19-24次,這解釋了為什麼你會誤以為這種方法會贏。
巫師,我在想輪盤賭的事。用Boss Media軟體,你可以不用下注就能轉動輪盤。這不是對玩家有利嗎?我見過的一些輪盤投注系統,像是馬丁格爾系統,輸了就翻倍等等。難道你不能只看著輪盤不下注,然後根據之前的旋轉結果來下注嗎?舉個例子,在下注之前先轉5圈。假設所有數字都是奇數,一開始就押偶數不是比較合理嗎?我知道這有點像賭徒謬誤,輪盤不在乎上次旋轉的結果,而且每次旋轉後,奇數出現的機率都會減少。我是不是明白了什麼道理,還是只是重複一個老理論?
你只是在重複賭徒謬誤。如果球在一個公平的輪盤上連續100次落在奇數位置,那麼下一輪是偶數的機率仍然和每次一樣,在雙零輪盤上是47.37%。所以,即使你不用下注也能旋轉,這根本沒用。球沒有記憶。
雖然輪盤賭顯然不可能靠運氣取勝,但我聽說理論上可以透過兩種物理原理取勝。方法一:使用高科技設備,測量球的速度與輪盤速度的對比,並以大約40%的準確率預測輪盤的結果區域。方法二:輪盤偏差。顯然,輪盤的偏差至少要達到5.26%才能讓玩家保持平衡。問題是,巫師,您覺得需要旋轉多少次才能確定輪盤偏差(如果有的話)?
我聽說過這兩種伎倆都被用過。我對計時輪盤的裝置了解不多,只知道它們確實存在,而且時不時有人使用。在內華達州,這種裝置是絕對違法的。我聽說利用偏差的輪盤犯案的案例更多,而且這種事已經發生過很多次了。我認為使用老式輪盤的賭場是最容易被利用的目標。多年來我一直在說,我認為阿根廷就是一個成熟的目標。
在任何一個均等賠率的輪盤上,用馬丁格爾雙倍投注系統對抗單零輪盤時,我估計你每248次投注中會輸一次。也就是說,一個投注要嘛贏一個單位,要嘛輸255個單位。我的計算正確嗎?如果不正確,能否請您給予正確的賠率?
如果最大損失為255個單位,那麼您最多可以下注8次。連續輸掉8次的機率為(19/37) 8 = 0.004835。因此,您贏得一個單位的機率為99.52%,輸掉255個單位的機率為0.48%。
平均而言,在單零輪盤賭中,在 36 次旋轉過程中,一個數字會重複多少次(例如連續兩個 8)?
每 37 對數字中,預期會出現一次重複。所以,36 個數字對應 35 對數字。因此,預期重複次數為 35/37 = 0.9459。
大家都說,長遠來看,用數學系統是贏不了輪盤賭的。但是,你該如何解釋為什麼有些職業賭徒靠輪盤賭謀生呢?我認為這並非吹牛。他們每天玩輪盤賭,實際上贏的比輸的還要多。
告訴我誰在公平的輪盤賭中贏錢,我就能告訴你誰只是運氣好,很可能會輸光所有錢。你只有巧妙地利用優勢才能在輪盤賭中獲勝,例如利用偏差的輪盤,或精準地控制輪盤。
我讀了你所有關於輪盤賭的內容,但沒看到任何關於輪盤轉盤機的內容。在賭場經理的密切關注下,輪盤轉盤機拋出「部分」來提高賭場的勝率。那些能拋出綠色的轉盤機,雖然不是每次都能,但機率很高,當他想徹底消滅一個大額累積獎金玩家時,大概七八次就能拋出一次。
賭場無需訴諸此類策略即可贏錢。此外,賭場無需害怕累積獎金玩家。大多數累積獎金玩家都能贏錢,但少數達到資金上限的玩家會為所有贏家支付賠款,賭場還會因此損失一部分。此外,要故意將球旋轉到特定區域需要高超的技巧。我認為,這很難做到非常精準。
嗨,巫師,您的網站太棒了。在雙0輪盤賭中,我意識到所有投注都有同樣高的賭場優勢,但我剛完成一門統計學課程,我發現由於標準差的存在,並非所有投注都完全相同。例如,根據我的計算,1美元投注紅色,其標準差為1.012019,而1美元投注單個數字,其標準差為5.839971。因此,在1次、100次和10000次試驗中,等額投注的預期勝出機率分別為0.4793、0.3015和0.0000,而單一數字投注的預期勝出機率分別為0.4964、0.4641和0.1837。我的分析正確嗎? (我假設了常態分佈)謝謝!
謝謝你的讚美。首先,任何等額投注的標準差是0.998614,單一數字的標準差是5.762617。在1、100和10000次旋轉中,透過等額投注平注獲勝的機率分別為0.473684、0.265023和0.00000007。在1、100和10000次旋轉中,透過單一數字平注獲勝的機率分別為0.0263158、0.491567和0.18053280。你似乎想說,單一數字投注更好,因為其獲勝的機率高於多個投注。這話沒錯,但是,巨額虧損的機率也更大。在一個回合中,預期結果總是落在鐘形曲線的某個位置。對於低波動性投注(例如紅色或黑色),鐘形曲線很陡峭,不會偏離小額虧損太遠。對於高波動性投注(例如單一數字),鐘形曲線很寬,允許更大的淨結果範圍,包括好結果和壞結果。
我的同事 D. 堅持說他已經找到了一種在輪盤賭中持續獲勝的完美方法。我不太信服。他是運氣好,還是有什麼有效的方法?
他只是運氣好而已。我已經說過無數次了,沒有任何投注系統可以經得起時間的考驗。
我讀了你在輪盤賭中關於馬丁格爾方法的文章。我在電腦上試過幾次這種方法,贏了500美元。然後我去了賭場,輸了1000多美元。因為黑牌連續出現了8次。但我才剛開始學習百家樂。我之前在電腦上試過,也贏了500美元,因為我押莊。一開始是20美元,然後是40美元,然後是80美元,以此類推。即使每手牌都要支付5%的佣金,我也贏了500美元。你覺得這種方法在賭場行得通嗎?我想在去賭場再輸1000美元之前問問看。就像我說的,黑牌連續出現了8次。但你覺得閒家會連續贏8次嗎?而且,百家樂很好玩,因為平手算輸,在輪盤賭中,0或00算輸。
馬丁格爾策略在每場遊戲中都很危險,長遠來看永遠不會贏。然而,它在百家樂中比在輪盤賭中更適合使用,因為百家樂的莊家優勢更低。玩家連續贏8次的機率是0.493163^8 = 286分之一。另外,請記住,你可能在系列賽後期贏了一手牌,但仍然會因為委託而落後。例如,如果你最初下注1美元,在第7手牌贏了,你將贏得60.80美元(64美元*95%),這不足以彌補之前輸掉的63美元。
你好。你說所有投注系統都會失效。如果你玩輪盤賭,在1-12號投註一個單位,在13-24號投注兩個單位,那麼你贏錢或不贏錢的機率是不是有66.66%?
不完全是。您有 12/38 的機率贏得 3 個單位,12/38 的機率不贏不賠,14/38 的機率輸掉 3 個單位。預期值為 [(12/38)*3 + (12/38)*0 + (14/38)*-3]/3 = (-6/38)/3 = -2/38 = -5.26%。任何投注組合都適用,只要您避開可怕的 5 個數字組合 (0/00/1/2/3)。如果您只玩一輪,並且想要最大化您的獲勝機率,那麼請在 35 個數字上均等投注。您將有 92.11% 的機率贏得 1 個單位,而輸掉 35 個單位的機率為 7.89%。
你好。我玩輪盤賭已經好幾年了,這是我第一次考慮嘗試輪盤賭系統……現在我知道你對這些所謂的「系統」以及它們背後的騙子是什麼感覺了。相信我,我也有同樣的感受,但我遇過兩個不容忽視的系統…
第一個是 RD Ellison 著作《賭贏:輪盤》中的 3q/A 策略,其驗證勝率為 7.94%(7500 次旋轉)。該系統由 Frank Scoblete 的《Spin roultte Gold》和 Eric St. Germain 的《輪盤系統測試員》共同測試開發。
第二個是 Don Young 的輪盤系統,該系統經過驗證,擊敗了 Zumma Publishing 的輪盤系統測試儀(15000 次旋轉)。
現在,我必須要說,我對花錢買這些系統還是有點懷疑,但既然它們已經經過長期考驗,我實在找不到不買的理由。我的意思是,打敗這些考試題庫肯定意味著什麼…
你對這些系統有什麼看法?你覺得我應該嘗試嗎?
非常感謝!祝您今天愉快。祝一切順利
7500次旋轉?就這些嗎?如果下注積極,任何人都可以在7500次旋轉中獲得相當於總投注金額7.94%的利潤。 15000次旋轉也是如此。大多數系統的設計初衷就是為了獲得大量小額收益和少量巨額虧損。一個需要巨額資金的系統很容易在15000次旋轉後就獲利。但最終虧損會接踵而至,它經不起時間的考驗。巨額虧損也可能在一開始就出現。檢驗一個系統的真正方法是進行數十億次的試驗。我對這些系統的看法和所有系統一樣,它們一文不值。我不介意你嘗試一下,但我不介意有人把一分錢塞進賣主的口袋裡。
注意:請參閱下一欄對此問題的後續內容。
親愛的先生,在單零輪盤遊戲中,如果您在更多次旋轉中將部分資金押在較少的數字上,而不是每次旋轉都押在更多數字上,那麼您獲勝的概率就會增加。例如:如果您願意冒 500 美元的風險贏得 250 美元,那麼您可以:選項 (A):在兩打中的任意一打上押 250 美元,如果您贏了,您將贏得 250 美元。發生這種情況的機率是 24/37=(0.648648)。選項 (B):在任何一打上押 125 美元,如果您贏了,您將贏得 250 美元並離開。但是,如果您輸了,您現在可以在同一個打上押 187.5 美元,如果您贏了,您將贏得 375 美元,這將使您獲得 250 美元以及您在上一次旋轉中輸掉的 125 美元。現在,即使兩次都輸了,您仍然有 187.5 美元可用,您可以在任何九個數字上投注 20.833333 美元,如果您贏了,您將獲得 750 美元,這相當於您的 500 美元原始資金加上您的目標獎金 250 美元。這種情況發生的可能性是,在三次旋轉中至少一次擊中 12 個或 9 個數字,其機率等於 [1-(25/37)x(25/37)x(28/37)]=0.65451。因此,對於相同的資金和相同的回報,如果您投注更少的數字和更少的錢,但可能旋轉更多次,您就可以像選項 (B) 那樣提高成功的機率。 (因為您可能在第一次旋轉中獲勝)如果您一次只投註六個數字並嘗試贏得 250 美元,您甚至可以進一步提高您的機率。有什麼解釋嗎? ! ! ! !我向您致以最崇高的敬意,並期待您的回覆。
您說得對,儘管目標和本金相同,但選項B的成功機率更大。原因是選項B的平均投注金額較小,因此您的資金承受的莊家優勢較小,從而獲勝的機率更高。選項A的投注金額始終為500美元。選項B的平均投注金額為(12/37)*125 + (25/37)*(12/37)*(125+187.5)+ (25/37)*(25/37)*(125+187.5+187.5) = 337.29。
當我參加拉斯維加斯挑戰賽時,離比賽結束還有幾分鐘,我手頭上大約有8000美元,需要至少贏到24000美元。所以我把資金分成四堆,每堆2000美元,每堆都押註一個4個數字的組合,每個組合的賠率是22000美元。這樣,我就不必把全部賭注都押在賭場優勢上,這增加了我贏錢的機率。
如果在輪盤賭上押注全部 38 個數字,那麼即使在短時間內也不可能戰勝賠率,如果每個數字押注 1 美元,那麼每次轉動輪盤就會損失 2 美元。 (0、00 輪盤,沒有對等額賭注的有利規則)根據統計數據確定一個最佳的賭注數字範圍,這看起來合理嗎?
我衡量投注價值的標準是預期回報,而不是中獎機率。因此,投注全部38個數字的莊家優勢為2/38 = 5.26%,與投注單一數字或任多個數字的莊家優勢相同。雖然投注全部38個數字淨贏的機率為0%,但缺點是只損失總投注金額的5.26%。如果被迫投注,並且希望最小化差異,那麼您應該投注全部38個數字。舉個實際的例子,如果您有促銷籌碼需要下注,而您不想冒險,那麼就投注所有籌碼以獲得準確的預期價值。因此,回答您的問題,沒有最佳的數字範圍。所有範圍的預期價值都相等。
今天有個故事,講的是一位英國男子,他願意把畢生積蓄都押在一次輪盤賭上。我和我的朋友一直在爭論,對於這種類型的賭注,賭場裡最好的選擇是什麼。如果你只能下註一次,並且希望最大化你的賠率,那麼最好的遊戲是什麼?最好的選擇又是什麼?
首先,我要說這傢伙是個傻瓜。他在一個普通的美式輪盤賭上押了13.8萬美元,這個輪盤有兩個零,賭場優勢是5.26%。這相當於預期損失7,263美元。然而,如果他坐10分鐘的車去百樂宮、幻影酒店或阿拉丁酒店,他完全可以在單零輪盤賭上押注,因為單零輪盤遵循歐式規則,如果球落在零上,他會退還一半的等額投注。反正他打算押等額投注。所以,在這些完全遵循歐式規則的輪盤賭上,他的賭場優勢只有1.35%,預期損失只有1865美元。
回答你的問題,如果被迫只進行一次等額賭注,我會選擇百家樂中的莊家賭注,其賭場優勢為 1.06%。
如果輪盤賭採用以下投注模式,我的破產風險有多大?
破產風險問題在數學上很複雜。除非是簡單的輸贏遊戲,否則我建議在電腦上進行隨機模擬。
我住在新澤西州,距離大西洋城以北約兩小時車程。你知道離我家最近的歐洲輪盤賭在哪裡嗎?
大西洋城有很多單零輪盤。那裡的大多數賭場都有,但最低投注額為25美元。
我當時在Casino On Net賭場玩輪盤賭。我押的是穩當的注,只押在第一個12(大注)、第二個12(中註)和第三個12(高注)。我轉了5圈都沒下注,等著某個組合的圖案不出現,就押注,希望這能改變我中獎的機率。 5圈之後,大注沒出現。我繼續押大注,我猜1、2、3、4、5、6、7、8、9、10、11或12會在12圈內出現,這樣至少能贏回我的錢……但並沒有。賭桌連續轉了17圈,都沒出現小注,我的獎金從258美元降到了0美元……反正都是獎金。這個問題分為三個部分:
- 我等待 5 次旋轉而沒有出現小數字是否真的增加了出現 L 的機率?
- 低數字連續 16 次不出現的機率是多少?
- 低數字連續 17 次不出現的機率是多少?
謝謝,我也想感謝你的那本《二十一點指南》,我用你的方法把 5.00 美元變成了 100.00 美元。
- 不
- Casino on Net 使用單零輪盤。因此,出現 16 次零的機率為 (25/37) 16 = 0.1887%。
- (25/37) 17 = 0.1275%。
莊家在輪盤賭 10 次旋轉中得到 5 個相同數字的機率是多少?
在雙零輪盤遊戲中,任意數字在 10 次旋轉中恰好出現 5 次的機率可以近似為 38* combin (10,5)*(1/38) 5 *(37/38) 5 = 1/359275。
恭喜你創建了一個很棒的網站。我完全理解你對21點賠率6比5的差距感到憤怒,但我也很好奇為什麼美國人似乎毫無異議地接受了00輪盤賭。這種輪盤賭簡直是犯罪,應該和基諾和老虎機並列。
謝謝。你說得對。通常情況下,6比5二十一點的莊家優勢是1.44%,而雙零輪盤賭的莊家優勢是5.26%。這差了3.7倍。然而,這些年來我的經驗是,無論莊家優勢有多差,要讓玩家離開他們喜歡的遊戲幾乎是不可能的。所以我能做的最好的就是建議他們如何玩他們喜歡的遊戲。對二十一點玩家來說,3比2的遊戲仍然不缺。玩6比5會為賭場帶來額外的0.8%的優勢,這毫無道理。我還強調,如果你是輪盤賭玩家,尋找單零輪盤賭非常重要。所以我認為兩者並無矛盾。
能否請您解釋一下輪盤賭的賭桌限額是如何運作的,以及單一號碼和賭桌的最低限額之間有什麼區別?如果可以的話,請舉例說明。
輪盤賭通常有兩個最低投注。例如:外圍投注 5 美元,內圍投注 1 美元。外圍投注包括所有等額投注、列註和十二註。內圍投注則指投注數字,包括 2、3、4、5 和 6 的數字組合。在這種情況下,外圍投注的最低投注額為 5 美元,內圍投注的最低投注額為 1 美元。但是,內圍投注的總投注額必須至少為 5 美元,否則不投注。
我在賭場工作,有人打賭說輪盤荷官無法影響擲骰結果。一定有人認為可以。當然不是影響某個數字,而是影響輪盤的某個部分。你認為一個好的測驗能合理地確定荷官是否影響了結果嗎?假設試驗次數合理,我很樂意分享結果。
我站在你這邊。如果真能做到這一點,那麼荷官就能輕易地與玩家合謀,瓜分利潤。但我從未聽過這種情況。一個很好的測試方法是找一個聲稱能夠影響擲骰結果的人,讓他在 100 次旋轉中盡可能多地嘗試將骰子投到輪盤的特定半邊。他嘗試的次數越多,他的說法就越有說服力。下表顯示了 50 到 70 次旋轉成功的機率。例如,60 次或更多次旋轉成功的機率是 2.8444%。統計學中常見的置信閾值是 90%、95% 和 99%。要通過 90% 置信度測試(其中隨機旋轉失敗的機率為 90%),成功旋轉的次數需要達到 57 次或更多。要通過 95% 的測試,成功旋轉的次數需要達到 59 次或更多,而 99% 的測試則需要達到 63 次或更多。
至少 50 到 70 次輪盤賭成功旋轉的機率
| 勝利 | 可能性 |
| 70 | 0.000039 |
| 69 | 0.000092 |
| 68 | 0.000204 |
| 67 | 0.000437 |
| 66 | 0.000895 |
| 65 | 0.001759 |
| 64 | 0.003319 |
| 63 | 0.006016 |
| 62 | 0.010489 |
| 61 | 0.0176 |
| 60 | 0.028444 |
| 59 | 0.044313 |
| 58 | 0.066605 |
| 57 | 0.096674 |
| 56 | 0.135627 |
| 55 | 0.184101 |
| 54 | 0.242059 |
| 53 | 0.30865 |
| 52 | 0.382177 |
| 51 | 0.460205 |
| 50 | 0.539795 |
www.ccc-casino.com 有無零輪盤,他們稱之為超級機會輪盤。有沒有其他系統可以有效應付沒有零的情況?如果沒有零,玩家可以同時有效地玩紅黑輪盤嗎?因為不用擔心零。
我試圖找到那個遊戲,但當我查看時,網站已經癱瘓了。然而,假設這樣的遊戲確實存在,答案是否定的。從長遠來看,沒有任何系統能夠擊敗它,也不會輸給它。每個系統的預期值都恰好為零。
單0輪盤。任一個數字(0-36)在連續三次旋轉中出現多次的機率是多少?感謝您抽出時間!
無論第一個數字是多少,只有第二個旋轉匹配它的機率是 (1/37)*(36/37)。只有第三個旋轉匹配它的機率是 (36/37)*(1/37)。兩個旋轉都不匹配,但第二個和第三個旋轉互相匹配的機率是 (36/37)*(1/37)。第二個和第三個旋轉都符合它的機率是 (1/37)*(1/37)。將所有這些加起來,您將得到 3*(1/37)*(36/37)+ (1/37)*(1/37) = 7.962%。
我想你可能會對此感興趣。我在英國用的是Betfair。我敢肯定你們這些好心人在美國因為某些原因不能用它。如果你不熟悉它,可以去betfair.co.uk看看。它是一個博彩交易所,不是博彩公司。總之,我的問題是:他們現在提供無零輪盤,沒錯,就是無零輪盤。這確實是真的。你能想到一個好的策略嗎?如果有的話,你會保密嗎?祝好,喬納森。 P.S.:他們也提供其他沒有莊家優勢的賭場遊戲。
我嘗試在那裡註冊一個帳戶來查看情況,但他們封鎖了美國玩家。我被告知最低投注額為2英鎊,最高投注額為50英鎊。即使是像無零輪盤這樣的零莊家優勢遊戲,也沒有任何投注系統能夠超過或低於0%這個數字。無論你做什麼,你投注的越多,實際莊家贏利就越接近0%。
你說輪盤沒有必勝法。貢薩洛·加西亞-佩拉約和他的家人在世界各地的許多賭場贏了很多錢。他們甚至出版了一本書,描述了他們是如何做到的。你對此有何看法?
我曾經看過一個關於他的電視節目,我很欣賞他的做法。我所定義的「系統」是指一種投注模式,例如馬丁格爾策略,應用於具有莊家優勢的遊戲,例如公平的輪盤賭。 Gonzalo Garcia-Pelayo成功做到的是調查球落在每個數字上的機率,以便發現並利用存在偏差的輪盤賭機制。我稱之為策略,而不是系統。有很多可以擊敗賭場的獲利策略,但卻沒有獲利的投注系統。
如果我向您展示一款沒有零的輪盤遊戲,並且所有常見的輪盤規則都適用,那麼有可能 100% 獲勝嗎?
不。
我長期訂閱你們的時事通訊,並且仍然很喜歡你們的網站。我偶然發現一個賭場網站,它提供的輪盤賭沒有零,只有1-36的數字,並且所有標準的輪盤賭規則都適用。你們有辦法利用這一點嗎?我知道你們不喜歡投注系統,但這個網站沒有莊家優勢。肯定有一個資金管理系統,可以在這些賭桌限額下獲利。任何建議都非常感謝。
謝謝你的讚美。我想我之前回答過這個問題,但答案是否定的。即使沒有賭場優勢,從長遠來看,仍然沒有任何投注系統能夠獲勝。
您好,出於顯而易見的原因,如果您不告訴任何人我的名字,我將不勝感激。在我工作的賭場,輪盤荷官幾乎一致認為,他們可以“控制旋轉”,輕鬆擊中輪盤的某些部分,或者故意錯過其他部分。考慮到輪盤中球旋轉的所有因素,包括球側面的凸起(凸起)、球的方向和輪盤的速度等等——您覺得這有什麼意義嗎?一個不誠實的荷官就能幫助玩家克服巨大的賭場優勢嗎?
這遠非我第一次聽到這種說法,我對此深表懷疑。大多數荷官也相信一些流言蜚語,例如糟糕的三壘手會導致其他玩家在二十一點遊戲中輸錢,所以總的來說,他們並不是最懷疑的一群人。我認為真正的原因是,他們記得自己成功控制旋轉的次數,卻輕易忘了失敗的次數。就像他們記得三壘手搶走荷官爆牌的次數,卻忘了他拯救牌桌的次數一樣。
如果荷官真能做到這一點,那麼很容易就能找到同夥,讓他贏,讓其他玩家輸,以此來彌補損失。只要他們按照正確的程序進行旋轉,並且不與同夥一起出現在公共場合,這一切看起來就完全合法。然而,你從未聽過這種事。我想那些相信的人可能會說,這樣做的人只是在保持低調,但那些相信毫無價值的投注系統的人也會這麼說。如果這真的像你工作的輪盤賭荷官說的那麼容易,那麼由此產生的作弊問題就會非常猖獗。
在雙零輪盤賭中,第 200 次旋轉時任何數字都不會出現的機率是多少?
任何給定數字不會命中的機率是 (37/38) 200 = 0.48%。
對於 38 個數字,我們可能會錯誤地說其中任何一個數字都不會被擊中的機率是 38 × (37/38) 200 = 18.34%。
這是不正確的,因為它重複計算了兩個未中數字的機率。所以我們需要減去這些機率。 38 個數字中,有(38,2) = 703 組,每組 2 個。任兩個給定數字未中機率為 (36/38) 200 = 0.000020127。我們需要減去兩個數字都未中的情況。因此,我們得到:
38×(37/38) 200 - 組合(38,2)×(36/38) 200 = 16.9255%。
然而,現在我們已經抵消了三個號碼未中獎的機率。對於任何給定的三個號碼組,我們將任意一個號碼未中獎的機率計算三次。然後,我們分別減去三次,從三個號碼中選出兩個號碼,最後三個號碼全部未中獎的機率為零。共有 combin(38,3)=8,436 個這樣的組別。將它們加回去,我們現在得到:
38×(37/38) 200 - 組合(38,2)×(36/38) 200 + 組合(38,3)×(35/38) 200 = 16.9862%。
然而,現在我們高估了四個號碼未中獎的機率。對於 combin(38,4)=73,815 組四個號碼中的每一組,最初都計算了四次。然後,我們減去了 combin(4,2)=6 組(每組 2 個號碼)中的每一組。之後,我們又加回了 4 組(每組 3 個號碼)的 3 個號碼。因此,對於每個四個號碼的並集,它被計算了 4 − 6 + 4 = 2 次。為了調整重複計算,我們必須對每一組進行減法。減去這些數字後,我們現在得到:
38×(37/38) 200 - 組合(38,2)×(36/38) 200 + 組合(38,3)×(35/38) 200 - 組合(38,4)×(34/38) 200 = 16.9845%。
繼續這個過程,我們會不斷交替進行加減運算,直到失去37個數字。因此,至少一個數字永遠不會被選中的機率是:
總和 i=1 至 37 [(-1) (i+1) × combin(38,i) × ((38-i)/38) 38 ] = 16.9845715651245%
以下是對 126,900,000 個這樣的 200 次旋轉實驗進行隨機模擬的結果。
200 次輪盤賭中命中的數字
| 數字命中 | 觀察 | 比率 |
|---|---|---|
| 31歲或以下 | 0 | 0 |
| 三十二 | 1 | 0.00000001 |
| 33 | 33 | 0.00000026 |
| 三十四 | 1812 | 0.00001428 |
| 三十五 | 68845 | 0.00054251 |
| 三十六 | 1577029 | 0.01242734 |
| 三十七 | 19904109 | 0.15684877 |
| 三十八 | 105348171 | 0.83016683 |
| 全部的 | 126900000 | 1 |
至少一個數字未被擊中的次數比率為 0.169833。
我有個朋友是賭場工作人員,負責看管輪盤賭桌。他告訴我,每當有人開始贏錢,賭場就會換荷官。我還看過工作人員要求荷官以不同的速度旋轉輪盤。這不就代表賭場確信荷官能夠讓一系列非隨機的數字出現嗎?這不就代表賭徒可以去尋找「幸運」賭桌,荷官的旋轉速度越快,他們贏錢的幾率就越大嗎?
可悲的是,無知的程度甚至會上升到相當高的程度。我並不否認專家可以計算出輪盤旋轉速度有多慢。然而,撇開這個問題不談,更換荷官並不能改變賠率。沒有幸運或不幸的荷官之說。迷信很難戒除。正如我多次說過的,一種信念越荒謬,就越容易被人們固執地堅持下去。
先生,我玩了8672場自動單零輪盤遊戲。我預設的號碼竟然出現了278次。我選擇這個號碼是因為口袋的磨損。我怎麼確定這個號碼的機率高於1/37呢?
如果我的術語正確的話,「預測輪盤」是指根據球速、球位置和輪盤速度來預測球的落點。聽起來你的做法是利用偏向性輪盤,這是一種不同的優勢玩法。既然我們討論的是這個話題,那麼第三種優勢玩法就是利用“荷官簽名”,荷官的玩法非常穩定,以至於每次旋轉球和輪盤的速度幾乎都相同。這使得玩家能夠根據球的位置和過往結果來預測球的落點。
回答你的問題,你預期中獎的次數是 8672/37=234.38。變異數是 8672×(1/37)×(36/37)=228.04。標準差是變異數的平方根,即 15.10。你的中獎次數比預期多了 278-234.38=43.62。也就是 (43.62-0.5)/15.10 = 2.8556 個標準差。減去 0.5 的原因很難解釋。簡而言之,這是一個使用連續函數估計離散函數的調整因子。進行高斯近似,中獎次數達到或超過這個數字的機率是 0.21%。所以,你很有可能遇到了一個有偏差的輪盤。然而,仍有 1/466 的可能性,這只是運氣好而已。
20年前,日本豪賭客柏木與唐納德·川普之間發生了一場著名的淘汰賽。柏木在百家樂中每手的投注不得超過20萬美元。當賭場或玩家領先1200萬美元時,遊戲就會結束。假設柏木總是在莊家上押最大注,那麼柏木獲勝的機率是多少?
如果他押注閒家,計算起來就容易多了。我在我的 mathproblems.info 網站上算過一個類似的輪盤賭題,題號 116。對於等額投注,通用公式是 ((q/p) b -1)/((q/p) g -1),其中:
b = 起始資金(以單位計)。
g = 資金目標(以單位計)。
p = 贏得任何給定賭注的機率,不包括平局。
q = 在任何給定賭注中失敗的機率,不包括平局。
此處,玩家初始資金為1200萬美元,即60個單位,每個單位20萬美元,並將一直玩到資金達到120個單位或破產。因此,在玩家下注的情況下,等式值為:
b = 60
克= 120
p = 0.493175
q = 0.506825
所以答案是 ((0.506825/0.493175) 60 -1)/(( 0.506825/0.493175) 120 -1) = 16.27%。
由於莊家投注有5%的佣金,情況要複雜得多。這會導致玩家超額完成目標的可能性很高。如果我們增加一條規則:如果贏錢的賭注能夠幫助玩家實現目標,那麼他只需下注達到1200萬美元所需的金額,那麼我估計他成功的機率為21.66%。
資金翻倍機率的一個更簡單的公式是 1/[1+(q/p) b]。
這個問題是在我的同伴網站Wizard of Vegas的論壇中提出並討論的。
平均而言,在 38 個數字的輪盤賭中,需要進行多少次試驗才會重複出現任何數字?
計算第一次試驗,我顯示平均值為 8.408797,中位數為 8,眾數為 7。
兩個數字不重複的機率是 37/38 = 97.37%。
三個數字不重複的機率是(37/38)×(36/38)= 92.24%。
四個無重複數字的機率為 (37/38)×(36/38)×(35/38) = 84.96%。
依照這個模式,8 個數字中沒有重複的機率是 (37/38)×(36/38)×(35/38)×...×(31/38) = 45.35%。
因此,8 個數字內重複的機率為 100% - 45.35% = 54.65%。
我猜大多數人會認為8個數字以內重複的機率會低於這個數字。如果你不介意佔你數學不好的朋友的便宜,可以跟他們打賭,至少有一個數字重複的機率是8個或更少。這樣你就押8個或更少,你的朋友押9個或更多。如果他/她猶豫不決,那就押7個或以上,這樣贏的機率是55.59%。基本上,任何一方的中位數是8的一方都有可能贏。
這個問題是在我的同伴網站Wizard of Vegas的論壇中提出並討論的。
探索頻道的《Hustling the House》節目中有一長段節目,探討如何將30美元變成1000美元。節目中,安迪·布洛赫說:「如果你口袋裡有30美元,你想把它變成1000美元,那麼輪盤賭是你唯一的選擇。」安迪接著解釋了為什麼把全部30美元押在一個數字上比五次等額投注更好。
安迪說得對,將 30 美元變成 1,000 美元的最佳方式是將全部 30 美元押在輪盤賭中的一個數字上,對嗎?
不,他錯了。安迪的單註策略的機率是1/38 = 2.6316%。
經過多次反覆試驗,我設計出了「萬福瑪利亞」輪盤策略,將 30 美元變成 1,000 美元的幾率提高到 2.8074%。
巫師的輪盤賭「萬福瑪利亞」策略:
此策略假設投注必須以 1 美元為增量。所有投注計算均向下取整。
讓:
b = 您的資金
g = 你的目標
- 如果 2*b >=g,則在任何等額賭注上投注 (gb)。
- 否則,如果 3*b >=g,則在任意列上投注 (gb)/2。
- 否則,如果 6*b >=g,則在任意六行(六個數字)上投注 (gb)/5。
- 否則,如果 9*b >=g,則在任意角(四個數字)下注 (gb)/8。
- 否則,如果 12*b >=g,則在任意街道(三個數字)上投注 (gb)/11。
- 否則,如果 18*b >=g,則在任何分割(兩個數字)上投注 (gb)/17。
- 否則,對任意單一數字下注 (gb)/35。
換句話說,盡量只用一次投注就達到目標,但不要超過目標金額。如果有多種方法可以實現目標,那就選擇獲勝機率最大的那個。
你可能會問,其他遊戲怎麼樣?探索頻道的配音員說:「大家都同意輪盤賭是賭場裡最好的快速致富計畫。」 好吧,我不這麼認為。即使只限於常見的遊戲和規則,我也覺得擲骰子比較好。尤其是在押注不及格和下注賠率方面。
按照我的擲骰子「萬福瑪利亞」策略(下文會解釋),30 美元變成 1,000 美元的機率是 2.9244%。這假設玩家可以下注 6 倍賠率,無論點數是多少(即允許 3 倍、4 倍或 5 倍賠率下注的情況)。這個成功機率比我的輪盤「萬福瑪利亞」策略高 0.117%,比安迪·布洛赫策略高 0.2928%。
安迪可能會辯稱,我上述論點依賴最低下注額為 1 美元的假設,這在拉斯維加斯的真人荷官遊戲中很難實現。考慮到有人會這麼說,我把最低下注額設為 5 美元,並以 5 美元為增量進行下注,並以此為前提,玩了兩局遊戲。在這種情況下,使用我的「萬福瑪利亞」策略,在輪盤賭中獲勝的機率為 2.753%,在擲骰子中獲勝的機率為 2.891%。這兩種情況下,都高於安迪·布洛赫策略下的 2.632%。
平心而論,探索頻道絕不會把上面那段瘋狂的咆哮搬上電視,他們肯定想找一些大眾能理解的簡單易懂的內容。安迪肯定在跟他們講他們想聽的東西。他建議的基本前提是,如果你想達到某個目標,那麼「打了就跑」的策略比讓賭場優勢把你壓垮在多重賭注下要好得多。這絕對是真的,也是我17年來一直在宣揚的理念。
巫師的擲骰子「萬福瑪利亞」策略。
此策略假設投注必須以 1 美元為增量,且贏取的金額將向下取整至最接近的美元。計算投注時,切勿下注過多,以免超出目標金額。此外,切勿下注超過四捨五入金額。
讓:
b = 您的資金
g = 你的目標
- 在不通過的情況下下注 max($1,min(b/7,(gb)/6))。
- 如果擲出一個點,並且你的籌碼足夠進行全額賠率投注,那麼就押全額賠率。否則,盡可能押注。
所以,我希望安迪和探索頻道能夠開心。我花了好幾天進行模擬,就是為了證明他們錯了。
這個問題是在我的「拉斯維加斯巫師」論壇上提出並討論的。
輪盤賭中,第 4、5、6、7、8 或 9 次旋轉內球落在 1、2 和 3 的機率是多少?
一般公式為:
Pr(球落在 1) + Pr(球落在 2) + Pr(球落在 3) - Pr(球落在 1 和 2) - Pr(球落在 1 和 3) - Pr(球落在 2 和 3) + Pr(球落在 1、2 和 3)。
在雙零輪盤賭中,對於 n 次旋轉,結果為 3*(1-(37/38)^n)-3*(1-(36/38)^n)+(1-(35/38)^n)。
下表顯示了單零和雙零輪盤賭中從 3 到 100 次旋轉中滾動出所有三個數字的機率。
輪盤問題
| 旋轉 | 單身的 零 | 雙倍的 零 |
|---|---|---|
| 3 | 0.000118 | 0.000109 |
| 4 | 0.000455 | 0.000420 |
| 5 | 0.001091 | 0.001009 |
| 6 | 0.002094 | 0.001939 |
| 7 | 0.003518 | 0.003261 |
| 8 | 0.005404 | 0.005016 |
| 9 | 0.007785 | 0.007234 |
| 10 | 0.010684 | 0.009937 |
| 15 | 0.033231 | 0.031066 |
| 20 | 0.068639 | 0.064476 |
| 二十五 | 0.114718 | 0.108254 |
| 三十 | 0.168563 | 0.159750 |
| 三十五 | 0.227272 | 0.216265 |
| 40 | 0.288292 | 0.275379 |
| 45 | 0.349548 | 0.335089 |
| 50 | 0.409453 | 0.393835 |
| 55 | 0.466865 | 0.450467 |
| 60 | 0.521017 | 0.504191 |
| 65 | 0.571445 | 0.554501 |
| 70 | 0.617922 | 0.601122 |
| 75 | 0.660393 | 0.643951 |
| 80 | 0.698930 | 0.683016 |
| 85 | 0.733693 | 0.718435 |
| 90 | 0.764897 | 0.750386 |
| 95 | 0.792791 | 0.779086 |
| 100 | 0.817638 | 0.804773 |
在墨西哥的某些賭場,輪盤賭用骰子代替輪盤。規則如下:
- 有四個骰子──兩個綠色,一個紅色,一個藍色。
- 如果兩個綠色骰子都落在一個點上,則「旋轉」的結果為零。
- 如果兩個綠色骰子都落在六上,那麼「旋轉」的結果將是雙零。
- 如果綠色骰子出現任何其他結果,則紅色和藍色骰子的 36 種可能結果應對應到數字 1 和 36 以表示「旋轉」。
與傳統輪盤賭相比,這會如何改變賠率?
0和00的中獎機率分別為1/36。如果投注這些結果的賠率是通常的35比1,那麼賭場優勢就剛好是0%。
其他任何數字的中獎機率為 (34/36)*(1/36) = 2.62%。相較之下,傳統雙零輪盤的中獎機率為 1/38=2.63%。投注 1 至 36 的莊家優勢為 5.56%。相較之下,傳統雙零輪盤的莊家優勢為 5.26%。我建議在這款遊戲中只投注零和雙零。
如果有人可以確認或否認這些規則和報酬,請告訴我。
我記錄了7456次輪盤賭的旋轉。結果如下。我懷疑輪盤有偏差,但不確定數據是否足夠確鑿,可以玩這個遊戲。
輪盤數據
| 獲勝 數位 | 發生 |
|---|---|
| 0 | 204 |
| 二十八 | 214 |
| 9 | 175 |
| 二十六 | 177 |
| 三十 | 203 |
| 11 | 181 |
| 7 | 223 |
| 20 | 205 |
| 三十二 | 184 |
| 17 | 222 |
| 5 | 224 |
| 22 | 241 |
| 三十四 | 194 |
| 15 | 210 |
| 3 | 209 |
| 24 | 176 |
| 三十六 | 203 |
| 十三 | 217 |
| 1 | 217 |
| 00 | 197 |
| 二十七 | 173 |
| 10 | 195 |
| 二十五 | 198 |
| 二十九 | 217 |
| 12 | 197 |
| 8 | 207 |
| 19 | 163 |
| 31 | 180 |
| 18 | 201 |
| 6 | 186 |
| 21 | 203 |
| 33 | 171 |
| 16 | 164 |
| 4 | 200 |
| 23 | 191 |
| 三十五 | 163 |
| 14 | 177 |
| 2 | 194 |
| 全部的 | 7456 |
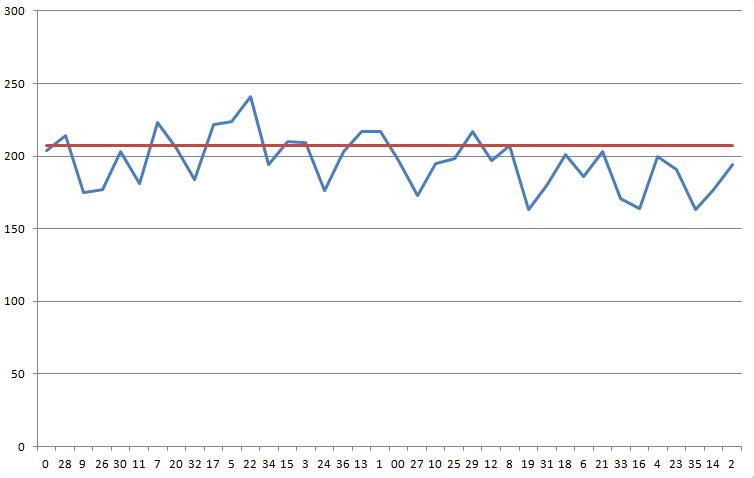
下圖按順序顯示了您在輪盤上的結果。藍線表示您的結果。紅線表示您需要的數字 207.11,以克服 5.26% 的賭場優勢。
對此分佈進行卡方檢定,結果顯示自由度為 37,統計量為 68.1。出現這種或以上偏態分佈的機率為 1/725。
我認為卡方檢定並非適用於這種情況的最佳方法,因為它沒有考慮結果的順序,但我也不知道有更好的檢定方法。有人建議使用Kolmogorov-Smirnov 檢驗,但我認為這並不合適。如果有其他適當的檢驗方法,我洗耳恭聽。
我可以說,如果你押注圍繞數字5的3個數字弧,那麼你記錄的旋轉次數將獲得10.57%的利潤。然而,如果你押注圍繞數字5的7個數字弧,利潤率就會下降到2.84%。
如果非要用簡單易懂的語言來回答,我會說輪盤確實有偏見,但並非確鑿無疑的證據。然而,這種偏見可能不足以顯著且自信地克服賭場優勢。假設賭場不在賭桌之間調換輪盤,我認為在下大注之前應該收集更多數據。很抱歉,我的回答如此模稜兩可。
這個問題是在我的「拉斯維加斯巫師」論壇中提出並討論的。
在單零輪盤賭中,每個數字至少出現一次所需的平均旋轉次數和中位數是多少?
求平均值要容易得多,所以我們就從平均值開始。讓我們一步一步來:
- 第一次旋轉肯定會出現一個新數字。
- 第二次旋轉出現新數字的機率為 36/37。若某事件的機率為 p,則該事件發生的預期嘗試次數為 1/p。在這種情況下,出現第二個數字的預期嘗試次數為 37/36 = 1.0278。
- 觀測到兩個數字後,下次旋轉出現新數字的機率為35/37。因此,觀測到第二個數字後,預期旋轉次數為37/35 = 1.0571。
- 依照這個邏輯,看到每個數字的平均旋轉次數是 1 + 37/36 + 37/35 + 37/34 + ... + 37/2 + 37/1 = 155.458690。
中位數要複雜得多。為了找到確切的答案,與使用隨機模擬不同,我們需要運用大量的矩陣代數運算。我已經在其他「問巫師」問題中討論過如何解決類似的問題,因此不再贅述。類似問題的一個例子是連續三次擲出一對 6-6 的機率,正如「問巫師」#311中所討論的。可以說,在 145 次旋轉中看到所有數字的機率是 0.49161779,在 146 次旋轉中看到所有數字的機率是 0.501522154。因此,中位數是 146。
我在Wizard of Vegas論壇上提出並討論了這個問題。
如果一個球在輪盤賭的最後20次旋轉中都落在紅色,那麼下一次旋轉落在黑色的概率是多少?
與紅色相同,在雙零輪盤上的機率為47.37%,即18個黑色數字除以總共38個數字。
我認為你對前一個問題的看法是錯誤的。連續出現21次紅色的機率是(18/38)21,也就是1比6,527,290。這種情況下,出現黑色的機率絕對佔壓倒性優勢。
確實如此,但這並不重要。這與連續出現20次紅色後出現黑色的概率是相同的。事實上,在輪盤賭這類獨立試驗的遊戲中,過去的結果並不影響未來。
我想出了一個在輪盤賭上擊敗賭場的方法!首先在任何等額賭注上下小注,比如紅色或黑色。如果輸了,就在同樣的選項上加倍下注。然後一直加倍,直到贏為止。最終肯定會贏,而當贏的時候,我就能賺回最初的賭注。然後重複這個過程。你覺得怎麼樣?還有,請不要告訴任何人。
這可能是所有賭博系統中最為人所知的一種,稱為「馬丁格爾」。賭徒們自古以來便構思並使用它。如同所有賭博系統,它不僅無法克服莊家的優勢,甚至無法對其造成絲毫影響。原因在於賭徒終將遭遇一段糟糕的連敗,使得其資金不足以再次加倍下注。
在你之前的回答中,你解釋了為什麼馬丁格爾策略無效。那麼相反的策略呢?即在每次獲勝後加倍下注,直到達到預期目標?
這被稱為反馬丁格爾策略,同樣毫無價值。當你的資金被逐漸磨損至零的次數,將超過你達到目標時的贏利。無論你使用何種投注系統,或根本不使用任何系統,玩的次數越多,你在雙零輪盤中損失的金額與投注金額的比例將越接近5.26%。
輪盤賭需要旋轉幾次才能連續出現五個紅色或五個黑色?
[/spoiler] 答案是 3872789/118098 =~ 32.79301089 次旋轉。 [/劇透]
這是我的解決方案(PDF)。
輪盤賭中的「三分法」是什麼?
「三分法」指出,如果輪盤上的每個數字都旋轉一次,則大約有 1/3 的數字永遠不會出現。
1/3 確實是相當糟糕的估計。更好的估計值應該是 1/e =~ 36.79%。雙零輪盤的真實百分比是 36.30%。
下表顯示了在 38 次雙零輪盤旋轉中觀察到 1 到 38 個不同數字的機率。
三分法-雙零輪盤賭
| 清楚的 數位 | 可能性 |
|---|---|
| 1 | 0.000000000 |
| 2 | 0.000000000 |
| 3 | 0.000000000 |
| 4 | 0.000000000 |
| 5 | 0.000000000 |
| 6 | 0.000000000 |
| 7 | 0.000000000 |
| 8 | 0.000000000 |
| 9 | 0.000000000 |
| 10 | 0.000000000 |
| 11 | 0.000000000 |
| 12 | 0.000000000 |
| 十三 | 0.000000005 |
| 14 | 0.000000124 |
| 15 | 0.000001991 |
| 16 | 0.000022848 |
| 17 | 0.000191281 |
| 18 | 0.001186530 |
| 19 | 0.005519547 |
| 20 | 0.019434593 |
| 21 | 0.052152293 |
| 22 | 0.107159339 |
| 23 | 0.169042497 |
| 24 | 0.204864337 |
| 二十五 | 0.190490321 |
| 二十六 | 0.135436876 |
| 二十七 | 0.073211471 |
| 二十八 | 0.029838199 |
| 二十九 | 0.009063960 |
| 三十 | 0.002020713 |
| 31 | 0.000323888 |
| 三十二 | 0.000036309 |
| 33 | 0.000002742 |
| 三十四 | 0.000000132 |
| 三十五 | 0.000000004 |
| 三十六 | 0.000000000 |
| 三十七 | 0.000000000 |
| 三十八 | 0.000000000 |
| 全部的 | 1.000000000 |
表格顯示,最有可能的結果是 24 個不同的數字,機率為 20.49%。平均值為 24.20656478。
有些江湖騙子會說,玩家應該觀察前九個不同的結果,然後押注,因為他們錯誤地認為這些結果比其他數字更有可能出現。這完全是錯誤的!輪盤和球沒有記憶。在公平的輪盤上,每個數字都有同等的可能性,過去的數字並不重要。