概率 - 骰子
如果您擲 6 個六面標準骰子,擲出六個相同點數的機率是多少?
答案是 6*(1/6) 6 = 6/46,656 = 1/7,776 =~ 0.0001286 。
投擲者平均要投擲幾次才能擲出「7」?我知道每投擲6次就會出現一次7,但考慮到7-11和擲骰子遊戲,再加上投擲者可能多次擲出點數,我認為平均投擲次數可能會高於預期。有沒有這方面的數學參考資料?
每位玩家平均擲骰次數為8.525510次。要了解擲骰次數剛好為2到200次的機率,請參閱我的「擲骰子生存機率」頁面。
在 100,000 次擲骰子(擲骰子/不通過線)中,連續輸掉 2 次、3 次、4 次、5 次、6 次、7 次、8 次或 9 次 DP 賭注的幾率(和頻率)是多少。
我的擲骰子附錄顯示如何計算任一次下注的賠率。你會看到,不及格投注的輸掉機率是 2928/5940。連續輸掉 n 次投注的機率是 (2928/5940) n 。 100,000 次投注中剛好輸掉 n 次的機率可以近似為 100,000 * (2928/5940) n+2 。
一次擲六顆骰子擲出相同數字的機率是多少?
用六個骰子擲出六個相同數字的機率是 6*(1/6) 6 =1/7776 =~ 0.01286%。
你擲一對骰子28次不擲出7的機率是多少?你是怎麼算出來的?恭喜你的網站,太棒了。
謝謝你的讚美。我猜你的意思是,擲一對骰子28次都不擲出7的機率是多少。任何擲出7的機率是5/6。28次擲出7的機率是(5/6) /28 = 0.006066,大約是1/165。
想問一下關於東方骰子遊戲的問題。遊戲中玩家需要猜測骰子的哪一面朝上。玩家先在1、2、3、4、5、6上投注(類似輪盤賭),然後「莊家」會同時擲3個骰子。如果所選數字出現一次(在3個骰子中的任何一個上),賠率為1:1;如果所選數字出現兩次,則賠率為2:1;如果所選數字同時出現在3個骰子上,則賠率為3:1。由於玩家可以任意下注,那麼最佳下注數是多少? (假設我所有賭注的金額相同)
巫師先生,擲四個骰子時擲出兩對的機率是多少?
可能的組合有 (6,2)=15 種不同的對子組合。擲骰子擲出任一特定的兩對子,有 (4,2)=6 種組合方式。擲四個骰子,有 6^4=1296 種方法。因此機率為 90/1296=6.9444%。
如果我擲一個骰子,擲出六點的機率是 1/6。如果我擲兩顆骰子,其中一個擲出六點的機率會增加,還是維持在 1/6?
如果你擲了 x 個骰子,那麼至少擲出一個 6 的機率是 1-(5/6) 2 。如果擲的是兩顆骰子,那麼這個機率就是 30.56%。
使用 6 個骰子擲出 3 個 1 有多少種不同的方法?
首先,有 (6,3)=20 種組合方法,可以從 6 個骰子中選出 3 個,作為三個 1。然後,其他 3 個骰子可以分別代表 5 個數字。所以,總共有 20×5 3 =2500 種組合方法。擲出所有骰子的方法總數為 6 6 =46,656 種,因此擲出三個 1 的機率為 2500/46656=0.0536。有關組合函數的協助,請參閱我在撲克部分提供的機率。
三個骰子同時擲,任一個骰子點數1的機率是多少?我的理解應該是50%(1/6+1/6+1/6=1/2 -->50%),但你的賠率表顯示的是34.72%。請幫忙。
用三個骰子擲出剛好一個「1」的機率是 3*(5/6) 2 *(1/6) = 75/216 = 34.72%。
拋 4 顆骰子時擲出「對子」的機率是多少?
這對數字可以是 6 個數字中的任一個。另外兩個單數可以是其他五個數字中的任一個。因此,已經有 6*combin(5,2)=60 種組合。有 combin(4,2)=6 種骰子組合可以出現這對數字。這兩個單數可以用兩種方式排列。因此,共有 60*12=720 種投擲方法。所有投擲方法總數為 6 4 =1296。因此,機率為 720/1296 =~ 55.56%。
我朋友開了一家酒吧,他有一種“每日奶昔”,特百惠容器裡裝著十顆骰子,請問一下,一次搖晃就能匹配十顆骰子中的八顆的概率是多少?謝謝您的寶貴時間。
擲 10 個骰子,剛好有 8 個數字相同的機率為 6*combin(10,8)*(1/6) 8 *(5/6) 2 = 1/8957.952。至少有 8 個數字相同的機率為 6*[combin(10,8)*(1/6) 8 *(5/6) 2 + combin(10,9)*(1/6) 9 *(5/6) + (1/6) 10 ] = 1/8569.469。
我最近在玩西洋雙陸棋時,連續四次擲出雙六。這種情況再次發生的機率是多少?
每次新擲骰子時,接下來四次擲骰子均為雙六的機率為 (1/36) 4 = 1/1679616。
一次擲 5 顆骰子得到順子的機率是多少?
有兩種可能的跨度:1 到 5 和 2 到 6。每種跨度有 5!=120 種排列方式。擲五顆骰子共有 6 *5 = 7776 種方法。因此機率為 2*120/7776 = 3.09%。在玩 Yahtzee 時,當我把 0 標記為大順子後,這個機率似乎高了很多。
一個面公平的骰子擲了30次。數字1出現的預期次數是多少?數字1出現的機率是多少?
預期的 1 的數量是 30*(1/6) = 5。剛好出現 5 個 1 的機率是 combin(30,5)*(1/6) 5 *(5/6) 25 = 19.21%。
如果我有任意數量的骰子,那麼如果我擲出所有骰子,至少有一個骰子落在 1 上的機率是多少?
骰子點數不全為 1 的機率是 (5/6) n 。因此,至少有一個點數為 1 的機率是 1-(5/6) n 。我們以五顆骰子為例。答案是 1-(5/6) 5 = 59.81%。
如果我擲 36 顆骰子,至少擲出一個六點的機率是多少?
1-(5/6) 36 = 99.86%
如果我繼續擲骰子,每次都將六點全部去掉,那麼我如何預測特定次數的擲骰子後剩餘的理論骰子數量?
每次投擲,預期剩餘骰子數量為 5/6。因此,投擲 n 次後剩餘骰子數量的預期值為 36*(5/6) n 。例如,投擲 10 次後,平均剩餘骰子數量為 5.81 個。
如果我擲三個骰子,至少有兩個數字相同的機率是多少?
所有數字不同的機率是 (5/6)*(4/6)=20/36。因此,至少有兩個數字相同的機率是 1-(20/36) = 16/36 = 44.44%。
如果兩個人擲一對骰子,擲出相同數字的機率是多少?有沒有公式可以計算?
是的。你只需計算從 2 到 12 的所有數字,並確定每個數字擲出兩次的機率。所以答案是 (1/36) 2 + (2/36) 2 + (3/36) 2 + (4/36) 2 + (5/36) 2 + (6/36) 2 + (5/36) 2 + (4/36) 2 + (3/36) 2 + (5/36) 2 + (4/36) 2 + (3/36) 2 + (5/36) 2 + (4/36) 2 + (3/36) 2 + (2/36)。
我最近參加了一個醫院慶祝活動。獎品是,如果一次擲出7個骰子,出現7個六,就能贏得一輛新車。每次1英鎊。這機率一定很高,但究竟有多高呢?
用七顆骰子擲出七個六的機率是 (1/6) 7 = 279,936 分之一。所以,這輛車的價值必須達到 279,936 英鎊或更高,這才是一個很好的賭注。即使是普通的勞斯萊斯也不值這麼多錢,所以我認為這是一場糟糕的賭注。
[Bluejay 補充說:呃,是的,但我覺得重點是這是為了慈善事業。哪個更有趣:捐 1 英鎊給慈善機構,除了幫忙的快感什麼也得不到,還是捐 1 英鎊,除了快感之外,還有贏得一輛車的幾率? ]
擲五顆骰子,得到 5 條、4 條、3 條、葫蘆、2 對、一對、順子和零的機率是多少?
- 五張同點牌:6/6 5 = 0.08%(顯而易見)
- 四張同點牌:5*6*5 = 1.93%(單張的 5 種可能位置 * 四張同點牌的 6 種等級 * 單張的 5 種等級)。
- 葫蘆:combin(5,3)*6*5/6 5 = 3.86%(combin(5,3) 三條的位置 * 三條的 6 個等級 * 對子的 2 個等級)。
- 三張同點牌:COMBIN(5,3)*COMBIN(2,1)*6*COMBIN(5,2) / 6 5 = 15.43%。 (combin(5,3) 三張同點牌的位置 * combin(2,1) 較大單張牌的位置 * 三張同點牌的 6 個等級 * combin(5,2) 兩張單張牌的等級。)
- 兩對:COMBIN(5,2)*COMBIN(3,2)*COMBIN(6,2)*4 / 6 5 = 23.15%(較高對的組合(5,2) 位置 * 較低對的組合(3,2) 位置 * 兩對的組合(6,4) 位置 * 較低對的組合(3,2) 位置 * 兩對的組合(6,4) 排名 * 排名單對的 4 排名)。
- 配對:COMBIN(5,2)*fact(3)*6*combin(5,3) / 6 5 = 46.30%(配對的 combin(5,2) 位置 * 三個單例的 fact(3) 位置 * 配對的 6 個等級 * 單一的 combin(5,3) 等級)。
- 直線:2*fact(5) / 6 5 = 3.09%(直線的2個跨距{1-5或2-6} * fact(5) 方式排列順序)。
- 無:((COMBIN(6,5)-2)*FACT(5)) / 6 5 = 6.17%(combin(6,5) 種方法從六個等級中選擇五個等級,減去 2 個直線等級,* fact(5) 種方法來排列順序。
你好,巫師,我想知道你能不能回答這個問題。在17世紀法國流行的一種賭博遊戲中,玩家會擲一對骰子24次。如果至少有一次擲出雙六,他就贏了。當時關於獲勝機率是高於還是低於50%有爭議。你能幫我嗎?
當然,這很簡單。 24 次投擲中至少擲出一個 12 的機率是 1-(35/36) 24 = 49.14%。因此,押注不擲 12 的賠率更高。這是一個明智的選擇,因為 24 次投擲中擲出 12 的預期次數是 2/3。然而,這並不意味著擲出 12 的機率就是 2/3,因為有時擲出 12 的次數會不只一次,而且押注 12 的玩家在擲出第一個 12 之後不會再贏任何額外的 12。假設每次投擲的獲勝機率為 p,投擲次數為 n,至少贏一次的機率為 w,那麼用 p 和 w 來解 n 可得…
w=1-(1-p) n
1-w = (1-p) n
log(1-w) = log((1-p) n )
log(1-w) = n*log(1-p)
n= log(1-w)/log(1-p)
所以在你的例子中,n = log(1-.5) / log(1-(1/36)) = log(0.5) / log(35/36) = 24.6051。所以,如果24.6次投擲的成功機率是50%,那麼24次投擲的成功機率一定會略低。
用六顆骰子連續六次擲出 1、2、3、4、5、6 的機率是多少?
一次擲六個骰子,擲出 123456 的機率可以表示為:prob(第二個骰子與第一個骰子不符) * prob(第三個骰子與第一個或第二個骰子都不匹配) * ... = 1*(5/6)*(4/6)*(3/6)*(2/6)*(1/65) = 0.0023。因此,連續六次擲出 123456 的機率為 0.015432 6 = 74,037,208,411 分之 1。
如果我擲一個骰子 6 次,那麼剛好 4 次出現「2」的機率是多少?
合併(6,2)*(1/6) 4 *(5/6) 2 = 0.008037551。
如果允許你保留擲出的最高的三個骰子,那麼用 3、4 和 5 個骰子擲出 13 或更大的機率是多少?
機率如下:
3個骰子:25.93%
4個骰子:48.77%
5個骰子:66.13%。
假設我們擲三個公平的六面骰。假設三個骰子點數總和為 12,那麼第一個骰子點數為 4 的條件機率是多少?
給定B,A的機率等於A和B的機率除以B的機率。在這種情況下,第一個骰子擲出4,然後另外兩個骰子擲出總點數8的機率是(1/6)*(5/36) = 5/216。3個骰子擲出總點數12的機率是25/216,正如我的骰寶部分所示。所以答案是(5/216)/(25/216) = 5/25 = 20%。
在最近的一次程式設計練習中,我和其他學生被要求用程式碼描述一個六面骰子,然後用我們的骰子玩一個簡單的遊戲。遊戲的目標是擲骰子,直到擲出點數總和剛好達到 100。任何使點數超過 100 的點數都不會被添加,而只是被添加到統計數據中。很快,我們確定,達到 100 所需的最少擲骰次數是 17 次。然而,計算這種情況發生的機率卻一直難以捉摸。計算特定擲骰順序的機率相當簡單,但如何將非特定的擲骰順序以及在 17 次擲骰中達到 100 的不同方式(16*6 + 1*4 和 15*6 + 2*5)結合起來呢?
您提到的兩種方法是擲 17 次總共擲出 100 的唯一方法。擲 16 個六和一個四的機率是 17*(1/6) 17 。 4 有 17 種可能的位置,每種序列的機率為 (1/6)*(1/6)*...*(1/6),共 17 項。擲出 15 個六和 2 個五的方法數為(17,2) = 136。因此,擲出 15 個六和 2 個五的機率是 136*(1/6) 17 。因此,總機率為 (17+136)*(1/6) 17 。 = 1/110,631,761,077。
有3個骰子,其中2個是真正的六面骰子,1個是所有面都是6的骰子。所有骰子都在我的口袋裡。我隨機拿出一個骰子擲了出去。結果是6。請問這個骰子是真正的六面骰子的機率是多少?
設 A = 選擇正常骰子
設 B = 用隨機選取的骰子擲出 6
答案 = Pr(A 已知 B) = Pr(A 和 B)/pr(B) = ((2/3)*(1/6))/((2/3)*(1/6)+(1/3)*1) = (2/18)/((2/18)+(6/18)) = 1/4。
如果只能擲一次六顆骰子,那麼以任意順序擲出 6、6、6、6、1 和 4 的機率是多少?
有 6!/(4!*1!*1!) = 30 種方法可以按任意順序排列這些數字。換一種理解,有 6 個位置可以放置 1,剩下 5 個位置可以放置 4,所以 6*5=30。以這個順序得到 666614 的機率是1/6 = 1/46656。將此機率乘以 30,得出 30/46656 = 0.0643%,即 1/1552.2。
我理解的事件「等待時間」是該事件機率的倒數。我感興趣的是計算用一個骰子擲出連續2的等待時間。在模擬中,我平均擲出42次。我該如何將其與擲出連續2的機率連結起來?
對於單一事件,如果機率為 p,則平均等待時間為 1/p,這的確沒錯。然而,對於連續事件,情況會變得更加複雜。設 x 表示最後一次擲出的結果不是 2 的狀態。這也是初始狀態。設 y 表示最後一次擲出的結果為 2 的狀態。第一次擲出結果後,我們有 5/6 的機率仍處於狀態 x,有 1/6 的機率處於狀態 y。設 Ex(x) 表示從狀態 x 開始的擲骰次數的預期,Ex(y) 表示從狀態 y 開始的擲骰次數的預期。那麼…
Ex(x) = 1 + (5/6)*ex(x) + (1/6)*ex(y),且
Ex(y) = 1 + (5/6)*ex(x)
求解這兩個方程式...
Ex(x) = 1 + (5/6)*ex(x) + (1/6)*( 1 + (5/6)*Ex(x))
Ex(x) = 7/6 + (35/36)*Ex(x)
(1/36)*Ex(x)= 7/6
例如(x)= 36 *(7/6)= 42
因此連續兩次擲出 2 的平均等待時間為 42 次。
我遇到了相同類型的問題,只有預期翻轉才能得到兩次正面,在我的數學問題網站上,請參閱問題 128。
你能告訴我用兩個、三個和四個骰子擲出兩個相同數字的機率嗎?我想知道,一次需要擲多少骰子才能讓賠率站在擲骰子的人這邊。 (哪個數字翻倍都無所謂。)
根據擲骰次數,出現至少一個數字多次的機率如下:
一對或多對的機率
| 麵包捲 | 可能性 |
| 2卷 | 16.67% |
| 3卷 | 44.44% |
| 4卷 | 72.22% |
| 5卷 | 90.74% |
| 6卷 | 98.46% |
擲20個骰子,得到大於100的點數的機率是多少?
我開始使用常態近似來解決這個問題,但超過100個點的機率太低,方法不夠準確。因此,我進行了825萬次試驗的隨機模擬,其中101個點或以上的試驗次數為127次。因此,機率約為65,000分之一。
巫師,您能描述一下加州超級樂透(California SuperLotto Plus,4140萬分之一)的中獎機率嗎?具體來說,是指連續擲出7或11的次數嗎?我以前在哪裡聽過。大多數人無法理解彩票的中獎機率。但是,擲骰子——他們卻能理解。
設答案為 n。擲出 7 或 11 的機率為 8/36。求解 n:
(8/36) n = 1/41,400,000
log((8/36) n ) = log(1/41,400,000)
n × log(8/36) = log(1/41,400,000)
n = log(1/41,400,000)/log(8/36)
n = -7.617 / -0.65321
n = 11.6608
所以,超級樂透中獎的機率,相當於連續11.66次擲7或11的機率。對於那些無法理解「部分投擲」的人,我建議將其理解為連續擲出11到12次的機率。
我們兩個工人之間發生了爭執。街上有個酒吧,每天搖一次骰子。就是說你必須一次擲五個骰子,而且五個骰子點數必須相同,“就像玩快艇骰子一樣”,但是酒吧給你三次機會。但你必須三次都把骰子撿起來。所以問題是,一次擲骰子成功和三次擲骰子成功的可能性分別是多少。謝謝!如果你之前已經回答過這個問題,很抱歉,我找不到了。
一次擲出五條的機率是 6*(1/6) 5 = 1/1,296。這是因為五個有六種不同的形式(一到六),而每次擲出該數字的機率是 (1/6)。擲不出五條的機率是 1-(1/1,296)=1,295/1,296。三次擲不出三條的機率是 (1,295/1,296) 3 =99.77%。因此,三次擲出至少一張五條的機率是 100%-99.77% = 0.23%。
為了獲得無偏向的 6 面骰上每種可能結果中的至少一種,預計需要投擲多少次?
如果某件事的機率是 p,那麼平均需要 1/p 次嘗試才能第一次發生。顯然,第一次擲骰子時你會劃掉一個數字。接下來擲出其他五個數字的機率是 5/6。因此,平均需要 1/(5/6)=6/5=1.2 次才能發生這種情況。依照這個推理,預期擲骰子次數為 (6/6)+(6/5)+(6/4)+(6/3)+(6/2)+(6/1) = 14.7。
擲 5 個平衡骰子時,得到總數 12 的經典機率是多少?
希望您滿意,我剛剛添加了一個新版塊,專門解答類似這樣的問題,適用於 1 到 25 個骰子。如五骰表所示,擲出 12 的機率是 0.039223251028807。
如果重複擲兩顆骰子,直到發生以下任一事件,那麼哪個事件更有可能先發生:
- 擲出的總數為六和八,順序不限,允許重複。
- 總共擲兩次,結果都是七。
有人跟我打賭,6 和 8 會先出現。我答應了,因為 7 是最有可能的數字。然而,我一次又一次地輸掉了 2500 美元。這個機率到底有多大?
恐怕你這次下注是贏了。先擲出兩個7,再擲出6和8的機率是45.44%。以下是所有可能的結果。第一列是與下注結果相關的擲骰順序,忽略所有其他結果。
兩個七,然後是六和八的賭注
| 相關卷 | 可能性 | 公式 | 結果 |
| 6,8 | 0.142045 | (5/16)*(5/11) | 失去 |
| 8,6 | 0.142045 | (5/16)*(5/11) | 失去 |
| 6,7,8 | 0.077479 | (5/16)*(6/11)*(5/11) | 失去 |
| 7,6,8 | 0.053267 | (6/16)*(5/16)*(5/11) | 失去 |
| 8,7,6 | 0.077479 | (5/16)*(6/11)*(5/11) | 失去 |
| 7,8,6 | 0.053267 | (6/16)*(5/16)*(5/11) | 失去 |
| 7,7 | 0.140625 | (6/16)*(6/16) | 贏 |
| 6,7,7 | 0.092975 | (5/16)*(6/11)*(6/11) | 贏 |
| 8,7,7 | 0.092975 | (5/16)*(6/11)*(6/11) | 贏 |
| 7,6,7 | 0.06392 | (6/16)*(5/16)*(6/11) | 贏 |
| 7,8,7 | 0.06392 | (6/16)*(5/16)*(6/11) | 贏 |
基本上,6 和 8 是更好的選擇,因為您可以按任意順序擊中這些數字:6 然後 8,或 8 然後 6。如果有兩個 7,則只有一個順序,即一個 7 然後另一個 7。
請問兩題:1)用(6)個六面骰子,一次擲出 6,6,6,6,6,6 的機率是多少? 2)用(6)個六面骰子,一次擲出 1,2,3,4,5,6 的機率是多少?謝謝!這太讓我頭痛了!
六個六的機率是 (1/6) 6 = 1/46656。用六個骰子擲出 1,2,3,4,5,6 的機率是 6 ! /6 6 = 1/64.8
如果擲骰子十次,出現任意給定數字超過一次的機率是多少?
1-(5/6) 10-10 ×(1/6)×(5/6) 9 =51.55%。
在一個名為「逃稅與逃稅」的遊戲中,玩家擲一對骰子。如果擲出的點數為7、11或12,玩家將被審計;如果擲出的點數為其他點數,玩家可以逃稅。如果玩家擲出5次這樣的骰子,他逃稅的機率是多少?
擲出 7、11 或 12 的機率是 (6+2+1)/36 = 9/36 = 1/4。請參閱我關於骰子機率基礎的部分,以了解我是如何得出這個數字的。擲出其他點數的機率是 3/4。擲 5 次未擲出 7、11 或 12 的機率是 (3/4) 5 = 23.73%。
你需要擲多少次骰子,才有可能至少擲出 1、2、3、4、5 和 6 一次?有什麼辦法可以推廣到 n 面骰嗎?
雖說你沒問,但我先來談談平均值。對於一個六面骰子,至少擲出每個面一次的預期次數是 (6/6) + (6/5) + (6/4) + (6/3) + (6/2) + (6/1) = 14.7。對於一個 n 面骰子,預期次數是 (n/n) + (n/(n-1)) + (n/(n-2)) + ... + n。所需擲骰子的中位數是 13。擲出 13 次或更少的機率是 51.4%,擲出 13 次或更多的機率是 56.21%。
我知道你對骰子控制持懷疑態度。我已經練習了三個月的骰子設定和控制投擲了。隨機投擲655次,擲出78個7的機率是多少?謝謝你的幫忙 :)
對於大量投擲,我們可以使用高斯曲線近似。 655次投擲中,預期出現7的次數為655 × (1/6) = 109.1667。變異數為655 × (1/6) × (5/6) = 90.9722。標準差為sqr(90.9722) = 9.5379。您的78次投擲結果比預期值低109.1667 − 78 = 31.1667。這相當於(31.1667 - 0.5)/9.5379 = 3.22個標準差。低於預期值3.22個或更多標準差的機率為0.000641,即1/1560。我在Excel中使用公式normsdist(-3.22)得出了這個數字。
這是關於擲骰子遊戲的骰子控制。您之前討論過史丹佛黃實驗,其中提到:「賭注的條件是,精準投擲者在500次擲骰子中能否擲出少於79.5個7。在隨機遊戲中,預期數字是83.33。在500次隨機擲骰子中擲出79個或更少7的機率是32.66%…在500個隨機擲骰子中擲出79個或更少7的機率是32.66%…在50014%中擲出14%。
我對這個賭注的疑問是,14.41% 仍然不是「統計上顯著的」 [即 p < 0.05],這通常被認為意味著距離平均值大於兩個標準差 - 或者事件在系列的任一端隨機發生的機率小於*綜合* 5%。
在您可以說結果完全隨機(即結果具有統計意義)的可能性小於 2.5% 之前,需要在 500 次投擲中投出多少個“7”?
非常感謝,順便說一句,您的網站絕對是我發現的有關賭博賠率和概率的最佳網站......繼續努力! ! !
謝謝你的讚美。你不應該說投擲結果非隨機的機率是p。應該這樣表述:一場隨機遊戲產生這種結果的機率是p。沒人指望500次投擲就能證明或反駁任何事情。我並沒有把79.5個7的點數定為79.5,但我懷疑這個點數是否具有統計意義;相反,我懷疑這是一個雙方都會同意下注的點。
2.5% 的顯著水準是與預期值相差 1.96 個標準差。這可以在 Excel 中使用公式 =normsinv(0.025) 計算得出。 500 次投擲的標準差為 sqr(500*(1/6)*(5/6)) = 8.333。因此,1.96 個標準差等於 1.96 * 8.333 = 16.333 次,比預期值低。 500 次投擲中出現七的預期次數為 500*(1/6) = 83.333。因此,比預期值低 1.96 個標準差等於 83.333 − 16.333 = 67。使用二項分佈檢驗,出現 67 次或更少七的準確機率為 2.627%。
贏得 Yahtzee 需要預計擲幾次?
假設玩家總是持有出現次數最多的數字,則平均值為11.09。下表顯示了在8,260萬次隨機模擬試驗中,擲骰次數的分佈。
骰子實驗
| 麵包捲 | 發生 | 可能性 |
| 1 | 63908 | 0.00077371 |
| 2 | 977954 | 0.0118396 |
| 3 | 2758635 | 0.0333975 |
| 4 | 4504806 | 0.0545376 |
| 5 | 5776444 | 0.0699327 |
| 6 | 6491538 | 0.0785901 |
| 7 | 6727992 | 0.0814527 |
| 8 | 6601612 | 0.0799227 |
| 9 | 6246388 | 0.0756221 |
| 10 | 5741778 | 0.0695131 |
| 11 | 5174553 | 0.0626459 |
| 12 | 4591986 | 0.0555931 |
| 十三 | 4022755 | 0.0487016 |
| 14 | 3492745 | 0.042285 |
| 15 | 3008766 | 0.0364257 |
| 16 | 2577969 | 0.0312103 |
| 17 | 2193272 | 0.0265529 |
| 18 | 1864107 | 0.0225679 |
| 19 | 1575763 | 0.019077 |
| 20 | 1329971 | 0.0161013 |
| 21 | 1118788 | 0.0135446 |
| 22 | 940519 | 0.0113864 |
| 23 | 791107 | 0.00957757 |
| 24 | 661672 | 0.00801056 |
| 二十五 | 554937 | 0.00671837 |
| 二十六 | 463901 | 0.00561624 |
| 二十七 | 387339 | 0.00468933 |
| 二十八 | 324079 | 0.00392347 |
| 二十九 | 271321 | 0.00328476 |
| 三十 | 225978 | 0.00273581 |
| 31 | 189012 | 0.00228828 |
| 三十二 | 157709 | 0.00190931 |
| 33 | 131845 | 0.00159619 |
| 三十四 | 109592 | 0.00132678 |
| 三十五 | 91327 | 0.00110565 |
| 三十六 | 76216 | 0.00092271 |
| 三十七 | 63433 | 0.00076795 |
| 三十八 | 52786 | 0.00063906 |
| 三十九 | 44122 | 0.00053417 |
| 40 | 36785 | 0.00044534 |
| 41 | 30834 | 0.00037329 |
| 四十二 | 25494 | 0.00030864 |
| 43 | 21170 | 0.0002563 |
| 四十四 | 17767 | 0.0002151 |
| 45 | 14657 | 0.00017745 |
| 46 | 12410 | 0.00015024 |
| 四十七 | 10299 | 0.00012469 |
| 四十八 | 8666 | 0.00010492 |
| 49 | 7355 | 0.00008904 |
| 50 | 5901 | 0.00007144 |
| 51 | 5017 | 0.00006074 |
| 52 | 4227 | 0.00005117 |
| 53 | 3452 | 0.00004179 |
| 54 | 2888 | 0.00003496 |
| 55 | 2470 | 0.0000299 |
| 56 | 2012 | 0.00002436 |
| 57 | 1626 | 0.00001969 |
| 58 | 1391 | 0.00001684 |
| 59 | 1135 | 0.00001374 |
| 60 | 924 | 0.00001119 |
| 61 | 840 | 0.00001017 |
| 62 | 694 | 0.0000084 |
| 63 | 534 | 0.00000646 |
| 64 | 498 | 0.00000603 |
| 65 | 372 | 0.0000045 |
| 66 | 316 | 0.00000383 |
| 67 | 286 | 0.00000346 |
| 68 | 224 | 0.00000271 |
| 69 | 197 | 0.00000238 |
| 70 | 160 | 0.00000194 |
| 71 | 125 | 0.00000151 |
| 72 | 86 | 0.00000104 |
| 73 | 79 | 0.00000096 |
| 74 | 94 | 0.00000114 |
| 75 | 70 | 0.00000085 |
| 76 | 64 | 0.00000077 |
| 77 | 三十八 | 0.00000046 |
| 78 | 四十二 | 0.00000051 |
| 79 | 二十七 | 0.00000033 |
| 80 | 33 | 0.0000004 |
| 81 | 16 | 0.00000019 |
| 82 | 18 | 0.00000022 |
| 83 | 19 | 0.00000023 |
| 84 | 14 | 0.00000017 |
| 85 | 6 | 0.00000007 |
| 86 | 4 | 0.00000005 |
| 87 | 9 | 0.00000011 |
| 88 | 4 | 0.00000005 |
| 89 | 5 | 0.00000006 |
| 90 | 5 | 0.00000006 |
| 91 | 1 | 0.00000001 |
| 92 | 6 | 0.00000007 |
| 93 | 1 | 0.00000001 |
| 94 | 3 | 0.00000004 |
| 95 | 1 | 0.00000001 |
| 96 | 1 | 0.00000001 |
| 97 | 2 | 0.00000002 |
| 102 | 1 | 0.00000001 |
| 全部的 | 82600000 | 1 |
假設一個基於擲骰子的遊戲。如果骰子擲出 1,玩家輸掉 1 美元,遊戲結束。如果骰子擲出其他任何點數,玩家贏取 1 美元。此時,玩家可以選擇放棄,也可以選擇退出。玩家可以繼續遊戲,每次下注加倍,直到輸掉或退出。最佳策略是什麼?
僅從最大化期望值的角度來說,玩家應該永遠玩下去。雖然玩家最終輸掉的機率是1,但在任何給定的決策點,期望值總是傾向於再次玩下去。這似乎是一個悖論。答案在於,有些事件的機率是1,但仍然可能不會發生。例如,如果你向0到10的數字線投擲飛鏢,沒有剛好擊中π的機率是1,但這仍然有可能發生。
然而,從實際角度來看,存在一個臨界點。這是因為金錢帶來的幸福感並非與金錢的多寡成正比。雖然人們普遍認為金錢越多,幸福感越強,但你越富有,每一美元帶來的幸福感就越少。
我認為回答這個問題的一個好方法是運用凱利準則。根據凱利準則,玩家在做每個決定時都應該以最大化下注後資金的預期對數為目標。簡而言之(我省略了很多數學運算),玩家應該不斷加倍,直到下注金額超過其總財富的 96.5948%。財富應該定義為贏得的金額加上玩家在第一次下注前擁有的資金總和。例如,如果玩家的起始資金為 100,000 美元,他應該不斷加倍,直到贏得 4,194,304 美元。此時,玩家的總財富將達到 4,294,304 美元。他將被要求下注 4,194,304/4,294,304 = 其總財富的 96.67%,這大於 96.5948% 的停止點,所以他應該退出。
玩家 A 和 B 擲一對骰子。如果玩家 A 在 B 擲出 7 之前擲出 6,則 A 獲勝;如果 B 在 A 擲出 6 之前擲出 7,則 B 獲勝。如果由 A 先擲,則表示 A 獲勝的機率為 30/61。
假設這個問題的答案為 p。擲出總點數 6 的機率是 5/36,擲出總點數 7 的機率是 6/36。如果您不明白為什麼,請參閱我關於骰子機率基礎的部分。我們可以將 p 定義為:
p = Prob(第一次擲出 6) + Prob(第一次擲出未出現 6)*Prob(第二次擲出未出現 7)*p。
這是因為,如果前兩次擲骰子後沒有一個玩家獲勝,遊戲就會回到原始狀態,玩家 A 獲勝的機率保持不變。
因此,我們有:
p = (5/36) + (31/36)×(30/36)×p
p = 5/36 + (930/1296)×p
p * (1-(930/1296)) = 5/36。
p * (366/1296) = 5/36
p = (5/36)×(1296/366) = 30/61。
擲 n 個六面且點數相同的骰子有幾種方法?如上所述,骰子點數相同,因此,例如,如果擲 5 個骰子,1-1-3-5-6 和 1-6-5-1-3 會被視為相同的結果。如果擲 2 個骰子,很容易確定答案是 21,但我找不到一個優雅且通用的解決方案。
答案可以表示為 combin(n+5,n) = (n+5)!/(120×n!)。以下是 1 到 20 個骰子的答案。
非唯一骰子組合
| 骰子 | 組合 |
| 1 | 6 |
| 2 | 21 |
| 3 | 56 |
| 4 | 126 |
| 5 | 252 |
| 6 | 462 |
| 7 | 792 |
| 8 | 1287 |
| 9 | 2002 |
| 10 | 3003 |
| 11 | 4368 |
| 12 | 6188 |
| 十三 | 8568 |
| 14 | 11628 |
| 15 | 15504 |
| 16 | 20349 |
| 17 | 26334 |
| 18 | 33649 |
| 19 | 42504 |
| 20 | 53130 |
| 21 | 65780 |
| 22 | 80730 |
| 23 | 98280 |
感謝《應用組合學》的作者艾倫‧塔克 (Alan Tucker)。
你能計算擲骰子時兩個數字接連出現的機率嗎?也就是說,連續出現兩個4、兩個6或兩個7的機率是多少?我知道過去無法預測未來,但有沒有辦法計算出7/36 x 7/36連續出現的機率?希望你理解得通。
當然。那就是 Pr(2) 2 + Pr(3) 2 + ... + Pr(12) 2 = (1/36) 2 + (2/36) 2 + (3/36) 2 + (4/36) 2 + (5/36) 2 + (6/36) 2 + (5/36) 2 + (5/36) 2 + (6/36) 2 + (5/36) 2 + 24 +/ 36 (1/36) 2 = 11.27%。
在連續 180 次擲骰子中,我預計會看到以下結果多少次:
連續兩個七?
連續三個七?
連續四個七?
感謝您的時間:-)。
我想不出任何有用的理由來了解這些信息,但我經常被問到這種問題,所以我會遷就你。
從第一次擲骰開始,或從最後一次擲骰結束,得到一個指定的7的序列會稍微容易一些,因為這個序列有界於某一側。具體來說,從第一次擲骰開始,或從最後一次擲骰結束,得到s個7的序列的機率是(1/6) s × (5/6)。 5/6項是因為你必須在序列的開口端得到一個非7的點數。
在序列中間任一點開始 s 個 7 的序列的機率是 (1/6) s × (5/6) 2 。我們將 5/6 平方,因為玩家必須在序列的兩端都拿到非 7 的點數。
如果擲出 r 次,則內側序列有 2 個位置,連續 n 個 7 有 rn-1 個位置。將這些公式代入表格中,即可得出連續 7 的預期次數,範圍從 1 到 10。 「內側」列為 2*(5/6)*(1/6) r ,「外側」列為 (179-r)*(5/6) 2 *(1/6) r ,其中 r 是連續 7 的數量。因此,我們預期連續出現兩個 7 的機率為 3.46,連續出現三個 7 的機率為 0.57,連續出現四個 7 的機率為 0.10。
180 次投擲中預期出現 7 的次數
| 跑步 | 裡面 | 外部 | 全部的 |
| 1 | 0.277778 | 20.601852 | 20.87963 |
| 2 | 0.046296 | 3.414352 | 3.460648 |
| 3 | 0.007716 | 0.565844 | 0.57356 |
| 4 | 0.001286 | 0.093771 | 0.095057 |
| 5 | 0.000214 | 0.015539 | 0.015754 |
| 6 | 0.000036 | 0.002575 | 0.002611 |
| 7 | 0.000006 | 0.000427 | 0.000433 |
| 8 | 0.000001 | 0.000071 | 0.000072 |
| 9 | 0 | 0.000012 | 0.000012 |
| 10 | 0 | 0.000002 | 0.000002 |
擲兩顆骰子,直到總數為 12 或連續兩次總數為 7。首先擲出 12 的機率是多少?
答案和解決方案可以在我的配套網站mathproblems.info問題 201 上找到。
我是個桌遊玩家,之前和朋友們討論過非立方體柏拉圖式立體骰子(如果你夠酷的話,那就意味著 d4、d8、d12 和 d20)。他們說只有這些骰子才能真正公平。我則認為,製造出公平的骰子實在太難了。而且,它們只能玩一些類似擲骰子的遊戲,由於額外結果太多,玩起來會變得過於繁瑣。有哪家賭場推出過使用非傳統六面骰子的遊戲嗎?
|
如果你只考慮正多邊形,並希望每個面都有相同的機率,那麼你就只能考慮柏拉圖立體。但是,如果你能取消對正多邊形的要求,那麼你也可以增加13個加泰隆尼亞立體。
回答你的另一個問題,沒有,我從未在賭場裡見過任何遊戲使用立方體以外的骰子。大約十年前,我在大西洋城的一個遊戲展上看到過一款遊戲演示,我記得它用的是菱形三十面體(加泰羅尼亞立體的一種),但我覺得它從未出現在賭場裡。我每年都會在全球遊戲博覽會上看到一款遊戲使用陀螺(類似陀螺),但可惜的是,我也沒在賭場見過。
如果我擲三個六面骰子,擲出順子的機率是多少?擲出三條的機率是多少?
擲三個骰子有 6 3 = 216 種方法。其中六種組合會得到三條(1-1-1 到 6-6-6)。因此,得到三條的機率為 6/216 = 1/36。順子有四種可能的組合(1-2-3 到 4-5-6)。同樣,三個骰子有 3!=6 種組合方式可以形成順子。因此,有 4*6=24 種順子組合。因此,得到順子的機率為 24/216 = 1/9。
擲四個六面骰子,減去最小點數(即 4d6-L)後,平均點數是多少?標準差是多少?
下表顯示了從 3 到 18 的所有可能總數的組合數。
4d6-L 中的組合
| 結果 | 組合 |
| 3 | 1 |
| 4 | 4 |
| 5 | 10 |
| 6 | 21 |
| 7 | 三十八 |
| 8 | 62 |
| 9 | 91 |
| 10 | 122 |
| 11 | 148 |
| 12 | 167 |
| 十三 | 172 |
| 14 | 160 |
| 15 | 131 |
| 16 | 94 |
| 17 | 54 |
| 18 | 21 |
| 全部的 | 1296 |
平均結果為 12.2446,標準差為 2.8468。
我的問題是基於骰子機率的。我知道擲出 7 有六種方法,擲出 12 有一種方法,但是擲出六個 7 而不是一個 12 的機率是多少?它們是等價的嗎?如果不是,應該在等式中添加多少個 12 才能使結果為等價?
擲出 7 的機率是 1/6,擲出 12 的機率是 1/36。假設擲出的點數為 7 或 12,擲出 7 的機率為 (1/6)/((1/6)+(1/36)) = 6/7。因此,前六次擲出 6 或 12 時,每次都是 6 的機率為 (6/7) 6 = 39.66%。
如果你把問題改寫成在擲出12之前擲出五個6的機率是多少,那麼答案是(6/7) 5 = 46.27%。若擲出四次,答案是(6/7) 4 = 53.98%。所以,在擲出12之前,不存在任何剛好50/50的7。如果你想賭一把,建議你要麼在擲出12之前擲出四個7,要麼在擲出五個7之前擲出一個12。
這個問題是在我的同伴網站Wizard of Vegas的論壇中提出並討論的。
有沒有簡單的方法來計算用 d 個 6 面骰子擲出總數為 t 的機率?
這裡有一個實用技巧,由英國薩默塞特郡的羅伯特·古德漢(Robert Goodhand)提供。首先,在一行中放入六個“1”,兩邊分別圍上五個“0”,如下所示:
單骰子機率
| 骰子總數 | 1 | 2 | 3 | 4 | 5 | 6 | ||||||||||
| 一模一樣 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 |
這表示用一個骰子擲出 1 到 6 的組合數。我知道,這很明顯。不過,請聽我說完。如果是兩個骰子,在底部添加一行,每個格子取上一行與其左側五個格子之和。然後,如果您想繼續,在右側再新增五個虛擬零。這表示擲出總數為 2 到 12 的組合數。
兩骰子的機率
| 骰子總數 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | ||||||||||
| 一模一樣 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 兩顆骰子 | 0 | 0 | 0 | 0 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 5 | 4 | 3 | 2 | 1 | 0 | 0 | 0 | 0 | 0 |
如果擲三個骰子,只需重複即可。這將代表3到18的組合數。
要計算任意給定點數的機率,請用該點數的組合數除以組合總數。如果是三枚骰子,其總和為 216,也可以很容易地計算為 6 的3 次方。例如,三枚骰子擲出總點數 13 的機率為 21/216 = 9.72%。
所以對於 d 號骰子,你需要從 1 號骰子到 d-1 號骰子依序計算。這在任何電子表格中都很容易完成。
需要擲多少次骰子才能有 50/50 的機率擲出至少一個 12 點?
這是機率論史上的經典問題。很多人錯誤地認為答案是 18,因為擲出 12 的機率是 1/36,而 18×(1/36)=50%。然而,依照這個邏輯,擲 36 次得到 12 的機率應該是 100%,這顯然不是。以下是正確答案。設 r 為擲骰次數。擲出非 12 的機率是 35/36。擲 r 次骰子中沒有擲出 12 的機率是 (35/36) r 。因此,我們需要用以下公式解出 r:
(35/36) r = 0.5
對數(35/36) r = 對數(0.5)
r × log(35/36) = log(0.5)
r = log(0.5)/log(35/36)
r = 24.6051
所以沒有一個整數答案。 24次擲骰子擲出12的機率是1-(35/36) 24 = 49.14%。 25次擲骰子擲出12的機率是1-(35/36) 25 = 50.55%。
如果你想押注,比如說你能在25輪擲出12點,或是其他人在24輪中擲不出。無論哪種情況,你都能在均等投注中佔據優勢。
在骰子戰爭中,給定進攻和防守骰子的數量,成功的機率是多少?作為進攻方,哪個比例的預期效益最大?
對於不熟悉遊戲的人來說,進攻方和防守方都會根據戰鬥中各自擁有的軍隊數量,擲1到8個骰子。點數較高的一方獲勝。如果打平,則防守方獲勝。如果進攻方失敗,他仍然可以在發動攻擊的領土上保留一支軍隊。因此,他必須至少擁有兩支軍隊才能進攻,這樣如果他獲勝,一支軍隊可以佔領被征服的領土,另一支軍隊可以留在原地。
下表顯示了根據所有 64 種骰子組合,攻擊者獲勝的機率。
攻擊者獲勝的機率
| 攻擊者 | 後衛 | |||||||
|---|---|---|---|---|---|---|---|---|
| 第1軍 | 2支軍隊 | 3支軍隊 | 4支軍隊 | 5支軍隊 | 6支軍隊 | 7支軍隊 | 8支軍隊 | |
| 2 | 0.837963 | 0.443673 | 0.152006 | 0.035880 | 0.006105 | 0.000766 | 0.000071 | 0.000005 |
| 3 | 0.972994 | 0.778549 | 0.453575 | 0.191701 | 0.060713 | 0.014879 | 0.002890 | 0.000452 |
| 4 | 0.997299 | 0.939236 | 0.742831 | 0.459528 | 0.220442 | 0.083423 | 0.025450 | 0.006379 |
| 5 | 0.999850 | 0.987940 | 0.909347 | 0.718078 | 0.463654 | 0.242449 | 0.103626 | 0.036742 |
| 6 | 0.999996 | 0.998217 | 0.975300 | 0.883953 | 0.699616 | 0.466731 | 0.259984 | 0.121507 |
| 7 | 1.000000 | 0.999801 | 0.994663 | 0.961536 | 0.862377 | 0.685165 | 0.469139 | 0.274376 |
| 8 | 1.000000 | 0.999983 | 0.999069 | 0.989534 | 0.947731 | 0.843874 | 0.673456 | 0.471091 |
下表顯示了攻擊者的預期收益,定義為pr(攻擊者獲勝)*(防禦者骰子)+pr(防禦者獲勝)*(攻擊者骰子-1)。結果顯示,最大的預期收益是以8點進攻,對手以5點進攻。
攻擊者獲勝的淨收益
| 攻擊者 | 後衛 | |||||||
|---|---|---|---|---|---|---|---|---|
| 第1軍 | 2支軍隊 | 3支軍隊 | 4支軍隊 | 5支軍隊 | 6支軍隊 | 7支軍隊 | 8支軍隊 | |
| 2 | 0.675926 | 0.331019 | -0.391976 | -0.820600 | -0.963370 | -0.994638 | -0.999432 | -0.999955 |
| 3 | 0.918982 | 1.114196 | 0.267875 | -0.849794 | -1.575009 | -1.880968 | -1.973990 | -1.995480 |
| 4 | 0.989196 | 1.696180 | 1.456986 | 0.216696 | -1.236464 | -2.249193 | -2.745500 | -2.929831 |
| 5 | 0.999250 | 1.927640 | 2.365429 | 1.744624 | 0.172886 | -1.575510 | -2.860114 | -3.559096 |
| 6 | 0.999976 | 1.987519 | 2.802400 | 2.955577 | 1.996160 | 0.134041 | -1.880192 | -3.420409 |
| 7 | 1.000000 | 1.998408 | 2.951967 | 3.615360 | 3.486147 | 2.221980 | 0.098807 | -2.158736 |
| 8 | 1.000000 | 1.999847 | 2.990690 | 3.884874 | 4.372772 | 3.970362 | 2.428384 | 0.066365 |
擲骰子 n 次,形成 Yahtzee 的機率是多少?
為了方便其他讀者理解,Yahtzee 指的是用五支骰子擲出五條的骰子。在 Yahtzee 遊戲中,玩家可以保留任何一個骰子,然後重新擲出剩餘的骰子。最多可以擲三次。
如果玩家願意,可以重新擲出先前持有的骰子。例如,如果玩家第一次擲出的骰子是 3-3-4-5-6,他手中持有的是 3,第二次擲出的骰子是 3-3-5-5-5,那麼他可以保留 5,並在第三次擲出的骰子上重新擲出 3。
下表列出了1至20次投擲中,相同面數的骰子的最大數量。表格顯示,三次投擲中贏得Yahtzee的機率約為4.6%。
骰子機率
| 麵包捲 | 同面最大骰子 | ||||
|---|---|---|---|---|---|
| 一 | 二 | 三 | 四 | 五 | |
| 1 | 0.092593 | 0.694444 | 0.192901 | 0.019290 | 0.000772 |
| 2 | 0.008573 | 0.450103 | 0.409022 | 0.119670 | 0.012631 |
| 3 | 0.000794 | 0.256011 | 0.452402 | 0.244765 | 0.046029 |
| 4 | 0.000074 | 0.142780 | 0.409140 | 0.347432 | 0.100575 |
| 5 | 0.000007 | 0.079373 | 0.337020 | 0.413093 | 0.170507 |
| 6 | 0.000001 | 0.044101 | 0.263441 | 0.443373 | 0.249085 |
| 7 | 0.000000 | 0.024501 | 0.199279 | 0.445718 | 0.330502 |
| 8 | 0.000000 | 0.013612 | 0.147462 | 0.428488 | 0.410438 |
| 9 | 0.000000 | 0.007562 | 0.107446 | 0.398981 | 0.486011 |
| 10 | 0.000000 | 0.004201 | 0.077416 | 0.362855 | 0.555528 |
| 11 | 0.000000 | 0.002334 | 0.055317 | 0.324175 | 0.618174 |
| 12 | 0.000000 | 0.001297 | 0.039279 | 0.285674 | 0.673750 |
| 十三 | 0.000000 | 0.000720 | 0.027757 | 0.249063 | 0.722460 |
| 14 | 0.000000 | 0.000400 | 0.019543 | 0.215313 | 0.764744 |
| 15 | 0.000000 | 0.000222 | 0.013720 | 0.184883 | 0.801175 |
| 16 | 0.000000 | 0.000124 | 0.009610 | 0.157896 | 0.832371 |
| 17 | 0.000000 | 0.000069 | 0.006719 | 0.134258 | 0.858954 |
| 18 | 0.000000 | 0.000038 | 0.004692 | 0.113753 | 0.881517 |
| 19 | 0.000000 | 0.000021 | 0.003272 | 0.096100 | 0.900607 |
| 20 | 0.000000 | 0.000012 | 0.002280 | 0.080994 | 0.916714 |
這個問題是在我的「拉斯維加斯巫師」論壇中提出並討論的。
我想知道擲一對骰子時,哪個點數會比較大──奇數還是偶數?
答案是50/50。無論擲多少個骰子,結果都是50/50,而不僅僅是兩個。
有點離題了,但我一直覺得奇偶組合下注是替代擲骰子遊戲中令人畏懼的6/8大注的好方法。為了讓賭場更有優勢,以下是我建議的賠率表和分析。
奇數投注
| 事件 | 支付 | 組合 | 可能性 | 返回 |
|---|---|---|---|---|
| 3 或 11 | 1.5 | 4 | 0.111111 | 0.166667 |
| 5或9 | 1 | 8 | 0.222222 | 0.222222 |
| 7 | 0.5 | 6 | 0.166667 | 0.083333 |
| 甚至 | -1 | 18 | 0.500000 | -0.500000 |
| 全部的 | 三十六 | 1.000000 | -0.027778 |
均等投注
| 事件 | 支付 | 組合 | 可能性 | 返回 |
|---|---|---|---|---|
| 2 或 12 | 3 | 2 | 0.055556 | 0.166667 |
| 4 或 10 | 1 | 6 | 0.166667 | 0.166667 |
| 6或8 | 0.5 | 10 | 0.277778 | 0.138889 |
| 奇怪的 | -1 | 18 | 0.500000 | -0.500000 |
| 全部的 | 三十六 | 1.000000 | -0.027778 |
請注意,我對該出版物主張所有權利。
這個問題是在我的「拉斯維加斯巫師」論壇中提出並討論的。
在 Hot Roll 獎勵中,玩家根據兩個骰子的總點數贏得以下數量的硬幣:
- 2 或 12:1000
- 3或11:600
- 4或10:400
- 5或9:300
- 6或8:200
他一直擲到總數為7,獎勵結束。如果第一次擲出7,他將獲得700枚硬幣的安慰獎。每次獎勵平均能贏得多少枚硬幣?
平均擲骰次數與獎勵結束事件的機率相反,後者的機率為1/6,因此玩家平均擲骰六次。然而,最後一次擲骰次數將是七次,因此平均每次獎勵有五次獲勝。
接下來,假設不是七,以下是每個總數的機率:
- 2 或 12:1/30
- 3或11:2/30
- 4或10:3/30
- 5或9:4/30
- 6或8:5/30
因此,假設沒有七點,每次擲骰子的平均勝利是 2*[(1/30)*1000 + (2/30)*600 + (3/30)*400 + (4/30)*300 + (5/30)*200] = 373.33。
安慰獎的金額為(1/6)*700=116.67。
因此,平均獎金贏額為 116.67 + 5×373.33 = 1983.33。
如果玩家輪流擲骰子,並且只有擲骰子的玩家才能根據擲出的點數前進,那麼「詢問巫師」第 179 欄中的骰子問題的答案是什麼?
這是第 179 欄中提出的原始問題:如果重複擲兩個骰子,直到發生以下任一事件,那麼哪個事件更有可能先發生:
- 擲出的總數為六和八,順序不限,允許重複。
- 總共擲兩次,結果都是七。
你的改變是,同一個擲骰子不能同時幫助兩個玩家。相反,他們輪流擲骰子,並且只有擲骰子的玩家可以使用該擲骰子。
答案取決於誰先擲骰子。如果先擲出需要六和八的玩家,那麼他獲勝的機率是 57.487294%。如果先擲出需要兩張七的玩家,那麼先擲出需要六和八的玩家獲勝的機率是 52.671614%。我用一個簡單的馬可夫鏈過程解決了這個問題。
我在Wizard of Vegas論壇上提出並討論了這個問題。
假設你有12個六面骰。你擲它們,然後可以把任何你想棄掉的骰子放在一邊。然後你重新擲出剩下的骰子。兩次擲出12點的機率是多少?
初始擲骰結果有 58 種不同的序列。我辨識每種序列的方法是:先計算骰麵數最多的數字,然後計算骰麵數第二的骰子總數,以此類推。例如,擲出 3,3,3,3,6,6,6,5,5,2 的機率表示為 4-3-2-1。下表列出了每個序列的組合數、擲出該序列的機率、第二次擲出相同點數 12 的機率以及兩者的乘積。對於第二次擲出的機率,我假設玩家持有初始擲骰結果最大的骰子。右下角單元格顯示的總機率為 0.0000037953,相當於 263,486 分之一。
12 骰子問題
| 順序 | 組合 | 可能性 順序 | 條件 可能性 | 全部的 可能性 |
|---|---|---|---|---|
| 12-0-0-0-0-0 | 6 | 0.0000000028 | 1.0000000000 | 0.0000000028 |
| 11-1-0-0-0-0 | 360 | 0.0000001654 | 0.1666666667 | 0.0000000276 |
| 10-2-0-0-0-0 | 1,980 | 0.0000009096 | 0.0277777778 | 0.0000000253 |
| 10-1-1-0-0-0 | 7,920 | 0.0000036384 | 0.0277777778 | 0.0000001011 |
| 9-3-0-0-0-0 | 6,600 | 0.0000030320 | 0.0046296296 | 0.0000000140 |
| 9-2-1-0-0-0 | 79,200 | 0.0000363840 | 0.0046296296 | 0.0000001684 |
| 9-1-1-1-0-0 | 79,200 | 0.0000363840 | 0.0046296296 | 0.0000001684 |
| 8-4-0-0-0-0 | 14,850 | 0.0000068220 | 0.0007716049 | 0.0000000053 |
| 8-3-1-0-0-0 | 237,600 | 0.0001091519 | 0.0007716049 | 0.0000000842 |
| 8-2-2-0-0-0 | 178,200 | 0.0000818639 | 0.0007716049 | 0.0000000632 |
| 8-2-1-1-0-0 | 1,069,200 | 0.0004911837 | 0.0007716049 | 0.0000003790 |
| 8-1-1-1-1-0 | 356,400 | 0.0001637279 | 0.0007716049 | 0.0000001263 |
| 7-5-0-0-0-0 | 23,760 | 0.0000109152 | 0.0001286008 | 0.0000000014 |
| 7-4-1-0-0-0 | 475,200 | 0.0002183039 | 0.0001286008 | 0.0000000281 |
| 7-3-2-0-0-0 | 950,400 | 0.0004366077 | 0.0001286008 | 0.0000000561 |
| 7-3-1-1-0-0 | 2,851,200 | 0.0013098232 | 0.0001286008 | 0.0000001684 |
| 7-2-2-1-0-0 | 4,276,800 | 0.0019647348 | 0.0001286008 | 0.0000002527 |
| 7-2-1-1-1-0 | 5,702,400 | 0.0026196464 | 0.0001286008 | 0.0000003369 |
| 7-1-1-1-1-1 | 570,240 | 0.0002619646 | 0.0001286008 | 0.0000000337 |
| 6-6-0-0-0-0 | 13,860 | 0.0000063672 | 0.0000214335 | 0.0000000001 |
| 6-5-1-0-0-0 | 665,280 | 0.0003056254 | 0.0000214335 | 0.0000000066 |
| 6-4-2-0-0-0 | 1,663,200 | 0.0007640635 | 0.0000214335 | 0.0000000164 |
| 6-4-1-1-0-0 | 4,989,600 | 0.0022921906 | 0.0000214335 | 0.0000000491 |
| 6-3-3-0-0-0 | 1,108,800 | 0.0005093757 | 0.0000214335 | 0.0000000109 |
| 6-3-2-1-0-0 | 19,958,400 | 0.0091687624 | 0.0000214335 | 0.0000001965 |
| 6-3-1-1-1-0 | 13,305,600 | 0.0061125083 | 0.0000214335 | 0.0000001310 |
| 6-2-2-2-0-0 | 4,989,600 | 0.0022921906 | 0.0000214335 | 0.0000000491 |
| 6-2-2-1-1-0 | 29,937,600 | 0.0137531436 | 0.0000214335 | 0.0000002948 |
| 6-2-1-1-1-1 | 9,979,200 | 0.0045843812 | 0.0000214335 | 0.0000000983 |
| 5-5-2-0-0-0 | 997,920 | 0.0004584381 | 0.0000035722 | 0.0000000016 |
| 5-5-1-1-0-0 | 2,993,760 | 0.0013753144 | 0.0000035722 | 0.0000000049 |
| 5-4-3-0-0-0 | 3,326,400 | 0.0015281271 | 0.0000035722 | 0.0000000055 |
| 5-4-2-1-0-0 | 29,937,600 | 0.0137531436 | 0.0000035722 | 0.0000000491 |
| 5-4-1-1-1-0 | 19,958,400 | 0.0091687624 | 0.0000035722 | 0.0000000328 |
| 5-3-3-1-0-0 | 19,958,400 | 0.0091687624 | 0.0000035722 | 0.0000000328 |
| 5-3-2-2-0-0 | 29,937,600 | 0.0137531436 | 0.0000035722 | 0.0000000491 |
| 5-3-2-1-1-0 | 119,750,400 | 0.0550125743 | 0.0000035722 | 0.0000001965 |
| 5-3-1-1-1-1 | 19,958,400 | 0.0091687624 | 0.0000035722 | 0.0000000328 |
| 5-2-2-2-1- | 59,875,200 | 0.0275062872 | 0.0000035722 | 0.0000000983 |
| 5-2-2-1-1-1 | 59,875,200 | 0.0275062872 | 0.0000035722 | 0.0000000983 |
| 4-4-4-0-0-0 | 693,000 | 0.0003183598 | 0.0000005954 | 0.0000000002 |
| 4-4-3-1-0-0 | 24,948,000 | 0.0114609530 | 0.0000005954 | 0.0000000068 |
| 4-4-2-2-0-0 | 18,711,000 | 0.0085957147 | 0.0000005954 | 0.0000000051 |
| 4-4-2-1-1-0 | 74,844,000 | 0.0343828589 | 0.0000005954 | 0.0000000205 |
| 4-4-1-1-1-1 | 12,474,000 | 0.0057304765 | 0.0000005954 | 0.0000000034 |
| 4-3-3-2-0-0 | 49,896,000 | 0.0229219060 | 0.0000005954 | 0.0000000136 |
| 4-3-3-1-1-0 | 99,792,000 | 0.0458438119 | 0.0000005954 | 0.0000000273 |
| 4-3-2-2-1-0 | 299,376,000 | 0.1375314358 | 0.0000005954 | 0.0000000819 |
| 4-3-2-1-1-1 | 199,584,000 | 0.0916876238 | 0.0000005954 | 0.0000000546 |
| 4-2-2-2-2-0 | 37,422,000 | 0.0171914295 | 0.0000005954 | 0.0000000102 |
| 4-2-2-2-1-1 | 149,688,000 | 0.0687657179 | 0.0000005954 | 0.0000000409 |
| 3-3-3-3-0-0 | 5,544,000 | 0.0025468784 | 0.0000000992 | 0.0000000003 |
| 3-3-3-2-1-0 | 133,056,000 | 0.0611250826 | 0.0000000992 | 0.0000000061 |
| 3-3-3-1-1-1 | 44,352,000 | 0.0203750275 | 0.0000000992 | 0.0000000020 |
| 3-3-2-2-2-0 | 99,792,000 | 0.0458438119 | 0.0000000992 | 0.0000000045 |
| 3-3-2-2-1-1 | 299,376,000 | 0.1375314358 | 0.0000000992 | 0.0000000136 |
| 3-2-2-2-2-1 | 149,688,000 | 0.0687657179 | 0.0000000992 | 0.0000000068 |
| 2-2-2-2-2-2 | 7,484,400 | 0.0034382859 | 0.0000000165 | 0.0000000001 |
| 全部的 | 2,176,782,336 | 1.0000000000 | 0.0000037953 |
平均而言,需要擲多少次公平的骰子才能讓每個面至少擲兩次?
點擊下面的按鈕以取得答案。
這是我的解決方案。 (PDF)
我在Wizard of Vegas論壇上提出並討論了這個問題。
假設擲一個公平的六面骰子,直到出現1、2、3或6。如果1、2或3是這些遊戲結束數字中第一個出現的,那麼您什麼也贏不了。如果6是這些遊戲結束數字中第一個出現的,那麼您每次擲骰子都會贏得1美元。這場比賽的平均贏利是多少?
點擊下面的按鈕,查看幾個可能對您有幫助的無窮級數公式。
[劇透=提示]
提示 1:對 n 求 i = 0 到 ∞ 的和i = 1 / (1-n)
提示 2:i = 0 到 ∞ 的 i × n 總和i = n / (1-n) 2
[/spoiler]點擊下面的按鈕以取得答案。
點擊下面的按鈕以取得解決方案。
[劇透=解]
假設擲一個公平的六面骰子,直到出現1、2、3或6。如果1、2或3是這些遊戲結束數字中第一個出現的,那麼您什麼也贏不了。如果6是這些遊戲結束數字中第一個出現的,那麼您每次擲骰子都會贏得1美元。這場比賽的平均贏利是多少?
提示 1:對 n 求 i = 0 到 ∞ 的和i = 1 / (1-n)
提示 2:i = 0 到 ∞ 的 i × n 總和i = n / (1-n) 2
預期贏利可以表示為 i = 0 到 ∞ 的 (1 + i) * (1/3) i * (1/6) 總和。 =
(1/6)* (1/3) i 的 i = 0 到 ∞ 的總和+ (1/6)* (i * (1/3) i ) 的 i = 0 到 ∞ 的總和。
讓我們逐一評估一下。
i = 0 到 ∞ 的和,其中 (1/3) i =
1 / (1 - (1/3)) =
1 / (2/3) =
3/2
i = 0 到 ∞ 的和 (i * (1/3) i ) =
(1/3)/(1-(1/3)) 2 =
(1/3)/(4/9)=
(1/3)*(9/4)=
3/4
綜合起來,答案是
(1/6)*(3/2)+(1/6)*(3/4)=
(1/4)+(1/8)=
3/8
[/spoiler]我在Wizard of Vegas論壇上提出並討論了這個問題。
擲一個公平的骰子,每個面至少擲出兩次,預期擲骰子的次數是多少?
[劇透=解]
雖然這個問題可以用冗長乏味的馬可夫鏈來解決,但我更喜歡用積分法。我在我的Fire Bet和Bonus Craps頁面中解釋瞭如何使用這種方法。
想像一下,重大事件不再由一次擲骰子決定,而是被視為一個時間瞬間。假設事件之間的時間間隔具有無記憶性,平均間隔為一個時間單位。換句話說,事件之間的時間間隔服從平均值為1的指數分佈。這對裁決賭注來說無關緊要,因為事件仍然是一次一個地發生的。
根據泊松分佈,在 x 個單位時間內,骰子任一面擲出次數為零的機率為 exp(-x/6)*(x/6) 0 /0! = exp(-x/6)。泊松分佈也表示,任一面擲出恰好一次的機率為 exp(-x/6)*(x/6) 1 /1! = exp(-x/6) * (x/6)。因此,任一面在 x 個單位時間內擲出兩次或兩次以上機率為 1 - exp(-x/6)*(1 + (x/6))。六面擲出至少兩次的機率為 (1 - exp(-x/6)*(1 + (x/6))) 6。至少有一面未擲出至少兩次的機率等於:
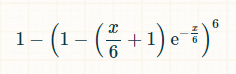
我們需要將其與所有時間結合起來,以找出平均需要多長時間才能實現預期目標。
幸運的是,我們此時可以使用積分計算器。對於連結中的那個,在「計算積分」後面的文字方塊中輸入 1- (1 - exp(-x/6)*(1 + x/6))^6 dx = apx. 24.1338692,並在自訂下將積分的邊界設為 0 到 ∞。
答案是 390968681 / 16200000 = 約 24.13386919753086
[/spoiler]我在Wizard of Vegas論壇上提出並討論了這個問題。
你先用一個公平的六面骰擲六次,記錄每次擲出的結果。然後,你把這些數字寫在另一個沒有標籤的公平骰子的六個面上。例如,如果你擲出的六次結果是3、5、3、6、1和2,那麼你的第二個骰子上就不會出現4,而是會出現兩個3。
接下來,你把第二顆骰子擲六次。把這六個數字寫在另一個公平骰子上,然後繼續這個過程,用前一個骰子產生一個新的骰子。
最終,你會得到一個六個面點數都相同的骰子。為了達到這個狀態,從一個骰子轉換到另一個骰子的平均次數是多少(或是總擲骰數除以6)?
[劇透=解]
為了避免混淆,我們用字母而不是數字來標記初始骰子。我們用字母標記每個可能的骰子狀態。例如,AAABBC 表示三個相同字母,兩個相同字母,一個相同字母。初始狀態顯然是 ABCDEF。
令 E(ABCDEF) 為從狀態 ABCDEF 開始的預期擲骰次數。
E(ABCDEF) = 1 + [180 × E(AAAAAB) + 450 × E(AAAABB) + 300 × E(AAABBB) + 1800 × E(AAAABC) + 7200 × E(AAABBC) + 1800 × E(AABBCC) + 7200 × E(AAABBC) + 1800 × E(AABB ×) + AAA ×BAA × E(AAABBC) + 1800 × E(AABB) + AAA ×BAA.202020000000000+) + 20202022229 × +202022) +2020202022) +20202,000 E(AABCDE) + 720 × E(ABCDEF)]/46656基於從一個狀態到另一個狀態的組合數量,下面的轉換矩陣顯示了從每個初始狀態(左列)到每個新狀態的轉換方式數量。順便說一下,這花了幾個小時才建造好。
過渡矩陣A
| 狀態 前 | 啊啊啊啊 | AAAAB | AAAABB | AAABBB | AAAABC | AAABBC | 美國商務部商務合作委員會 | AAAABCD | ABCD | ABCDE | ABCDEF |
|---|---|---|---|---|---|---|---|---|---|---|---|
| AAAAB | 15,626 | 18,780 | 9,750 | 2,500 | - | - | - | - | - | - | - |
| AAAABB | 4,160 | 13,056 | 19,200 | 10,240 | - | - | - | - | - | - | - |
| AAABBB | 1,458 | 8,748 | 21,870 | 14,580 | - | - | - | - | - | - | - |
| AAAABC | 4,098 | 12,348 | 8,190 | 2,580 | 7,920 | 10,080 | 1,440 | - | - | - | - |
| AAABBC | 794 | 5,172 | 8,670 | 5,020 | 6,480 | 17,280 | 3,240 | - | - | - | - |
| 美國商務部商務合作委員會 | 192 | 2,304 | 5,760 | 3,840 | 5,760 | 23,040 | 5,760 | - | - | - | - |
| AAAABCD | 732 | 4,464 | 4,140 | 1,680 | 7,920 | 14,400 | 2,520 | 4,320 | 6,480 | - | - |
| ABCD | 130 | 1,596 | 3,150 | 1,940 | 5,280 | 16,800 | 3,600 | 4,800 | 9,360 | - | - |
| ABCDE | 68 | 888 | 1,380 | 760 | 3,960 | 11,520 | 2,520 | 7,200 | 14,040 | 4,320 | - |
| ABCDEF | 6 | 180 | 450 | 300 | 1,800 | 7,200 | 1,800 | 7,200 | 16,200 | 10,800 | 720 |
我不會長篇大論地講解矩陣代數,只是假設矩陣 B 如下:
矩陣B
| 狀態 前 | AAAAB | AAAABB | AAABBB | AAAABC | AAABBC | 美國商務部商務合作委員會 | AAAABCD | ABCD | ABCDE | ABCDEF |
|---|---|---|---|---|---|---|---|---|---|---|
| AAAAB | -27876 | 9750 | 2500 | 0 | 0 | 0 | 0 | 0 | 0 | -46656 |
| AAAABB | 13056 | -27456 | 10240 | 0 | 0 | 0 | 0 | 0 | 0 | -46656 |
| AAABBB | 8748 | 21870 | -32076 | 0 | 0 | 0 | 0 | 0 | 0 | -46656 |
| AAAABC | 12348 | 8190 | 2580 | -38736 | 10080 | 1440 | 0 | 0 | 0 | -46656 |
| AAABBC | 5172 | 8670 | 5020 | 6480 | -29376 | 3240 | 0 | 0 | 0 | -46656 |
| 美國商務部商務合作委員會 | 2304 | 5760 | 3840 | 5760 | 23040 | -40896 | 0 | 0 | 0 | -46656 |
| AAAABCD | 4464 | 4140 | 1680 | 7920 | 14400 | 2520 | -42336 | 6480 | 0 | -46656 |
| ABCD | 1596 | 3150 | 1940 | 5280 | 16800 | 3600 | 4800 | -37296 | 0 | -46656 |
| ABCDE | 888 | 1380 | 760 | 3960 | 11520 | 2520 | 7200 | 14040 | -42336 | -46656 |
| ABCDEF | 180 | 450 | 300 | 1800 | 7200 | 1800 | 7200 | 16200 | 10800 | -46656 |
答案是矩陣 B 的行列式與矩陣 A 的行列式之比:
確定(A)= 1,461,067,501,120,670,000,000,000,000,000,000,000,000,000,000,000
確定(B)= 14,108,055,348,203,100,000,000,000,000,000,000,000,000,000,000,000
Determ(B) / Determ(A) = 約 9.65599148388557
[/spoiler]如果您擲一個骰子 20 次,那麼至少一次擊中所有六面的機率是多少?
[劇透=解]
答案可以近似表示為 1 - (prob(沒有 1) + prob(沒有 2) + ... + prob(沒有 6)) = 1 - 6*(5/6)^20 = apx. 0.84349568。
然而,這會導致雙倍減去兩種不同面從未擲過的情況。從六種面中選擇兩種面,一共有(6,2)=15種方法。任兩種給定面從未擲過的機率是(4/6)^20。我們需要將這些值加到機率中,因為它們在上一個步驟中被減去了兩次。所以,現在我們得到的結果是 1 - 6*(5/6)^20 + 15*(4/6)^20 = 約 0.84800661。
我在Wizard of Vegas論壇上提出並討論了這個問題。
然而,如果任何一組從未擲出的三面在第一步中被三次減去,在第二步中被三次加去,我們需要將它們減去,因為六面中並非所有面都擲出了。從六面中選擇三面共有 combin(6,3) = 20 種方法。任何特定的三面從未擲出的機率是 (3/6)^20。所以,現在我們得到的結果是 1 - 6*(5/6)^20 + 15*(4/6)^20 - 20*(3/6)^20= 約 0.847987537。
然而,如果任何一組從未擲出的四面在第一步中被減去四倍,在第二步中被加去四倍,在第三步中被減去四倍,我們需要將它們加回去,因為每個這樣的狀態已經被減去了兩次。從六面中選擇四面,共有 combin(6,4) = 15 種方法。任何特定的四面從未擲出的機率是 (2/6)^20。所以,現在我們得到的結果是 1 - 6*(5/6)^20 + 15*(4/6)^20 - 20*(3/6)^20 + 15*(2/6)^20 = 約 0.84798754089。
然而,如果20次擲出的點數都相同,那麼第一步就應該減去五倍,再加去五倍,第三步再減去五倍,第四步再加去五倍。我們需要把這些點數減掉。所以,現在我們得到的結果是:1 - 6*(5/6)^20 + 15*(4/6)^20 - 20*(3/6)^20 + 15*(2/6)^20 - 6*(1/6)^20 = 約 0.84798754089。
所以答案是 1-6*(5/6)^20+COMBIN(6,4)*(4/6)^20-COMBIN(6,3)*(3/6)^20+COMBIN(6,2)*(2/6)^20-6*(1/6)^20 = 約 0.847987898989。 [/劇透]
你有兩顆骰子。你可以隨意給兩顆骰子的每一面編號,只要每一面都是大於或等於1的整數即可。你可以在同一個骰子上重複相同的數字,並且可以隨意增加點數。除了製作標準骰子外,如何給它們編號,使任何給定點數的機率都與標準骰子相同?
骰子 1 = 1,2,2,3,3,4。
骰子 2 = 1,3,4,5,6,8。
恐怕我對這個問題的解決方案基本上是反覆試驗。
使用兩個骰子,要獲得 2 到 12 的總數,平均需要擲多少次?
投擲死亡遊戲 (Drop Dead) 使用五個標準骰子進行。回合開始時,您需擲出所有五顆骰子。如果所有骰子都不是 2 或 5,則計算所有骰子點數總和,並將結果加到您的點數中,然後重新擲骰。如果擲出任何 2 或 5,則您的本輪得分為零。所有顯示 2 或 5 的骰子均視為死點,並作廢。然後,您使用剩餘的骰子重新擲骰。遊戲繼續,您可以選擇得分或移除骰子。當所有骰子都被移除後,您的回合結束,即您被判定為投擲死亡。所有得分將加在一起,作為您的最終得分。得分高者獲勝。
您對這場比賽的預期得分是多少?
[劇透=解]
讓我們從剩下一個骰子的場景開始並向後移動。
設變數 a 為剩餘一個骰子時的預期附加點數。
除 2 或 5 之外的平均擲點數為 (1+3+4+6)/4 = 7/2。
a = (2/3)×(a + 7/2)。
a/3 = 7/3。
a = 7。
接下來我們計算一下剩下兩顆骰子的預期點數b。
b = (2/3) 2 ×(b + 2 × (7/2)) + 2×(2/3)×(1/3)×a。
b = 11.2。
接下來我們計算一下剩下三個骰子的預期點數c。
c = (2/3) 3 ×(c + 3× (7/2)) + 3×(2/3) 2 ×(1/3)×b + 3×(2/3)×(1/3) 2 ×b。
c = 1302/95 = 13.705263。
接下來,我們來計算剩下四顆骰子的預期點數d。
d = (2/3) 4 ×(d + 4× (7/2)) + 4×(2/3) 3 ×(1/3)×c + 6×(2/3) 2 ×(1/3) 2 ×b + 4×(2/3)×(1/3) 3 ×a。
d = 3752/247 = 15.190283。
最後,我們來計算一下剩下五顆骰子的預期點數e。
e = (2/3) 5 ×(e + 5×(7/2)) + 5×(2/3) 4 ×(1/3)×d + 10×(2/3) 3 ×(1/3) 2 ×c + 10×(2/3) 2 ×(1/3) 3 ×b + ×(23/3 ) 。
e = 16.064662。
我在Wizard of Vegas論壇上提出並討論了這個問題。
重複擲兩顆骰子,一個紅色骰子,一個藍色骰子。記錄每個骰子的點數總和。當兩顆骰子點數相等時,預期角色數是多少?
[劇透=更多評論]
很難解釋為什麼答案是無限大。更令人困惑和矛盾的是,總數相等的機率是1。
下表顯示了 1 至 16 次投擲後總數首次相同的機率。
機率首次等於總數
| 麵包捲 | 可能性 |
|---|---|
| 1 | 0.166667 |
| 2 | 0.112654 |
| 3 | 0.092850 |
| 4 | 0.080944 |
| 5 | 0.072693 |
| 6 | 0.066539 |
| 7 | 0.061722 |
| 8 | 0.057819 |
| 9 | 0.054573 |
| 10 | 0.051819 |
| 11 | 0.049443 |
| 12 | 0.047367 |
| 十三 | 0.045532 |
| 14 | 0.043895 |
| 15 | 0.042423 |
| 16 | 0.041089 |
Excel 顯示與該曲線非常接近的擬合值為 y = 0.1784*x-1.011,其中 x = 滾動次數,y = 機率。
這個無窮級數的和是無限大。
[/spoiler]我在Wizard of Vegas論壇上提出並討論了這個問題。
擲出五個紅色骰子和五個藍色骰子。無論擲骰子的順序為何,擲出相同點數的機率是多少?例如,擲出的點數都是 1-2-3-3-6。
下表顯示了任何類型的捲:
- 擲出此牌型的不同組合數。例如,對於葫蘆,三條有六種組合,對子有五種組合,總共有30種不同的葫蘆組合。
- 順序數。例如,對於葫蘆,有 combin(5,3)=10 種方法可以從五個骰子中選擇三個組成三個。另外兩顆骰子必須是對子。
- 給定牌型的擲出方式數量。這是前兩列的乘積。例如,葫蘆有 30 * 10 = 300 種擲出方式。
- 手牌的機率。例如,葫蘆的機率為 300/6 5 = 0.038580。
- 兩次擲出相同點數且屬於給定牌型的機率。這是第四列機率的平方除以第二列。例如,兩次擲出相同點數的機率為 0.038580 2 。然而,兩次擲出相同點數的機率為 1/30。因此,兩次擲出相同點數的機率為 0.038580 2 /30 = 0.00004961。
右下角單元格顯示兩次擲骰結果相同的總機率為 0.00635324。
匹配卷
| 類型 卷 | 不同的 類型 | 訂單 | 全部的 組合 | 可能性 一卷 | 可能性 兩卷 | |
|---|---|---|---|---|---|---|
| 五張相同的牌 | 6 | 1 | 6 | 0.00077160 | 0.00000010 | |
| 四條 | 三十 | 5 | 150 | 0.01929012 | 0.00001240 | |
| 客滿 | 三十 | 10 | 300 | 0.03858025 | 0.00004961 | |
| 三條 | 60 | 20 | 1,200 | 0.15432099 | 0.00039692 | |
| 兩對 | 60 | 三十 | 1,800 | 0.23148148 | 0.00089306 | |
| 一對 | 60 | 60 | 3,600 | 0.46296296 | 0.00357225 | |
| 五個單身人士 | 6 | 120 | 720 | 0.09259259 | 0.00142890 | |
| 全部的 | 7,776 | 1.00000000 | 0.00635324 |
擲一個六面骰子,直到發生以下任一事件:
A) 任何一方都出現了六次。
B) 每一方都至少出現過一次。
事件 A 先發生的機率是多少?
為了像我一樣使用微積分來回答這個問題,我建議使用積分計算器,例如integral-calculator.com/上的那個。
這是我的解決方案(PDF)。
這個問題在我的Wizard of Vegas論壇中被提出(用略有不同的措辭)並被討論過。
你想玩一個需要普通六面骰的遊戲。很遺憾,你把骰子弄丟了。不過,你有四張索引卡,你可以隨意標記。玩家必須從這四張卡中隨機選擇兩張,不能重複,然後計算兩張卡的點數總和。
如何給卡片編號,使得兩張不同卡片的總和代表擲骰子的次數?
給它們編號為 0、1、2 和 4。
從四張牌中抽出兩張的方法有以下六種。
- 0+1=1
- 0+2=2
- 1+2=3
- 0+4=4
- 1+4=5
- 2+4=6
我在Wizard of Vegas論壇上提出並討論了這個問題。
一枚六面骰子重複擲出,直到總點數達到或超過13。最終點數的平均值、中位數和眾數是多少?
中位數 = 14
模式 = 13
[劇透=解]
我不得不用馬可夫鏈來解決這個問題。下表根據左列的累積和顯示了每個最終總數的機率。首先從 13 到 18 的明顯情況開始。然後,對於 0 到 12 的累積和,取下面六個單元格的平均值。
可以在第一行找到初始狀態的機率,其總和為 0。
馬可夫鏈
| 擲骰子總數 | 十三 | 14 | 15 | 16 | 17 | 18 |
|---|---|---|---|---|---|---|
| 0 | 0.279263 | 0.236996 | 0.192313 | 0.145585 | 0.097371 | 0.048472 |
| 1 | 0.290830 | 0.230791 | 0.188524 | 0.143842 | 0.097114 | 0.048899 |
| 2 | 0.293393 | 0.241931 | 0.181893 | 0.139625 | 0.094943 | 0.048215 |
| 3 | 0.289288 | 0.245178 | 0.193717 | 0.133678 | 0.091410 | 0.046728 |
| 4 | 0.280369 | 0.242560 | 0.198450 | 0.146988 | 0.086950 | 0.044682 |
| 5 | 0.268094 | 0.235687 | 0.197878 | 0.153768 | 0.102306 | 0.042267 |
| 6 | 0.253604 | 0.225827 | 0.193419 | 0.155611 | 0.111500 | 0.060039 |
| 7 | 0.360232 | 0.193566 | 0.165788 | 0.133380 | 0.095572 | 0.051462 |
| 8 | 0.308771 | 0.308771 | 0.142104 | 0.114326 | 0.081919 | 0.044110 |
| 9 | 0.264660 | 0.264660 | 0.264660 | 0.097994 | 0.070216 | 0.037809 |
| 10 | 0.226852 | 0.226852 | 0.226852 | 0.226852 | 0.060185 | 0.032407 |
| 11 | 0.194444 | 0.194444 | 0.194444 | 0.194444 | 0.194444 | 0.027778 |
| 12 | 0.166667 | 0.166667 | 0.166667 | 0.166667 | 0.166667 | 0.166667 |
| 十三 | 1.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 |
| 14 | 0.000000 | 1.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 |
| 15 | 0.000000 | 0.000000 | 1.000000 | 0.000000 | 0.000000 | 0.000000 |
| 16 | 0.000000 | 0.000000 | 0.000000 | 1.000000 | 0.000000 | 0.000000 |
| 17 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 1.000000 | 0.000000 |
| 18 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 1.000000 |
這個問題是在我的論壇“ 拉斯維加斯巫師”中提出並討論的。
如您所知,如果在擲出 7 之前擲出從 2 到 12 的所有數字(除 7 之外),則擲骰子遊戲中的「全部下注」獲勝。如果獲勝,平均需要擲多少次才能贏得這個賭注?
我看到有人聲稱在擲骰子遊戲桌上連續目擊了18個(總共11個)的「young」(young)。平均需要擲幾次才能觀察到這種情況?
這是我的解決方案(PDF)。
一對公平的六面骰子被反覆擲出,直到發生以下兩個事件之一:
A) 總共擲出 12 點。
B) 連續兩次擲出總數為 7。
哪一個更有可能先發生?
> [劇透=解]
讓:
- p = 從初始狀態開始先擲出 12 的機率,或是當前一次擲出的點數不是 7 時。
- q = 上次擲出的點數為 7 時,先擲出 12 的機率。
這就是所謂的馬可夫鏈問題。
在我們討論這一點之前,回想一下擲出總數 7 的機率是 1/6,擲出總數 12 的機率是 1/36。
我們可以根據 p 和 q 相互定義,如下所示:
- (1)p =(1/36)+(6/36)q +(29/36)p
- (2)q = (1/36) + (29/36)p
我們將公式 (1) 乘以 36:
36便士=1+6q+29便士
(3)7p = 1 + 6q
我們將 (2) 式中的 q 值代入 (3) 式中:
7p = 1 + 6*((1/36) + (29/36)p)
7便士=1+(1/6)+(29/6)便士
42便士=6+1+29便士
13便士=7
q = 7/13
因此,先擲出 12 的機率是 7/13 =~ 53.85%。
因此,首先擲出兩個連續 7 的機率為 46.15%。
因此,更有可能的是先擲出總數 12。



