非賭場遊戲 - 常問問題
我喜歡用美元玩「說謊者撲克」遊戲。請問一張鈔票上出現任一個相同數字的機率是多少?謝謝。如果我和三個人一起玩,任何一個數字出現的機率是多少?
首先,讓我來回答一個未被提及的問題:某個特定數字在一張隨機鈔票上出現 n 次的機率。一張鈔票上有 8 位數字,因此特定數字出現 n 次的機率為 combin(8,n)*0.1 n *0.9 8-n /10 8 。下表顯示了特定數字出現 0 到 8 次的機率。
騙子撲克中的特定數字賠率
| 數位 | 可能性 |
|---|---|
| 8 | 0.00000001 |
| 7 | 0.00000072 |
| 6 | 0.00002268 |
| 5 | 0.00040824 |
| 4 | 0.00459270 |
| 3 | 0.03306744 |
| 2 | 0.14880348 |
| 1 | 0.38263752 |
| 0 | 0.43046721 |
| 全部的 | 1.00000000 |
下表列出了每種可能出現的鈔票類型的機率,按每種類型的數量分類。例如,序號 66847680 的鈔票可能出現一張三張同點鈔票、一張對子鈔票和三張單張鈔票,機率為 0.1693440。
說謊者撲克中的一般機率
| 8 橡木 | 7 橡木 | 6 橡木 | 5 橡木 | 4 橡木 | 3 橡木 | 2 橡木 | 1 橡木 | 可能性 |
|---|---|---|---|---|---|---|---|---|
| 1 | 0.0000001 | |||||||
| 1 | 1 | 0.0000072 | ||||||
| 1 | 1 | 0.0000252 | ||||||
| 1 | 2 | 0.0002016 | ||||||
| 1 | 1 | 0.0000504 | ||||||
| 1 | 1 | 1 | 0.0012096 | |||||
| 1 | 3 | 0.0028224 | ||||||
| 2 | 0.0000315 | |||||||
| 1 | 1 | 1 | 0.0020160 | |||||
| 1 | 2 | 0.0015120 | ||||||
| 1 | 1 | 2 | 0.0211680 | |||||
| 1 | 4 | 0.0211680 | ||||||
| 2 | 1 | 0.0020160 | ||||||
| 2 | 2 | 0.0141120 | ||||||
| 1 | 2 | 1 | 0.0423360 | |||||
| 1 | 1 | 3 | 0.1693440 | |||||
| 1 | 5 | 0.0846720 | ||||||
| 4 | 0.0052920 | |||||||
| 3 | 2 | 0.1270080 | ||||||
| 2 | 4 | 0.3175200 | ||||||
| 1 | 6 | 0.1693440 | ||||||
| 8 | 0.0181440 | |||||||
| 全部的 | 1.0000000 | |||||||
橡木 = “一種”
欲了解更多信息,請參閱我的“騙子撲克”頁面。
美國銀行正提供一項活動,每天選定一筆透過ATM進行的存款,將其金額變為三倍。此活動持續約兩個月。若我想提高中獎機率,是存入300美元...還是分三次存入100美元更好...又或者整體中獎機率實在太低,根本不值得費心去比較這些差異?
無論您將總存款分成多少次進行,預期的贏利都是相同的。一個不錯的策略是盡可能多次地重複存取同一筆資金。然而,您的勝算可能太低,以至於不值得這麼麻煩。
想問一下關於東方骰子遊戲的問題。遊戲中玩家需要猜測骰子的哪一面朝上。玩家先在1、2、3、4、5、6上投注(類似輪盤賭),然後「莊家」會同時擲3個骰子。如果所選數字出現一次(在3個骰子中的任何一個上),賠率為1:1;如果所選數字出現兩次,則賠率為2:1;如果所選數字同時出現在3個骰子上,則賠率為3:1。由於玩家可以任意下注,那麼最佳下注數是多少? (假設我所有賭注的金額相同)
在 Windows 版本中贏得標準 Klondike Solitaire 遊戲的幾率是多少?
這大概是我最常被問到卻又無法回答的問題了。至今為止,還沒有人做過完整的克朗代克紙牌遊戲。或許,等電腦速度提升一百萬倍,最終會有人做到。不過,據說拉斯維加斯的賭場至少在五十年代就提供過這種遊戲。我問過不少拉斯維加斯老玩家,想證實這一點,但至今無人能證實。
我最近在玩西洋雙陸棋時,連續四次擲出雙六。這種情況再次發生的機率是多少?
每次新擲骰子時,接下來四次擲骰子均為雙六的機率為 (1/36) 4 = 1/1679616。
您好, www.transience.com.au/ pearl.html 上有一個叫做「豬玀珍珠」的遊戲。珍珠被分成三行(5+4+3),輪到你時,你可以從一行中移除任意數量的珍珠。遊戲的目標是把最後一顆珍珠留給對手。玩家(我)總是先手(也總是輸)。為什麼我總贏不了?我的對手有一個狡猾的策略,總是能贏,你能揭穿他的秘密嗎?
首先從3顆珍珠的那一行移除2顆珍珠,剩下1+4+5。無論對手在下一輪做什麼,都留下以下任一:1+1+1、1+2+3或4+4。用其中任一迫使對手陷入兩堆各有2顆或更多珍珠的局面,或奇數堆各有1顆珍珠的局面。
大富翁遊戲中的哪一套最好?
我最喜歡橘色組合。它能提供最佳的投資報酬率。例如,橘色組合中一家飯店的價格為500美元,平均租金為966.67美元,租金與費用比率為1.93。唯一一個比率較高的組合是淺藍色組合,為2.27。然而,淺藍色組合的最高租金只有600美元。橘色組合中三棟房屋的租金與淺藍色組合中的飯店相同,但成本低20%,而且還有擴建空間。此外,橙色組合非常適合剛出獄的人。所以聽我的建議,交易時盡量買橘色組合。
您對玩石頭/剪刀/布有什麼建議?
本站最好的建議可能是:第一輪,總是選布。這是因為業餘玩家往往第一次就選石頭。只要每次伸出手,一次一個,你就會發現石頭是最舒服、最自然的選擇。如果你重複玩幾輪,你應該選擇任何能在最後一輪擊敗對手的機率小於三分之一的牌。這是因為我相信業餘玩家重複玩的次數不到三分之一。如果你與一個你擔心會闖入你腦海的職業選手比賽,那麼通過查看手錶的秒針隨機化,將秒數除以三取餘數,然後將餘數映射如下:0=石頭,1=剪刀,2=布(或任何其他提前確定的映射)。所以下次你去荷蘭式餐廳時,我建議你先玩一輪結帳,然後再選布。你以後會感謝我的。
當攻擊者擲出三個骰子而防禦者擲出兩顆骰子時,誰在風險中佔有優勢?
對於不熟悉這款遊戲的人來說,《Risk》是有史以來最偉大的桌遊。沒玩過的人還不算真正體驗過。在常見的3對2戰鬥中,以下是可能的結果:
- 防守方兩敗俱傷:37.17%
- 各輸一分:33.58%
- 攻擊者兩敗俱傷:29.26%
在 Yahtzee 遊戲中,如果卡片上只剩下 Yahtzee 本身,那麼成功的可能性是多少?
下表根據您玩 Yahtzee 所需的額外骰子數量顯示了最後一次擲骰子的成功機率。
最後擲骰子機率
| 需要 | 可能性 成功 |
| 0 | 1 |
| 1 | 0.166667 |
| 2 | 0.027778 |
| 3 | 0.00463 |
| 4 | 0.000772 |
下表顯示了改進的機率。左列顯示每次擲骰前需要擲出幾個骰子,上列顯示每次擲骰後需要擲出多少個骰子。正文部分顯示了達到給定改進程度的機率。
改進的可能性
| 滾動前需要 | 0 | 1 | 2 | 3 | 4 | 全部的 |
| 0 | 1 | 0 | 0 | 0 | 0 | 1 |
| 1 | 0.166667 | 0.833333 | 0 | 0 | 0 | 1 |
| 2 | 0.027778 | 0.277778 | 0.694444 | 0 | 0 | 1 |
| 3 | 0.00463 | 0.069444 | 0.37037 | 0.555556 | 0 | 1 |
| 4 | 0.000772 | 0.01929 | 0.192901 | 0.694444 | 0.092593 | 1 |
下表顯示了首次擲骰子時需要 0 到 4 個骰子才能擲出 Yahtzee 的機率。
首次擲骰子機率
| 需要 | 可能性 |
| 0 | 0.000772 |
| 1 | 0.019290 |
| 2 | 0.192901 |
| 3 | 0.694444 |
| 4 | 0.092593 |
下表顯示了根據第一次擲骰子後所需擲骰子數,改進並最終成功的機率。例如,如果玩家需要再擲3個骰子才能完成Yahtzee遊戲,那麼第二次擲骰子後改進為再擲2個骰子並在第三次擲骰子時完成Yahtzee遊戲的機率為0.010288066。
根據第二次擲骰子前後所需的數字,第一次擲骰子後 Yahtzee 的機率
| 滾動前需要 | 0 | 1 | 2 | 3 | 4 | 全部的 |
| 0 | 1 | 0 | 0 | 0 | 0 | 1 |
| 1 | 0.166667 | 0.138889 | 0 | 0 | 0 | 0.305556 |
| 2 | 0.027778 | 0.046296 | 0.01929 | 0 | 0 | 0.093364 |
| 3 | 0.00463 | 0.011574 | 0.010288 | 0.002572 | 0 | 0.029064 |
| 4 | 0.000772 | 0.003215 | 0.005358 | 0.003215 | 0.000071 | 0.012631 |
要得到最終答案,請將前兩張牌上擲出所需的數字與最後一列上擲出一張牌的最終成功機率相乘。結果為:0.092593*0.012631+0.694444*0.029064+0.192901*0.093364+0.019290*0.305556+0.000772*1=4.6028643%。為了驗證這一點,我進行了1億次遊戲模擬,模擬的機率為4.60562%。
如果在石頭/剪刀/布遊戲中引入炸藥作為選項,其中炸藥擊敗石頭和布,但剪刀擊敗炸藥,那麼如果兩個完美的邏輯學家在玩,最佳策略應該是什麼?
首先,我們可以排除出紙的可能性。無論對方出什麼,你都可以用炸藥蓋住紙張來獲得相同或更好的結果。一旦紙被蓋住,炸藥就變成了新的紙,打敗了石頭,輸給了剪刀。所以,完美的策略是在石頭、剪刀和炸藥之間隨機選擇,而且機率相同。
當你必須在有限的時間內收集盡可能多的錢時,在那些四處飄散的錢攤位中,最好的策略是什麼?
我向Fun Industries Inc.的Randy Hill諮詢了這個問題。他說你應該伸直手臂,手掌向下,讓錢在你的手掌和手臂底部膨脹起來。等到錢存夠了,就把錢塞進投幣口。
假設我們有一個賭博遊戲。一枚無偏硬幣被重複拋擲。每次拋擲,我們需要支付 1 盧比。結果有兩種可能:H 或 T。如果拋出正面和反面的差值為 3,我們將從賭徒那裡得到 8 盧比。我們應該玩這個遊戲嗎?為什麼?我們獲勝的機率是多少?當我們擲出 7 或 9 盧比時,什麼因素會影響獲勝機率?
我們將 x 稱為從起點開始的翻轉預期次數。
如果其中一方的翻轉次數佔多數,則我們將 y 稱為剩餘翻轉的預期次數。
如果一方的翻轉次數佔多數,則我們將 z 稱為剩餘翻轉的預期次數。
E(x) = 1 + E(y)
E(y) = 1 + 0.5*E(x) + 0.5*E(z)
E(z) = 1 + 0.5*E(y)
由此,用矩陣代數很容易得出 E(x) = 9,E(y) = 8,E(z) = 5。因此,平均需要拋擲 9 次才能使正面和反面的機率差達到 3。因此,對於每次拋擲都能贏取 1 盧比的人來說,8 盧比的賭注是一個不錯的選擇,因為他平均能贏取 9 盧比,但只損失 8 盧比。對賭徒來說,賭場優勢是 11.11%。 9 盧比的賭注是公平的,7 盧比的賭注則為 22.22%。
您在2002年11月28日的專欄中討論了《Pearls Before Swine》這款遊戲的正確策略。這款遊戲還有續作《Pearls Before Swine II》 。我該如何通關這個版本呢?
我在2002年11月28日那一欄解釋了只剩下三行時該如何玩。以下是我的四行策略。輪到你時,查看左欄的排列,然後根據右欄的排列進行遊戲。例如,起始位置3456列在最後,表示你應該從有5顆珍珠的那一行中移除4顆,剩下1346顆。如果左欄顯示“輸”,即使對手採取最優策略,你也絕對不可能獲勝,而Transcience的遊戲似乎總是如此。
這張表的一個規律似乎是,你應該迫使對手陷入這樣一種境地:最小行和最大行的珍珠總數等於中間兩行的珍珠總數。這意味著在珍珠數量最少的那一行留零。
明珠暗投 II 策略
| 你有 | 離開 |
| 1111 | 111 |
| 1112 | 111 |
| 1113 | 111 |
| 1114 | 111 |
| 1115 | 111 |
| 1116 | 111 |
| 1122 | 失去 |
| 1123 | 1122 |
| 1124 | 1122 |
| 1125 | 1122 |
| 1126 | 1122 |
| 1133 | 失去 |
| 1134 | 1133 |
| 1135 | 1133 |
| 1136 | 1133 |
| 1144 | 失去 |
| 1145 | 1144 |
| 1146 | 1144 |
| 1155 | 失去 |
| 1156 | 1155 |
| 1222 | 1122 |
| 1223 | 1122 |
| 1224 | 1122 |
| 1225 | 1122 |
| 1226 | 1122 |
| 1233 | 123 |
| 1234 | 123 |
| 1235 | 123 |
| 1236 | 123 |
| 1244 | 1144 |
| 1245 | 145 |
| 1246 | 246 |
| 1255 | 1155 |
| 1256 | 失去 |
| 1333 | 1133 |
| 1334 | 1133 |
| 1335 | 1133 |
| 1336 | 1133 |
| 1344 | 1144 |
| 1345 | 145 |
| 1346 | 失去 |
| 1355 | 1155 |
| 1356 | 1256 |
| 1444 | 1144 |
| 1445 | 1144 |
| 1446 | 1144 |
| 1455 | 1155 |
| 1456 | 1346 |
| 2222 | 失去 |
| 2223 | 2222 |
| 2224 | 2222 |
| 2225 | 2222 |
| 2226 | 2222 |
| 2233 | 失去 |
| 2234 | 2233 |
| 2235 | 2233 |
| 2236 | 2233 |
| 2244 | 失去 |
| 2245 | 2244 |
| 2246 | 2244 |
| 2255 | 失去 |
| 2256 | 2255 |
| 2333 | 2233 |
| 2334 | 2233 |
| 2335 | 2233 |
| 2336 | 2233 |
| 2344 | 2244 |
| 2345 | 失去 |
| 2346 | 1346 |
| 2355 | 2255 |
| 2356 | 2345 |
| 2444 | 2244 |
| 2445 | 2244 |
| 2446 | 2244 |
| 2455 | 2255 |
| 2456 | 2345 |
| 3333 | 失去 |
| 3334 | 3333 |
| 3335 | 3333 |
| 3335 | 3333 |
| 3336 | 3333 |
| 3344 | 失去 |
| 3345 | 3344 |
| 3346 | 3344 |
| 3355 | 失去 |
| 3356 | 3355 |
| 3444 | 3344 |
| 3445 | 3344 |
| 3446 | 3344 |
| 3455 | 3355 |
| 3456 | 1346 |
Brad S. 寫信來信,希望能增加一個適用於任意數量珍珠和行數的通用策略。首先,你需要將每一行分解成二進位部分。例如,Transscience 遊戲的起始位置如下。
- 3 = 2 + 1
- 4 = 4
- 5 = 4 + 1
- 6 = 4 + 2
然後,你盡量讓每個2的冪都留下偶數個。例如,上式中有兩個1、兩個2和三個4。所以多了一個4。然後,你從任何包含4的行中移除4。繼續這樣做,直到你能讓對手的1的數量減少到2、2或奇數個。
在《珍珠3》遊戲中試試這個策略,你每次都能贏。如果你像我在第10局遊戲(4+7+8+11)一開始就輸了,你可以點擊「走」讓他先走。
別再糾結你的NIM遊戲了!我一直以為獲勝的關鍵在於讓你的對手(這裡指的是電腦)留下的點數加起來等於下一個最小數字,這個數字等於它的二進位總和。也就是說,如果我有17個點,我取2個,剩下15個,也就是二進位數1、2、4、8的總和。但這似乎行不通。我是對還是錯?
你在二進制數上的思路沒錯,但這並非真正的致勝策略。首先,如果你能讓對手留下奇數行,每行一個,那就這樣做。否則,將每一行分解成二進位元素。例如,99 就是 64+32+2+1。然後把所有行上每個元素的數量加起來。最後,尋找一種能讓對手所有行上所有二進位元素數量為偶數的玩法。
我們來看一個例子。假設輪到你了,場景如下。
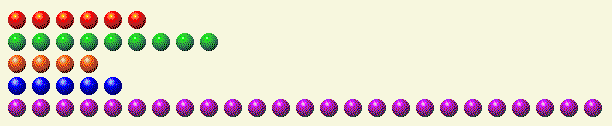
下表將每一行分解為二進位組件。
玩家第 1 回合
| 排 | 1 | 2 | 4 | 8 | 16 |
| 6 | 0 | 1 | 1 | 0 | 0 |
| 9 | 1 | 0 | 0 | 1 | 0 |
| 4 | 0 | 0 | 1 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 |
| 二十五 | 1 | 0 | 0 | 1 | 1 |
| 全部的 | 3 | 1 | 3 | 2 | 1 |
可以看到,1、2、4 和 16 的數量都是奇數。顯然,我們需要讓 25 這一行小於 16,才能消除 16 這個數字。為了讓二進位數字的和保持偶數,我們需要去掉 1,加上 2,加上 4,保留 8,然後去掉 16。這意味著最佳玩法是最後一行 2+4+8=14。保留最後一行 14,我們得到以下結果。
計算機的第一回合
| 排 | 1 | 2 | 4 | 8 | 16 |
| 6 | 0 | 1 | 1 | 0 | 0 |
| 9 | 1 | 0 | 0 | 1 | 0 |
| 4 | 0 | 0 | 1 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 |
| 14 | 0 | 1 | 1 | 1 | 0 |
| 全部的 | 2 | 2 | 4 | 2 | 0 |
計算機輪流做事,把這個留給我們。
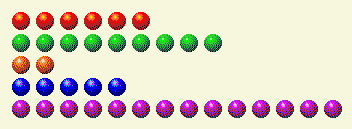
這是它的二進制分解。
玩家第 2 回合
| 排 | 1 | 2 | 4 | 8 | 16 |
| 6 | 0 | 1 | 1 | 0 | 0 |
| 9 | 1 | 0 | 0 | 1 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 |
| 14 | 0 | 1 | 1 | 1 | 0 |
| 全部的 | 2 | 3 | 3 | 2 | 0 |
這裡我們需要去掉一個 2 和一個 4,才能讓總數相等。只有一行,也就是 14,包含這兩個部分。所以從中去掉 6,剩下 8。
計算機的第二回合
| 排 | 1 | 2 | 4 | 8 | 16 |
| 6 | 0 | 1 | 1 | 0 | 0 |
| 9 | 1 | 0 | 0 | 1 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 |
| 8 | 0 | 0 | 0 | 1 | 0 |
| 全部的 | 2 | 2 | 2 | 2 | 0 |
計算機輪流做事,把這個留給我們。
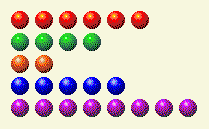
現在我們需要更改 1、4 和 8 列。
玩家第 3 回合
| 排 | 1 | 2 | 4 | 8 | 16 |
| 6 | 0 | 1 | 1 | 0 | 0 |
| 4 | 0 | 0 | 1 | 0 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 |
| 8 | 0 | 0 | 0 | 1 | 0 |
| 全部的 | 1 | 2 | 3 | 1 | 0 |
可以透過將行 8 更改為 5 來實現,如下所示。
計算機第 3 輪
| 排 | 1 | 2 | 4 | 8 | 16 |
| 6 | 0 | 1 | 1 | 0 | 0 |
| 4 | 0 | 0 | 1 | 0 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 |
| 全部的 | 2 | 2 | 4 | 0 | 0 |
計算機輪流做事,把這個留給我們。
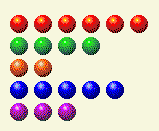
現在我們需要更改 2 和 4 的總數。
玩家回合 4
| 排 | 1 | 2 | 4 | 8 | 16 |
| 6 | 0 | 1 | 1 | 0 | 0 |
| 4 | 0 | 0 | 1 | 0 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 |
| 3 | 1 | 1 | 0 | 0 | 0 |
| 全部的 | 2 | 3 | 3 | 0 | 0 |
這可以透過將 6 更改為 0 來實現。
計算機第 4 回合
| 排 | 1 | 2 | 4 | 8 | 16 |
| 0 | 0 | 0 | 0 | 0 | 0 |
| 4 | 0 | 0 | 1 | 0 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 |
| 3 | 1 | 1 | 0 | 0 | 0 |
| 全部的 | 2 | 2 | 2 | 0 | 0 |
計算機輪流做事,把這個留給我們。
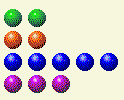
現在我們需要改變 2 和 4。
玩家第 5 回合
| 排 | 1 | 2 | 4 | 8 | 16 |
| 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 |
| 3 | 1 | 1 | 0 | 0 | 0 |
| 全部的 | 2 | 3 | 1 | 0 | 0 |
這可以透過將 5 行改為 3 行來實現。如果您能讓對手陷入 x,x,y,y 局面,您就必然會獲勝,前提是您可以將相同的局面保持到最後。
計算機的第 5 回合
| 排 | 1 | 2 | 4 | 8 | 16 |
| 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 3 | 1 | 1 | 0 | 0 | 0 |
| 3 | 1 | 1 | 0 | 0 | 0 |
| 全部的 | 2 | 4 | 0 | 0 | 0 |
接下來的幾步,我讓計算機繼續按照 x,x,y,y 的模式走。這裡計算機給我的結果是 2,2,3,2;所以我留給它的是 2,2,2,2。

然後計算機給了我2,2,1,2。我留下2,2,1,1。
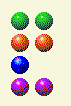
然後計算機給我的結果是2,2,1。我給它留下的是2,2。如果你能把對手的棋子分成兩行,你就贏了,只要保持兩行棋子相等就行了。

然後計算機給我留下一堆 2,然後我拿走 1。

遊戲到此結束。
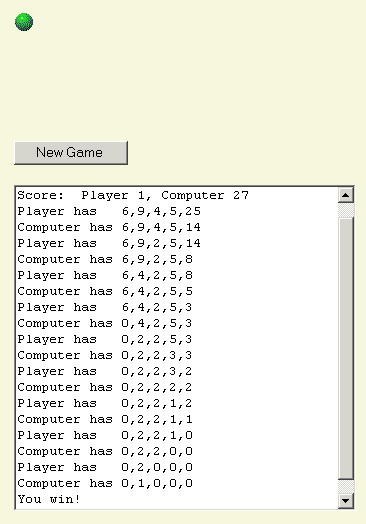
我最近得到了一個嘉年華輪盤,是我叔祖父的,大概有一百年歷史了。我正在嘗試用它來開發一個遊戲。輪盤上的數字從1到60隨機排列,每隔十五個標記就會出現一個綠色的星星,黑色和紅色交替出現。您能幫我估算一下每次旋轉的賠率嗎?
因此,有30個黑色號碼、30個紅色號碼和4個綠色號碼。這樣,黑色中獎的機率為30/64,紅色中獎的機率為30/64,綠色中獎的機率為4/64。如果某個事件的機率為p,則公平賠率為(1-p)/p比1。因此,任何紅色號碼的公平賠率為(34/64)/(30/64) = 34比30 = 17比15。黑色號碼的公平賠率為(60/64)/(4/64) = 60比4 = 15比1。對於特定號碼,公平賠率為(63/64)/(1/64) = 63比1。
我建議紅黑投注賠率為1比1,綠色投注賠率為14比1,任何單一數字的賠率為60比1。賭場優勢的一個公式是(ta)/(t+1),其中t是真實賠率,a是實際賠率。在本例中,投注紅色或黑色的賭場優勢為(63-60)/(63+1) = 3/64 = 4.69%。投注綠色的賭場優勢為(15-14)/(15+1) = 1/16 = 6.25%。投注單一數字的賭場優勢為(63-60)/(63+1) = 3/64 = 4.69%。
在紐約州,場外投注點設有視訊彩票終端機 (VLT)。當一台視訊彩票機「熱身」並連續發出一手好牌時,你會聽到「機器接近其「設定點」」的說法。這就能解釋為什麼同一台機器有時能贏,有時卻不贏。而且,大多數這類機器不允許你輸掉一手好牌。如果你輸掉一手好牌,它就會給你等值或更好的牌。你對此有什麼看法?
VLT 是美化的拉片遊戲。它有一個預先設定的結果池。當你玩的時候,遊戲會從結果池中隨機選擇一個結果,並以老虎機或視訊撲克遊戲的形式向玩家顯示獲勝結果。由於結果是注定的,任何技巧因素都是虛構的。例如,如果你拿到了同花大順,然後把它丟掉,你抽牌時會再得到一張。我通常說,在賭博中過去並不重要,但在這種情況下,存在著「消除效應」。如果你玩了一次輸了,那麼它會略微提高剩餘遊戲結果的賠率,直到虛擬拉片的供應耗盡,我猜虛擬轉盤會被重新填滿。我相信你的忽冷忽熱只是正常的運氣,任何宿命都是想像出來的。
後來,一位讀者在該主題中添加了以下內容。
我對你2月14日的「問巫師」專欄(第183期)有一點看法。其實這跟你回答的問題沒什麼關係,但你可能會覺得有趣而已。
在1A提案通過(允許全面開展3類博彩)之前,我們曾安裝過幾年小型的VLT系統。我們的系統由SDG(現為Bally的一部分)運營,獎金池初始為400萬次抽獎。當獎金池縮減至200萬時,我們又增加了一個400萬的獎金池,使總獎金池達到600萬次抽獎。當獎金池再次縮減至200萬時,我們又重複了這個過程。
贏得 Yahtzee 需要預計擲幾次?
假設玩家總是持有出現次數最多的數字,則平均值為11.09。下表顯示了在8,260萬次隨機模擬試驗中,擲骰次數的分佈。
骰子實驗
| 麵包捲 | 發生 | 可能性 |
| 1 | 63908 | 0.00077371 |
| 2 | 977954 | 0.0118396 |
| 3 | 2758635 | 0.0333975 |
| 4 | 4504806 | 0.0545376 |
| 5 | 5776444 | 0.0699327 |
| 6 | 6491538 | 0.0785901 |
| 7 | 6727992 | 0.0814527 |
| 8 | 6601612 | 0.0799227 |
| 9 | 6246388 | 0.0756221 |
| 10 | 5741778 | 0.0695131 |
| 11 | 5174553 | 0.0626459 |
| 12 | 4591986 | 0.0555931 |
| 十三 | 4022755 | 0.0487016 |
| 14 | 3492745 | 0.042285 |
| 15 | 3008766 | 0.0364257 |
| 16 | 2577969 | 0.0312103 |
| 17 | 2193272 | 0.0265529 |
| 18 | 1864107 | 0.0225679 |
| 19 | 1575763 | 0.019077 |
| 20 | 1329971 | 0.0161013 |
| 21 | 1118788 | 0.0135446 |
| 22 | 940519 | 0.0113864 |
| 23 | 791107 | 0.00957757 |
| 24 | 661672 | 0.00801056 |
| 二十五 | 554937 | 0.00671837 |
| 二十六 | 463901 | 0.00561624 |
| 二十七 | 387339 | 0.00468933 |
| 二十八 | 324079 | 0.00392347 |
| 二十九 | 271321 | 0.00328476 |
| 三十 | 225978 | 0.00273581 |
| 31 | 189012 | 0.00228828 |
| 三十二 | 157709 | 0.00190931 |
| 33 | 131845 | 0.00159619 |
| 三十四 | 109592 | 0.00132678 |
| 三十五 | 91327 | 0.00110565 |
| 三十六 | 76216 | 0.00092271 |
| 三十七 | 63433 | 0.00076795 |
| 三十八 | 52786 | 0.00063906 |
| 三十九 | 44122 | 0.00053417 |
| 40 | 36785 | 0.00044534 |
| 41 | 30834 | 0.00037329 |
| 四十二 | 25494 | 0.00030864 |
| 43 | 21170 | 0.0002563 |
| 四十四 | 17767 | 0.0002151 |
| 45 | 14657 | 0.00017745 |
| 46 | 12410 | 0.00015024 |
| 四十七 | 10299 | 0.00012469 |
| 四十八 | 8666 | 0.00010492 |
| 49 | 7355 | 0.00008904 |
| 50 | 5901 | 0.00007144 |
| 51 | 5017 | 0.00006074 |
| 52 | 4227 | 0.00005117 |
| 53 | 3452 | 0.00004179 |
| 54 | 2888 | 0.00003496 |
| 55 | 2470 | 0.0000299 |
| 56 | 2012 | 0.00002436 |
| 57 | 1626 | 0.00001969 |
| 58 | 1391 | 0.00001684 |
| 59 | 1135 | 0.00001374 |
| 60 | 924 | 0.00001119 |
| 61 | 840 | 0.00001017 |
| 62 | 694 | 0.0000084 |
| 63 | 534 | 0.00000646 |
| 64 | 498 | 0.00000603 |
| 65 | 372 | 0.0000045 |
| 66 | 316 | 0.00000383 |
| 67 | 286 | 0.00000346 |
| 68 | 224 | 0.00000271 |
| 69 | 197 | 0.00000238 |
| 70 | 160 | 0.00000194 |
| 71 | 125 | 0.00000151 |
| 72 | 86 | 0.00000104 |
| 73 | 79 | 0.00000096 |
| 74 | 94 | 0.00000114 |
| 75 | 70 | 0.00000085 |
| 76 | 64 | 0.00000077 |
| 77 | 三十八 | 0.00000046 |
| 78 | 四十二 | 0.00000051 |
| 79 | 二十七 | 0.00000033 |
| 80 | 33 | 0.0000004 |
| 81 | 16 | 0.00000019 |
| 82 | 18 | 0.00000022 |
| 83 | 19 | 0.00000023 |
| 84 | 14 | 0.00000017 |
| 85 | 6 | 0.00000007 |
| 86 | 4 | 0.00000005 |
| 87 | 9 | 0.00000011 |
| 88 | 4 | 0.00000005 |
| 89 | 5 | 0.00000006 |
| 90 | 5 | 0.00000006 |
| 91 | 1 | 0.00000001 |
| 92 | 6 | 0.00000007 |
| 93 | 1 | 0.00000001 |
| 94 | 3 | 0.00000004 |
| 95 | 1 | 0.00000001 |
| 96 | 1 | 0.00000001 |
| 97 | 2 | 0.00000002 |
| 102 | 1 | 0.00000001 |
| 全部的 | 82600000 | 1 |
您是否知道任何網站對西洋雙陸棋的賠率/統計數據/機率有很好的分析?您是否可以推薦有關該遊戲任何方面的特定書籍?
西洋雙陸棋是我最喜歡的賭博遊戲之一。我沒有寫過關於它的文章,因為玩家對戰遊戲極為難分析。而且我似乎也找不到任何可以突破的玩法。所以,我還是把建議留給其他人吧。以下是我推薦的資源:
保羅‧馬格里爾的《西洋雙陸棋》 :如果說西洋雙陸棋有一本聖經,那一定是這本了。我驕傲地擁有一本老精裝版。這本書會是很好的入門書。雖然這本書寫於1976年,但其中的建議仍然適用。
比爾羅伯蒂的《501道西洋雙陸棋基本題》 :多年來我一直想通讀這本書,但到現在才完成了一半。一半的題目都答錯,真是令人沮喪,甚至讓我覺得自己玩西洋雙陸棋就像打高爾夫一樣糟糕。然而,每錯一道題,都蘊藏著寶貴的經驗教訓。對中高級棋手來說,這本書是一本寶貴的學習工具,能讓人謙卑下來。
Snowie 西洋雙陸棋軟體:我每年用它下大約1000盤。 Snowie 不僅棋藝近乎完美,還能精準地告訴你失誤的代價有多大。它還有很多我從未探索過的功能。如果我從 Snowie 身上學到了什麼,那就是我最大的問題在於,有時我看不清明顯的走法,因而犯下愚蠢的錯誤。就像下棋一樣,一步錯棋就能毀掉一百步好棋。
Motif 網址:在購買 Snowie 之前,我和 Motif 打過無數盤。在我看來,Motif 的策略非常紮實。沒有什麼比與更強大的對手比賽更能提升自己的水準了。
在2004年4月11日的專欄中,有一個關於「價格合適」展示攤牌中正確策略的問題。假設遵循最佳策略,那麼每個玩家獲勝的機率是多少?
下表顯示了每位玩家的獲勝機率,根據第一位玩家的首次旋轉,玩家1先出,然後是玩家2,玩家3最後出。最下面一行顯示了首次旋轉前的整體獲勝機率。
價格合適的展示攤牌中的機率
| 旋轉 1 | 策略 | 玩家 1 | 玩家 2 | 玩家 3 |
| 0.05 | 旋轉 | 20.59% | 37.55% | 41.85% |
| 0.10 | 旋轉 | 20.59% | 37.55% | 41.86% |
| 0.15 | 旋轉 | 20.57% | 37.55% | 41.87% |
| 0.20 | 旋轉 | 20.55% | 37.55% | 41.9% |
| 0.25 | 旋轉 | 20.5% | 37.56% | 41.94% |
| 0.30 | 旋轉 | 20.43% | 37.56% | 42.01% |
| 0.35 | 旋轉 | 20.33% | 37.58% | 42.10% |
| 0.40 | 旋轉 | 20.18% | 37.60% | 42.22% |
| 0.45 | 旋轉 | 19.97% | 37.64% | 42.39% |
| 0.50 | 旋轉 | 19.68% | 37.71% | 42.61% |
| 0.55 | 旋轉 | 19.26% | 37.81% | 42.93% |
| 0.60 | 旋轉 | 18.67% | 37.96% | 43.36% |
| 0.65 | 旋轉 | 17.86% | 38.21% | 43.93% |
| 0.70 | 停留 | 21.56% | 38.28% | 40.16% |
| 0.75 | 停留 | 28.42% | 35.21% | 36.38% |
| 0.80 | 停留 | 36.82% | 31.26% | 31.92% |
| 0.85 | 停留 | 46.99% | 26.35% | 26.66% |
| 0.90 | 停留 | 59.17% | 20.36% | 20.47% |
| 0.95 | 停留 | 73.61% | 13.19% | 13.21% |
| 1.00 | 停留 | 90.57% | 4.72% | 4.72% |
| 平均的 | 30.82% | 32.96% | 36.22% |
以下是 6×20 6 種可能組合中的獲勝數。
玩家 1:118,331,250玩家2:126,566,457
玩家3:139,102,293
按照你的玩法,第三張牌匹配為平局,如果前兩張牌之間至少有六個點數差(六張牌差),賠率就會對你有利。我在橘郡玩的時候,第三張牌配對的結果是雙輸。根據這條規則,八張牌差的賠率是收支平衡的。如果第三張牌配對的結果是一倍輸,那麼你需要七張牌差的賠率才能對你有利。
單張撲克遊戲有三張牌,一張 A、一張 2 和一張 3。 A 最小,3 最大。兩位玩家各向底池下注 1 美元。然後,每位玩家拿到一張牌。下注順序是預先決定的,玩家 1 先行動。玩家 1 可以下注 1 美元或過牌。如果玩家 1 下注,玩家 2 可以跟注或棄牌。如果玩家 1 過牌,那麼玩家 2 可以下注 1 美元或過牌。如果玩家 1 過牌,玩家 2 下注,那麼玩家 1 可以跟注或棄牌。如果兩位玩家都過牌或都下注,那麼牌值較大的玩家贏得底池。假設兩位玩家都是完美的邏輯學家,那麼每位玩家的最佳策略是什麼?
希望你滿意;我花了一整天研究這個問題。答案和解答可以在我的另一個網站mathproblems.info上的第 203 題找到,或者在 Jason Swanson 的學術論文《博弈論與撲克》中找到。
我正在四處尋找抵押貸款。某公司提供的30年期固定利率貸款利率為5.75%,另加一個點。另一家公司提供的利率為5.875%,不加點。哪家公司比較划算?
為了方便其他讀者理解,點數指的是貸款收取的佣金。例如,一筆25萬美元的貸款,一個點數就是2,500美元。我假設借款人會把這個點數加到本金餘額中,並且絕對不會提前償還本金。
下表為以一個點的利率和期限計算的無點等值利率。
無點數的等值利率
| 一點利率 | 10年 | 15年 | 20年 | 30年 | 40年 |
| 4.00% | 4.212% | 4.147% | 4.115% | 4.083% | 4.067% |
| 4.25% | 4.463% | 4.398% | 4.366% | 4.334% | 4.318% |
| 4.50% | 4.714% | 4.649% | 4.617% | 4.585% | 4.570% |
| 4.75% | 4.965% | 4.900% | 4.868% | 4.836% | 4.821% |
| 5.00% | 5.216% | 5.151% | 5.119% | 5.088% | 5.073% |
| 5.25% | 5.467% | 5.402% | 5.370% | 5.339% | 5.324% |
| 5.50% | 5.718% | 5.654% | 5.621% | 5.590% | 5.576% |
| 5.75% | 5.969% | 5.905% | 5.873% | 5.842% | 5.827% |
| 6.00% | 6.220% | 6.156% | 6.124% | 6.093% | 6.079% |
| 6.25% | 6.471% | 6.407% | 6.375% | 6.344% | 6.330% |
| 6.50% | 6.723% | 6.658% | 6.626% | 6.596% | 6.582% |
| 6.75% | 6.974% | 6.909% | 6.878% | 6.847% | 6.834% |
| 7.00% | 7.225% | 7.160% | 7.129% | 7.099% | 7.085% |
| 7.25% | 7.476% | 7.412% | 7.380% | 7.350% | 7.337% |
| 7.50% | 7.727% | 7.663% | 7.631% | 7.602% | 7.589% |
| 7.75% | 7.978% | 7.914% | 7.883% | 7.853% | 7.841% |
| 8.00% | 8.229% | 8.165% | 8.134% | 8.105% | 8.093% |
| 8.25% | 8.480% | 8.416% | 8.385% | 8.357% | 8.344% |
| 8.50% | 8.731% | 8.668% | 8.637% | 8.608% | 8.596% |
| 8.75% | 8.982% | 8.919% | 8.888% | 8.860% | 8.848% |
| 9.00% | 9.233% | 9.170% | 9.140% | 9.112% | 9.100% |
| 9.25% | 9.485% | 9.421% | 9.391% | 9.363% | 9.352% |
| 9.50% | 9.736% | 9.673% | 9.642% | 9.615% | 9.604% |
| 9.75% | 9.987% | 9.924% | 9.894% | 9.867% | 9.856% |
| 10.00% | 10.238% | 10.175% | 10.145% | 10.119% | 10.108% |
這表明,5.75% 的利率加上一個點,相當於 5.842% 的利率(沒有點)。換句話說,假設收取的點數加到本金餘額中,兩種情況的還款金額相同。您的另一個報價是 5.875% 的利率(沒有點數),高於 5.842%,所以我會選擇 5.75% 的利率(加上點數)。
PS 對於那些想知道我如何解 i 的人,我使用了 Excel 中的速率函數。
我兒子兩週內剛打出兩個一桿進洞。這幾率是多少?我兒子的差點是1。第一個洞151碼,第二洞137碼,在兩個不同的球場。
根據 Gregory Baer 所著的《人生:機率(以及如何提高機率)》 ,在 PGA 巡迴賽中,在標準桿 3 杆洞中一桿進洞的機率是 2491 分之一。我相信這些距離都屬於標準桿 3 桿範圍內。
1差點已經很不錯了,所以跟美巡賽球員相比,我不會打太大折扣。假設你兒子每桿3桿洞的機率是3000分之一。一個典型的高爾夫球場大約有四個3桿洞。假設你兒子每天都打球,那麼他一週要打28個3桿洞。那麼剛好打出兩個一桿進洞的機率就是 (28,2)×(1/3000) ² ×(2999/3000) ²² =24017分之一。
我最近參加了一個抽獎活動,獎品有7033個,據說中獎機率是1/13。我買了5張彩券。我實際中獎機率是多少?另外,大獎有40個。我中大獎的機率是多少?
為了簡單起見,我們忽略這樣一個事實:你買的彩票越多,每張彩票的價值就越低,因為你正在與自己競爭。也就是說,輸掉五張彩券的機率是 (12/13) 5 = 67.02%。所以至少贏得一次獎的機率是 32.98%。在你買彩券之前,彩券桶裡總共有 7033×13=91,429 張彩券。 91,429-40=91,389 張彩券不是大獎。五張彩券中不了大獎的機率是 (91,389/91429) 5 = 99.78%。所以至少贏得一次大獎的機率是 0.22%,也就是 458 分之一。
在紅桃遊戲中,每位玩家有13張牌。其中牌數最多的花色稱為“長花”,其花色可以是4到13張。這些花色總數的機率是多少?
紅桃長花的機率
| 牌 | 組合 | 可能性 |
| 4 | 222766089260 | 0.35080524800183 |
| 5 | 281562853572 | 0.44339660045899 |
| 6 | 105080049360 | 0.16547685914958 |
| 7 | 22394644272 | 0.03526640326564 |
| 8 | 2963997036 | 0.00466761219692 |
| 9 | 235237860 | 0.00037044541245 |
| 10 | 10455016 | 0.00001646424055 |
| 11 | 231192 | 0.00000036407412 |
| 12 | 2028 | 0.00000000319363 |
| 十三 | 4 | 0.00000000000630 |
| 全部的 | 635013559600 | 1 |
72法則指的是,用年報酬率除以72,就能算出你的資金翻倍所需的年數。例如,一項年回報率為10%的投資,需要72/10=7.2年才能翻倍。我有個有點無聊的問題:為什麼要72年?
首先,「72法則」只是資金翻倍所需時間的近似估計,而非確切答案。下表列出了不同年利率下「72法則」的數值以及確切的翻倍年數。
72法則-金錢翻倍的年限
| 利率 | 72法則 | 精確的 | 不同之處 |
|---|---|---|---|
| 0.01 | 72.00 | 69.66 | 2.34 |
| 0.02 | 36.00 | 35.00 | 1.00 |
| 0.03 | 24.00 | 23.45 | 0.55 |
| 0.04 | 18.00 | 17.67 | 0.33 |
| 0.05 | 14.40 | 14.21 | 0.19 |
| 0.06 | 12.00 | 11.90 | 0.10 |
| 0.07 | 10.29 | 10.24 | 0.04 |
| 0.08 | 9.00 | 9.01 | -0.01 |
| 0.09 | 8.00 | 8.04 | -0.04 |
| 0.10 | 7.20 | 7.27 | -0.07 |
| 0.11 | 6.55 | 6.64 | -0.10 |
| 0.12 | 6.00 | 6.12 | -0.12 |
| 0.13 | 5.54 | 5.67 | -0.13 |
| 0.14 | 5.14 | 5.29 | -0.15 |
| 0.15 | 4.80 | 4.96 | -0.16 |
| 0.16 | 4.50 | 4.67 | -0.17 |
| 0.17 | 4.24 | 4.41 | -0.18 |
| 0.18 | 4.00 | 4.19 | -0.19 |
| 0.19 | 3.79 | 3.98 | -0.20 |
| 0.20 | 3.60 | 3.80 | -0.20 |
為什麼是 72?不一定要剛好是 72。這只是一個與實際投資利率相符的數字。它幾乎恰好對應於 7.8469% 的利率。 72 本身並沒有什麼特別之處,就像 π 或 e 一樣。為什麼任何數字都可以呢?假設利率是 i,那麼我們來計算一下投資翻倍所需的年數 (y)。
2 = (1+i) y
ln(2)= ln(1+i) y
ln(2)= y×ln(1+i)
y = ln(2)/ln(1+i)
這可能不是我迄今為止最好的答案,但請嘗試遵循這個邏輯:讓 y=ln(x)。
dy/dx=1/x。
當 x 的值接近 1 時,1/x =~ x。
因此,當 x 值接近 1 時,dy/dx =~ 1。
因此,當 x 值接近 1 時,ln(x) 的斜率將接近 1。
因此,當 x 值接近 0 時,ln(1+x) 的斜率將接近 1。
「72 法則」指 .72/i =~ .6931/ln(1+i)。
我們已經確定,當 i 的值接近 0 時,i 和 ln(1+i) 相似。
因此,當 i 的值接近 0 時,1/i 和 1/ln(1+i) 相似。
使用 72 而不是 69.31 可以調整 i 和 ln(1+i) 之間的差異,使 i 的值在 8% 左右。
希望你理解得通。我的微積分學得有點生疏,我花了好幾個小時才解釋清楚。
這個問題是在我的同伴網站Wizard of Vegas的論壇中提出並討論的。
最近在一次街頭市集上,他們玩了一個遊戲,裡面有一塊數字區域,裡面有一些淺杯子和一個裝滿球的杯子,遊戲涉及加法。我沒有問這個遊戲的名字,在網路上搜尋了大約一個小時,但什麼也沒找到。我以為你可能有一些關於它的訊息,例如它的機率,或至少知道它的名字。
這款遊戲的行業術語是Razzle Dazzle。我記得小時候在南加州見過,去年在墨西哥聖費利佩也見過。它通常被設計成看起來像一場足球比賽。在我看來,這款遊戲是嘉年華遊戲騙局中最惡劣的。紐約州應該為允許這種遊戲而感到羞恥。根據一些研究,雖然各個地方的規則各不相同,但騙局的本質總是一樣的。
它基於與擲骰子遊戲中的“場地投注”相同的原理。對於那些不熟悉「場地投注」的讀者來說,如果兩顆骰子擲出的總點數為2、3、4、9、10、11或12,玩家就贏了。輸的點數為5、6、7和8。贏的賠率相同,但擲出2的賠率為2比1,擲出12的賠率為3比1(在吝嗇的哈拉斯賭場除外,那裡只有擲出12的賠率為2比1)。數學能力較弱的賭徒可能會錯誤地認為這是一個不錯的賭注,因為有7個點數會贏,只有4個點數會輸。賠率對賭場有利的原因是,擲輸的點數的可能性最大。
以下是 Razzle Dazzle 的具體規則,摘自唐納德·A·貝裡 (Donald A. Berry) 和羅納德·R·瑞格爾 (Ronald R. Regal) 撰寫的《贏得某場嘉年華遊戲的概率》一文,該文發表在 1978 年 11 月的《美國統計學家》雜誌上。
- 遊戲的目標是在足球場上前進100碼。玩家完成目標後將獲得一些獎勵。
- 玩家每次玩時開始支付指定的費用,例如 1 美元。
- 玩家將把 8 顆彈珠投擲到 11 x 13 的格子上。每顆彈珠都會掉入 143 個孔中的一個。
- 每個洞都有 1 到 6 的點數。下表顯示了每個點數的頻率。
Razzle Dazzle 積分分配
積分 數位
在船上可能性 1 11 0.076923 2 19 0.132867 3 三十九 0.272727 4 四十四 0.307692 5 19 0.132867 6 11 0.076923 全部的 143 1.000000 - 總分將被累加。裁判員會在換算表上找出總分,以計算出選手前進了多少碼。換算表如下圖所示。
Razzle Dazzle轉換表
積分 碼
獲得8 100 9 100 10 50 11 三十 12 50 十三 50 14 20 15 15 16 10 17 5 18至38歲 0 三十九 5 40 5 41 15 四十二 20 43 50 四十四 50 45 三十 46 50 四十七 100 四十八 100 - 如果玩家擲出的總點數為 29,則所有後續擲骰的費用將翻倍,並且當玩家到達足球場的另一端時,他將獲得一個額外的獎品。
每顆彈珠的平均得分為 3.52 分,標準差為 1.31。請注意,3 分和 4 分的機率最高。這使得標準差保持在較低水平,並且多顆彈珠的總得分接近預期。相比之下,單一骰子擲出的標準差為 1.71。
接下來,請注意碼數轉換表上總共有20個獲勝結果和21個失敗結果。那些在嘉年華遊戲上賭博的傻瓜可能會錯誤地認為他們的晉級機率是20/41或48.8%。如果嘉年華工作人員謊稱這是晉級機率,我一點也不會感到驚訝。然而,就像場地投註一樣,最有可能的結果並不會贏任何東西。
下表顯示了每回合得分、碼數和預期碼數的機率。右下角單元格顯示每回合平均碼數為0.0196。
每回合預計獲得碼數
| 積分 | 可能性 | 碼 獲得 | 預期的 碼 獲得 |
| 8 | 0.00000000005 | 100 | 0.00000000464 |
| 9 | 0.00000000176 | 100 | 0.00000017647 |
| 10 | 0.00000002586 | 50 | 0.00000129285 |
| 11 | 0.00000022643 | 三十 | 0.00000679305 |
| 12 | 0.00000143397 | 50 | 0.00007169849 |
| 十三 | 0.00000713000 | 50 | 0.00035650022 |
| 14 | 0.00002926510 | 20 | 0.00058530196 |
| 15 | 0.00010234709 | 15 | 0.00153520642 |
| 16 | 0.00031168305 | 10 | 0.00311683054 |
| 17 | 0.00083981462 | 5 | 0.00419907311 |
| 18 | 0.00202563214 | 0 | 0.00000000000 |
| 19 | 0.00441368617 | 0 | 0.00000000000 |
| 20 | 0.00874847408 | 0 | 0.00000000000 |
| 21 | 0.01586193216 | 0 | 0.00000000000 |
| 22 | 0.02642117465 | 0 | 0.00000000000 |
| 23 | 0.04056887936 | 0 | 0.00000000000 |
| 24 | 0.05757346716 | 0 | 0.00000000000 |
| 二十五 | 0.07566411880 | 0 | 0.00000000000 |
| 二十六 | 0.09221675088 | 0 | 0.00000000000 |
| 二十七 | 0.10431970222 | 0 | 0.00000000000 |
| 二十八 | 0.10958441738 | 0 | 0.00000000000 |
| 二十九 | 0.10689316272 | 0 | 0.00000000000 |
| 三十 | 0.09677806051 | 0 | 0.00000000000 |
| 31 | 0.08125426057 | 0 | 0.00000000000 |
| 三十二 | 0.06317871335 | 0 | 0.00000000000 |
| 33 | 0.04540984887 | 0 | 0.00000000000 |
| 三十四 | 0.03009743061 | 0 | 0.00000000000 |
| 三十五 | 0.01833921711 | 0 | 0.00000000000 |
| 三十六 | 0.01023355162 | 0 | 0.00000000000 |
| 三十七 | 0.00520465303 | 0 | 0.00000000000 |
| 三十八 | 0.00239815734 | 0 | 0.00000000000 |
| 三十九 | 0.00099365741 | 5 | 0.00496828705 |
| 40 | 0.00036673565 | 5 | 0.00183367827 |
| 41 | 0.00011909673 | 15 | 0.00178645089 |
| 四十二 | 0.00003349036 | 20 | 0.00066980729 |
| 43 | 0.00000797528 | 50 | 0.00039876403 |
| 四十四 | 0.00000155945 | 50 | 0.00007797235 |
| 45 | 0.00000023832 | 三十 | 0.00000714969 |
| 46 | 0.00000002632 | 50 | 0.00000131607 |
| 四十七 | 0.00000000176 | 100 | 0.00000017647 |
| 四十八 | 0.00000000005 | 100 | 0.00000000464 |
| 總計 | 1.00000000000 | 0 | 0.01961648451 |
以下是對 1750 萬場遊戲進行隨機模擬的一些結果。
Razzle Dazzle 模擬結果
| 問題 | 回答 |
| 每回合晉級的機率 | 0.0028 |
| 預計每回合獲得碼數 | 0.0196 |
| 每次推進預計獲得碼數 | 6.9698 |
| 每場比賽預期回合數 | 5238.7950 |
| 每場比賽平均雙打數 | 559.9874 |
| 每場比賽平均獎金 | 560.9874 |
我本來想指出每場遊戲的平均總投注額,但我的電腦無法處理這麼大的數字。在平均每場5239輪的遊戲中,玩家平均加倍投注560次。模擬中的一局遊戲,玩家加倍投注1800次。即使平均加倍560次,假設起始投注額為1美元,每輪的投注額也高達3.77×10^ 168美元。這比已知宇宙中的原子數量還要大幾個數量級(來源)。
即使是最幼稚的玩家,如果每355次才晉級一次,也玩不了多久。嘉年華工作人員一開始會做的就是為了玩家好而作弊。他們可能會發現玩家有免費擲骰子的機會,或者在加分時撒謊,讓玩家贏取總分,以增強他們的信心。我從未玩過這個遊戲,但我猜想,當玩家接近紅區(距離觸地得分20碼或更短)時,嘉年華工作人員就會開始公平地比賽。玩家可能會想知道為什麼自己突然一無所獲,但既然已經投入了資金,而且距離終點線如此之近,他肯定不會輕易放棄,放棄已經支付的碼數。
連結
- 《Razzle Dazzle》 ,摘自《On the Midway》一書。
- Razzle Dazzle Carny 桌遊街機騙局。
- 唐納德·A·貝里和羅納德·R·里格爾合著的《贏得某場嘉年華遊戲的機率》
最近的一個嘉年華推出了一款井字棋遊戲。遊戲售價1英鎊,玩家需要將三個彈力十足的球丟向一個底部有9個格子的大木箱。假設每個球都落在不同的格子裡,那麼獲勝的機率是多少?
有八種獲勝方式:三行、三列和兩條對角線。從 9 個方格中抽出 3 個,一共有(9,3)=84 種組合方式。因此獲勝機率為 8/84 = 9.52%。
這個問題是在我的同伴網站Wizard of Vegas的論壇中提出並討論的。
您對玩大富翁遊戲有什麼建議?
這是我的巫師玩大富翁遊戲的基本策略:
- 買下所有東西。如果房產無法幫助你壟斷、阻止他人,或作為籌碼的價值不高,高級玩家可能會破例。在資金短缺的情況下,公共設施也可能被拒絕。
- 盡可能地交易。這就是技巧的用武之地。盡量交易你能交易到的最佳套裝。我通常會將它們按以下順序排列:橙色、黃色、淺藍色、深藍色、淺紫色、紅色、綠色、深紫色。具體順序會根據具體情況而有所不同。在資金緊張的遊戲中,優先選擇開發成本較低的套裝,例如淺藍色套裝。在資金充裕的遊戲中,選擇那些更有可能花錢購買的套裝,例如黃色或深藍色套裝。
- 一旦你擁有一套房產,無論是自然而然的還是透過交易獲得的,都要迅速累積。盡量盡快在每處房產上蓋三棟房子。三棟之後,每棟房子的邊際報酬率就會下降。把大部分其他房產抵押出去,把現金花掉。你應該留下一點淨資產來應付一些小開支。不花錢就像戰場上的士兵不用子彈一樣。
- 反對所有愚蠢的規則。尤其要反對「免費停車」的獎金池(我受不了那個!)。如果你比對手更熟練,你就應該盡量減少遊戲的隨機性。
如果一隻猴子在玩魔術方塊,那麼在任意給定時間,它處於解出的圖案中的機率是多少?
魔術方塊的六個中心面是固定的。旋轉這些面只能重新排列角和棱。如果將魔術方塊拆開,那麼無論每個部分的方向如何,八個角的排列方式就有 8!=40,320 種。同樣,無論方向如何,十二條稜的排列方式也有 12!=479,001,600 種。
每個角有 3 種方向,總共有 3 8 = 6,561 種角方向。同樣,每個邊塊有兩種方向,總共有 2 12 = 4,096 種邊方向。
所以,如果我們把魔術方塊拆開,重新排列稜角,那麼就會有 8! × 12! × 3 8 × 2 12 = 519,024,039,293,878,000,000 種可能的排列組合。然而,並非所有這些排列組合都能透過旋轉面從起始位置得到。
首先,不可能只旋轉一個角,而其他部分保持不變。任何旋轉組合都無法做到這一點。基本上,每個動作都必須有一個反應。如果你想旋轉一個角,它會以某種方式乾擾其他棋子。同樣,也不可能只翻轉一個邊棋子。基於這些原因,我們必須將排列數除以 3 × 2 = 6。
其次,在不干擾魔術方塊其他部分的情況下,不可能交換兩個邊塊。這是這個答案中最難解釋的部分。魔術方塊所能做的就是每次旋轉一個面。每次轉動都會旋轉四個邊塊和四個角塊,總共移動八個塊。一系列旋轉可以用能被 8 整除的方塊移動次數來表示。通常,一系列移動會導致兩個移動相互抵消。但是,任何旋轉序列都會移動偶數個區塊。交換兩個邊塊需要一個移動次數,即奇數次,這不能透過任何偶數集的總和來實現。數學家稱之為奇偶校驗問題。因此我們必須再除以 2,因為在不干擾其他塊的情況下無法交換兩個邊塊。
因此,魔術方塊的排列組合共有 3 × 2 × 2 = 12 種可能。如果你拆開一個魔術方塊,然後隨機地重新組裝,那麼有 1/12 的機率,它能夠被解開。因此,魔術方塊的排列組合總數為 8! × 12! × 3 (12) × 2 (12/12 ) = 43,252,003,274,489,900,000。如果有 70 億隻猴子(大約相當於世界人口)隨機玩魔術方塊,以每秒旋轉一次的速度,魔術方塊平均每 196 年就會經過一次解開的位置。
連結
我玩的是紅心大戰,拿到10張了。這機率是多少?
對於不熟悉紅心牌規則的人來說,遊戲一開始會給四位玩家各發13張牌。紅心花色對遊戲至關重要,所以你拿到多少張紅心也很重要。下表顯示了拿到0到13張紅心的機率。
13 張牌中出現 0 至 13 個紅心的機率
| 紅心 | 組合 | 可能性 | 逆 |
|---|---|---|---|
| 十三 | 1 | 0.0000000000016 | 1比635,013,559,600.0 |
| 12 | 507 | 0.0000000007984 | 1比1,252,492,228.0 |
| 11 | 57,798 | 0.0000000910185 | 10,986,773.9分之一 |
| 10 | 2,613,754 | 0.0000041160601 | 242,950.8分之1 |
| 9 | 58,809,465 | 0.0000926113531 | 10,797.8 分之一 |
| 8 | 740,999,259 | 0.0011669030492 | 1比857.0 |
| 7 | 5,598,661,068 | 0.0088166008164 | 1比113.4 |
| 6 | 26,393,687,892 | 0.0415639752774 | 1比24.1 |
| 5 | 79,181,063,676 | 0.1246919258321 | 1比8.0 |
| 4 | 151,519,319,380 | 0.2386080062219 | 1比4.2 |
| 3 | 181,823,183,256 | 0.2863296074662 | 1比3.5 |
| 2 | 130,732,371,432 | 0.2058733541286 | 1比4.9 |
| 1 | 50,840,366,668 | 0.0800618599389 | 1/12.5 |
| 0 | 8,122,425,444 | 0.0127909480376 | 78.2分之1 |
| 全部的 | 635,013,559,600 | 1.0000000000000 |
這個問題是在我的同伴網站Wizard of Vegas的論壇中提出並討論的。
對於那些仍然使用普通彩票(而非電子彩票)的賭場促銷活動,玩家需要在玩家櫃檯打印彩票,然後將其放入轉鼓中——在將彩票放入轉鼓之前,你們會彎曲/折疊彩票嗎?你認為彎曲的彩券被抽中的幾率比較大嗎?
希望你滿意。為了回答這個問題,我在Office Depot買了一大卷彩券。然後我把其中500張彩券放進一個紙袋裡,一半對折,大約90度角,另一半展開。之後,我請六位志工每人每次抽取40到60張彩票,並進行替換,同時我記錄結果。結果如下。
抽獎券實驗
| 主題 | 折疊 | 展開 | 全部的 |
|---|---|---|---|
| 1 | 二十五 | 二十五 | 50 |
| 2 | 三十八 | 22 | 60 |
| 3 | 二十五 | 15 | 40 |
| 4 | 三十四 | 16 | 50 |
| 5 | 二十七 | 23 | 50 |
| 6 | 二十六 | 24 | 50 |
| 全部的 | 175 | 125 | 300 |
因此,抽出的彩票中有 58.3% 被折疊了!
如果假設棄牌沒有影響,那麼這些結果將與預期相差2.89個標準差。假設棄牌不影響中獎機率,那麼獲得這麼多或更多棄牌彩券的機率為0.19%,即514分之一。
我想補充的是,那些匆忙抽獎的受試者更有可能抽到棄牌。而那些每次抽獎都小心謹慎的受試者,抽到棄牌的機率接近或接近一半一半。
所以,我的結論肯定是放棄它們。
有關此問題的討論,請訪問我在Wizard of Vegas 的論壇。