二十一點 - 基本策略(特定牌型)
Wiz,你真是個好人!你的賭博網站絕對是網路上最好的。作為一名精算師(ACAS),我很高興看到有人能充分發揮自己的數學技能。
我的問題是──既然允許後期投降,你還想在10點亮牌的情況下分8點嗎?我猜是的,但BJ中最難的玩法之一就是在10點亮牌的情況下分8點。
順便提一下,我剛在拉斯維加斯待了三天,如果你還沒去過,一定要試試拉斯維加斯俱樂部和世界上最自由的二十一點規則。 3張或4張牌可以加倍,6張牌<=21點自動贏,也可以晚點投降。六副牌,我估計莊家優勢是0.14%。感謝你們的辛勤付出!
謝謝你的讚美,吉姆。是的,即使有人建議你晚點投降,你還是應該分牌。即使分牌後不能加倍,你也應該拒絕投降。基於兩副牌的遊戲,分牌後不能加倍,那麼分牌8對10的預期值為-0.480673,比投降的-0.5要好。
儘管他們聲稱擁有“世界上最自由的二十一點規則”,但在馬蹄鐵賭場(Horseshoe)或金門賭場(Golden Gate)街對面,卻有更好的單副牌遊戲。拉斯維加斯俱樂部(Las Vegas Club)的六副牌才是真正對玩家不利的。別因為被他們的招牌蒙蔽而感到難過,我年輕時也曾上當受騙,那時我還不知道規則變化的後果。
更新:這個問題之後,拉斯維加斯俱樂部修改了規則,在他們所謂的「世界上最自由的二十一點規則」中,對二十一點的賠率是6比5。6比5甚至不能算作真正的二十一點遊戲。在任何普通的3比2遊戲中,你的賠率都要高得多,這種遊戲在其他地方很容易找到。
單副牌二十一點的牌是面朝下發的嗎?單副牌的一般規則是什麼?我知道您提到只有9-11或10-11點可以加倍,但您知道單副牌的分牌後加倍、莊家要牌軟17點等等的一般規則是什麼嗎?我是一個基礎策略型玩家,想了解單副牌的規則(我只玩過6副或8副牌),這樣我就可以從blackjackinfo.com網站取得完美的電子表格。非常感謝您的幫忙!
單副牌二十一點的規則通常很嚴格。牌面朝下發牌。加倍通常限制在9比11或10比11。莊家拿到軟17點後加倍,分牌後可能不准加倍。如果二十一點的賠率低於3比2(單副牌遊戲通常如此),請務必不要玩。
您可以在我的“拉斯維加斯巫師”網站上隨時查看拉斯維加斯相對較新的二十一點規則。
你的二十一點策略是,對A、10、9,你棄牌16。你說要用一對8來對付這些牌。我聽說一對8就是16,應該棄牌。你怎麼看?
如果莊家查看底牌,發現沒有黑傑克,那為什麼要用軟18對抗A呢?還有,為什麼不在11點時加倍呢?
在二十一點遊戲中,很少有簡單的答案。你必須考慮所有可能發生的情況,並根據機率權衡每個結果。最佳玩法是預期回報最大的玩法。根據我的二十一點附錄 9b ,在雙層牌局中,用軟 18 對抗 A 的預期回報是 -0.1004,停牌的預期回報是 -0.1005。因此,要牌只是稍微好一點。用 11 對抗 A 也是非常邊緣的玩法。實際上,在單層和雙層牌局中,它都取決於牌型,換句話說,取決於哪兩張牌的總數為 11 來決定如何出牌。但是,如果你不想記住與牌型相關的基本策略例外,那麼你應該在單層和雙層牌局中用 11 對抗 A 時加倍下注,並用四副或更多牌要牌。
嗨!我很喜歡你的網站!如果我拿到黑傑克,而莊家亮出一張A,我可以選擇贏等額的錢還是繼續玩。我該贏等額的錢還是繼續玩?
這是看待投保決策的另一種方式。投保等額賭注的預期回報顯然是 1.0 個單位的賭注。為簡單起見,我們假設一副牌的數量是無限的。莊家拿到黑傑克的機率是 4/13,否則是 9/13。如果莊家拿到黑傑克,你就推牌。如果沒有,那你就贏 1.5 個單位。不投保的預期值為 (4/13)*0 + (9/13)*(1.5) = 13.5/13 = 1.0384615,大於 1.0。因此,拒絕投保或等額賭注並繼續玩牌是更好的選擇。在實際遊戲中,如果牌組數量有限,賠率會更高,因為(你手中的)牌組中已經有一張 10,這降低了莊家拿到黑傑克的機率。
「你不可兩面下注。」——《賭博十誡》(第七條)
麥克,上次我去拉斯維加斯的時候,我認識的一位荷官說,他「正在考慮」在莊家拿到16點牌時停牌,而莊家拿到7點牌時,因為8張牌中只有5張能讓莊家自動獲勝。這個策略該如何實施呢?
這會是一個糟糕的玩法。例如,我的二十一點附錄 9B展示了用 10 和 6 張牌對抗莊家 7 點牌的兩種情況的回報。拿牌的預期損失為賭注的 39.6%。然而,停牌的預期損失為 47.89%。我無法輕易解釋為什麼拿牌比較好。你必須考慮所有可能發生的情況,用機率加權,然後取總和。總的來說,拿牌是兩種糟糕玩法中更好的選擇。
關於附錄6中提到的投降例外情況,我該如何將其更好地運用到統一遊戲的單副牌遊戲中,在面對A牌時提前投降?感謝你的幫助和很棒的網站。
謝謝你的讚美。在統一遊戲 (Unified Gaming) 的二十一點遊戲中,只有當莊家亮出 10 點時,你才應該使用附錄六。當莊家亮出 A 點時,統一遊戲 (Unified Gaming) 的基本策略沒有例外。
我剛從哥斯達黎加回來。他們給二十一點賠率是1比1。這對賭場來說值多少錢?如果我拿到21點,而莊家拿到3比6,我是不是應該加倍下注?畢竟我的賠率只有1比1。
請參閱我的拉米牌頁面,拉米牌是在哥斯達黎加流行的二十一點變體。
您好,我剛剛看了您的 Microgaming 二十一點基本策略卡。我注意到,在 7,7 點牌時,您建議玩家不要在 10 點牌時拿牌。這是為什麼?這是否會影響在 14 點牌時拿牌的建議?
在我所有的單副牌二十一點策略中,這都是正確的玩法。原因是拿到第三個7的機率只有2/49,大約是4.08%。相較之下,雙副牌的機率是6/101,也就是5.94%。由於贏莊家20的希望不大,最好是拿牌,或者如果可以的話投降。沒錯,這確實推翻了我之前建議的用14來對付10的建議。
我當荷官已經十年了,一直在努力擺脫這個職業。我數不清有多少次聽人說:「永遠假設底牌是10。」 你我都知道,這話不可能總是對的。我理解他們為什麼這麼說,但是,它真的就是10的機率有多大呢?如果荷官手上有A,你用讀卡機檢查牌型,發現不是黑傑克,你一定知道它不是10。那麼,你又該假設它是什麼呢?
我也不喜歡這個說法。它充其量只是個記憶工具,用來幫助人們記住,如果莊家有7到10的牌,就應該打硬牌。沒有一個簡單的經驗法則,適用於所有情況。
我在二十一點網站上研究你的附錄1時,發現了一些奇怪的事情。六副牌遊戲的基本策略(分牌後加倍,莊家在軟17點不動等等——所有常見的脫衣舞規則)規定,如果莊家拿到5,A,2可以加倍。然而,附錄中卻指出,如果玩家拿到A,4,莊家拿到4的預期回報會更高(拿牌的預期回報為0.1334,加倍的預期回報為0.126)。如果玩家拿到A,4,莊家拿到4,預期回報也更高(拿牌的預期回報為0.0593,加倍的預期回報為0.0584)。其他所有分牌和加倍都有效。這兩個例子是怎麼回事?提前致謝。
附錄1基於無限套牌。你提到的兩種牌型都是邊界牌型,牌組數量會影響哪種打法比較好。例如,A-4 對抗 4 時,用 26 副牌加倍,用 27 副牌要牌。 A-2 對抗 5 時,牌組數也介於 8 副牌到無限副牌之間。
身為BJ玩家,我常用10對著爆牌分牌。這個舉動的期望值是正數,但不如原地不動那麼有利可圖。你能告訴我這位朋友,在中立牌組中,分牌10比原地不動要差多少嗎?另外,很多BJ玩家會因為有人用10對著6分牌分牌而感到不滿,但他們自己也常用2或7對著10分牌分牌。你能解釋一下嗎?
我煞費苦心地寫了二十一點附錄 9A-9H 來解答這類問題。例如,在六副牌的遊戲中,如果莊家在軟 17 點停牌,您可以使用二十一點附錄 9G。從中可以看出,如果莊家拿到兩張 10 點,而莊家拿到 6 點,停牌的預期收益為 0.702826。在這種情況下,分牌的預期收益為 0.622165。因此,玩家停牌比分牌可以多贏 8.07%。不要太在意其他玩家在二十一點牌桌上的言行。
Wiz,這是一個關於莊家10點,8點分牌的問題。分牌在單手牌中是正確的玩法。但是,我認為對於典型的二十一點玩家來說,考慮到你要加倍下注,最好是停牌。為什麼要在賠率這麼低、遠低於平均的情況下加倍下注呢?畢竟,目標是最大化你的總回報(即所有投注的加權平均值)。請問您有什麼看法?
PS:您的網站很棒,橫幅廣告和側邊欄等廣告是可以理解的,但像彈出窗口和問題提示這樣的侵入性廣告試圖強迫您訪問另一個網站,在我看來有點過分了。
雖然這局牌勢均力敵,但停牌是第三糟糕的選擇。使用我的二十一點附錄9G,我們可以得到以下預期效益:
- 支架-.536853
- 命中 -.535361
- 拆分 -.474733
- 雙倍 -1.07022
分牌是最佳選擇,因為它能將牌局的總損失降至最低。加倍和分牌的預期收益是基於該牌局相對於初始下注的總收益。例如,如果你的初始下注為100美元,然後你分牌,所有因素加起來,總預期損失為47.47美元,低於不加註的預期損失53.69美元。
雙重曝光的牌表顯示,如果莊家有13-16點,就分牌10。這是否意味著你還要繼續分牌10?我曾經這樣做過,結果四手牌都低於18點,全部輸了。幸好當時我只是在某個網路遊戲網站上玩玩而已。
是的,只要你一直拿到10,就應該繼續分牌。玩一手牌輸了並不能證明什麼。必須雙向玩數百萬手牌,並將結果匯總起來,才能真正找到最佳玩法。
在四副牌的二十一點遊戲中,如果你用A對5或6分牌,然後你又拿到一張A,你應該加倍還是要牌? (目前不再討論分牌)我在不同的網站上得到了不同的答案。到目前為止,我看到一個網站在5和6時加倍,一個網站只在6時加倍,其他網站列出了所有情況下的分牌,我猜他們沒有考慮這種情況。另一個問題是,在四副牌的二十一點遊戲中,用10、2對4,一個網站列出了要牌。我想請您確認一下。
請記住,大多數賭場不允許您這樣做。但是,如果可以,您應該只在 6 上加倍。無論莊家是否拿到軟 17 點,這都是正確的。如果莊家在軟 17 點上停牌,那麼面對 5 點,拿牌的預期回報是 0.162849,加倍是 0.148228,所以拿牌是更好的玩法。面對 6 點,拿牌的預期回報是 0.189020,加倍是 0.196249。所以加倍是更好的玩法。您可以在我的二十一點附錄 9e中親自查看這些數字。關於您的另一個問題,是的,在 4 副牌的遊戲中,玩家應該拿 10.2 對抗 4,但前提是莊家在軟 17 點上停牌。我自己沒有列出 4 副牌基本策略例外,因為例外很少,而且差異很小。遵循這個例外情況,你每113396手就能贏更多單位,或者說,賭場優勢降低0.000882%。在我看來,不值得費心記住這個例外情況。
在您的二十一點附錄 6中,關於後期投降,您建議在莊家拿到 10 時投降 10+5 和 9+6。在統一遊戲的基本策略中,您建議在莊家拿到 10 時拿 15。我不明白為什麼在這種情況下要拿牌而不是投降,因為 9+6 和 10+5 比 8+7 更有可能拿到 15。
這是一個有趣的情況。雖然在單副牌中,15點對10點時你應該有5/6的機率投降,但總是要牌總比總是投降要好。以下是每次要牌湊成15點的預期收益。
- 10+5
- -.501091
- 9+6
- -.509827
- 8+7
- -.474794
有四種方法可以湊成10+5,而其他兩種方法各只有1種。因此,在一副牌中,若點數為15,而點數為10,則總預期報酬為 (4/6)*-.501091 + (1/6)*-.509827 + (1/6)*-.474794 = -.498164。換句話說,點數為10、5和9、6的機率略高,而點數為8、7的機率則高得多。 8、7的預期報酬率較高的原因是,牌堆裡仍然有5和6,因此點數為20或21的機率更大。
我的問題是關於BJ的賭桌最高下注額。假設官方公佈的下注額度是200美元。我下注200美元,拿到8-3的牌。我可以加倍嗎?或者,假設我下注200美元,拿到一對A。我可以把牌分成兩手嗎?
是的,在這種情況下,您可以加倍或分牌。最高限額適用於初始下注。如果限額為 200 美元,您也可以玩多手 200 美元的牌。
我剛剛讀到一篇文章,說在多副牌(4副或更多副牌)的二十一點遊戲中,如果莊家的牌是10,並且包含4或5,那麼正確的基本策略是停牌。我查看了你們的網站,發現只找到了單副牌和雙副牌遊戲中多張牌的附錄。這篇文章對嗎?
是的!好問題,連我都不知道這一點。牌堆越少,牌的數量越多,這種情況就越明顯。為了測試最有可能擊中的情況——8 副牌堆,只有 3 張牌——我用我的組合程序運行了所有可能的情況。下表顯示了結果。
8 副牌遊戲中 3 張牌 16 對 10 的預期值
| 手 | 電動車熱賣 | 電動車支架 | 最好的 玩 | 可能性 | 返回 打 | 返回 站立 |
| 2010年1月5日 | -0.540978 | -0.539872 | 站立 | 0.132024 | -0.071422 | -0.071276 |
| 1/6/9 | -0.536558 | -0.540151 | 打 | 0.059837 | -0.032106 | -0.032321 |
| 1/7/8 | -0.537115 | -0.537003 | 站立 | 0.059837 | -0.032139 | -0.032133 |
| 2010年2月4日 | -0.540947 | -0.541 | 打 | 0.237478 | -0.128463 | -0.128475 |
| 2/5/9 | -0.542105 | -0.540534 | 站立 | 0.039891 | -0.021625 | -0.021563 |
| 2/6/8 | -0.537701 | -0.540773 | 打 | 0.059837 | -0.032174 | -0.032358 |
| 2/7/7 | -0.538271 | -0.537584 | 站立 | 0.028983 | -0.015601 | -0.015581 |
| 2010年3月3日 | -0.540385 | -0.540995 | 打 | 0.115028 | -0.06216 | -0.06223 |
| 3/4/9 | -0.541769 | -0.540536 | 站立 | 0.059837 | -0.032418 | -0.032344 |
| 3/5/8 | -0.54295 | -0.540022 | 站立 | 0.039891 | -0.021659 | -0.021542 |
| 3/6/7 | -0.538575 | -0.540228 | 打 | 0.059837 | -0.032227 | -0.032326 |
| 4/4/8 | -0.543188 | -0.54003 | 站立 | 0.028983 | -0.015743 | -0.015652 |
| 4/5/7 | -0.544396 | -0.539483 | 站立 | 0.039891 | -0.021717 | -0.021521 |
| 4/6/6 | -0.539446 | -0.542878 | 打 | 0.028983 | -0.015635 | -0.015735 |
| 5/5/6 | -0.545033 | -0.542137 | 站立 | 0.009661 | -0.005266 | -0.005238 |
| 全部的 | 1 | -0.540355 | -0.540293 |
底行右側的兩個數字表明,要牌的總體預期值為 -0.540355,停牌的總體預期值為 -0.540293。因此,停牌是略微更好的打法。遵循這條規則,每 1117910 手牌就能額外獲得一個單位。這項建議需要玩家每週玩 40 小時的二十一點,大約需要 5 年才能讓他節省一個單位。
我喜歡用你的二十一點附錄3來調整我的線上單副牌二十一點玩法。我看到你在12月更新了這個頁面,似乎在雙張牌部分有一些新的玩法。我不明白為什麼建議用10和2對抗4,尤其是在莊家爆牌可能性很大的6的情況下。而且,真的可以只打這些牌,而不打中5,就一定正確嗎? !我很感激你能提供任何見解。關鍵在於莊家可以同時持有6和A嗎?嗯,這很有道理。這些是新策略嗎?如果是,是什麼促使它們產生的?
是的,我對兩張牌的牌型清單做了一些修改。我刪除了“9+3 對 3”,並添加了“10+2 對 6”。在單副牌遊戲中,如果莊家拿到軟 17 點停牌,而玩家拿到 10+2 點,莊家拿到 6 點,那麼拿牌的預期值為 -0.159436,而停牌的預期值為 -0.160379。因此,拿牌的平均損失較小。我不想對基本策略給出簡潔扼要的答案,因為牌的出牌方式多種多樣。莊家拿到 6 點爆牌的機率比較大。然而,正如你所說,莊家拿到 6 點時更有可能拿到 17 點,而不是 5 點。 17 點不是好牌,會促使玩家拿牌並試圖擊敗它。
如果你有15點,而莊家亮出8點…基本策略是要牌。在這種情況下,無論你要牌還是停牌,你輸的機率都超過70%……既然無論你要牌還是停牌,你的輸機率都超過70%,為什麼投降不是更好的選擇呢?
為了簡單起見,我們繼續使用你的例子,假設你擊中了,獲勝的機率是70%,失敗的機率是30%。擊中的預期值為0.3*1 + 0.7*-1 = -0.4。這大於投降的預期值-0.5。
我只是想確認一下,在Microgaming的單副牌遊戲中,A,A vs A的正確玩法是按照你的基本策略卡上顯示的分牌。我非常確定正確的玩法應該是拿牌,至少在四副牌的情況下是這樣。而且看起來,如果所有10都還剩下,你很可能經常會輸掉兩倍的賭注。我不是不相信你,只是想確認一下。你有沒有想過,這手牌拿牌和分牌的期望值是多少?
我曾多次被問及這個問題,並始終堅持認為,儘管輸掉了全部賭注,但抽牌分牌A的選擇克服了歐洲的「不偷看」規則,因此分牌是更好的玩法。基於一副牌,每手牌的預期價值(考慮到莊家拿到黑傑克的可能性)為:要牌-0.532849,分牌-0.223277。因此,分牌比四副牌更好,大約31%的單位。對於四副牌的遊戲來說,分牌也是更好的選擇,Microgaming 的玩家不應該玩四副牌遊戲,因為有相同規則的單副牌遊戲可供選擇。
在對二十一點進行無限套牌分析之後,我偶然發現了您的網站,分析規則和您的一樣(莊家所有17點停牌,除了Ace只能分牌一次外,其他四手牌都可以重新分牌,分牌後加倍,分牌Ace時只抽一張牌)。在比較預期值時,我得到的結果和您一樣,除了對子分牌略有不同。所以我想知道您是如何計算分牌預期值的?
我花了好幾年才自己弄好分牌對子。 Gambling Tools的 Cindy 給了我很大的幫助。 Peter Griffin 在《二十一點理論》第 11 章中也談到了這個主題。假設我想計算莊家 2 點時分牌 8 的期望值。最多可以重新分牌 4 手。以下是我的做法。
- 從鞋子裡取出一張 2 和兩張 8。
- 決定玩家不會在任何一手牌中拿到第三個八的機率。
- 遍歷除 8 之外的所有點數,從牌堆中減去該點數,用該點數和 8 打出一手牌,確定期望值,然後乘以 2。假設另一個 8 的機率為零,則確定每個點數對應的機率。將每個點數對應的機率與期望值進行點積。
- 將此點積乘以步驟 2 中的機率。
- 決定玩家重新分牌為 3 手的機率。
- 從牌堆中再取出 8。
- 重複步驟 3,但乘以 3 而不是 2。
- 將步驟 7 的點積乘以步驟 5 的機率。
- 決定玩家重新分牌為 4 手的機率。
- 從鞋子裡取出另外兩個 8。
- 重複步驟 3,但乘以 4 而不是 2,這次考慮獲得 8 作為第三張牌,對應於玩家被迫停止重新分牌的情況。
- 將步驟 11 的點積乘以步驟 9 的機率。
- 新增步驟 4、8 和 12 中的值。
最難的部分是第三步。我有一個非常難看的子程序,裡面全是我用機率樹計算的長公式。當莊家拿到10或A時,它就變得特別難看了。
我有個關於你的八副牌二十一點策略的疑問。首先,這個問題背後的基本假設是,拿到軟17點對莊家有利。為什麼這個策略要求玩家在莊家可能拿到軟17點(例如,莊家亮出A或6)的情況下更頻繁地加倍,而在莊家拿到軟17點停牌的情況下卻不加倍?如果拿到軟17點能讓莊家更有優勢,為什麼玩家會在這種時候投入更多資金呢?這兩張圖表可能互換了嗎?
你說得對,一般來說,拿到軟17點對莊家有利。但這只是一個普遍現象,並非適用於所有情況。當你手牌強到18到21點時,你希望莊家在軟17點停牌。然而,如果你手牌弱到17點以下,你希望莊家拿到軟17點。舉個策略差異的例子:當莊家拿到軟17點時,你應該用軟19點對6加倍;如果莊家拿到軟17點停牌,你應該停牌。這是因為加倍很可能會抽到壞牌,導致點數達到16點或更低。當莊家拿到軟17點時,他爆牌的次數更多,所以在這個例子中,加倍會更安全一些。
您已經向我展示瞭如何在玩擲骰子時獲利。謝謝!現在您的網站正在教我玩二十一點。我有個問題:比如說,當你拿到兩張5,想要加倍下注時,你會在原先的賭注旁邊再加註。那麼,荷官怎麼知道你不是想分牌呢?謝謝!您的網站太棒了!
謝謝你的讚美。要回答你的問題,荷官會直接問你想做什麼。通常情況下,二十一點的所有決定都必須清晰可見,但這是我能想到的唯一例外。不過,如果你想避免輪到你時被問到,只要舉起食指表示你想要一張牌。大多數荷官都知道這意味著什麼。巧合的是,我昨天才知道,在保加利亞,如果你想加倍,就把額外的賭注放在原賭注後面;如果你想分牌,就把額外的賭注放在原賭注旁邊。
另一位讀者寫信說,在北達科他州,州法律規定要遵循保加利亞規則來處理加倍和分割。
你的二十一點基本策略表上寫著,如果莊家的牌是3-6,A、7點牌「如果允許就加倍,否則停牌」。我的問題是,為什麼要停牌?如果你願意加倍卻不能,那至少應該在可以的情況下拿牌吧?反正你也願意再拿一張牌。謝謝你抽出時間!
如果玩家可以選擇加倍下注並停牌,那會比傳統的加倍更好。因此,在這種情況下,拿牌實際上對玩家的牌不利,但為了贏得雙倍的籌碼,這樣做是值得的。
二十一點的基本策略圖規定,如果莊家有一張A,那麼在16點就應該加牌。我想知道,這個策略圖是否考慮到了這樣一個事實:一旦知道保險不賠付,莊家就不會再有10點的牌了?這顯然降低了莊家拿到好牌的幾率,但玩家拿到16點就該停牌嗎?
是的,基本策略假設莊家沒有10。即使在莊家不看牌的歐洲,要牌/停牌策略也是一樣的,因為如果莊家有黑傑克,玩家就毫無希望了。假設莊家有一張A,而沒有黑傑克,那麼在軟17點停牌時,莊家拿到17點或以上的機率是83.3%。所以停牌甚至不是一個很危險的玩法,要牌的機率絕對更大。
如果莊家沒有在牌面顯示 10 的情況下檢查是否有黑傑克,而是在牌局結束時只拿走原始賭注,這是否需要改變策略?
不。只要你只輸掉原始賭注,就應該假設莊家沒有黑傑克。如果莊家真的有黑傑克,你也無能為力。
你提出了數學上的論證,證明玩家應該拒絕保險。然而,你的心理學論證站不住腳。大多數人會覺得,為了爭取1.5個「林中鳥」而放棄手中的一隻鳥,就像個傻瓜。
哦,賭博就是要冒險。成功的賭徒不會試圖最大化每手牌的淨贏機率,而是會冒險最大化他的總回報。無論是在賭博還是在生活中,有時為了長期利益,都必須承擔短期風險。所以,少考慮現在,多考慮未來。
為什麼您的 Blackjack Switch 基本策略表說總是在 12 點時要拿牌?
在二十一點轉換遊戲中,玩家應該更積極地要牌,因為莊家點數為22點會導致平手。在常規二十一點遊戲中,停牌的價值很大程度上體現在莊家爆牌時。而在二十一點轉換遊戲中,許多莊家的贏牌都會轉化為平局,相較之下,要牌是更好的選擇。
我老婆懂二十一點的基本策略,但她堅持要靠直覺打牌。請問哪些牌型最接近50-50,這樣我老婆就能把直覺打法限制在這些牌型上?
我確信這個問題已經有人回答過了,但這是個好問題,所以我再回答一次。以下是一些邊緣玩法,以算牌指數為零為基礎。此列表適用於多副牌的情況,其中莊家在軟17點停牌,允許分牌後加倍。最佳玩法列在最前面,其他玩法列在後面。
- 9 對 2(擊中/加倍)
- 12 對 4(停牌/要牌)
- 12 對 6(停牌/要牌)
- 16 對 10(要牌/停牌)
- 軟 13 對 5(加倍/擊中)
- 軟 15 對 4(加倍/擊中)
- 3、3 對 2(分牌/要牌)
我翻遍了你們的二十一點板塊,就是沒找到「怎麼」投降。我知道投降是怎麼回事,但我是不是只拿一半籌碼就完事了?
不,下注後直到牌局結束都不能動你的籌碼。投降的訊號是用食指在二十一點牌桌上,從左到右,在你的籌碼後面假裝畫一條線。我之前甚至不知道這一點,直到最近一位歐洲朋友在牌桌上做了這個動作。直接說「投降」也一樣有效。
為什麼說在Blackjack Switch遊戲中,當數字為 10 或 11 時,面對數字 9 時不要加倍下注?
原因是,如果莊家拿到22點,而你的牌是21點或更少,那就推牌。這非常有利於莊家,應該會抑制你透過加倍或分牌來增加籌碼。
前幾天我聽說,如果你玩的是6:5的牌局(或者裡約的等額賠付牌局),拿到天生牌時應該加倍下注,以抵消較低的賠付。是這樣嗎?這種玩法的預期損失是多少?
這會是一個糟糕的玩法。例如,如果你在黑傑克上對著5點(六副牌莊家在軟17點停牌)加倍,根據我的黑傑克附錄9I ,你的預期收益將是0.622362。所以,即使在等額投注遊戲中,這仍然是一個錯誤,損失了大約38%的賭注。
Wong在《專業二十一點》第23頁寫道:“如果你以10-2或2-10(其中10表示任何10點牌)的點數拿到12點,並且使用兩副或更少的牌(或者如果莊家在軟17點停牌,則使用七副或更少的牌),你應該要牌。” 對嗎?我理解在一副或兩副牌的遊戲中,依賴牌型的策略有一定的價值,但他說的是,當使用七副牌(S17)時,你應該要牌10-2/2-10!這聽起來不對。
Wong 指的是玩家 12 對抗莊家 4,並引用了 Peter Griffin 所寫的《二十一點理論》第 176 頁。是的,他是對的。在七副牌的遊戲中,要牌的預期值為 -0.210820,停牌的預期值為 -0.211106,因此要牌較高。但是,八副牌的遊戲中,要牌為 -0.2111161,停牌為 -0.211100,因此停牌更高。這是一種非常不確定的玩法,七副牌和八副牌之間確實存在牌數差異。這裡有一個更好的例子。用 A-4 對抗 4,你應該一直加倍直到有 26 副牌,但用 27 副或更多牌來要牌。
當現金回饋適用於總投注金額時(從而給玩家額外的加倍或分牌動力),在互聯網上加倍或分牌有什麼基本策略例外嗎?請假設現金回饋率為0.1%。
我找不到任何一手牌,額外的0.1%的籌碼量會導致策略改變。我能找到的最接近的例子是,基於六副牌,莊家在軟17點停牌,A,4對4。在這手牌中,加倍會讓玩家的預期價值損失略低於要牌的0.3%。所以,如果你能拿到0.3%或更多的籌碼量,那就加倍這手牌。我研究過的其他邊緣牌型,玩家加倍或分牌至少要損失1%,而且我從未見過二十一點中返現如此之高。
在二十一點中,16 對 10 的策略是 R,S,因為一旦您淘汰了 2 張牌,則對於任何數量的牌組,策略都是停牌(不拿牌)。
確實,一般來說,如果玩家有三張或更多張牌,16 點對 10 點時應該停牌。所以,如果我的圖表是基於賭場提供投降選項的,那麼你是正確的。然而,這個假設並非如此。如果我將規則改為 Rs(如果允許投降則投降,否則停牌),那就意味著如果不允許投降,玩家應該在兩張牌 16 點對 10 點時停牌。
在您的二十一點附錄9中,您指出玩家面對10點時,有正期望值擊中10點?例如,假設玩家有六副牌,而玩家的10點由6和4組成,您指出玩家優勢為0.026796 。難道玩家和莊家都要到17點才能拿牌嗎?這應該會給莊家帶來優勢,因為如果雙方都爆牌,莊家就會贏。
原因是玩家的下一張牌可能是A,但莊家的下一張牌不是。我在附錄的解釋中已經提到,我已經假設莊家沒有黑傑克。這就是為什麼在莊家偷看並確認自己沒有黑傑克後,玩家在這種情況下略佔優勢。
在大多數二十一點計數系統中,16對10的索引號是零。所以,如果牌堆完全是中性的,你應該停牌,因為如果點數等於或超過索引號,你就停牌。然而,基本策略表告訴我們要牌。這似乎自相矛盾。
說實話,這是一個老問題了,但我從 Chris F. 那裡得到了更好的答案。他正確地指出,原因在於,在創建基本策略圖表時,他們假設玩家的前兩張牌和莊家的明牌已經從牌堆中移除。一個很好的例子是,在單副牌中,正確的玩法是,當牌堆中有 7,7 時,對 10 停牌,因為牌堆中一半的 7 已經消失了,而這正是你用 3 張牌擊敗莊家 20 所需要的。
在16對10的情況下,玩家的手牌要不是10和6,就是9和7。無論哪種情況,兩張會因為要牌而爆牌的牌都被移除了。因此,牌堆裡有一些不會爆牌的小牌,這給了玩家要牌的動力。雖然這是事實,但我還是持懷疑態度,因為在無限牌堆遊戲中,要牌的機率仍然很高。然而,除了少數網路賭場外,無限牌堆只是一種抽象概念。我很好奇,如果在8副牌的遊戲中,荷官一張牌都沒發,只是說“你有16,我有10,但沒有黑傑克”,那麼最佳玩法是什麼?使用 gamblingtools.net(網站已不存在)上的黑傑克分析器,我輸入了8副牌,然後小心翼翼地把牌堆裡的所有牌都抽光,除了沒有6和2張10。然後我給了莊家一張10,我自己也給了10和6。所以玩家這手牌是用來對抗一副中性牌的,這副牌有31張A-9牌,還有124張10。預期值如下:
10+6 vs 10 — 八副牌
| 玩 | 預期價值 |
|---|---|
| 站立 | -0.5399 |
| 打 | -0.5399 |
雖然預期值數字相同,但小程式會強調停牌是更好的玩法,大概是因為停牌比小數點後四位更高。如果我刪除以下數字:A、2、3、4、5、6、8、10、10、10,以模擬 9、7 對 10,結果也一樣,因為玩家使用的是完全相同的中性牌盒。
這顯示即使在八副牌的遊戲中只有三張牌,移除的效果也有多強大。回到最初的問題,在計算完玩家的兩張牌和莊家的明牌後,零點數反映的是一副完全中性的牌。所以正如我剛才所展示的,進入中性牌堆後,停牌的幾率更大。在無限牌堆中,要牌是正確的,因為沒有移除的效果。如果你在中性牌盒中意外擊中 16 對 10,並拿到一張小牌,那麼莊家就有更大的機會拿到底牌 10。這一事實反映在八副牌遊戲中停牌的預期值更高,但在無限牌堆中無關緊要。以下是無限牌堆遊戲中的預期值:
10+6 vs 10 — 無限牌組
| 玩 | 預期價值 |
|---|---|
| 站立 | -0.5404 |
| 打 | -0.5398 |
在二十一點遊戲中,莊家有時會亮出底牌。在這種情況下,正確的基本策略是什麼?
史丹福‧黃(Stanford Wong)在其著作《基礎二十一點》(Basic Blackjack)中給出了這樣的基本策略,見表46。他也提到,1995年拉斯維加斯波本街賭場(Bourbon Street casino)曾推出一項促銷活動,每50分鐘,荷官會亮出自己的兩張牌,持續五手。據黃稱,在此期間,玩家的優勢約為10%。
拆分後我應該使用您的基本策略例外嗎?
這是個好問題。我個人會根據已經打出的牌,尤其是第二手牌的狀況來判斷邊緣打法。如果非要我這麼做,我會說使用例外策略比只使用基本策略更好。然而,基本策略的例外策略僅適用於第一手牌,因此它們對於分牌來說並不完全準確,因為牌組的組成會略有不同。
我猜你的二十一點策略是針對初始牌(玩家的前兩張牌和莊家的明牌)的基本策略。但是,在拿牌或分牌之後,牌組組成發生了變化,基本策略也可能隨之改變。我認為更合適的是基於二十一點整體遊戲的基本策略,包括分牌和拿牌之後的基本策略。你的初始牌基本策略和整體遊戲的基本策略是否有差異?
是的,我的基本策略圖表旨在根據前兩張牌確定最佳玩法。這是製定基本策略的常用方法。這種方法的一個好處是可以精確計算每種玩法的預期值並與其他來源進行比較。但是,你提出的觀點很有道理。因此,我詢問了《Blackjack Attack》的作者唐·施萊辛格,是否存在任何已知的玩法,其中初始手牌的最佳玩法不同於最大化整個二十一點遊戲的預期值的最佳玩法。他回答說,在雙層牌遊戲中,軟 18 對抗莊家的 A,而莊家在軟 17 點停牌,就是這樣一種玩法。如我的二十一點附錄 9所示,停牌的預期值為 -0.100502,要牌的預期值為 -0.100359。因此,基於前兩張牌,要牌的賠率為 0.000143。但是,看到軟 18 的方式遠不止一張 A 和一張 7。下表顯示了這手牌可能出現的所有方式。
Soft 18 與 Ace 組合分析
| 玩家 牌 | 條件 可能性 | 打 電動車 | 站立 電動車 | 打 返回 | 站立 返回 |
| A7 | 0.621139169 | -0.100359 | -0.100502 | -0.062336906 | -0.062425729 |
| A6A | 0.036728229 | -0.11202 | -0.116009 | -0.004114296 | -0.004260805 |
| A52 | 0.146912917 | -0.111299 | -0.103382 | -0.016351261 | -0.015188151 |
| A43 | 0.146912917 | -0.114804 | -0.103721 | -0.01686619 | -0.015237955 |
| A5AA | 0.001827682 | -0.111395 | -0.105122 | -0.000203595 | -0.00019213 |
| A42A | 0.016814677 | -0.116975 | -0.108233 | -0.001966897 | -0.001819903 |
| A33A | 0.007356421 | -0.132142 | -0.107256 | -0.000972092 | -0.00078902 |
| A322 | 0.020470041 | -0.134229 | -0.11004 | -0.002747673 | -0.002252523 |
| A4AAA | 0.000073486 | -0.117554 | -0.110984 | -0.000008639 | -0.000008156 |
| A32AA | 0.001028802 | -0.134775 | -0.112433 | -0.000138657 | -0.000115671 |
| A222A | 0.000709873 | -0.136788 | -0.114993 | -0.000097102 | -0.00008163 |
| A3AAAA | 0.000002238 | -0.135313 | -0.114821 | -0.000000303 | -0.000000257 |
| A22AAA | 0.000023502 | -0.137312 | -0.117376 | -0.000003227 | -0.000002759 |
| A2AAAAA | 0.000000046 | -0.137859 | -0.119823 | -0.000000006 | -0.000000006 |
| 全部的 | 1 | -0.105806844 | -0.102374694 |
列標題說明
玩家卡:玩家手中的牌
條件機率:假設玩家擁有軟 18 點,而莊家擁有 A 點,則給定手牌組成的機率。
Hit EV:擊中後的期望值
站立EV:站立的預期值
命中回報:機率與命中預期值的乘積
林分回報:機率與林分期望值的乘積
底行右側兩個單元格顯示,總體而言,擊球的預期值為 -0.105807,停球的預期值為 -0.102375。因此,表格顯示停球的賠率為 0.00343。
為了驗證這些結果,我根據相關規則進行了兩次模擬,一次模擬要牌,一次模擬停牌。我只統計了在遊戲過程中出現軟18對抗莊家A的牌局。以下是我的結果。
軟18對Ace模擬
| 軟 17 | 手 播放次數 | 全部的 贏 | 預期的 價值 |
| 站立 | 3857490 | -396224 | -0.102715 |
| 打 | 3208390 | -337572 | -0.105215 |
因此,模擬結果顯示,在所有可能出現這手牌的情況下,停牌的機率為0.0025。因此,從實際玩所有牌的角度考慮,最佳玩法是停牌,這與我的基本策略圖所示相反。
您好。我剛剛偶然發現了您的網站,我覺得這是一個非常棒的二十一點資訊網站。不過我有個問題。您能解釋一下,當您遵循基本策略,並且總牌點數為10,而莊家明牌為10或A(莊家沒有黑傑克)時,為什麼會有正期望值嗎?您的表格顯示了這兩種情況下的正期望值,但我不明白是怎麼回事。我認為在這種情況下,玩家和莊家遵循相同的策略,即要牌直到17點或更高,否則爆牌。在這種情況下,玩家的軟17點會被淘汰,所以我不明白正期望值從何而來。
感謝您的讚美。假設有六副牌(莊家在軟17點時要牌或停牌都無所謂)。我的二十一點附錄9顯示,6+4對A的預期值為+0.081336,6+4對10的預期值為+0.026796。預期值為正的原因是,我的預期值表假設莊家已經偷看過黑傑克,並確認自己沒有。同時,玩家仍然可以抽到一張A,湊成21點。換句話說,玩家可以在下一張牌湊成21點,而莊家不能,這是假設。如果我有一張符合歐洲不偷看規則的預期值表,那麼預期值確實會是負數。
我最近去拉斯維加斯玩的時候,看到兩個獨立的荷官(一個在奧爾良賭場,一個在馬戲團賭場)建議在4-4對6的時候加倍而不是分牌。我是我們這群人裡最擅長「雙倍」的荷官,所以我的朋友開始問我這個問題。我只能說:不,分牌是正確的決定。 (當然,前提是允許分牌後加倍。)請問這兩個選項的可能性是多少,或者您能告訴我嗎?此致
我以前說過,雖然我很尊重莊家,但他們也給了很多糟糕的建議和錯誤訊息。用四對五或六分牌是一種常見的玩法,玩家和莊家都會錯誤地反對分牌。有時你會聽到有人錯誤地說,你永遠不應該分“任何以F開頭的牌”,也就是四、五和人頭牌。對於五和人頭牌來說,這話沒錯,但如果允許分牌後加倍,玩家確實應該用四對五或六分牌。否則,玩家應該要牌,除非在單副牌遊戲中,如果允許加倍,他應該要牌。我的二十一點附錄9顯示,在六副牌遊戲中,莊家拿到軟17,對6的預期值為4和4。
立場:-0.114085
命中:+ 0.113365
雙精度:+ 0.092929
拆分:+0.207228(允許拆分後加倍)
拆分:+ 0.056954(拆分後不允許加倍)
巫師,我一直在瀏覽您的網站,準備去拉斯維加斯玩一趟,因為它是目前最好的賭博網站。您在2001年12月4日的專欄文章中,分析了16點對莊家10點的持牌時機,這讓我很感興趣。身為數學愛好者,我希望能最大化勝算,但同時也明白微薄的收益。和許多玩基本策略的玩家一樣,當我手上有2、3、4或5點時,我總是能拿到16點對莊家10點。我很好奇,自從你注意到這個問題後,你是否調整了你的玩法,以達到「每5年贏一個單位」的目標,還是堅持每次都拿到16點?謝謝你!
謝謝你的讚美。如果我玩的是基本策略(而不是算牌),如果我手上已經有4或5,我通常會停牌。如果是明牌遊戲,有其他玩家,我會環顧牌桌,然後根據自己的判斷來決定。
在二十一點遊戲中,莊家會亮出兩張牌(附錄 16 ),當莊家的點數為 10 或 11 時,一對 8 不會進行分牌;相反,莊家的點數為 10 時,要牌;當莊家的點數為 11 時,要停。這和常規的 BS 不同,常規的 BS 是將 8 與莊家的 10 或 A 分牌。
在常規二十一點遊戲中,玩家確實應該在莊家拿到10或A時分牌。但是,如果莊家不小心翻開兩張牌,總點數為10或11,玩家應該在10時要牌,在11時停牌。這是因為,當莊家拿到10或A時,輪到你時,你就知道莊家沒有黑傑克,因為他會偷看底牌確認。所以你可以更積極地出牌。但是,當莊家的兩張牌都翻開,總點數為10或11時,莊家肯定可以拿到一張A對應10,或者一張10對應11,總點數為21,所以在這種情況下,你應該採取更保守的策略。
在二十一點的「牌移除效果」中,移除小於5或4的6的效果…是這樣嗎? (我以為6是最佳移除點數,或非常接近5,是最佳移除點數)。謝謝
我覺得你把取牌和莊家的明牌搞混了。下表顯示的是玩家僅根據莊家的明牌,在莊家檢查是否有黑傑克之前,根據莊家的明牌獲得的預期值,假設莊家在軟17點和無限牌上停牌。
莊家明牌的預期值
| 明牌 | 預期的 價值 |
| 2 | 9.10% |
| 3 | 12.38% |
| 4 | 15.85% |
| 5 | 19.65% |
| 6 | 23.40% |
| 7 | 14.40% |
| 8 | 5.82% |
| 9 | -4.06% |
| 10 | -17.36% |
| 一個 | -33.78% |
所以,如果可以為莊家選擇一張明牌,那應該選六。六對莊家不利,對玩家也不利。綜合考慮,如果可以從牌盒中取出一張牌,應該選五。
很棒的網站!你的二十一點策略卡是我見過最好的。哪裡有賣的?我現在用的那個沒有投降選項,用這個會有什麼損失嗎?
謝謝。幾乎每家賭場禮品店都會出售基本的策略卡,但不知為何,他們沒有標明何時應該投降。投降的情況並不多,但這些情況經常發生,所以我認為值得記住。在六副牌的遊戲中,如果莊家拿到軟17點停牌,投降機率為0.07%,如果拿到軟17點,投降機率為0.09%。
我和朋友在拉斯維加斯玩牌。我們大吵了一架,爭論的是,在兩副牌的遊戲中,玩家總點數10,莊家點數7,雙倍下注,還是玩家總點數11,莊家點數10,雙倍下注,哪個從統計上看賠率更高。我以為是前者。
我的二十一點附錄9就是為這類問題設計的。假設有6副牌,我的表格顯示,8+2對7的加倍預期值為0.396342。8+3對10的加倍預期值為0.176919。所以你說得對,10對7的加倍是更好的選擇。
根據標準 BJ 規則和完美的基本策略,我預計我的 DOUBLED DOWN 牌會贏、推和輸的百分比是多少?
假設拉斯維加斯大道的規則較為寬鬆(六副牌,莊家在軟17點停牌,分牌後允許加倍,允許後期投降,允許再次分牌A),以下是最初兩張牌加倍時各種可能結果的機率。這不包括分牌後加倍。
我有個朋友,當他第一張牌是6時就開始抱怨,根本沒等看第二張牌和莊家的明牌是什麼。我覺得他應該等等,因為他可能會拿到2、3、4、5等等(也就是一張不錯的第二張牌),或者莊家也可能亮出2到6(這是一張好牌)。你怎麼看?如果第一張牌是6,而他不知道第二張牌或莊家的明牌是什麼,他的贏錢機率會降低多少?還是我的朋友只是個愛抱怨的人?謝謝你抽出時間。
我的二十一點附錄14顯示,如果你的第一張牌是6,你的預期價值就已經約為-21%。例如,如果他下注100美元,那麼賣出這手牌並下注的合理價格大約是79美元。或許你可以利用他的抱怨,提出以低於79美分的合理價格買下他的牌。我建議75美分的出價,這樣既能為你帶來優勢,又不會佔太多便宜。
上週末我玩二十一點的時候遇到過這種情況,莊家明牌是6,但他在收底牌的時候,不小心亮出了3。我右邊的玩家是15,我是11,左邊的玩家是12。我右邊的玩家知道莊家的總牌數是9,所以他要了一張10,爆牌了。我最後加倍下注,拿到2了。左邊的玩家要了一張5,總牌數是17。莊家開牌是9,要了一張10,總牌數是19。莊家告訴我們,即使你看到了小3,也應該像不知道底牌一樣出牌。我想問一下,如果當時有三位玩家都遇到這種情況,你會怎麼做。自從我玩二十一點以來,這種情況還是第一次發生。請指教。謝謝!
我的閃光二十一點莊家策略展示了在莊家意外暴露底牌的情況下該如何應對。然而,大多數玩家,包括我,都沒有記住這一點。在這種情況下,如果莊家的兩張牌總點數不超過九點,你可以使用基本策略,假設莊家的明牌等於他兩張牌的總和。根據這個經驗法則,三位玩家都玩得正確。與莊家的說法相反,玩家完全有權利用從此類莊家錯誤中收集到的任何資訊。我不僅會無視莊家的評論,還會繼續玩,希望他再犯錯。
感謝您創建了這麼棒的網站,提供如此詳盡的資訊。您提到了二十一點中各種查理牌的莊家優勢顯著降低,但我沒有看到任何關於不同玩法的建議。在大型(6副以上)牌盒中,有沒有什麼值得利用的基本策略例外,可以最大化利潤?我猜想,如果莊家爆牌的可能性很小,那麼如果離查理牌只有一張牌,我可能會拿到更多牌,但我希望看到具體的說明。謝謝。
不用客氣。對於那些可能不明白這個問題的讀者,「查理」規則是指玩家只要拿到一定數量的牌(通常是五到七張)且沒有爆牌,就自動獲勝。下表針對三張或三張以上的牌,顯示了當玩家距離這種自動獲勝者只差一兩張牌時的基本策略。
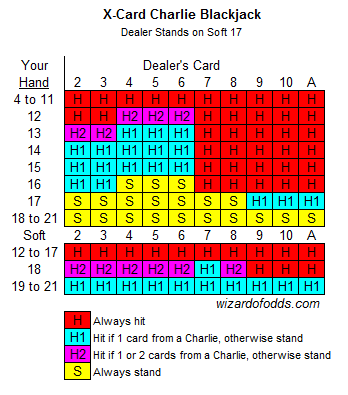
許多賭場允許在二十一點牌桌上,玩家在後方下注。請問,假設兩位玩家聯手下注,當「後方」下注金額遠超過常規下注金額時,正確的分牌策略是什麼?
希望您滿意,我添加了一個新頁面來回答這個問題。請參閱我的“二十一點附錄 19” 。
我研究並使用了你的二十一點附錄16 (莊家揭底牌策略)已經有一段時間了,但仍然有一個玩法我找不到數學解釋:A2 vs. 5。基本策略會將此視為加倍,並且使用你自己的「牌移除效應」數值,當你拿到軟13時,從牌堆中移除2和3應該會讓牌堆對玩家更有利,而不是更不利。我為什麼沒看到?
原因是我的二十一點基本策略是基於8副或更少的牌,而閃牌莊家策略則是基於無限多副牌。在無限副牌的二十一點遊戲中,你也應該打出A2而不是5。無限副牌假設是分析二十一點的偷懶方法。我之所以這樣做,是因為我認為這個頁面不常用,而且錯誤成本非常低,每202,000個單位的賭注只犯一個單位的錯誤。
我覺得我注意到你跟一個21點後下注的玩家分牌策略有個錯誤。它說,如果你的後下注玩家分牌是10對8(這是自私的牌表),你只能玩一手牌。但是,硬10(沒有加倍)對8仍然有正的預期價值。
原因是我的表格假設前排玩家會繼續重新分牌(如果可以的話)。這會降低單張10的價值,因為我假設前排玩家會繼續犯同樣的錯誤(如果可以的話)。我剛剛把這個條件加入了那個頁面。
感謝您提供詳細的網站。在二十一點附錄9中,您列出了遊戲的預期值以及每種玩法的預期值。我預期遊戲的預期值是E i × P i之和,其中E i是第i種玩法(停牌/要牌/加倍/分牌)的最大預期值,P i是第i種玩法的機率。當我嘗試進行此計算時,得到了不同的結果。例如,六副牌,莊家在軟17點要牌,玩家在分牌後不得加倍,我得到的結果是0.04518876。
這些表格假設莊家沒有黑傑克。這是因為輪到玩家行動時,莊家已經偷看了黑傑克。假設莊家沒有黑傑克,正確的加倍或分牌決策應該基於條件期望。否則,玩家面對10或A時,會過於膽怯,不敢加倍或分牌。將機率和期望值的點積相加會得到錯誤的結果,因為莊家拿到黑傑克時,並沒有損失。
要計算整個遊戲的賭場優勢,你應該減去莊家拿到黑傑克時的預期損失。如果是六副牌,莊家拿到黑傑克的機率是10的數量乘以A的數量,再除以兩張牌組合的數量,即 (6×16)×(6×4)/combin(312,2) = 0.047489。然而,玩家只有在沒有黑傑克時才會輸。假設莊家已經有一張黑傑克,玩家拿到黑傑克的機率是 (6×16-1)×(6×4-1)/combin(310,2) = 0.045621。因此,玩家輸給莊家黑傑克的機率是 0.047489 × (1-0.045621) = 0.045323。你應該從上面的點積中減去這個數字:0.04518876 - 0.045323 = -0.00615144。因此,根據附錄中規定的規則,賭場優勢為0.62%。
我 100% 的時間都遵循您的 4+ 副牌二十一點基本策略,每當我拿到 12 點而莊家拿到 2 點,尤其是 3 點時,我總是會遭到鄙視。我不知道如何用簡單的術語向其他玩家解釋為什麼我所做的是最好的事情。
我感同身受。你可以想像西班牙21點有多糟糕,它要求玩家像3點對14點這樣的打法。如果只是表面現象,我就會放過它。如果只是文字問題,我會說:「這裡還有很多其他桌子。」你根本無法用解釋賠率來說服這種傻瓜。信念越荒謬,人們就越容易固執己見。
無論如何,通常沒有簡明扼要的解釋來解釋為什麼一種玩法比另一種玩法更好。要知道為什麼正確的玩法是那樣,你必須要么考慮剩餘牌可能出現的所有情況,無論是玩家還是莊家,要么把這手牌玩上千遍,甚至數百萬遍,直到牌局非常邊緣化。你應該選擇預期價值最高的。只有拒絕保險的玩法才容易解釋。
我知道圖表上是怎麼說的,但在二十一點中,如果莊家有9、10或A,我沒辦法讓自己用8分牌來對抗他。我的問題是,這會對賭場優勢造成什麼影響?
假設有六副牌,莊家在軟17點停牌,玩家可以重新分牌,最多分到四手牌。每次基本策略變化的影響在於該手牌出現的機率以及出現錯誤打法的成本。我的二十一點附錄9顯示了每手牌出現的機率以及每種打法的預期價值。假設玩家選擇要牌而非分牌,對遊戲預期價值的影響如下:
機率(8,8 vs A)×(EV(擊中)-EV(拆分)) + 機率(8,8 vs 9)×(EV(擊中)-EV(拆分)) + 機率(8,8 vs 10)×(EV(擊中)-EV(拆分))
= 0.0003036 × (-0.513551 -(-0.364371)) + 0.0004404 × (-0.505707 -(-0.38995)) + 0.0016249 × (0.53531 -5385)
= -0.019%。
因此,如果莊家拿到 9、10 或 A,而玩家拿到 8、8,賭場優勢就會增加 0.019%,也就是說,每玩 5,300 手牌,賭場優勢就會增加一次。如果玩家選擇投降而不是拿牌,賭場優勢就會降至 0.013%。所以,這並不是一個重大錯誤。相比之下,在六副牌的遊戲中,如果玩家拿到“等額賭注”,而莊家拿到 A,賭場優勢就會增加 0.014%。如果玩家對每張黑傑克和 20 都投保(這是一個常見的錯誤),那麼錯誤成本就會躍升至 0.149%!
這個問題是在我的同伴網站Wizard of Vegas的論壇中提出並討論的。
不久前,我在拉斯維加斯大道上的一家賭場玩6-5的二十一點,當時我喝了不少免費酒,結果每次莊家2-6,我只要拿到二十一點,就加倍下注。幸運的是,我每次都贏了。但是,我不禁懷疑我的決定有多糟糕。如果二十一點的賠率是1比1,那還合理嗎?
我的二十一點附錄9可以解答這類問題。例如,假設有六副牌,莊家拿到軟17,那麼用二十一點對抗莊家5點加倍的預期價值為0.622136,對抗莊家6點加倍的預期價值為0.667063。兩者都遠低於1.2,成本超過一半的賭注。即使二十一點只支付等額的賭注(不幸的是,現在有時確實如此),你也應該在二十一點上停牌。唯一不該在二十一點上停牌的遊戲是三倍21點,玩家在二十一點對抗莊家6點上應該三倍下注。
這個問題是在我的同伴網站Wizard of Vegas的論壇中提出並討論的。
你的二十一點基本策略表是基於最大化每手牌的預期價值。然而,是否存在這樣的情況:加倍或分牌比要牌或停牌略微糟糕,以至於錯誤成本低於額外玩一手牌的賭場優勢?
是的!讓我們考慮以下情況:
6層甲板
莊家拿到軟 17
玩家有 A,6
莊家亮出 2
根據我的二十一點附錄 9 ,以下是每次玩法的預期值:
立場 -0.152739
命中 -0.000274
雙倍 -0.004882
因此,要牌是平均輸錢最少的玩法。若玩家加倍,則誤差的預期值為 -0.004882 - (-0.000274) = -0.004608。根據我的二十一點莊家優勢計算器,在這些規則下(假設投降、分牌後加倍以及A重新分牌),莊家優勢為 0.48%。通常情況下,某些選項是不允許的,從而增加了莊家優勢。因此,只要莊家在六副牌的遊戲中拿到軟 17,那麼在面對 2 時將軟 17 加倍的成本低於在另一手牌上下注相同金額的成本。
在任何涉及加註的遊戲中,你都可以提出同樣的觀點。例如,在三張牌撲克中,如果你想最小化每手牌的預期損失,那麼最佳策略是在Q64或更高牌面加註,正如我在三張牌撲克頁面上所提到的。然而,如果你的目標是最小化每手牌總投注額的預期損失,那麼最佳策略是在Q62或更高牌面加註。
這就引出了一個問題:為什麼像我這樣的賭博作家會以最小化每註初始投注的預期損失而不是總投注金額作為策略基礎?我的答案是,這主要是出於傳統。二十一點基本策略就是這樣誕生的,出於習慣和簡單性,每個人都保留了這個方法。如果休閒玩家的目標是在規定的時間內最小化損失,那麼他應該採用能夠最小化每手牌預期損失的傳統策略。如果玩家的目標是最小化總投注金額超過 x 美元的損失,那麼他應該選擇前面提到的那種略微糟糕的加倍和加註策略。我傾向於認為大多數玩家的目標都是基於時間的,因此更傾向於採用傳統策略。
這個問題是在我的同伴網站Wizard of Vegas的論壇中提出並討論的。
我知道很多二十一點玩家不喜歡在面對9、10或A時用8分牌。你認為這種玩法是最常犯的錯誤嗎?如果不是,你認為是什麼?
我認為二十一點玩家最容易犯錯的玩法是在允許分牌後加倍的情況下,對著5或6分牌,卻用4、4分牌。在六副牌的遊戲中,出現這種情況的機率是1/1135。根據我的二十一點附錄9 ,假設玩家選擇要牌而不是分牌,那麼對著5的預期成本是2.83%,對著6的預期成本是4.38%。總的來說,如果玩家每次都犯這個錯誤,遊戲的莊家優勢就會上升0.0032%。所以,這個錯誤代價不高,因為它很少發生。然而,我從未見過其他玩家在這種情況下正確地分牌。當我看到的時候,荷官和其他玩家通常會翻白眼。有一次,我聽到另一個玩家假裝我不在場,錯誤地對荷官說:“你永遠不應該分任何以F開頭的牌。”
如果問題是,考慮到玩牌頻率和錯誤代價,哪個錯誤代價最大,那麼我只能大膽猜測。我的猜測是,最大的錯誤是沒有在應該軟加倍的時候變得軟加倍。我很少看到業餘玩家用軟17對6這樣的牌加倍。下表顯示了四種常見錯誤所導致的賭場優勢的增加。表格假設玩家在這種情況發生時總是會犯錯,而不是選擇次優選擇。例如,在12對2或3的情況下停牌,我沒有將6、6的玩家納入考慮。
常見的二十一點錯誤
| 錯誤 | 可能性 | 每次事故的平均成本 | 每手成本 |
|---|---|---|---|
| 絕不軟雙 | 0.016430 | 0.054357 | 0.000893 |
| 12 點對 2 點或 3 點停牌 | 0.000380 | 0.029955 | 0.000380 |
| 軟 18 號牌對 9-A 號牌停牌 | 0.000205 | 0.041605 | 0.000205 |
| 擊中 8,8 對抗 9-A | 0.000194 | 0.081779 | 0.000194 |
這個問題是在我的同伴網站Wizard of Vegas的論壇中提出並討論的。
為什麼基本策略說16比10要牌,Hi-Lo點數卻說點數大於或等於零就停牌?基本策略不是基於滿牌,也就是點數為零嗎?看來兩種策略都不可能正確。
首先,值得重申的是,16對10的牌局是一手介於要牌和停牌之間的牌。如果允許投降,那麼對於採用基本策略的玩家來說,這比要牌或停牌要好得多。否則,平均而言,要牌會稍微好一點。只要從八副牌的牌盒中取出一張小牌,就能改變停牌的賠率,因為少了一張小牌,剩下的大牌就更多了,要牌的風險也就更大了。這就是為什麼我說,如果你的16點由三張或更多牌組成,你就應該停牌,因為一張三張16點通常會從牌盒中取出至少兩張小牌。
其次,洗牌後的第一手牌,如果基本策略和算牌策略在如何玩這手牌上有所不同,則以基本策略為準。基本策略是根據觀察到的具體牌型精心設計的,旨在考慮牌堆的具體構成。索引值表是一種更直觀的工具,適用於所有牌盒。
在這種特殊情況下,算牌者可以選擇要牌或停牌,這取決於他如何對真實點數進行捨入。如果他向下舍入,真實點數將為 -1,因此他要牌。如果他向上捨入,即捨入到最接近的整數,則真實點數將為 0,因此他停牌。只要我提到這一點,根據唐·施萊辛格 (Don Schlesinger) 的《黑傑克攻擊》(Blackjack Attack),舍入的首選方法是“向下取整”,即向下舍入,在本例中為 -1,因此玩家可以正確要牌。
另一個類似的情況是 15 對 10。83% 的時間(10+5 或 8+7,但不是 9+6),這會導致洗牌後第一手牌的運行計數為 -1,而投降的索引號為 0。向下舍入會導致玩家錯誤地擊中,而投降是更好的選擇。
重點是,洗牌後第一次做決定時,如果其他玩家沒有其他牌,算牌者應該使用基本策略。之後,恢復使用索引號。
這個問題是在我的同伴網站Wizard of Vegas的論壇中提出並討論的。


