擲雙骰 - 骰子和滾動
我想知道如何改變擲骰子遊戲中的骰子,以便每次擲出 7 或 11,您能幫忙嗎?謝謝。
然後進行修改,使一個骰子的每一面都是六,而另一個骰子的每一面都是一和五。
你認為玩家的「一廂情願」會影響遊戲結果嗎?請注意,我關心的不是影響的大小,而是你的哲學觀點。另外,你認為玩家在玩擲骰子遊戲時擲骰子的方式會導致結果偏差(好壞)嗎?你的網站一如既往地棒極了。
謝謝你的讚美。不,我認為在其他條件相同的情況下,這種一廂情願的想法在賭場裡沒什麼用。
關於骰子影響力的問題一直備受爭議。我個人對此持懷疑態度。當我在2013年回顧這篇回應時,我仍然沒有看到令人信服的證據,表明有人能夠施加足夠的影響力來獲得優勢。
只是想知道您對透過預先設定骰子來改變擲骰子中的頻率表的看法。
我對此非常懷疑。我在我的擲骰子附錄3中回顧了一些關於這個主題的實驗。
我最近學到了一些關於擲骰子遊戲的骰子設定策略。有些人認為,你可以在投擲前以某種方式設定骰子,透過讓骰子只圍繞一個旋轉軸旋轉,在某些骰子組合下,擲出「7」的機率就會降低。我想知道這種說法是否屬實,還是只是一種謬論。
我不相信。到目前為止,我還沒看到任何我尊敬的人支持這種方法,也沒有任何證據表明它有效。雖然我不完全排除這種可能性,但我對此非常懷疑。我雖然住在內華達州,但說到像骰子設定這樣的事情,我來自密蘇裡州,「給我看看」它是否有效。
骰子真的沒有偏見嗎?數字較大且孔洞較多的面似乎比數字較小且孔洞較少的面更輕。這似乎表明,較重的面更有可能面朝下落地,而數字較大的面更有可能面朝上落地。我可以想像一個可以嘗試利用這原理的擲骰子遊戲系統,但我不知道它是否真的有效。你覺得呢?
對於普通骰子,例如你在棋盤遊戲中得到的骰子,確實如此。然而,賭場骰子上鑲嵌著點。他們在工廠裡為這些點鑽孔,然後將白色點嵌入孔中,這些點的密度與骰子本身相同。所以骰子本質上是一個完美的立方體。即使他們使用普通的棋盤遊戲骰子,我也懷疑這種偏差是否足以克服賭場優勢。
您是否相信在賭場擲骰子遊戲中擲骰子的過程與 RNG 一樣是真正隨機的,或者是否存在擲骰子“機制”或純粹的草率投擲(例如短距離投擲)導致擲骰子好與擲骰子差的情況,如果現實世界中的賭場擲骰子遊戲不是真正隨機的,我該如何利用這一點?
我認為不存在天生擲骰子能力差的人。除了少數專業玩家外,所有擲骰子都可以被認為是真正隨機的。有一些研討會教你如何透過進動擲骰子來克服賭場優勢,但我既不贊成也不反對這種做法。我還沒有看到足夠的證據來證明這一點。
在《賭場玩家》雜誌十月刊上,弗蘭克·斯科布萊特寫了一篇關於控制擲骰子的文章,文中你提到斯坦福·黃在500次擲骰子中只擲出74個7,你輸了1800美元。為什麼要押注這麼小的樣本(500次)?一個聲稱能夠控制骰子的人應該願意至少擲5萬次來證明自己的技術。我認為500次擲骰子樣本太小,幾乎任何事情都可能發生,這難道錯了嗎?
我把1800美元輸給了另一位賭博作家,而不是史丹佛。我本來希望擲出更多骰子,但顯然時間有限。假設每分鐘擲一次,擲50000次骰子需要34.7天。 500次不是我決定的,但這似乎是在大樣本量和時間之間做出的合理妥協。你說得對,500次太少了,不足以充分說明影響骰子行為的合理性,但500次總比零次好。
我知道你對骰子控制持懷疑態度。我已經練習了三個月的骰子設定和控制投擲了。隨機投擲655次,擲出78個7的機率是多少?謝謝你的幫忙 :)
對於大量投擲,我們可以使用高斯曲線近似。 655次投擲中,預期出現7的次數為655 × (1/6) = 109.1667。變異數為655 × (1/6) × (5/6) = 90.9722。標準差為sqr(90.9722) = 9.5379。您的78次投擲結果比預期值低109.1667 − 78 = 31.1667。這相當於(31.1667 - 0.5)/9.5379 = 3.22個標準差。低於預期值3.22個或更多標準差的機率為0.000641,即1/1560。我在Excel中使用公式normsdist(-3.22)得出了這個數字。
這是關於擲骰子遊戲的骰子控制。您之前討論過史丹佛黃實驗,其中提到:「賭注的條件是,精準投擲者在500次擲骰子中能否擲出少於79.5個7。在隨機遊戲中,預期數字是83.33。在500次隨機擲骰子中擲出79個或更少7的機率是32.66%…在500個隨機擲骰子中擲出79個或更少7的機率是32.66%…在50014%中擲出14%。
我對這個賭注的疑問是,14.41% 仍然不是「統計上顯著的」 [即 p < 0.05],這通常被認為意味著距離平均值大於兩個標準差 - 或者事件在系列的任一端隨機發生的機率小於*綜合* 5%。
在您可以說結果完全隨機(即結果具有統計意義)的可能性小於 2.5% 之前,需要在 500 次投擲中投出多少個“7”?
非常感謝,順便說一句,您的網站絕對是我發現的有關賭博賠率和概率的最佳網站......繼續努力! ! !
謝謝你的讚美。你不應該說投擲結果非隨機的機率是p。應該這樣表述:一場隨機遊戲產生這種結果的機率是p。沒人指望500次投擲就能證明或反駁任何事情。我並沒有把79.5個7的點數定為79.5,但我懷疑這個點數是否具有統計意義;相反,我懷疑這是一個雙方都會同意下注的點。
2.5% 的顯著水準是與預期值相差 1.96 個標準差。這可以在 Excel 中使用公式 =normsinv(0.025) 計算得出。 500 次投擲的標準差為 sqr(500*(1/6)*(5/6)) = 8.333。因此,1.96 個標準差等於 1.96 * 8.333 = 16.333 次,比預期值低。 500 次投擲中出現七的預期次數為 500*(1/6) = 83.333。因此,比預期值低 1.96 個標準差等於 83.333 − 16.333 = 67。使用二項分佈檢驗,出現 67 次或更少七的準確機率為 2.627%。
三年前,您在“問問巫師”專欄中寫道:“您說得對,500次擲骰子太少,不足以充分論證影響骰子結果的有效性,但500次擲骰子總比零次好。” 您能否描述一下,在實驗中,您需要對所謂的骰子影響者進行哪些操作,才能讓您有足夠的信心開始對他進行大額投注?我之所以問這個問題,是因為在某些二十一點模擬遊戲中,10億輪擲骰子是「可靠」結果的良好基準。在最高效(即需要擲骰子次數最少)的實驗設計下,投擲者需要擲多少次才能確信自己能夠影響結果?我知道答案取決於投擲者的技能,但您明白我的意思。如果即使在最好的情況下也需要擲一百萬次,那麼這項嘗試就不值得了。
信心的建立沒有明確的標準,關鍵在於程度。首先,我會問測試的目的是什麼,以及射手對結果的估計。任何測試都可能出現兩種錯誤。一個熟練的射手可能會因為運氣不好而失敗,或者一個隨機的射手可能會因為運氣好而通過。在這兩種情況下,我更傾向於避免假陽性。我認為合理的測試應該將假陰性的機率設定在5%左右,將假陽性的機率設定在1%左右。
例如,假設索賠人聲稱他平均每擲七次骰子就能擲出一個七。而隨機擲骰子的人平均每擲六次就能擲一個七。透過反覆試驗,我發現,要同時滿足這兩個條件,測試需要擲骰子3600次,並且需要547個或更少的七才能通過,或者每6.58次擲出一個七。
一位七分之一的射手平均應該可以打出514.3個七分,標準差為21.00。使用高斯近似,這位技術嫻熟的射手投出548個或更多七分(假陰性)的機率為5.7%。一位隨機射手平均應該可以打出600個七分,標準差為22.36。一位隨機射手通過測試(假陽性)的機率為0.94%。下圖顯示了技術嫻熟和隨機射手的可能結果。如果結果在綠線左側,那麼我認為該射手通過了測試,我會押注他獲勝。
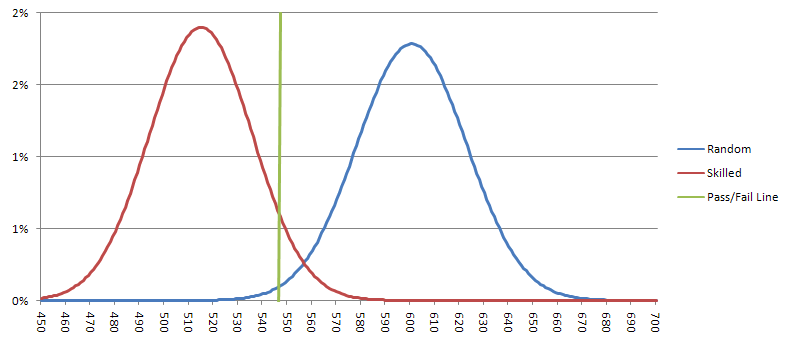
實際的難題是,如果我們假設每分鐘投擲兩次,那麼進行測試將需要30個小時。或許我可以更自由地設定顯著性水平,以減少時間要求,但結果可能不那麼令人信服。我確實認為,現在是時候進行比500次投擲的黃氏實驗更大規模的測試了。
今天的新聞是,大西洋城的一名女子在Borgata 賭場連續擲骰子 154 次才擲出 7 點。這意味著她擲了 154 次骰子,沒有一次 7 點。所以我取 (30/36) 154 ,得到的機率超過 1.5 兆分之一。贏得超級百萬彩票的機率比連續擲 154 次非 7 點骰子馬拉鬆的機率高出約 9,000 倍。考慮到這種情況發生的可能性微乎其微,而且人們被定罪的 DNA 證據中虛假匹配的機率只有數十億分之一,您會懷疑作弊嗎?您會就此事諮詢 Borgata 賭場嗎?我已經打電話給他們,告訴他們我的名字,並告訴他們想怎麼處理就怎麼處理。我很想知道您的想法。
首先,她總共擲了 154 次骰子,第 154 次擲出了 7( 來源:NJ.com )。但是,這並不意味著她在前 153 次擲骰子中從未擲過 7。她可以在 come out 擲骰子時擲出很多 7。正如我在2003 年 5 月 3 日的專欄中指出的那樣,擲到第 154 次的機率是 56 億分之一。贏得超級百萬大獎的機率是 1 / (56,5)*46 = 175,711,536。因此,擲 154 次或更多的難度大約是 32 倍。如果有足夠的時間和表格(我認為是存在的),這樣的事情遲早會發生。所以,我不會懷疑有人作弊。我粗略估計這種情況在任何一年發生的機率約為 1%。
另請參閱我在mathproblems.info上以矩陣表示的解決方案,問題 204。
我認為拉斯維加斯的一些賭場使用的骰子是單面加重的。為了證明這一點,我提交了在拉斯維加斯大道一家賭場收集的244次投擲結果。公平的骰子能產生如此偏差的結果,幾率有多大?
| 骰子測試數據 | |
| 骰子總數 | 觀察 |
| 2 | 6 |
| 3 | 12 |
| 4 | 14 |
| 5 | 18 |
| 6 | 23 |
| 7 | 50 |
| 8 | 三十六 |
| 9 | 三十七 |
| 10 | 二十七 |
| 11 | 14 |
| 12 | 7 |
| 全部的 | 244 |
7.7%。
卡方檢定非常適合這類問題。要使用該檢驗,對每個類別取 (ae) 2 /e,其中 a 是實際結果,e 是預期結果。例如,投擲 244 次,總點數為 2 的預期次數為 244×(1/36) = 6.777778。如果您不明白為什麼投擲 2 的機率是 1/36,請閱讀我的骰子機率基礎知識頁面。總點數為 2 的卡方值,a=6,e=6.777778,因此 (ae) 2 /e = (6-6.777778) 2 /6.777778 = 0.089253802。
卡方結果
| 骰子總數 | 觀察 | 預期的 | 卡方檢定 |
| 2 | 6 | 6.777778 | 0.089253 |
| 3 | 12 | 13.555556 | 0.178506 |
| 4 | 14 | 20.333333 | 1.972678 |
| 5 | 18 | 27.111111 | 3.061931 |
| 6 | 23 | 33.888889 | 3.498725 |
| 7 | 50 | 40.666667 | 2.142077 |
| 8 | 三十六 | 33.888889 | 0.131512 |
| 9 | 三十七 | 27.111111 | 3.607013 |
| 10 | 二十七 | 20.333333 | 2.185792 |
| 11 | 14 | 13.555556 | 0.014572 |
| 12 | 7 | 6.777778 | 0.007286 |
| 全部的 | 244 | 244 | 16.889344 |
然後對卡方列求和。在本例中,和為 16.889344。這稱為卡方統計量。 「自由度」的數量比資料中的類別數少 1,在本例中為 11-1=10。最後,在統計表中找出 10.52 的卡方統計量,自由度為 10,或在 Excel 中使用公式 =chidist(16.889344,10)。這兩種方法都會得到 7.7% 的結果。這意味著公平骰子產生如此或更大偏差結果的機率是 7.7%。總而言之,雖然這些結果的偏差程度比預期的要大,但還沒有嚴重到引起人們的懷疑。如果您繼續進行此測試,我建議收集每個骰子的結果,而不是總和。另外要注意的是,如果某一類別的預期結果數量較低,則卡方檢定並不適用。最低預期值5是常見的數字。
如果擲骰子時兩顆骰子點數相同,會發生什麼狀況?這算有效擲骰嗎?如果有效,荷官會如何透露下方骰子點數是多少?
是否判定為有效擲骰取決於您所在地區。新澤西州博彩法規 19:47-1.9(a) 規定:
當其中一個或兩個骰子離開桌面,或一個骰子停在另一個骰子上面時,擲骰子無效。 ——新澤西州 19:47-1.9(a)
賓州有完全相同的規定, 即第 537.9(a) 條:
當其中一個或兩個骰子離開桌面,或一個骰子停在另一個骰子上面時,擲骰子無效。 ——PA 537.9(a)
我問過一位拉斯維加斯的骰子荷官,他說如果擲骰子的結果在其他方面都正確,那麼這就算有效擲骰。雖然他從未見過這種情況,但他表示,如果真的發生了,荷官會簡單地移動頂部骰子,看看底部骰子落在哪個數字上。然而,人們可以在不觸碰或查看頂部骰子的情況下判斷底部骰子的結果。方法如下。首先,透過觀察骰子的四個面,你可以將前面兩種可能性縮小到兩種。以下是如何根據這三種可能性來判斷。
- 1 或 6:尋找 3。若高點與 5 相鄰,則 1 位於上方。否則,如果高點與 2 相鄰,則 6 位於上方。
- 2 或 5:尋找 3。若高點與 6 相鄰,則 2 位於上方。否則,如果高點與 1 相鄰,則 5 位於上方。
- 3 或 4:尋找 2。如果高點與 6 相鄰,則 3 位於上方。否則,如果高點與 1 相鄰,則 4 位於上方。
這個問題是在我的同伴網站Wizard of Vegas的論壇中提出並討論的。
擲兩顆骰子,如果總數從 2 到 12 至少出現一次,則預期擲兩次骰子的次數是多少?
這個問題是在 TwoPlusTwo.com 上提出的, BruceZ給了正確的答案。以下解答與 BruceZ 的方法相同,值得稱讚。答案比較難,請仔細閱讀。
首先,考慮預期擲出 2 點的次數。擲出 2 點的機率是 1/36,所以平均需要擲 36 次才能擲出第一個 2 點。
接下來,考慮同時擲出 2 和 3 的預期次數。我們已經知道,平均需要擲 36 次才能擲出 2。如果在等待 2 的過程中擲出了 3,那麼就不需要再擲 3 了。然而,如果沒有,就需要擲更多次才能擲出 3。
擲出三的機率是 1/18,所以如果先擲出二,平均需要額外擲 18 次才能擲出三。假設擲出二的方法只有一種,擲出三的方法有兩種,那麼先擲出二的機率是 1/(1+2) = 1/3。
所以,有1/3的機率我們需要額外擲18次才能擲出3。因此,同時擲出2和3的預期次數為36+(1/3)×18 = 42。
接下來,考慮一下你還需要擲多少次才能擲出4。如果你擲出2和3的時候還沒有擲出4,那麼平均下來還需要擲12次才能擲出1次。這是因為擲出4的機率是1/12。
那麼,先得到四,再得到二和三的機率是多少呢?首先,讓我們回顧一下當 A 和 B 不互斥時的一個常見機率規則:
pr(A 或 B) = pr(A) + pr(B) - pr(A 和 B)
你減去 pr(A 和 B),因為這個偶然性在 pr(A) + pr(B) 中被重複計算了。所以,
pr(2 或 3 之前 4) = pr(2 之前 4) + pr(3 之前 4) - pr(2 和 3 之前 4) = (3/4)+(3/5)-(3/6) = 0.85。
在擲出2和3的過程中,沒有擲出4的機率是1.0 - 0.85 = 0.15。因此,需要額外擲12次的機率為15%。因此,擲出2、3和4的預期次數為42 + 0.15*12 = 43.8。
接下來,考慮一下你還需要擲多少次才能擲出5。當你擲出2到4的時候,如果你還沒有擲出5,那麼平均來說,你需要再擲9次才能擲出1,因為擲出5的機率是4/36 = 1/9。
在得到2、3或4之前得到5的機率是多少?一般規則是:
pr (A 或 B 或 C) = pr(A) + pr(B) + pr(C) - pr(A 和 B) - pr(A 和 C) - pr(B 和 C) + pr(A 和 B 和 C)
因此,pr(2 或 3 或 4 之前 5) = pr(2 之前 5)+pr(3 之前 5)+pr(4 之前 5)-pr(2 和 3 之前 5)-pr(2 和 4 之前 5)-pr(3 和 4 之前 5)+pr(2、3 和 4 之前 5) = (4/5)+(4/6)+(4/7)-(4/7)-(4/8)-(4/9)+(4/10) = 83/90。從 2 到 4 的過程中沒有擲出 4 的機率是 1 - 83/90 = 7/90。因此,有 7.78% 的可能性需要額外擲 7.2 次。因此,擲出 2、3、4 和 5 的預期次數是 43.8 + (7/90)*9 = 44.5。
繼續用同樣的邏輯,計算總數從 6 到 12 的機率。每次計算下一個數字作為最後一個數字之前的機率時,所需的計算次數大約翻倍。當總數達到 12 時,你將需要進行 1,023 次計算。
這是 pr(A 或 B 或 C 或 ... 或 Z) 的一般規則
pr(A 或 B 或 C 或 ... 或 Z) =
pr(A) + pr(B) + ... + pr(Z)
- pr (A 和 B) - pr(A 和 C) - ... - pr(Y 和 Z) 減去兩個事件的每種組合的機率
+ pr (A and B and C) + pr(A and B and D) + ... + pr(X and Y and Z) 將三個事件的每種組合的機率相加
- pr (A 和 B 和 C 和 D) - pr(A 和 B 和 C 和 E) - ... - pr(W 和 X 和 Y 和 Z) 減去四個事件的每種組合的機率然後不斷重複,記住奇數事件的機率加起來,偶數事件的機率減去。對於大量可能發生的事件,這顯然會變得繁瑣,實際上需要電子表格或電腦程式。
下表顯示了每一步的預期點數。例如,擲出 2 需要擲 36 點,擲出 2 和 3 需要擲 42 點。右下角單元格顯示擲出全部 11 個點數的預期次數為 61.217385。
預期擲骰次數問題
| 所需最高數量 | 可能性 | 如果需要的話,預期的捲 | 不需要機率 | 所需機率 | 預計總擲骰數 |
|---|---|---|---|---|---|
| 2 | 0.027778 | 36.0 | 0.000000 | 1.000000 | 36.000000 |
| 3 | 0.055556 | 18.0 | 0.666667 | 0.333333 | 42.000000 |
| 4 | 0.083333 | 12.0 | 0.850000 | 0.150000 | 43.800000 |
| 5 | 0.111111 | 9.0 | 0.922222 | 0.077778 | 44.500000 |
| 6 | 0.138889 | 7.2 | 0.956044 | 0.043956 | 44.816484 |
| 7 | 0.166667 | 6.0 | 0.973646 | 0.026354 | 44.974607 |
| 8 | 0.138889 | 7.2 | 0.962994 | 0.037006 | 45.241049 |
| 9 | 0.111111 | 9.0 | 0.944827 | 0.055173 | 45.737607 |
| 10 | 0.083333 | 12.0 | 0.911570 | 0.088430 | 46.798765 |
| 11 | 0.055556 | 18.0 | 0.843824 | 0.156176 | 49.609939 |
| 12 | 0.027778 | 36.0 | 0.677571 | 0.322429 | 61.217385 |
這個問題是在我的同伴網站Wizard of Vegas的論壇中提出並討論的。
據Craps Advantage Players網站稱,拉斯維加斯的賭場經常使用加重骰子來增加七點的機率,從而增加利潤。我簡直不敢相信!巫師對此有何看法?
巫師說那個網站聽起來滿嘴胡言亂語,沒有任何可信的證據來證明指控的合理性。如果我有證據,我很樂意揭露任何賭場使用有偏見的骰子。
如果有人有確鑿的證據證明骰子有偏差,我很樂意進行檢驗並發表我的結論。我希望看到的證據要么是擲骰子的日誌文件,要么最好是一些實際存在的所謂偏差骰子。
此外,如果賭場使用的骰子確實產生了超過預期的「七」的數量,那麼為什麼這些偵探不知道賭「不通過」和下注賠率的陰謀呢?
老虎機上的「Hot Roll」獎勵回合將根據兩枚骰子的總點數獎勵玩家以下數量的硬幣。玩家持續收集硬幣,直到擲出總點數「7」為止,獎勵結束。如果第一次擲出“7”,他將獲得70枚硬幣的安慰獎。除「7」之外,其他所有點數的獎勵如下:
- 2或12:1,000
- 3或11:600
- 4或10:400
- 5或9:300
- 6或8:200
我的問題是平均獎金是多少?
點擊以下按鈕看答案。
答案是 1983.33。點擊以下按鈕以取得解決方案。
[/spoiler] 設答案為 x。只要玩家沒有擲出 7,他就能預期未來的勝率總是 x,加上之前的所有勝率。換句話說,擲骰子具有無記憶特性,即無論你已經擲出多少次,你都不會比開始時更接近 7。我不會深入討論骰子機率的基礎知識,但只是說每個總數的機率如下:
- 2:1/36
- 3:2/36
- 4:3/36
- 5:4/36
- 6:5/36
- 7:6/36
- 8:5/36
- 9:4/36
- 10:3/36
- 11:2/36
- 12:1/36
在考慮安慰獎之前,x 的值可以表示為:
x = (1/36)*(400 + x) + (4/36)*(300 + x) + (5/36)*(200 + x) + (5/36)*(200 x +) (3/36)*(400 + x) + (2/36)*(600 + x) + (1/36)*(1000 + x)接下來,將兩邊乘以 36:
36x = (1000 + x) + 2*(600 + x) + 3*(400 + x) + 4*(300 + x) + 5*(200 + x) + 5*(200 + x) + 4*(300 + x) + 3*(400 + x) + x + 236倍=11,200+30倍
6倍=11,200
x = 11,200/6 = 1866.67。
接下來,安慰獎的價值是700*(6/36)=116.67。
因此,獎金的平均贏額為 1866.67 + 116.67 = 1983.33。
[/spoiler]


