請問巫師 #426
假設一個序號從 1 開始依序編號。流通中的序號最大值未知。給定 n 個隨機抽樣,最大序號的最佳估計值是多少?
我喜歡用計算序號平均間距的方式來解答這個問題。計算方法是用最大值除以樣本容量。例如,如果樣本中最大的序號是 1000,樣本容量為 5,那麼平均間距就是 1000/5=200。然後把這個平均間距加到最大序號上,就能得到估計的最大序號。在這個例子中,1000+200=1200。
通常的計算公式是 M*(k+1)/k,其中 M 為最大值,k 為觀測次數。在本例中,該公式得出 1000*(6/5) = 1200。
如圖所示,ABCD 為邊長為 10 的正方形。在其內部分別內切了一個半圓和一個四分之一圓。
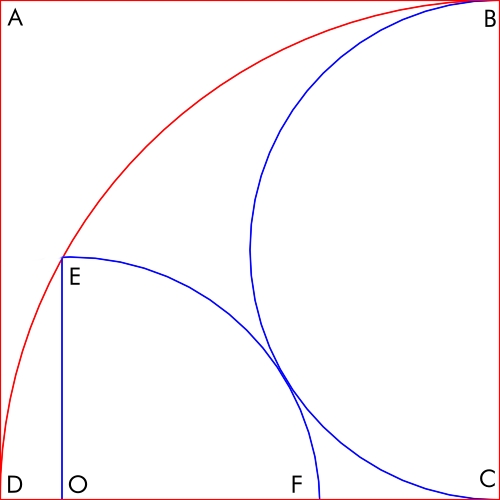
OE的長度是多少?
請參考下圖。
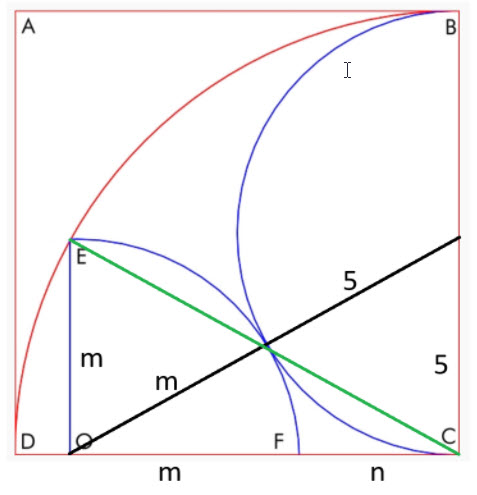
這裡有兩個直角三角形,一個斜邊為綠色,另一個斜邊為黑色。我們來列出這兩個三角形的勾股定理方程式:
- 綠色斜邊: m² + (m+n) ² = 10²
- 黑邊斜邊: 5² + (m+n) ² = (m+5) ²
讓我們將第一個方程式重新整理為 (m+n) 2 = 10 2 - m 2
讓我們把 (m+n) 2的值代入第二個方程式:
5² + 10² - m² = (m+5) ²
25 + 100 - m 2 = m 2 + 10m + 25
2m² + 10m - 100 = 0
m² + 5m - 50 = 0
用勾股定理求解 m:
m = (-5 +/- sqrt(25 + 200))/2
m = 5 或 -10。5 是唯一合理的答案。
[劇透結束]這個問題在我的Wizard of Vegas論壇上被提出和討論。
大量學生參加一個包含 10 題的測驗。每題都是判斷題。最多有多少學生參加測試,才能保證任兩份試卷的題目至少不同兩道?
選取其中一項測試作為我們稱為關鍵測試的測試。
第 1 組 = 其他測驗與關鍵測驗恰好相差 2 題的方法數為 combin(10,2)=45。
我不會計算與關鍵測試結果相差 3 的方法數,因為其中一些方法與第 1 組的測試結果有 9/10 的匹配度。
第二組 = 其他測驗與關鍵測驗恰好相差 4 題的方法數為 combin(10,4)=210。這些測驗中的任何一個都至少與第一組中的任何測驗相差 2 題。
重複這個邏輯…
- 第 3 組 = 其他測驗與關鍵測驗剛好有 6 題不同的方法數為 combin(10,6)=210。
- 第 4 組 = 其他測驗與關鍵測驗恰好相差 8 題的方法數為 combin(10,8)=45。
- 第 5 組 = 其他測驗與關鍵測驗恰好相差 10 題的方法數為 combin(10,10)=1。
所以,答案是第 1 組到第 5 組的總和加上關鍵測驗的 1 = 1+45+210+210+45+1 = 512。
這個數字和 2 的 9 次方一樣。這會是巧合嗎?不!
從一組較大的物品中抽取奇數個物品的方法數與抽取偶數個物品的方法數相同。這是因為大組中的每個物品都可以被選中或不被選中。對於包含 n 個物品的群組,每個物品被選中或不被選中共有 2^n 種組合。如果以二進位順序系統性地列出這些組合,則奇數和偶數的組合數會交替出現。由於該組的總數為 2^n,而 2^n 本身是偶數,因此 2^n 的一半是偶數。
因此,第 1 組到第 5 組題目的數量總和,就是選擇偶數個與關鍵測驗題相符的題目的方法數。這等於是選擇奇數個與關鍵測驗題相符的題目的方法數。與關鍵測驗題符相符或不符的總方法數為 2^10 = 1024。其中一半的題目匹配偶數次。所以,答案是 1024/2 = 512。
這個問題在我的Wizard of Vegas論壇上被提出和討論。


