請問巫師 #321
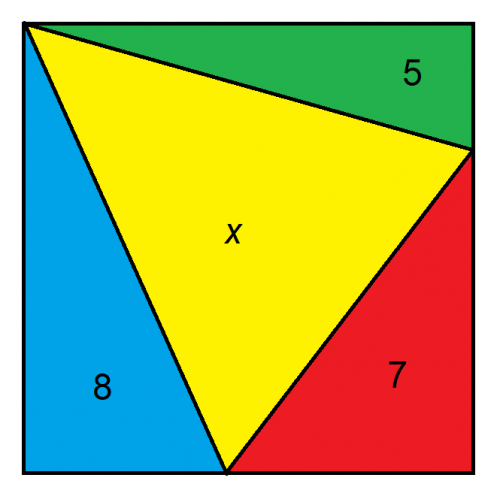
假設較大的圖形是正方形,x 的面積是多少?
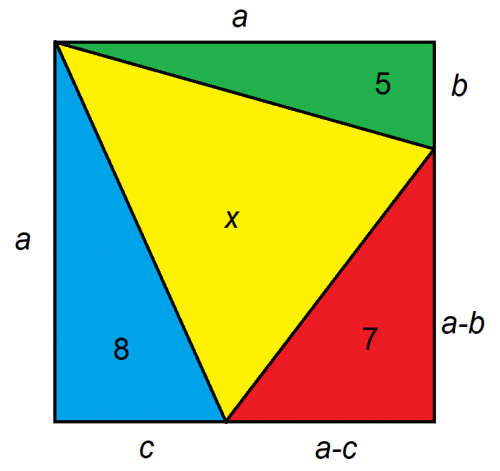
解決這類問題的關鍵在於如何設定它們。我建議盡量將問題簡化為盡可能少的未知數。在本例中,我們可以將正方形上的未知距離表示為三個,如下所示:
處理矩形比處理三角形更容易。已知三個三角形的面積,我們可以將長方形的大小和麵積都加倍。這樣一來:
- ab=10
- ac=16
- (ab)(ac)=14
讓我們分解 (ab)(ac):
a 2 - ab - ac + bc = 14
2-10-16 + bc = 14
(1) a2 +bc=40
讓我們用 a 來表示 b 和 c,以將其歸結為單一變數:
b = 10/a
c = 16/a
用這些值代替方程式 (1) 中的 b 和 c:
2 + (10/a)*(16/a) = 40
a2 + 160/ a2 = 18
接下來,讓我們將所有數字乘以2來去掉分母中的2 。
4 + 160 = 40 * 2
4-40 * 2 +160=0
讓我們定義一個新變數 y = a 2
y 2 - 18y + 32 = 0
接下來,讓我們使用二次公式來解 y:
y = (40 +/- 平方根(1600-640))/2
y = (40 +/- 平方根(960))/2
y = (40 +/- 8*sqrt(15))/2
y = 20 +/- 4 * sqrt(15)
整個正方形的面積是2 ,剛好等於 y。根據上面的公式,如果 +/- 為負,則 y = apx 4.5081,這顯然是錯誤的,因為我們知道面積至少是 20,甚至不包括 x。因此,正方形的面積必須是 20 + 4*sqrt(15)。
給定三個三角形,其面積分別為 5+7+8=20。以正方形的總面積減去該面積,可得 x 的面積:20 + 4*sqrt(15) - 20 = 4*sqrt(15) = apx 15.4919。
這個問題是在我的「拉斯維加斯巫師」論壇中提出並討論的。

注意照片裡我的T卹。我去看《原鑽》的時候,電影院收銀員誇我穿了這件T卹。為了報答她,我用這題折磨她,只用面積分別為2、3和4的三角形。電影結束後,我去看她,她還是沒解出來,但似乎在努力。於是,我在陽光海岸酒吧給她寫了下面的解法。她似乎很欣賞。我覺得這位年輕女士的人生一定會很成功。
關於彩票,在跨州彩票(強力球、超級百萬)中,是否存在一個“臨界點”,即大獎被分割的可能性大於最終只有一個中獎者的可能性?如果存在,這個「臨界點」是多少?
我不會深入討論所有的數學問題,但以下是多個獲勝者與只有一個獲勝者的可能性相同的累積獎金點:
- 強力球:9.75億美元
- 超級百萬:16.5億美元
並不是您問的,但這裡列出的是至少有一個獲勝者的機率等於沒有獲勝者的機率(50%)。
- 強力球:7.04億美元
- 超級百萬:8.67億美元
這個問題是在我的「拉斯維加斯巫師」論壇中討論過的。
- 監獄裡有12名囚犯,每人編號為1到12。
- 監獄長設置了12個箱子,每個箱子編號為1到12。
- 12 個盒子裡面是數字 1 到 12,隨機放置,每個盒子一個。
- 每位囚犯每次可自行選擇開啟六個箱子。囚犯每次可選擇一個開啟。
- 每個囚犯的目標是在六個選擇框中找到自己的號碼。如果找到了,則該人存活。
- 如果一名囚犯找不到自己的號碼,那麼整個團隊就被認為失敗了,他們會立即被帶到行刑隊。
- 如果一名囚犯倖存下來,那麼他必須將數字放回原來的盒子中,以便下一個囚犯使用。
- 遊戲開始後,囚犯不得觀看其他玩家或進行交流。
- 在開始之前,全組成員需要共同製定一個策略。目標是12名囚犯全部存活下來(也就是在盒子裡找到自己的號碼)。
他們的策略應該是什麼來最大限度地提高生存機率,這個機率是多少?
[劇透=解]
就像「秘密聖誕老人」遊戲一樣,遊戲中會有從一個數字到另一個數字的循環。如果有12名囚犯,循環的數量可以是1到12個。如果沒有循環大於6,那麼每個囚犯最終都會找到自己的數字。最大的問題是,沒有循環大於6的機率是多少?讓我們反過來算一下,找出循環大小為7或更大的組合數。
12囚徒解決方案
| 循環 | 組合 | 可能性 |
|---|---|---|
| 12 | 39,916,800 | 0.083333 |
| 11,1 | 43,545,600 | 0.090909 |
| 10,2 | 23,950,080 | 0.050000 |
| 10,1,1 | 23,950,080 | 0.050000 |
| 9,3 | 17,740,800 | 0.037037 |
| 9,2,1 | 26,611,200 | 0.055556 |
| 9,1,1,1 | 8,870,400 | 0.018519 |
| 8,4 | 14,968,800 | 0.031250 |
| 8,3,1 | 19,958,400 | 0.041667 |
| 8,2,2 | 7,484,400 | 0.015625 |
| 8,2,1,1 | 14,968,800 | 0.031250 |
| 8,1,1,1,1 | 2,494,800 | 0.005208 |
| 7.5 | 13,685,760 | 0.028571 |
| 7,4,1 | 17,107,200 | 0.035714 |
| 7,3,2 | 11,404,800 | 0.023810 |
| 7,3,1,1 | 11,404,800 | 0.023810 |
| 7,2,2,1 | 8,553,600 | 0.017857 |
| 7,2,1,1,1 | 5,702,400 | 0.011905 |
| 7,1,1,1,1,1 | 570,240 | 0.001190 |
| 全部的 | 312,888,960 | 0.653211 |
下表顯示了上表中組合的公式。
組合配方
| 循環 | 組合 | 公式 |
|---|---|---|
| 12 | 39916800 | =事實(11) |
| 11,1 | 43545600 | =組合(12,11)*事實(10) |
| 10,2 | 23950080 | =組合(12,10)*事實(9) |
| 10,1,1 | 23950080 | =組合(12,10)*事實(9) |
| 9,3 | 17740800 | =組合(12,9)*事實(8)*事實(2) |
| 9,2,1 | 26611200 | =組合(12,9)*組合(3,2)*事實(8) |
| 9,1,1,1 | 8870400 | =組合(12,9)*事實(8) |
| 8,4 | 14968800 | =組合(12,8)*事實(7)*事實(3) |
| 8,3,1 | 19958400 | =組合(12,8)*組合(4,3)*事實(7)*事實(2) |
| 8,2,2 | 7484400 | =組合(12,8)*組合(4,2)*事實(7)/2 |
| 8,2,1,1 | 14968800 | =組合(12,8)*組合(4,2)*事實(7) |
| 8,1,1,1,1 | 2494800 | =組合(12,8)*事實(7) |
| 7.5 | 13685760 | =組合(12,7)*事實(6)*事實(4) |
| 7,4,1 | 17107200 | =組合(12,7)*5*事實(6)*事實(3) |
| 7,3,2 | 11404800 | =組合(12,7)*組合(5,3)*事實(6)*事實(2) |
| 7,3,1,1 | 11404800 | =組合(12,7)*組合(5,3)*事實(6)*事實(2) |
| 7,2,2,1 | 8553600 | =組合(12,7)*組合(5,2)*組合(3,2)*事實(6)/2 |
| 7,2,1,1,1 | 5702400 | =組合(12,7)*組合(5,2)*事實(6) |
| 7,1,1,1,1,1 | 570240 | =組合(12,7)*事實(6) |
從第一個表格的右下角單元格開始,共有 312,888,960 種輸的組合。這些數字的排列方式總數為 12! = 479,001,600。因此,失敗的機率為 312,888,960 / 479,001,600 = 65.32%。因此,成功的機率為 100% - 65.32% = 34.68%。
[/spoiler]這個問題是在我的「拉斯維加斯巫師」論壇中提出並討論的。
您好。我有一張優惠券,可以讓我把22點的牌推下去。我可以保留這張優惠券直到我拿到第一個22點。這張優惠券不適用於加倍或分牌。這張優惠券的價值是多少?
答案很簡單,就是你允許下注的最高金額。等到22點,再玩,最後就能帶著一個額外的單位離開賭桌。
更嚴格的答案應該考慮等待這 22 的成本。這是我並不確切知道的,但可以估計。
莊家「全壓22」規則對玩家的成本為6.91%。然而,莊家拿到22點的機率會更高,因為玩家不在乎自己是否先爆牌。根據規則,玩家爆牌的機率約為15.7%。如果我們假設這與莊家爆牌的機率無關(事實並非如此),那麼莊家爆牌的機率為6.91%/(1.0-0.157) = 8.2%。
我知道這有點粗略,但我們假設玩家拿到22點的機率相同。我知道莊家爆牌的機率比玩家高,但分牌後這張優惠券也不算數,所以我們就假設這些因素互相抵消了。所以,如果玩家拿到22點的機率是8.2%,那麼他平均每1/0.082 = 12.2手牌就會拿到一次22點。
假設基礎遊戲中的賭場優勢為0.75%。以此賭場優勢玩12.2手牌的成本為12.2*0.0075 = 0.0915。因此,用一個單位的價值減去這個成本,你得到的票面價值為1.0 - 0.0915,約為票面價值的91%。
這個問題是在我的「拉斯維加斯巫師」論壇中提出並討論的。