請問巫師 #318
假設玩家不知道獎品的價格,那麼在「價格猜猜猜」遊戲中玩競賽遊戲的最佳策略是什麼?
為了讓不熟悉該遊戲的讀者了解一下,這裡有一個該遊戲的影片。
我認為以下策略的平均回合數最低。有很多策略可以與之匹敵,但我認為沒有任何策略能超越它。
若要使用該策略,請將四個價格標籤標記為 1、2、3 和 4。根據您過去正確回答的問題的歷史記錄,從左側的第一個轉彎開始,將它們放在四個獎品上。
競賽遊戲策略
| 歷史 | 一等獎 | 獎品二 | 三等獎 | 獎品 4 |
|---|---|---|---|---|
| 沒有任何 | 1 | 2 | 3 | 4 |
| 0 | 2 | 1 | 4 | 3 |
| 0,0 | 3 | 4 | 2 | 1 |
| 0,0,0 | 4 | 3 | 1 | 2 |
| 0,0,2 | 3 | 4 | 1 | 2 |
| 0,0,2,0 | 4 | 3 | 2 | 1 |
| 0.2 | 2 | 3 | 4 | 1 |
| 0,2,0 | 4 | 1 | 2 | 3 |
| 0,2,1 | 2 | 4 | 1 | 3 |
| 0,2,1,0 | 3 | 1 | 4 | 2 |
| 1 | 1 | 3 | 4 | 2 |
| 1,0 | 2 | 4 | 3 | 1 |
| 1,0,0 | 3 | 1 | 2 | 4 |
| 1,0,0,0 | 4 | 2 | 1 | 3 |
| 1,1 | 1 | 4 | 2 | 3 |
| 1,1,0 | 2 | 3 | 1 | 4 |
| 1,1,0,0 | 3 | 2 | 4 | 1 |
| 1,1,0,0,0 | 4 | 1 | 3 | 2 |
| 2 | 2 | 1 | 3 | 4 |
| 2,0 | 1 | 2 | 4 | 3 |
| 2,1 | 1 | 3 | 2 | 4 |
| 2,1,0 | 4 | 2 | 3 | 1 |
| 2,1,1 | 1 | 4 | 3 | 2 |
| 2,1,1,0 | 3 | 2 | 1 | 4 |
下表顯示了在 24 種可能的排列方式中,四個價格標籤需要 1 到 5 次旋轉的機率。
所需回合數
| 轉彎 | 數位 | 可能性 |
|---|---|---|
| 1 | 1 | 4.17% |
| 2 | 4 | 16.67% |
| 3 | 8 | 33.33% |
| 4 | 9 | 37.50% |
| 5 | 2 | 8.33% |
| 全部的 | 24 | 100.00% |
取點積,該策略下所需的平均轉數為 3.29167。
我在Wizard of Vegas論壇上提出並討論了這個問題。
在2019年9月18日播出的《危險邊緣》節目中,有一個名為「描述賭場遊戲」的環節。其中一個線索是“穿著得體,玩得盡興;銀行家的營業時間;邦德先生,您來摩納哥是為了什麼?”

答案是“百家樂”,並被判定為正確。龐德玩的不是二十一點嗎?
是的,邦德玩的確實是二十一點,而不是百家樂。提醒一下,主要區別如下:
- 莊家輪流在牌桌上輪流發牌。莊家玩家自動獲得莊家*牌。
- 玩家*和莊家都可以自由抽第三張牌,只要雙方都沒有兩張自然牌 8 或 9。
筆記:
像往常一樣,在撰寫有關百家樂或二十一點的文章時,我會將賭注的名稱大寫,以避免與玩遊戲的玩家混淆。
話雖如此,第一個這樣的場景出現在下面的《諾博士》片段中,其中不僅銀行旋轉,玩家在第三張牌中擁有自由意志,而且邦德實際上在視頻的 2:11 點口頭上將遊戲稱為“chemin de fer”:
下一個影片展示了三部不同電影中的三個鐵路場景。
以下是每個場景的起點:
- 2:09 — 雷霆萬鈞
- 4:19 — 女王密使
- 7:30 — 只為你的眼睛
在這三部電影中,我們都看到了玩家在第三張牌決策中採取的策略和自由意志,尤其是在《最高機密》中,討論了賠率。
最後,以下是《黃金眼》中的場景。
這裡我們再次看到了莊家輪次的來回切換以及抽第三張牌的自由選擇。然而,在0:45處,女角色確實把這個遊戲稱為「百家樂」。我認為這是“角色錯誤”。
最後,毫無疑問,龐德在每部電影裡都在玩二十一點。嚴格來說,我認為評審們接受「百家樂」作為正確答案是錯誤的。不過,我並不怪他們。即使以《危險邊緣》的標準,指望普通玩家區分百家樂和二十一點也太過分了。正如他們接受“The Mooch”而不是“Anthony Scaramucci”的答案一樣,這表明評委們正在變得更加寬容。
我在Wizard of Vegas論壇上提出並討論了這個問題。
正如電影《賤女孩》中所問,什麼是:
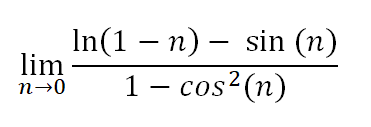
讓我們先查看 n(x 軸)乘以 f(n)(y 軸)的圖表。
如你所見,極限從左邊趨向∞,從右邊趨向-∞。由於極限從兩邊不指向同一個位置,所以不存在極限。
不過,我們先不畫圖來回答這個問題。洛必達規則指出,如果 f(x)/g(x) 的極限 = 0/0,則 lim f(x)/g(x) = lim f'(x)/g'(x)。所以,我們來解 f'(x) 和 g'(x)。
f'(n) = ((ln(1-n) - sin(n)) d/dn = -1/(1-n) - cos(n)
g'(n) = (1 - cos 2 (n)) d/dn = sin 2 (n) d/dn
讓我們用乘積法則來解 sin 2 (n) d/dn
sin 2 (n) d/dn = sin(n) × sin(n) d/dn =
sin(n) × cos(n) + cos(n) × sin(n) =
2sin(n)cos(n)。
接下來,讓我們解 n = 0 時的 f'(n) 和 g'(n)。
f'(0)= -1/(1-0)-cos(0)= -2。
g'(0) = 2sin(0)cos(0) = 0
所以,f'(0)/g'(0) = -2/0 = -∞。因此,原函數的極限並不存在。

我要誇讚《賤女孩》的編劇,他們把數學運用得爐火純青。即使是像《心靈捕手》這樣嚴肅的數學電影,也常常把數學運用得一塌糊塗。