前 n 個整數總和的證明
本週我將證明一個比較簡單的等式:1+2+3+…+n = n(n+1)/2。我會用兩種非常直觀的方式來展示它。這是我目前為止最簡單的證明。不過,在此之前,我先帶給大家我每週的例行邏輯謎題。
邏輯謎題
愛麗絲、鮑伯和科爾發表了以下聲明:
- • 愛麗絲:鮑伯是個騙子。
- •鮑伯:科爾是個騙子。
- • 科爾:愛麗絲和鮑伯都是騙子。
這三個人要不是總是說真話,就是總是說謊。他們都知道另外兩個人是否說真話。那麼,誰在說真話呢?
答案和解決方案請見簡報最後。
前 n 個整數總和的證明
每個人都應該知道,前n個整數和是n(n+1)/2。換句話說,1+2+3+…+n = n(n+1)/2。我將給出兩個簡單的證明來解釋為什麼這是正確的。
方法一
很容易看出,數列的平均數是 (n+1)/2。數列的項數為 n。和等於項數與平均數的乘積 = n × (n+1)/2 = n(n+1)/2。
同樣的方法也適用於求任意起始數和結束數的和。假設起始數為 a,結束數為 b,則平均值為 (a+b)/2,項數為 (a-b+1)。因此,數列中所有數字總和為 (a-b+1) × (a+b)/2。
方法二
下一個方法用圖示比較容易解釋。請看下圖,其中藍色方塊代表整數 1 到 5。
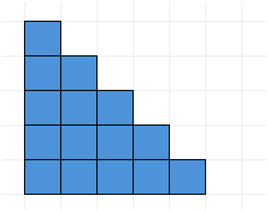
接下來,複製該部分,並將其放置在原件旁邊,如下所示,形成一個矩形。
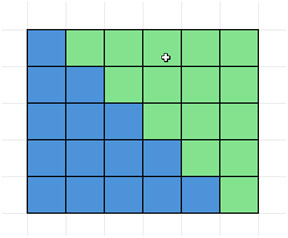
注意上圖矩形的邊長是 5 × 6。一般情況下,如果將 1 到 n 的整數相加,則矩形的邊長是 n × (n+1)。然後,由於我們只要求其中一塊區域的面積,所以需要將該面積除以 2。因此,這塊區域的面積是 n(n+1)/2。
邏輯謎題解答
這三個人都有兩種可能的狀態:說真話或說謊。這樣就有2³ = 8 種可能性。我把所有這些可能性都列在下表中。
| 設想 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| 愛麗絲 | T | T | T | T | F | F | F | F |
| 鮑伯 | T | T | F | F | T | T | F | F |
| 油菜 | T | F | T | F | T | F | T | F |
注意,鮑伯和科爾互相指責對方說謊。這只有在他們之中一人說真話而另一人說謊的情況下才有可能。因此,我們可以排除鮑伯和科爾都說真話的四種情況。剩下的情況是第2、3、6和7種。讓我們逐一分析。
在情境二中,已知愛麗絲說的是真話。她的真話意味著鮑伯是說謊者。然而,鮑伯在這個情景中也是說真話的,這就導致了矛盾。因此,情景二不成立。
在情境3中,已知愛麗絲是誠實的。她說鮑伯是騙子,這在情境3的假設下是正確的。然而,科爾也被列為誠實的人,但他卻說愛麗絲在說謊。愛麗絲不可能同時又誠實又說謊,所以情境3不成立。
在情境7中,已知愛麗絲在說謊。她說鮑伯是個騙子,這沒錯。然而,這樣一來,愛麗絲就成了說真話的人。愛麗絲不可能既說真話又說謊,所以情境7不成立。
這樣就只剩下第六種情況了。我們來驗證一下。如果愛麗絲說謊,那麼鮑伯就是說真話的。如果鮑伯說真話,那麼愛麗絲、鮑伯或他們兩個就都是說真話的。鮑伯說真話,所以科爾的說法是假的。因此,這個假設成立。鮑伯是唯一說真話的人。


