循環調度
本週的主題是如何安排循環賽。首先,我要先解釋循環賽是一種比賽賽制,也就是每位選手與其他選手進行比賽。若比賽有 n 位選手,比賽場次為 n(n-1)/2。
列出 n 位玩家的所有 n(n-1)/2 種可能的配對很容易。然而,理想情況下,每輪遊戲一次,即每位玩家每輪玩一次。以下是如何在玩家人數為偶數的情況下做到這一點。我們以八人的情況為例。在下圖中,我們將玩家標記為 A 到 H,並在四個矩形中顯示兩名玩家的比賽。這四場比賽將構成第一輪。注意每個人的比賽方式。
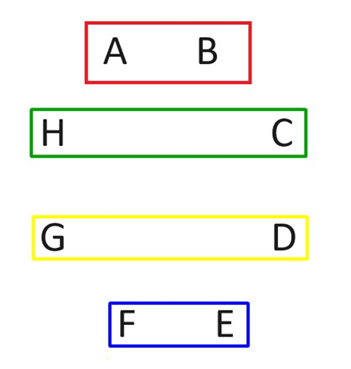
第二輪,保持玩家A的位置不變。然後其他人順時針旋轉,如下圖所示。
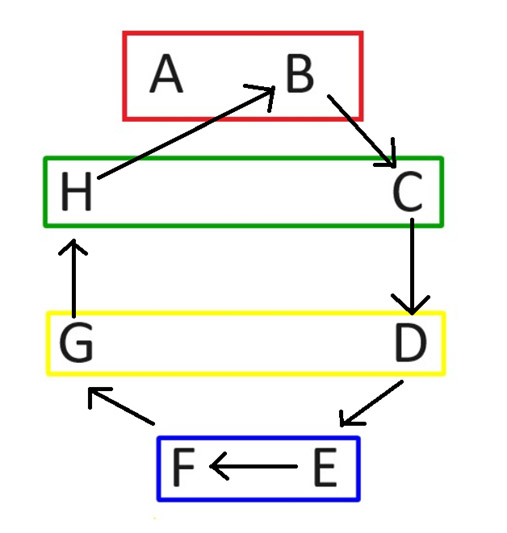
經過輪換,第二輪比賽安排如下:
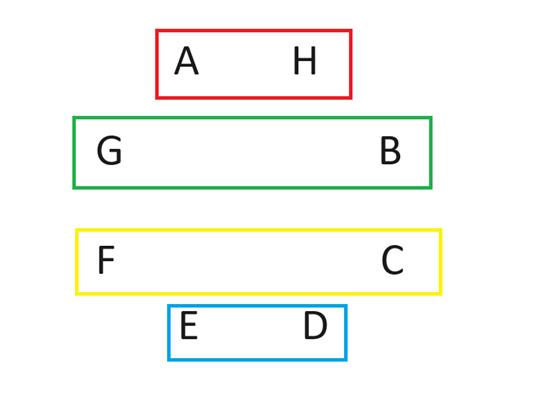
重複此動作,直到每個人都和玩家 A 交手。我無法解釋為什麼這種方法有效,但它確實有效。這種方法適用於任何偶數玩家。想了解更多相關討論,請搜尋「循環法」和「循環賽」。
下表列出了八人情況下的所有對陣情況。注意,每個人都只與其他人交手一次。
| 圓形的 | 玩家 1 | 玩家 2 |
|---|---|---|
| 1 | 一個 | B |
| 1 | 哈 | C |
| 1 | 格 | D |
| 1 | F | 埃 |
| 1 | 一個 | 哈 |
| 2 | 格 | B |
| 2 | F | C |
| 2 | 埃 | D |
| 3 | 一個 | 格 |
| 3 | F | 哈 |
| 3 | 埃 | B |
| 3 | D | C |
| 4 | 一個 | F |
| 4 | 埃 | 格 |
| 4 | D | 哈 |
| 4 | C | B |
| 5 | 一個 | 埃 |
| 5 | D | F |
| 5 | C | 格 |
| 5 | B | 哈 |
| 6 | 一個 | D |
| 6 | C | 埃 |
| 6 | B | F |
| 6 | 哈 | 格 |
| 7 | 一個 | C |
| 7 | B | D |
| 7 | 哈 | 埃 |
| 7 | 格 | F |
如果玩家人數為奇數,只需在錦標賽中新增一名虛擬玩家,即可獲得偶數。與虛擬玩家對戰的玩家將獲得該輪輪空資格,這意味著該玩家無需參加比賽。因此,每個人都會有一輪輪空。以下是七人錦標賽的輪空規則。
| 圓形的 | 玩家 1 | 玩家 2 |
|---|---|---|
| 1 | 一個 | B |
| 1 | 再見 | C |
| 1 | 格 | D |
| 1 | F | 埃 |
| 2 | 一個 | 再見 |
| 2 | 格 | B |
| 2 | F | C |
| 2 | 埃 | D |
| 3 | 一個 | 格 |
| 3 | F | 再見 |
| 3 | 埃 | B |
| 3 | D | C |
| 4 | 一個 | F |
| 4 | 埃 | 格 |
| 4 | D | 再見 |
| 4 | C | B |
| 5 | 一個 | 埃 |
| 5 | D | F |
| 5 | C | 格 |
| 5 | B | 再見 |
| 6 | 一個 | D |
| 6 | C | 埃 |
| 6 | B | F |
| 6 | 再見 | 格 |
| 7 | 一個 | C |
| 7 | B | D |
| 7 | 再見 | 埃 |
| 7 | 格 | F |
最後,假設這是一場網球錦標賽,每個球場都有好球面和壞球面。壞球面可能朝向太陽。有什麼公平的方法可以確保每個球員獲得好球面和壞球面的次數相同?
為了解決這個問題,我提議使用《生活大爆炸》中解釋的「蜥蜴史波克擴展」。這種石頭剪刀布的玩法適用於任何奇數個符號。為了公平地確定哪位玩家拿到了好牌,我們考慮七人的情況。下圖顯示了哪位玩家拿到了好牌,箭頭指向拿到壞牌的玩家。
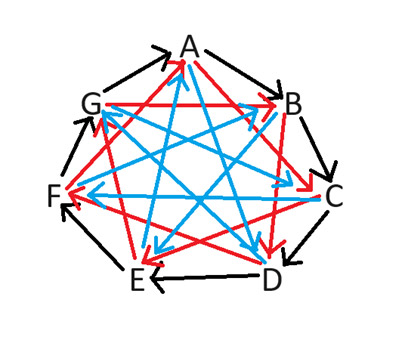
例如,如果玩家 B 和 D 玩牌,B 會佔好牌,因為他們之間的箭頭指向 D。不難看出我是如何畫圖的。箭頭總是順時針方向。我們需要為從 1 到 3 的所有可能的空位數都畫出箭頭。
然而,我們不需要畫出這樣的圖,只需要畫一個字母環。考慮兩種順時針繞圈從一個玩家到另一個玩家的方法。步數較少的路線將獲得好方。考慮B和F之間的一局遊戲。順時針方向,從B到4要四步,從F到B要三步。由於三小於四,所以F獲得好方。
下表顯示了七人循環賽中所有可能的對陣情況,包括哪些球員佔據優勢,哪些球員佔據劣勢。
| 圓形的 | 好的一面 | 壞的一面 |
|---|---|---|
| 1 | 一個 | B |
| 1 | C | 再見 |
| 1 | D | 格 |
| 1 | 埃 | F |
| 2 | 一個 | 再見 |
| 2 | 格 | B |
| 2 | C | F |
| 2 | D | 埃 |
| 3 | 格 | 一個 |
| 3 | F | 再見 |
| 3 | B | 埃 |
| 3 | C | D |
| 4 | F | 一個 |
| 4 | 埃 | 格 |
| 4 | D | 再見 |
| 4 | B | C |
| 5 | 埃 | 一個 |
| 5 | D | F |
| 5 | 格 | C |
| 5 | B | 再見 |
| 6 | 一個 | D |
| 6 | C | 埃 |
| 6 | F | B |
| 6 | 格 | 再見 |
| 7 | 一個 | C |
| 7 | B | D |
| 7 | 埃 | 再見 |
| 7 | F | 格 |
不幸的是,這種平衡策略在玩家人數為偶數時不起作用。這是因為當兩名玩家位於圓圈正對面時,圓圈周圍的距離是相同的。如果必須如此,可以將這種方法用於所有其他比賽,但玩家必須在圓圈上相距180度時隨機分配。
我暫時就此話題進行探討。我保留在未來的新聞通訊中進一步闡述的權利。未來可能討論的主題包括三名或三名以上球員的比賽,以及使用多塊球場以平衡每位球員在每塊球場上的出場頻率。
最後,祝大家光明節快樂!


