證明調和級數發散
本週的證明是調和級數收斂。不過,在此之前,我先帶給大家每週例行的邏輯謎題。
邏輯謎題
星期一,醫院育嬰室有兩個嬰兒,一男一女。
週二,家中添了一名新生兒。
週三隨機抽取一名嬰兒,是個男孩。
星期二出生的嬰兒是男孩的機率是多少?
證明調和級數發散
調和級數是所有整數的逆的集合。換句話說, 11 , 12 , 13 , 14 ,6; font-family: 'Open Sans', sans-serif; color: #313131 !important;"> 1 5 ,…, 1 ∞ 。如果一個級數的所有元素之和為無窮大,則稱該級數發散。對於調和級數而言,這一點並不大
方法一:比較檢驗
如果我能證明另一個元素相等或更少的級數是發散的,那麼調和級數也必然是發散的。
諧波序列: 11,12,13,14,15,16 ,6; font-family: 'Open Sans', sans-serif; color: #313131 !important;"> 1 7 , 1 8 , 1 9 , 1 10 , 1 11 , 1 12 , 1 13 ,…, 1 ∞ ∞ .
系列 2: 1 1,1 2 ,6; font-family: 'Open Sans', sans-serif; color: #313131 !important;"> 1 4 , 1 4 , 1 8 , 1 8 , 1 8 , 1 8 , 1 16 , 1 16 , 1 8 , 1 8 , 1 16 , 1 16 , 1 1, 11 , 11 , 16; font-family: 'Open Sans', sans-serif; color: #313131 !important;"> 1 16 , 1 16 , 1 16 , 1 32 ,…, 1 ∞ .
級數 2 與調和級數一樣,都以相同的兩個元素開始。然後,對於每個 n>=2,它重複1 / 2n × 2n-1次。請注意,級數 2 中的每個元素都小於或等於調和級數中的對應元素。級數 2 可分成若干組,每組總和為1 / 2n × 2n-1 = 1/2 。讓我用不同的顏色來說明每一組:
系列 2: 1 1 ,6; font-family: 'Open Sans', sans-serif; color: #313131 !important;"> 1 2 , 1 4 , 1 4 , 1 8 , 1 8 , 1 8 , 1 8 , 1 16 , 1 8 , 1 8 , 1 8 , 1 16 , 1 1 1 , 1 1 16; font-family: 'Open Sans', sans-serif; color: #00A0D1 !important;"> 1 16 , 1 16 , 1 16 , 1 16 , 1 32 (16 次), 1 64 (32 次) …
1 + ( 1 2 X ∞) = ∞
方法二:微積分
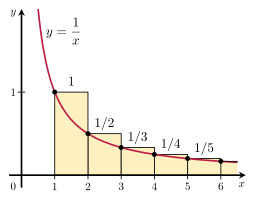
請注意,黃色矩形的面積大於紅色曲線下的面積。紅色曲線下的面積為:
∫ 1 ∞ 1 x dx = ln(x) + c 從 1 到 ∞ = ln(∞) + c – ln(1) – c = ∞。
邏輯謎題解答
簡答題
對於發生的事情有兩種可能的解釋,我們暫且稱它們為X和Y。
X = 週二新增一名男孩,週三觀察到一名男孩。這種情況發生的機率為 (1/2)*(2/3) = 2/6 = 1/3。
Y = 週二新增一名女孩,週三觀察到一名男孩。這種情況發生的機率為 (1/2)*(1/3) = 1/6。
X+Y = 1/3 + 1/6 = 1/2
問題是問兩種情況同時發生的機率是多少,X 是實際發生的事情。機率計算公式為 X/(X+Y) = (1/3)/(1/2) = 2/3。
長答案
貝葉斯條件機率公式指出,Prob(A 在 B 的條件下) = Prob(A 且 B)/Prob(B),其中 prob(x) 表示事件 x 發生的機率。令:
A = 男孩,週二加入
6; font-family: 'Open Sans', sans-serif; color: #313131 !important; ">B = 週三觀察到的男孩在這種情況下:
Prob(A 已知 B) = Prob(週二添加的男孩已知週三觀察到的男孩) = Prob(週二添加的男孩且週三觀察到的男孩)/Prob(週三觀察到的男孩)。
在沒有任何關於週二抽籤結果的資訊的情況下,週二抽出的嬰兒有50%的機率是男孩。假設週二抽出的嬰兒是男孩,那麼週三抽出的嬰兒有2/3的機率是男孩。
同樣,在沒有任何關於週二抽籤資訊的情況下,週二抽到女孩的機率為50%。假設週二抽到的嬰兒是女孩,那麼週三抽到的嬰兒是男孩的機率為1/3。
週三抽到男孩的機率等於 prob(週二加入的男孩)*prob(週三抽到的男孩) + prob(週二加入的女孩)*prob(週三抽到的男孩) = (1/2)*(2/3) + (1/2)*(1/3) = 1/2。
星期二加入一個男孩,星期三抽出一個男孩的機率 = (1/2)*(2/3) = 1/3。
因此,答案是 (1/3)/(1/2) = 2/3。


