勾股定理的證明
本週,我將證明經典的勾股定理,即直角三角形兩直角邊平方和等於斜邊平方。最著名的例子是邊長分別為 3、4 和 5 的直角三角形。注意3² + 4² = 5² 。不過,在此之前,我先帶給大家每週例行的邏輯謎題。
邏輯謎題
一位心不在焉的古代哲學家忘記為掛在屋子牆上的大鐘上弦。他沒有收音機、電視、電話、互聯網,也沒有其他計時工具。於是,他沿著筆直的沙漠公路步行幾英里,去拜訪朋友。他在朋友家住了一晚,回來時,他已經知道如何調好鐘了。他是怎麼知道的呢?
答案在簡報末尾。
勾股定理的證明
請看下圖,它由一個被分成四個全等直角三角形的大正方形和一個位於中間的小正方形組成。中間之所以會有一個小正方形,是因為任一三角形的內角和是 180 度。我在2025 年 11 月 13 日的簡報中證明了這一點。
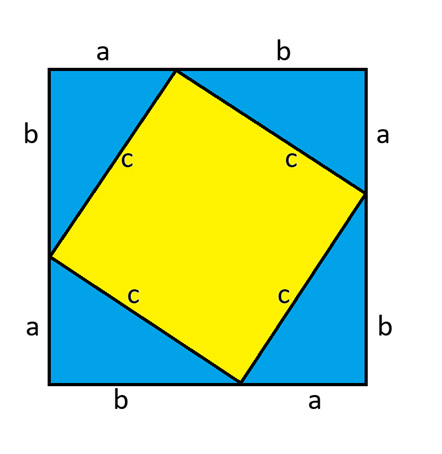
大正方形的面積為 (a+b) ² 。每個三角形的面積為ab² 。中間黃色正方形的面積為c² 。將大正方形的面積等於其內部各部分面積總和,我們得到:
6; font-family: 'Open Sans', sans-serif; color: #313131 !important;">(a+b) 2 = 4 ab 2 + c 2
a² + 2ab + b² = 2ab + c²
兩邊同時減去 2ab,得到:
a² + b² = c²
邏輯謎題解答
- 教授給鐘上了發條,然後隨意設定了一個時間。
- 當他到達朋友家時,他記下了到達時間。
- 離開時,他會記下離開的時間,並從離開的時間中減去到達的時間來計算在朋友家停留的時間。
- 他小心翼翼地以去朋友家時的速度回來。
- 當他回到家時,他的時鐘會顯示他在朋友家的時間加上步行時間。他可以從總時間中減去在朋友家的時間來計算步行時間。然後,他可以將總步行時間除以 2 來計算單程時間。
- 然後他可以將時鐘設定為離開朋友家的時間加上單程步行時間。
我們來看一個例子。
他把錯誤的鐘錶上緊了發條,並調到了12點。實際時間是8點,他到達朋友家。 1點他離開,記下這次拜訪花了5個小時。回來時,他發現自己的鐘錶顯示8點。減去5小時的拜訪時間,代表他總共走了3個小時。也就是說,單程花了1.5個小時。如果他1點出發,走了1.5個小時,那麼現在應該是2點30分,於是他把鐘錶調到了2點30分。


