如何應用 PEMDAS 規則。
如果你跟我一樣,你的Facebook直播裡肯定會有無數關於運算順序的問題。在所有這些問題之後,評論區裡都會有數百個答案,而這些答案中大多數都是錯的。承認自己錯了的人,卻始終為零。
我的觀點為什麼正確?首先,如果可以自吹自擂的話,我想我是公認的賭場遊戲數學領域的領導者。搜尋任何賭場遊戲或術語,你都會到處看到我的名字。除此之外,我擁有加州大學聖塔芭芭拉分校的數學和經濟學學位,並且是精算師協會的退休會員。大學畢業後,我從事的所有工作都與數學息息相關。
此類問題的例子是:
6÷2(1+2)=?
暫停片刻並解決它。

如果你的答案是 1,那你就錯了。我懷疑你錯的原因是,你遵循的是 PEMDAS 的運算順序經驗法則。這是五年級左右教的記憶技巧。我學到的記憶方法是「請原諒我親愛的莎莉阿姨」。它的目的是教導孩子們按照以下順序計算表達式的值:
- 1.括號
- 2.指數
- 3.乘法
- 4.除法
- 5.算術
- 6.減法
你的小學老師可能真的相信這是正確的。然而,事實並非如此。我不知道它是怎麼來的,但我懷疑這是一種簡化的記憶方法,10歲的孩子很容易理解。任何事物的簡化都存在一個問題:雖然大多數情況下它都能得到正確答案,但通常也存在例外。在 PEMDAS 的情況下,它將引導人們以這種方式解決前面提到的 6 ÷ 2(1 + 2)問題:
- 6 ÷ 2 (1 + 2) = 6 ÷ 2 (3)因為先求括號
- 6 ÷ 2 (3) = 6 ÷ 2 × 3 ,因為括號外的運算子不表示乘法
- 6 ÷ 2 × 3 = 6 ÷ 6 ,因為依照 PEMDAS,乘法先於除法進行
- 6÷6=1
上述邏輯的錯誤在於第三步。乘法並不總是先於除法。它們的優先順序相同。當兩者出現在同一個表達式中時,先執行左邊那個。
我想補充一下,加法也不一定要先於減法。它們的優先順序也相同。不過,在加減運算中,由於較高的規則不適用,所以先做哪一個都沒關係。
以下是計算 6 ÷ 2 (1 + 2) 的正確方法:
- 6 ÷ 2 (1 + 2) = 6 ÷ 2 (3)因為先求括號
- 6 ÷ 2 (3) = 6 ÷ 2 × 3,因為括號外沒有運算子表示乘法
- 6 ÷ 2 × 3 = 3 × 3因為乘法和除法都是先從左邊計算
- 3 × 3 = 9
這裡還有另一個問題想問您:
7 + 7 ÷ 7 + 7 × 7 – 7 = ?
在 Facebook 上,你會看到答案是 56。人們之所以會犯錯,並不是因為 PEMDAS,而是因為「我的計算器說答案是 56」。這是那些只是從左到右計算的人給出的懶惰且錯誤的答案。不正確的推理是:
- 7 + 7 ÷ 7 + 7 × 7 – 7 = 14 ÷ 7 + 7 × 7 – 7因為先從左邊求值
- 14 ÷ 7 + 7 × 7 – 7 = 2 + 7 × 7 – 7因為先從左邊求值
- 2 + 7 × 7 – 7 = 9 × 7 – 7因為先從左邊求值
- 9 × 7 – 7 = 63 – 7 ,因為先從左邊計算
- 63 – 7 = 56
正確評價這個的方法是:
- 7 + 7 ÷ 7 + 7 × 7 – 7 = 7 + 1 + 7 × 7 – 7 ,因為除法優先於加法,並且位於乘法的左邊
- 7 + 1 + 7 × 7 – 7 = 7 + 1 + 49 – 7 ,因為乘法取代了加法和減法
- 7 + 1 + 49 – 7 = 8 + 49 – 7因為加法和減法之間先進行最左邊的運算
- 8 + 49 – 7 = 57 – 7因為加法和減法之間先進行最左邊的運算
- 57 – 7 = 50
注意,PEMDAS 在這方面做得很好。人們之所以會犯錯,是因為沒有正確使用計算機。以正確的順序輸入數字和運算至關重要。使用逆波蘭表示法的計算器(例如 HP15C)更容易做到這一點。順便說一句,任何擁有 HP15C 或 12C 的人都會立即成為我的朋友。
最後,我想用我自己創作的這個謎題來為這些運算順序謎題增添一些新意,包括謎題的邏輯和佈局。我承認我從谷歌上偷了圖片。這個謎題的靈感來自於Mind Your Decisions YouTube頻道上一個類似但更難的謎題。請隨意發布它;我希望它能火起來。
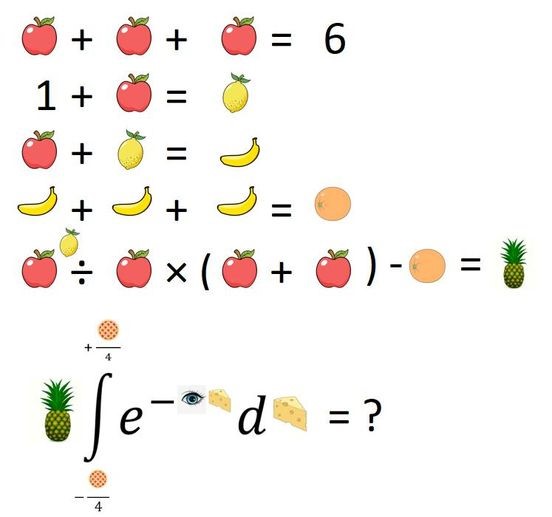
僅解決菠蘿問題可獲得部分積分,解決積分問題可獲得全部積分。
我會在6月29日的簡報中公佈答案。在此之前,祝你好運常伴左右。


