大型 Zoom Call 數學謎題
以下是我上週在新聞通訊中提出的一個問題。如果你需要提醒,可以參考一下。
問題
假設美國眾議院所有 435 名有投票權的議員都參加了同一場 Zoom 會議,會議時間定於上午 9 點至 10 點。然而,會議無需全程參與,只需參與其中的一部分即可。每位議員都會隨機選擇一個確切的時間,在一小時的範圍內加入和退出會議。
至少有一位代表在通話中與其他所有代表重疊的機率是多少?換句話說,在通話期間看到其他每位成員的臉,不一定是同時看到所有人的臉。
請捲動瀏覽這些圖片以查看我的答案和解決方案。

回答
2/3
解決方案
對於涉及大量人群的問題,我的一般策略是先問兩個人。找到答案後,我會問三個人。然後,如果問題不太難,我會問四個人。如果我發現了一個規律,那麼這個規律很可能適用於任何人數。
基礎數學複習
在進一步講解之前,我先來頻繁地使用一下 combin(x,y) 函數。它表示從一組 x 項中選擇 y 項的方法數。例如,從 52 張牌中選擇 5 張(順序不重要)的方法數為 combin(52,5) = 2,598,960。答案可以表示為 x! / (y! * (xy)!)。
在這種情況下,感嘆號並不意味著我在喊叫,而是代表階乘函數。這是對給定數量的物品進行排序的方法數。例如,如果您需要一次閱讀一本六本書,那麼可能的書籍排序數就是 6!。對於一般情況下的 n,答案是 1*2*3*…*n。對於六本書的情況,答案是 1*2*3*4*5*6 = 720。
雙人案例
話雖如此,我們來解決這個問題,因為兩個人通話的具體時間並不重要,重要的是事件發生的順序。我們用一個字母來表示某個人進入/離開通話。從左邊開始,第一個字母代表進入通話,第二個字母代表離開通話。
6;font-family: 'Open Sans',sans-serif;color: #313131!important">在通話記錄的四個位置中,有 6 種組合方式可以放置字母 A:1. AABB
2. ABAB
3. ABBA
4. BAAB
5.巴巴
6. BBAA
讓我們檢查一下在每種情況下兩個呼叫者是否同時在線:
1. AABB – 否,A 在 B 加入通話前就來了並且離開了。
2. ABAB-是的,B 到達和 A 離開之間有重疊。
3. ABBA-是的,B 到達和 B 離開之間有重疊。
4. BAAB — 是的,A 到達和 A 離開之間有重疊。
5. BABA-是的,A 到達和 B 離開之間有重疊。
6. BBAA - 否,B 在 A 加入通話之前就來了並且離開了。
每種情況發生的可能性均等。六種情況中有四種有重疊,因此在兩人情況下重疊的機率為 2/3。
三人案
在三人情況下,通話記錄的數量等於 A 從歷史記錄中的 6 個位置中選擇 2 個位置的方式數與 B 從剩餘 4 個位置中選擇 2 個位置的方式數的乘積。這等於 combin(6,2)*combin(4,2) = 15*6 = 90。
列出所有 90 個人會很繁瑣。為了簡化流程,我們假設 A 先加入。一定有人是第一個,所以 A 也行。
首先,我們假設通話記錄中的下一個事件是 A 離開。我們將其表示為 AA????。無論 B 和 C 如何進入和離開通話,都不會有人與 A 重疊。因此,AA 場景的成功機率為 0。 AA 場景本身的機率為 1/5,因為在 A 佔據第一個位置後,接下來可能發生的事件有五種:A、B、B、C 和 C。
其次,我們考慮 A 先加入,B 隨後進入,然後 A 離開的情況。在這種情況下,B 代表 A 以外的任何人(已結束通話)。這表示為 ABA???。其餘待放置的字母是 B、C 和 C。 B 的放置方式有三種(BCC、CBC 和 CCB),其中 CBC 和 CCB 會導致 B 與 A 和 C 重疊。因此,ABA 情境下成功的機率為 2/3。此情境本身的機率為 pr(除 A 外的任何人加入)*pr(A 離開) = (4/5)*(1/4) = 1/5,其中 pr(x) 表示事件 x 的機率。
第三,我們考慮 A 先加入,B 隨後進入,然後 B 離開的情況。這種情況表示為 ABB???。剩餘待放置的字母為 A、C 和 C。 A 的置入方式有三種(ACC、CAC 和 CCA),其中 CAC 和 CCA 會導致 A 與 B 和 C 重疊。因此,ABB 方案的成功機率為 2/3。此方案本身的機率為 pr(A 以外的任何人加入)*pr(B 離開) = (4/5)*(1/4) = 1/5。
第四,我們考慮 A 先加入,B 隨後加入,然後 C 加入的情況。這種情況可以用 ABC 表示嗎?剩下需要放置的字母分別是 A、B 和 C。很容易看出,A 離開通話時,B 和 C 的位置都會重疊。因此,在這種情況下成功的機率為 1。這種情況本身的機率是 pr(A 以外的任何人加入)*pr(第三人加入) = (4/5)*(2/4) = 2/5。
我們考慮了所有可能的情況,機率 (1/5 + 1/5 + 1/5 + 2/5) 加起來等於 1。將每種情況的機率與其成功機率的點積相加,我們得到:(1/5)*0 + (1/5)*(2/3) + (1/5)*(2/3) + (2/5)*1 = 0 + 2/15 + 2/15 + 6/15 = 10/15 = 2/3。
四人案例
如果時間緊迫,我可能會猜原題的答案是 2/3,因為它適用於 2 人和 3 人的情況。然而,這似乎不太令人滿意,所以讓我們來討論一下 4 人的情況。我可以將其分解為十種可能的情況,如下所示:
- AA??????
情境機率 = 1/7
成功機率 = 0(沒有人可以重疊 A)
- ABA? ? ?
情境機率 = 1/7
成功機率 = 16/30
- ABBA? ? ?
情境機率 = 1/35
成功機率 = 0(沒有人可以重疊 B)
- ABBC? ? ?
情境機率 = 4/35
成功機率 = 2/3
- ABCA? ? ?
情境機率 = 4/35
成功機率 = 5/6
- ABCBA? ? ?
情境機率 = 1/35
成功機率 = 2/3
- ABCBC? ? ?
情境機率 = 1/35
成功機率 = 2/3
- ABCBD? ? ?
情境機率 = 2/35
成功機率 = 1(A 將與 B、C 和 D 重疊)
- ABCC? ? ?
情境機率 = 4/35
成功機率 = 5/6
- ABCD? ? ?
情境機率 = 8/35
成功機率 = 1(A 將與 B、C 和 D 重疊)
我很抱歉沒有仔細地計算每種情況的數學計算,但我不希望這個解決方案運行太長時間,並希望將一些工作留給讀者。
下表總結了四人案例的所有十種情景。
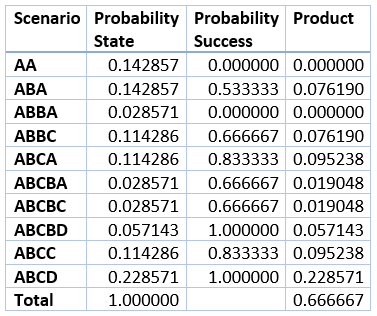
表格右下角的儲存格顯示機率為 2/3。
概括
6;font-family: 'Open Sans',sans-serif;color: #313131!important">我們已經證明了,對於兩人、三人和四人的情況,概率都是2/3。可以推斷,無論人數多少,這個概率可能都會保持不變。一些比我更聰明的人通過模擬和數學計算證實了這一點。

