圓週角定理證明(第二部)
你可能還記得,上週我開始證明圓週角定理。這週,我們將完成它。不過,在此之前,我先帶給大家我每週的例行邏輯謎題。
邏輯謎題
下列哪些敘述是正確的?
- 這些說法中有一條是錯誤的。
- 這兩項陳述中有兩項是錯誤的。
- 這三項陳述是錯誤的。
- 這四項陳述中有四項是錯誤的。
- 這五項陳述是錯誤的。
- 這六項陳述是錯誤的。
- 這七項陳述都是錯的。
- 這八項陳述是錯誤的。
- 這九條陳述都是錯的。
- 這十條陳述是錯誤的。
答案在簡報底部。
圓週角定理(第二部)
讓我來提醒你圓周角定理的內容。
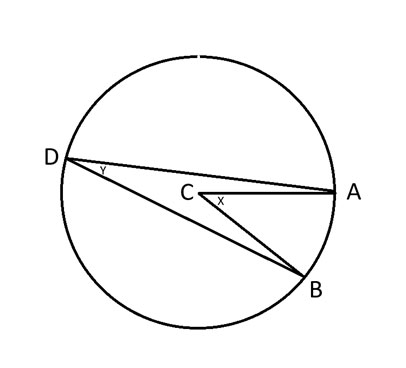
A、B、D = 圓上的任三點。
C = 圓心。
x = 角 ACB。
y = 角度 ADB。
圓週角定理指出,角 2y = x。
上週我證明了當 AD 或 BD 構成圓的直徑時,這個結論成立。本週我將以此為例,證明該定理對於 D 的一般情況也成立。
我將按如下方式列出D的所有可能位置:
情況 1 = AD 或 BD 構成圓的直徑(上週已證明)
情況 2 = D 位於(或說「位於」?)圓弧上,與 A 和 B 相對。
情況 3 = 所有其他情況
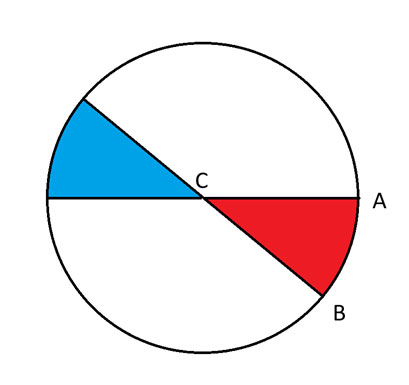
換句話說,情況 2 將涵蓋 D 位於藍色區域內圓週邊緣的情況。情況 3 將涵蓋 D 位於藍色區域之外的其他位置的情況。
讓我們用下圖來討論。
讓:
x = x1 + x2
y = y1 + y2
z = z1 + z2
我們努力證明 x = 2y
我仔細地從D點到C點畫了一條線,這條線構成了圓的直徑。 E點是它與圓的另一邊相交的點。
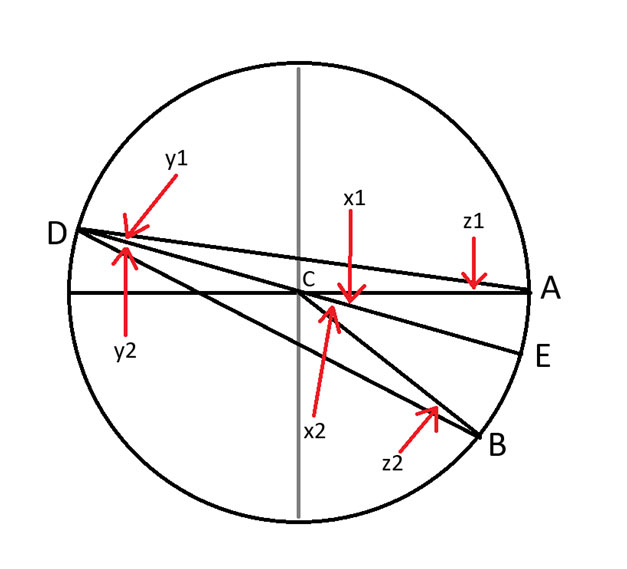
角度中的數字應該要加下標,但是我的繪圖軟體不允許。
考慮三角形 ADE。
由於 DE 構成直徑,我們可以利用上週證明的結論來證明 2x1 = 2y1。
現在考慮三角形EDB。
依照同樣的邏輯, 2x² = y² 。
將下列方程式相加:
2x₁ + 2x₂ = y₁ + y₂
2( x₁ + x₂ ) = y₁ + y₂
2x = y
案例二就講完了。
我們來看案例 3。

在這裡,我們努力證明 2x 1 = y 1 。
案例1:
2x² = y²
2(x 1 + x 2 ) = y< 1 +y 2
將下面的等式減去上面的等式:
2x 1 = y 1
我們已經證明了第三種情況。
邏輯謎題答案
只有第9條是正確的。
邏輯謎題解答
我們有十個互相矛盾的說法。如果十個人各執一詞,要嘛只有一個人是對的,要嘛所有人都是錯的。
我們考慮十個陳述全部為假的情況。這樣一來,第十個陳述就為真。這意味著只有九個陳述為假。因此,這構成矛盾。必然存在一個為真的陳述。但究竟是哪一個呢?
如果其中一條陳述為真,則其餘九條陳述均為假。正是第九條陳述表明了這一點。因此,只有第九條陳述為真。


