圓週角定理證明(第一部分)
本週我們繼續我的數學定理證明主題。本週的定理是圓週角定理。這個證明比以往的要複雜一些,所以我將把它分成兩部分,第二部分下週發布。不過,在此之前,我先帶給大家我每週的例行邏輯謎題。
邏輯謎題
在下圖所示的示意圖中,移動一枚硬幣,使其形成兩排各四枚硬幣的直線。
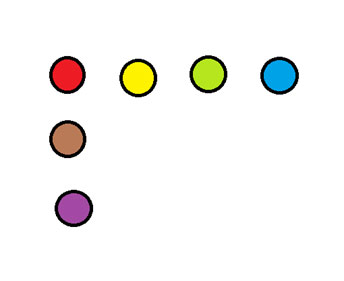
答案在簡報底部。
圓週角定理證明(第一部分)
在解釋圓週角定理之前,讓我先定義下圖所示的圓上的一些點。
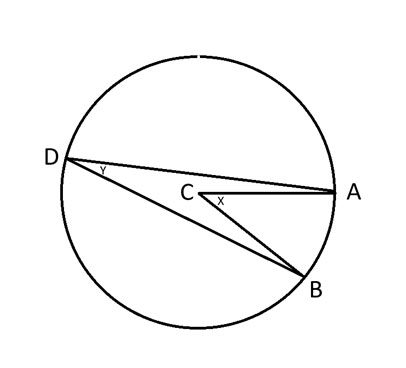
A、B、D = 圓上的任三點。
C = 圓心。
x = 角 ACB。
y = 角度 ADB。
圓週角定理指出,角 2y = x。
在本期簡報中,我將嘗試證明 AD 或 BD 構成圓的直徑這一特定情況。下週,我將擴展討論 D 位置的一般情況。
我們將 AD 構成圓的直徑這一特殊情況稱為情況 1。下面是這種情況的新圖。
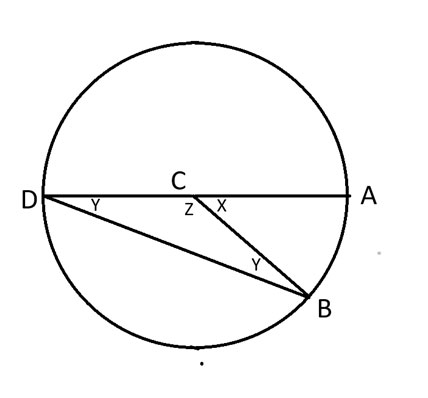
在上圖中,AD 構成以 C 為圓心的圓的直徑。
我們可以說 x+z = 180 度,因為它們構成了圓週 360 度的一半。
∠BCD 構成等腰三角形。因此,∠CDB = ∠CBD = y。
正如我在2025年11月13日的簡報中所證明的,三角形內角和等於180度。換句話說,z + 2y = 180度。
讓我們重寫這兩個方程式:
z = 180 – x
z = 180 – 2y
讓我們把它們都寫成方程,因為它們都等於 z。
180 – x = 180 – 2y
-x = -2y
x = 2y。
我們已經證明了圓週角定理的一個特例,即圓上兩點構成直徑的情況。下週我們將以此為基礎,證明圓週角定理的一般情況。
邏輯謎題解答
將藍色硬幣移到紅色硬幣上方。下圖中的數字表示每堆硬幣的數量。
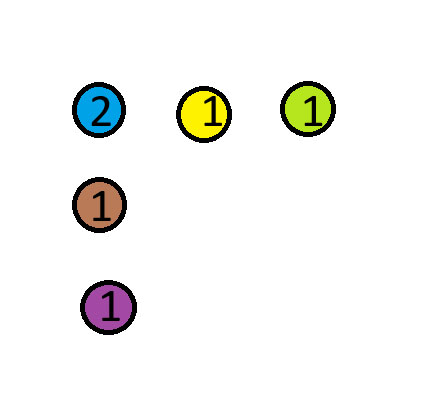
致謝:我從「Mind Your Decisions」 YouTube頻道獲得了這個謎題。這是連結影片中的第三個謎題。


