如何玩國際象棋評分規則
本週我們將探討一種利用棋局評分公式來提升等級的方法,但前提是你的棋藝絲毫不會提高。要注意的是,這只能帶來一點小小的優勢,主要還是出於學術興趣。不過,在此之前,和往常一樣,我會先展示我們每週的邏輯謎題。
邏輯謎題
50個人排成一排,依序編號1到50。排在第一位的人是1號。每個人要不是總是說真話,就是總是說謊。每個人都知道其他人說的是真話。
所有偶數的人都說:“在我面前的每個人都是騙子。”
所有奇數的人都說:“我身後的人都是騙子。”
誰在說實話?
如何玩國際象棋評分規則

據我所知,最常見的西洋棋等級分系統是Elo等級分系統。它以Arphad Elo的名字命名。其他遊戲和體育運動也使用同樣的系統。
它的工作原理基本上是,根據雙方玩家的等級分,用一個公式確定任意玩家獲勝的機率。獲勝的玩家將根據其輸掉比賽的機率獲得相應的分數。同樣,輸掉比賽的玩家也將根據其獲勝的機率獲得相應的分數。獲勝得1分,平手得0.5分,平手得0分。
該系統基於一個我同意的假設,即球員的表現可以根據鐘形曲線上繪製的隨機數來建模,並以球員的得分作為平均值。獲得較大數字的玩家獲勝。
獲勝機率的決定方式如下:
令 r1 = 玩家 1 的評分。
令 r2 = 玩家 2 的評分。
p = 玩家 1 獲勝的機率。
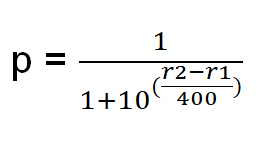
我們來看一個例子。設 r1=1900,r2=2000。
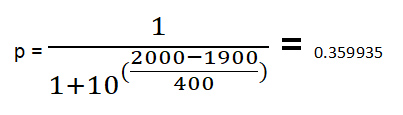
假設勝一場得1分,負一場得0分,則得分增加32*(實際分數-勝率)。
在我們上面的例子中,如果玩家1輸了(正如預測的那樣),那麼他的等級分會下降11.52分,而玩家2的等級分會上升相同的數字。如果玩家1獲勝,他的等級分會上升20.48分,而玩家2的等級分會下降相同的數字。
Elo 等級分方案是基於績效的標準差,如上文所述的隨機數方法建模的那樣,該標準差為 200。我假設這是正確的。然而,Elo 等級分錶所基於的獲勝機率公式與該標準差並不一致,除非評級差異為 0 或 189。
具有 r1 等級的玩家獲勝的正確機率是:
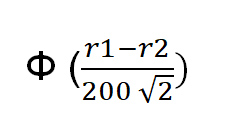
其中函數 Φ(x) = 隨機標準常態變數小於 x 的機率。在 Excel 中,正確的公式為 norm.s.dist((r1-r2)/(200*sqrt(2)),1)。
讓我們來看一個等級分差距為100的情況。假設玩家1處於劣勢。 Elo公式顯示玩家1獲勝的機率為35.99%。然而,基於200的標準差,他的實際獲勝機率為36.18%。換句話說,玩家1贏得比賽對玩家2來說是個好的選擇,但對玩家2來說則是個不好的選擇。我顯示玩家1的等級分預期收益和玩家2的預期損失均為0.06分。
接下來我們來看看300分的等級分差距,其中玩家1處於劣勢。根據Elo公式,玩家1獲勝的機率為15.10%,而我給出的數值是14.44%。這意味著,對於玩家1來說,贏得比賽是一個糟糕的選擇,而對於玩家2來說,則是一個不錯的選擇。玩家1的預期損失為0.21分,而玩家2的預期收益為0.21分。
實際機率背後的數學是基於高斯曲線,並且比我在本期通訊中想要討論的內容更為複雜。
底線是,如果評分差距超過189,那麼熱門球隊贏得比賽是一個不錯的選擇。同樣,如果評分差距小於189,那麼弱勢球隊贏得比賽也是一個不錯的選擇。
然而,這種偏見相當小。我不會根據這些資訊接受或拒絕任何比賽。相反,我認為你應該出於對國際象棋的熱愛而接受任何比賽。
延伸閱讀:維基百科關於 Elo 評級系統的文章。

邏輯謎題答案
只有 2 號人和 49 號人說的是實話。
邏輯謎題解答
我們先從第 1 個人說起。如果他說的是真話,那麼其他人都在說謊。然而,第 3 個人說,從 4 歲到 50 歲的人都在說謊。如果這是真的,那麼第三人說的是真話。然而,第一人說他在說謊。這就導致了矛盾。因此,第一人肯定在說謊。
第二個人只說第一個人在說謊。這說明第二個人說的是真話。
從4到50,每個偶數人都說2號人在說謊。這樣一來,他們就全都是騙子了。
49號說50號在說謊,這是真的。這就意味著49號說的是真話。
從3到47號奇數人,每個都說49號人在說謊。也就是說,他們都是騙子。
因此,說真話的人只有 2 號和 49 號。


