能被 3 整除的證明

本週我打算暫時放下總統冷知識，嘗試一些新的東西。我一直很喜歡數學證明。在靈感枯竭之前，我會先講解一些著名的數學定理，並儘可能用簡單易懂的方式解釋它們的正確性。首先，本週我將證明：如果一個整數的各位數字和能被3整除，那麼這個整數本身也能被3整除。不過，在此之前，我先奉上每週例行的邏輯謎題。

邏輯謎題

桌上有四張牌。你可以看到正面朝上的牌分別標示 D、K、3 和 7。你知道每張牌的一面是字母，另一面是數字。據說有一張生產規則：一面是 D 的牌，另一面必須是 3。為了驗證這條規則是否被遵守，你需要翻開哪兩張牌？

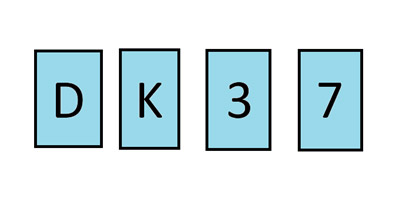
答案將在簡報最後揭曉。

能被 3 整除的證明

如引言所述，可以如下檢驗一個整數是否能被 3 整除：

例如，我們來看白宮的電話號碼，即 2024567041。這幾個數字總和為 2+0+2+4+5+6+7+0+4+1 = 31。31 不能被 3 整除，因此原號碼也不能被 3 整除。

為了證明這種方法有效，請如下分解原始數字：

6; font-family: 'Open Sans', sans-serif; color: #313131 !important; ">2024567041 = (2*1000000000) + 0 + (2*10000000) + (4*10000 + (4*10) + (1*1)

接下來，將 10 的冪分成兩部分，一部分是 1，另一部分是其餘部分：

= (2*(999999999+1)) + 0 + (2*(9999999+1)) + (4*(999999+1)) + (5*(99999+1)) + (7*(9999+1)) + 0 + (4*(9+1)) + (7*(9999+1)) + 0 + (4*(9+1) ++)

顯然，任何由 9 組成的數字都能被 3 和 9 整除。例如，99999 = 3 * 33333。

也就是說，讓我們重新排列上面數字中的各項。

= (2*999999999) + (2*9999999) + (4*999999) + (5*99999) + (7*9999) + (4*9) + (1*0) + (2*1) + (2*1) + (4*1) + (51.

前七項中的每一項顯然都能被 3 整除，因為它們都能被一個由 9 組成的數整除。換句話說，(2*999999999) + (2*9999999) + (4*99999) + (5*99999) + (7*9999) + (4*9) + (1*0) 能被 9 整除，所以我們可以去掉 9 的部分。剩下：

(2*1) + (2*1) + (4*1) + (5*1) + (7*1) + (4*1) + (1*1) = 2+0+2+4+5+6+7+0+4+1 = 31

這是各位數字之和，等於 31。由於剩餘部分不能被 3 整除，所以整個數字也不能被 3 整除。

這條規則同樣可以用來判斷一個數是否能被9整除。如果一個數的各位數字和能被9整除，那麼這個數也能被9整除。反之亦然，如果一個數的各位數字之和不能被9整除，那麼這個數也不能被9整除。

邏輯謎題解答

我們將 3 必須位於 D 規則的對面這條規則稱為「D-3」規則。

• 很明顯，我們必須翻開D牌，以確保另一面是3。
• K 卡的背面必須有數字。由於對手不可能有 D，所以這張牌並不能幫助我們反駁 D-3 規則被遵守的事實。
• 卡片背面必須有一個字母。如果這個字母是 D，則符合 D-3 規則。如果背面是其他字母，對我們沒有幫助。因此，這張卡片要麼符合 D-3 規則，要麼無關緊要。無論如何，我們正在尋找一張違反該規則的卡片，以使 D-3 規則失效。背面的任何字母都無法推翻 D-3 規則，因此無需檢查。
• 7號牌的另一面必須有一個字母。如果這個字母是D，那麼這張牌就推翻了D-3規則。因此，必須檢查它是否為D-7牌，因為D-7牌與D-3規則相矛盾。

因此，只有 D 和 7 這兩張牌需要檢查。