折疊矩形拼圖
在本期通訊中,我展示了門薩公報 11 月號中的一道數學謎題。
假設有一個 1x4 的矩形。現在,將它折起來,使對角線重疊,如下圖所示。
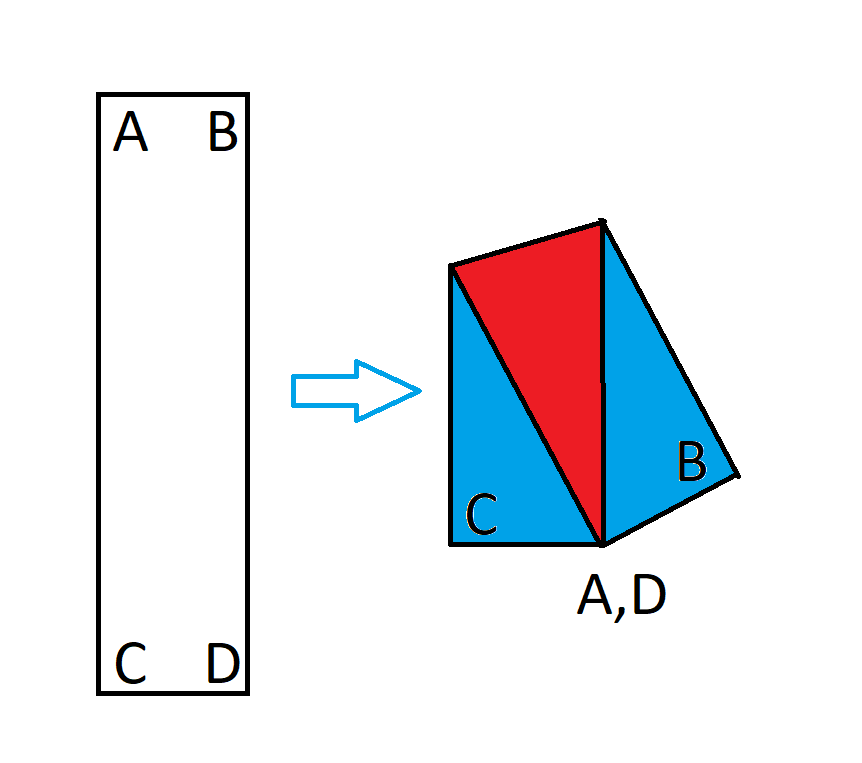
矩形折疊後,形成一個不規則的五邊形。五邊形與紙張重疊的部分與總面積的比值是多少?換句話說,就是上圖紅色區域與總面積的比值。
向下滾動查看答案和解決方案。
回答
答案是 17/47 = 約 0.3617
解決方案
為了解釋這個解,我先定義幾個點,如下圖。 F 是 E 和 G 的中點。
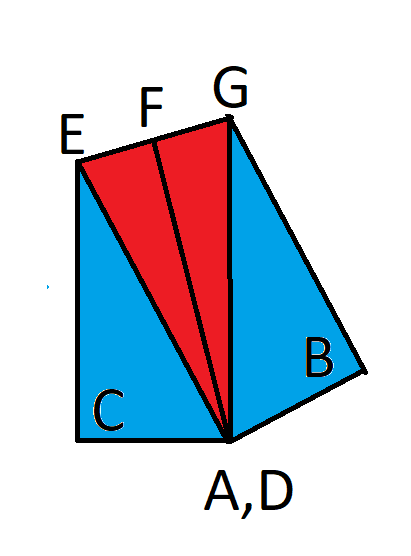
我們知道:
交流電=1
CE + AE = 4
讓我們使用勾股定理來求解 AE:
1 2 + (CE) 2 = (AE) 2
以 4 – CE 代替 AE 可得:
1 2 + (CE) 2 = (4 – CE) 2
1 + (CE) 2 = 16 – 8(CE) + (CE) 2
8(CE) = 15
CE = 15/8
回到 1 2 + (CE) 2 = (AE) 2 ,由於我們知道 EC,我們可以解出 (AE):
(AE) 2 = (CE) 2 + 1 2
(AE) 2 = (15/8) 2 + 1 2
(AE) 2 = 225/64 + 64/64
(AE) 2 = 289/64
6;字體系列:'Open Sans',sans-serif;顏色:#313131!重要">AE = 17/8折疊前,A 到 D 的長是長方形的對角線。再次使用勾股定理,長度為 sqrt(17)。
(AF) 是該長度的一半,或 sqrt(17)/2。
知道了 AE 和 AF,我們可以再用勾股定理來解 EF:
(AE) 2 = (EF) 2 + (AF) 2
(17/8) 2 = (EF) 2 + (sqrt(17)/2) 2
289/64 = (EF) 2 + 17/4
289/64 = (EF) 2 + 272/64
(EF) 2 = 17/64
EF = sqrt(17)/8
如前所述,F 是 E 和 G 的中點。因此 EG = 2*sqrt(17)/8 = sqrt(17)/4。
紅色三角形,AEG = (1/2) × 底 × 高 =
= (1/2) × sqrt(17/4) × sqrt(17)/2
= (1/2) × (17/8) = 17/16
三角形 ACE 的面積 = (1/2)*底*高 =
(1/2)×1×(15/8)=15/16。
整個五邊形的面積 = AEG + 2*ACE =
(17/16)+ 2*(15/16)= 47/16
因此,紅色區域佔整個五邊形的面積=
(17/16)/(47/16)= 17/47 = 約 0.3617


