在這一頁
德州槍戰
簡介
德州槍戰 (Texas Shootout) 是一款由Galaxy Gaming開發的簡單撲克遊戲。玩家和莊家互相對抗,牌力較大的一方獲勝。唯一的決定是從四張牌中選擇哪兩張開始。玩家的優勢在於選擇自由以及分牌的能力。莊家的優勢在於平手時獲勝。如果您正在尋找一款易於上手、波動性低且賭場優勢較大的撲克遊戲,那麼您可能會喜歡德州槍戰。
規則
- 遊戲使用六副52張的普通撲克牌進行。所有牌局均依照傳統撲克規則計分。
- 玩家進行撲克賭注加上可選的邊注。
- 莊家和閒家各發四張牌,牌面向下。玩家可以檢查自己的牌。
- 玩家可以選擇 (A) 從他的四張牌中任意選擇兩張並棄掉另外兩張,或 (B) 將手牌分成兩手,每手兩張。如果玩家選擇分牌,則必須跟注撲克牌下的注額以及附加註(如有)。
- 荷官應翻開自己的牌,並依照下面的莊家方式選擇兩張牌作為起始牌,丟棄另外兩張牌。
- 發牌人應發五張公共牌。
- 玩家和發牌人均應使用五張公共牌和兩張底牌中的任意五張牌組成最佳的五張牌撲克牌型。
- 如果玩家的牌型較大,則玩家將贏得等額的獎金。如果莊家的牌型較大,或出現平局,則莊家獲勝。
- 邊注的賠付將根據玩家五張牌的牌點數以及下方賠償表之一進行。我認為賠付表2是最常用的。此外,還有一個“羨慕獎金”,根據牌桌上所有其他玩家的牌點數計算,如下所示。
荷官將出以下列表中最大的兩張牌。如果出現兩手相同點數的牌,則荷官將會出單張點數較高的牌。每條規則均附有牌局範例。
- 一對 8 或更高。 Q
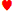 ,問
,問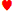
- 高牌是A ,低牌是 J 或更高。
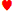 ,問
,問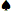
- 任何同花的 2 到 7。6
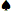 ,6
,6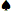
- 任何非同花的 2 到 7。6
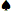 , 6
, 6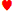
- 高 A 且同花色。 A
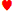 , 4
, 4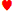
- 兩張牌均為 10 或更高且同花色。 K
 , 10
, 10
- 兩張牌均為10或更高,且不同花色。 K
 ,10
,10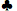
- 不同花色的高牌A。 A
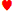 ,4
,4
- 人頭牌高花色。 J
 ,7
,7
- 人頭牌高,非同花。 J
 , 7
, 7
- 連牌同花。 4
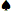 ,5
,5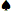
- 相連的牌,不適合。 6
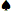 , 7
, 7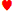
- 兩張同花色的最高牌。 8
 ,3
,3
- 兩張不同花色的最高牌。 9
 , 7動圖">
, 7動圖">
邊注賠償表
| 手 | 支付表 1 | 支付表 2 | 支付表 3 |
|---|---|---|---|
| 五張同花色的 | 5000比1 | 1000比1 | 1000比1 |
| 皇家同花順 | 500比1 | 200比1 | 200比1 |
| 同花順 | 100比1 | 75比1 | 75比1 |
| 五張相同的牌 | 50比1 | 40比1 | 40比1 |
| 四條 | 5比1 | 7比1 | 7比1 |
| 客滿 | 3比1 | 3比1 | 3比1 |
| 沖洗 | 2比1 | 2比1 | 2比1 |
| 直的 | 1比1 | 1比1 | 2比1 |
| 三條 | 失去 | 推 | 推 |
羨慕獎金
| 手 | 支付 |
|---|---|
| 五張同花色的 | 1000美元 |
| 皇家同花順 | 250美元 |
| 同花順 | 50美元 |
| 五張相同的牌 | 10美元 |
策略
以下策略不一定是最佳策略。可能會出現罰牌的情況,稍微提升玩家的勝算。
玩家應該打出下表中最大的兩張牌。如果剩餘兩張牌的預期值大於零(即26點或更高),則玩家應該分牌並繼續打出。此清單中的預期值僅為粗略估計,僅用於表示牌局順序。下表假設玩家未進行邊注。如果玩家進行了邊注,策略確實會改變。
兩張牌的排序
| 秩 | 手 | 預期價值 |
|---|---|---|
| 1 | 同花 A | 0.575301 |
| 2 | 非同花 A | 0.553041 |
| 3 | 同花 K | 0.490895 |
| 4 | 非同花 K | 0.464249 |
| 5 | 同花Q | 0.417272 |
| 6 | 不合身的Q | 0.386637 |
| 7 | 同花 J | 0.345383 |
| 8 | 非同花J | 0.311134 |
| 9 | 同花 10 | 0.275898 |
| 10 | 非同花10 | 0.237068 |
| 11 | 同花9 | 0.205034 |
| 12 | 非同花9 | 0.162011 |
| 十三 | 同花 8 | 0.154705 |
| 14 | 同花 A,K | 0.109348 |
| 15 | 非同花的 8 | 0.107616 |
| 16 | 同花 7 | 0.106813 |
| 17 | 同花 A,Q | 0.069761 |
| 18 | 同花 6 | 0.05977 |
| 19 | 非同花色的 7 | 0.055731 |
| 20 | 非同花色 A,K | 0.053211 |
| 21 | 同花 A,J | 0.033959 |
| 22 | 同花 5 | 0.013691 |
| 23 | 同花 K,Q | 0.012594 |
| 24 | 同花 A,10 | 0.011557 |
| 二十五 | 不合身的 A,Q | 0.010262 |
| 二十六 | 非同花的 6 | 0.005561 |
| 二十七 | 同花 K,J | -0.0187 |
| 二十八 | 非同花 A,J | -0.029408 |
| 二十九 | 同花 4 | -0.033235 |
| 三十 | 同花 A,9 | -0.039459 |
| 31 | 非同花5 | -0.04346 |
| 三十二 | 同花 K,10 | -0.044542 |
| 33 | 非同花色的K,Q | -0.048566 |
| 三十四 | 非同花 A,10 | -0.053852 |
| 三十五 | 同花 A,8 | -0.060539 |
| 三十六 | 同花Q,J | -0.063067 |
| 三十七 | 同花 3 | -0.078173 |
| 三十八 | 同花 A,7 | -0.0806 |
| 三十九 | 非同花 K,J | -0.082504 |
| 40 | 同花Q,10 | -0.088102 |
| 41 | 同花 K,9 | -0.089785 |
| 四十二 | 非同花4 | -0.093836 |
| 43 | 同花 A,6 | -0.100855 |
| 四十四 | 同花 A,5 | -0.10132 |
| 45 | 非同花 A,9 | -0.110164 |
| 46 | 非同花 K,10 | -0.11166 |
| 四十七 | 同花 A,4 | -0.116193 |
| 四十八 | 同花 J,10 | -0.122052 |
| 49 | 同花 2 | -0.122698 |
| 50 | 同花 K,8 | -0.124103 |
| 51 | 非同花Q,J | -0.127974 |
| 52 | 同花Q,9 | -0.12845 |
| 53 | 同花 A,3 | -0.131083 |
| 54 | 非同花 A,8 | -0。131953 |
| 55 | 同花 K,7 | -0.139746 |
| 56 | 非同花3 | -0.142697 |
| 57 | 同花 A,2 | -0.145134 |
| 58 | 非同花 A,7 | -0.154346 |
| 59 | 非同花Q,10 | -0.155267 |
| 60 | 同花 K,6 | -0.15593 |
| 61 | 同花 J,9 | -0.159122 |
| 62 | 非同花 K,9 | -0.160559 |
| 63 | 同花Q,8 | -0.161784 |
| 64 | 同花 K,5 | -0.170875 |
| 65 | 非同花 A,6 | -0.176551 |
| 66 | 非同花 A,5 | -0.17671 |
| 67 | 同花 10,9 | -0.180637 |
| 68 | 同花 K,4 | -0.185425 |
| 69 | 非同花 J,10 | -0.189734 |
| 70 | 不合身的 2 | -0.191214 |
| 71 | 同花 J,8 | -0.191644 |
| 72 | 非同花 A,4 | -0.193476 |
| 73 | 同花Q,7 | -0.194186 |
| 74 | 非同花 K,8 | -0.197604 |
| 75 | 同花 K,3 | -0.199133 |
| 76 | 非同花Q,9 | -0.199229 |
| 77 | 同花Q,6 | -0.206405 |
| 78 | 非同花 A,3 | -0.209351 |
| 79 | 同花 10,8 | -0.2107 |
| 80 | 同花 K,2 | -0.213633 |
| 81 | 非同花 K,7 | -0.214514 |
| 82 | 同花9,8 | -0.217352 |
| 83 | 同花Q,5 | -0.220169 |
| 84 | 同花 J,7 | -0.223077 |
| 85 | 非同花 A,2 | -0.22489 |
| 86 | 非同花 J,9 | -0.22991 |
| 87 | 非同花 K,6 | -0.232094 |
| 88 | 同花Q,4 | -0.235311 |
| 89 | 非同花Q,8 | -0.235583 |
| 90 | 同花 9,7 | -0.240067 |
| 91 | 同花 10,7 | -0.240998 |
| 92 | 同花 8,7 | -0.24438 |
| 93 | 非同花 K,5 | -0.248762 |
| 94 | 同花Q,3 | -0.249074 |
| 95 | 非同花 10,9 | -0.251406 |
| 96 | 同花 J,6 | -0.252745 |
| 97 | 同花Q,2 | -0.262805 |
| 98 | 同花 J,5 | -0.263285 |
| 99 | 非同花 K,4 | -0.264611 |
| 100 | 非同花 J,8 | -0.265759 |
| 101 | 同花 8,6 | -0.266064 |
| 102 | 同花 9,6 | -0.266234 |
| 103 | 同花 7,6 | -0.268436 |
| 104 | 同花 10,6 | -0.270272 |
| 105 | 非同花Q,7 | -0.270629 |
| 106 | 同花 J,4 | -0.27729 |
| 107 | 非同花 K,3 | -0.279442 |
| 108 | 非同花Q,6 | -0.283973 |
| 109 | 非同花 10,8 | -0.284135 |
| 110 | 非同花9,8 | -0.290229 |
| 111 | 同花 J,3 | -0.290602 |
| 112 | 同花 7,5 | -0.291758 |
| 113 | 同花 6,5 | -0.292394 |
| 114 | 同花 9,5 | -0.29242 |
| 115 | 同花 8,5 | -0.292459 |
| 116 | 非同花 K,2 | -0.295417 |
| 117 | 同花 10,5 | -0.298923 |
| 118 | 非同花Q,5 | -0.29957 |
| 119 | 非同花 J,7 | -0.299933 |
| 120 | 同花 J,2 | -0.304647 |
| 121 | 同花 10,4 | -0.309336 |
| 122 | 同花 5,4 | -0。314195 |
| 123 | 非同花9,7 | -0.315221 |
| 124 | 非同花Q,4 | -0.315476 |
| 125 | 非同花 10,7 | -0.317375 |
| 126 | 同花 6,4 | -0.318104 |
| 127 | 非同花 8,7 | -0.318633 |
| 128 | 同花 7,4 | -0.3204 |
| 129 | 同花 8,4 | -0.321035 |
| 130 | 同花9,4 | -0.321037 |
| 131 | 同花 10,3 | -0.322631 |
| 132 | 同花9,3 | -0.329597 |
| 133 | 非同花Q,3 | -0.33053 |
| 134 | 非同花 J,6 | -0.331918 |
| 135 | 同花 10,2 | -0.335747 |
| 136 | 同花 5,3 | -0.340684 |
| 137 | 同花 9,2 | -0.342481 |
| 138 | 非同花9,6 | -0.342769 |
| 139 | 非同花 8,6 | -0.34313 |
| 140 | 非同花 J,5 | -0.343243 |
| 141 | 非同花7,6 | -0.34495 |
| 142 | 非同花Q,2 | -0.346033 |
| 143 | 同花 6,3 | -0.347068 |
| 144 | 非同花 10,6 | -0.348636 |
| 145 | 同花 7,3 | -0.348941 |
| 146 | 同花 8,3 | -0.349902 |
| 147 | 非同花 J,4 | -0.358831 |
| 148 | 同花 4,3 | -0.358841 |
| 149 | 同花 8,2 | -0.359102 |
| 150 | 同花 5,2 | -0.369618 |
| 151 | 非同花 7,5 | -0.370327 |
| 152 | 非同花 6,5 | -0.370589 |
| 153 | 非同花 9,5 | -0.371722 |
| 154 | 非同花 8,5 | -0.371759 |
| 155 | 非同花 J,3 | -0.373192 |
| 156 | 同花 6,2 | -0.376459 |
| 157 | 同花 7,2 | -0.377908 |
| 158 | 非同花 10,5 | -0.37939 |
| 159 | 同花 4,2 | -0.384973 |
| 160 | 非同花 J,2 | -0.388862 |
| 161 | 非同花 10,4 | -0.390903 |
| 162 | 非同花 5,4 | -0.39378 |
| 163 | 非同花6,4 | -0.398771 |
| 164 | 非同花7,4 | -0.401385 |
| 165 | 同花 3,2 | -0.401451 |
| 166 | 非同花9,4 | -0.402623 |
| 167 | 非同花 8,4 | -0.402719 |
| 168 | 非同花 10,3 | -0.40569 |
| 169 | 非同花9,3 | -0.412853 |
| 170 | 非同花 10,2 | -0.420634 |
| 171 | 非同花 5,3 | -0.422846 |
| 172 | 非同花9,2 | -0.427508 |
| 173 | 非同花 6,3 | -0.430175 |
| 174 | 非同花7,3 | -0.432623 |
| 175 | 非同花 8,3 | -0.433916 |
| 176 | 非同花 4,3 | -0.442055 |
| 177 | 非同花 8,2 | -0.444371 |
| 178 | 非同花 5,2 | -0.454349 |
| 179 | 非同花 6,2 | -0.462125 |
| 180 | 非同花7,2 | -0.464479 |
| 181 | 非同花 4,2 | -0.470729 |
| 182 | 非同花3,2 | -0.488024 |
分析
每手初始牌有五種可能的結果。大多數情況下,玩家會贏或輸一個單位。如果玩家分牌,他可能贏兩個單位、平手或輸兩個單位。下表顯示了每手初始牌所有可能淨贏的機率和回報。右下角單元格顯示莊家優勢為 2.57%。
撲克賭注回報表
| 贏 | 可能性 | 返回 |
|---|---|---|
| 2 | 0.026618 | 0.053236 |
| 1 | 0.437762 | 0.437762 |
| 0 | 0.032391 | 0 |
| -1 | 0.489783 | -0.489783 |
| -2 | 0.013445 | -0.026891 |
| 全部的 | 1 | -0.025675 |
玩家分牌的機率為7.25%。因此風險因子為2.57%/1.0725 = 2.39%。
接下來的三個回報表是在考慮嫉妒獎金之前,邊注的三種可能賠償表。表中的機率假設玩家遵循上述策略,該策略是為只進行撲克下注的玩家設計的。如果玩家進行了邊注,那麼透過進行我不知道的策略調整,他可能會以犧牲撲克下注為代價,從邊注中獲得更多價值。然而,根據我的專業意見,這種策略調整的效益微乎其微。除非是在使用賠付表3的滿桌玩家遊戲中,否則我建議不要進行邊注。
邊注賠償表 1
| 手 | 支付 | 可能性 | 返回 |
|---|---|---|---|
| 五張同花色的 | 5000比1 | 0.000001 | 0.004175 |
| 皇家同花順 | 500比1 | 0.000082 | 0.040866 |
| 同花順 | 100比1 | 0.000203 | 0.020345 |
| 五張相同的牌 | 50比1 | 0.001213 | 0.060651 |
| 四條 | 5比1 | 0.020021 | 0.100103 |
| 客滿 | 3比1 | 0.084969 | 0.254907 |
| 沖洗 | 2比1 | 0.050618 | 0.101237 |
| 直的 | 1比1 | 0.031316 | 0.031316 |
| 三條 | -1 到 1 | 0.098834 | -0.098834 |
| 所有其他 | -1 到 1 | 0.712743 | -0.712743 |
| 全部的 | 1 | -0.197977 |
邊注賠償表 2
| 手 | 支付 | 可能性 | 返回 |
|---|---|---|---|
| 五張同花色的 | 1000比1 | 0.000001 | 0.000835 |
| 皇家同花順 | 200比1 | 0.000082 | 0.016346 |
| 同花順 | 75比1 | 0.000203 | 0.015259 |
| 五張相同的牌 | 40比1 | 0.001213 | 0.04852 |
| 四條 | 7比1 | 0.020021 | 0.140145 |
| 客滿 | 3比1 | 0.084969 | 0.254907 |
| 沖洗 | 2比1 | 0.050618 | 0.101237 |
| 直的 | 1比1 | 0.031316 | 0.031316 |
| 三條 | 推 | 0.098834 | 0 |
| 所有其他 | -1 到 1 | 0.712743 | -0.712743 |
| 全部的 | 1 | -0.104177 |
邊注賠償表 3
| 手 | 支付 | 可能性 | 返回 |
|---|---|---|---|
| 五張同花色的 | 1000比1 | 0.000001 | 0.000835 |
| 皇家同花順 | 200比1 | 0.000082 | 0.016346 |
| 同花順 | 75比1 | 0.000203 | 0.015259 |
| 五張相同的牌 | 40比1 | 0.001213 | 0.04852 |
| 四條 | 7比1 | 0.020021 | 0.140145 |
| 客滿 | 3比1 | 0.084969 | 0.254907 |
| 沖洗 | 2比1 | 0.050618 | 0.101237 |
| 直的 | 2比1 | 0.031316 | 0.062632 |
| 三條 | 推 | 0.098834 | 0 |
| 所有其他 | -1 到 1 | 0.712743 | -0.712743 |
| 全部的 | 1 | -0.072861 |
最終表格顯示了計入「羨慕獎金」後的邊注賭場優勢。左欄顯示玩家人數(包括您自己),上方顯示邊注賠償表。該表格假設邊注金額為 5 美元。隨著邊注金額的增加,「羨慕獎金」的相對價值會下降。
帶有羨慕獎金的邊注莊家優勢
| 數量 玩家 | 支付表 1 | 支付表 2 | 支付表 3 |
|---|---|---|---|
| 7 | 14.57% | 5.19% | 2.06% |
| 6 | 15.44% | 6.06% | 2.93% |
| 5 | 16.31% | 6.93% | 3.80% |
| 4 | 17.18% | 7.80% | 4.67% |
| 3 | 18.05% | 8.67% | 5.54% |
| 2 | 18.93% | 9.55% | 6.41% |
| 1 | 19.80% | 10.42% | 7.29% |
方法論
我喜歡盡可能地用直接的組合分析法來分析遊戲。然而,這款遊戲中可能的組合數高達 2,980,936,261,442,170,000,000,000,000,000。即使有最好的捷徑,一台計算機要完美地分析所有組合,也可能需要數月甚至數年的時間。因此,對於這款遊戲,隨機模擬顯然是合適的。隨機模擬的一個好處是,分析師必須量化程式要遵循的策略,而不是像暴力破解程式那樣,它可以即時找出正確的策略,但在牌局結束後很快就會忘記。我想出來的就是兩張牌手牌排名策略。如上所述,它可能並不完美,但如果我要找出懲罰牌例外,那麼世界上可能學習它們的人為零。任何具有這種追求完美遊戲精神的人可能會玩二十一點或視訊撲克,因為玩家可以在其中佔據優勢。


