在這一頁
基諾霹靂
簡介
基諾爆炸 (Keno Explosion) 是 IGT 推出的基諾遊戲。玩家需要將炸彈放在三個未選的數字上。如果抽出的球與炸彈對應的數字匹配,炸彈就會爆炸;如果炸彈碎片擊中玩家選擇的數字,則算中獎。
規則
- 玩家須從1至80中選出2至10個數字。
- 遊戲將隨機選取三個玩家未選擇的數字,並用炸彈標記它們。
- 遊戲將從 1 到 80 中不重複地抽取 20 個數字。
- 如果遊戲中抽取的任何球與玩家選擇的數字相匹配,則應算作「接球」。
- 如果遊戲抽出的球與炸彈標記的三個數字之一匹配,則該炸彈將爆炸。爆炸後,一至三個碎片將落在遊戲未選中或未標記的57個數字中的一個上。
- 任何數字都不能被兩個或更多的碎片擊中。
- 如果炸彈碎片落在玩家所選的數字上,也應算作一次「接住」。
- 根據 27 枚炸彈的小樣本分析,每枚炸彈的平均碎片數量為 1.85 個。
- 球員將根據接球次數和公佈的賠付表獲得報酬。
- 下面的賠付表只是一個例子,它是在拉斯維加斯紅岩賭場以 10¢ 的賭注看到的。
如果您對這些規則不清楚,以下是規則截圖。點擊任一圖片可看大圖。
 | 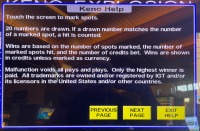 |
下表顯示了賠付表示例。請注意,許多賠償金以 0.5 結尾。為了讓賠付總額保持整數,玩家必須下注偶數個硬幣。
基諾爆炸賠率表
| 抓住 | 選擇 2 | 選擇 3 | 選擇 4 | 選擇 5 | 挑選 6 | 選擇 7 | 選8 | 選9 | 挑選 10 |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | 12 | 2 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 3 | 32.5 | 3.5 | 2 | 1.5 | 0.5 | 0 | 0 | 0 | |
| 4 | 107 | 12.5 | 4 | 1.5 | 1 | 0.5 | 0 | ||
| 5 | 450 | 53 | 十三 | 7 | 3 | 2.5 | |||
| 6 | 1000 | 217 | 54 | 23 | 12 | ||||
| 7 | 3750 | 835 | 171 | 77 | |||||
| 8 | 5000 | 2400 | 505 | ||||||
| 9 | 5000 | 2300 | |||||||
| 10 | 5000 |
例子
下圖是我在遊戲中選了六個號碼——44、45、46、54、55 和 56。炸彈分別放在 1、36 和 41 號。這張照片拍攝於開獎後,炸彈爆炸前。請注意,在炸彈爆炸前,我選了六個號碼中的四個,中獎金額為 8。
上圖是在炸彈爆炸後拍攝的。炸彈碎片擊中了21、38、55和77。這些數字的背景是紅色的,看起來像是著火了一樣,所以很容易辨認。之前被炸彈佔據的數字1、36和41看起來已經破碎。其中一個碎片擊中了55,而這正是我選擇的號碼之一。這使我的中獎次數從4次增加到5次,中獎次數也從8次增加到106次。
炸彈會被炸毀嗎?
下表顯示了遊戲在20個球的抽籤中,抓到0到3個炸彈的機率,假設任一個炸彈與抽籤球相符的機率為20/80 = 25%。請注意,三個炸彈都與抽籤球相符的機率為0.013875。
預計炸彈爆炸
| 炸彈 漁獲量 | 組合 | 可能性 |
|---|---|---|
| 3 | 1140 | 0.013875 |
| 2 | 11400 | 0.138754 |
| 1 | 35400 | 0.430867 |
| 0 | 34220 | 0.416504 |
| 全部的 | 82160 | 1.000000 |
下表顯示了在208場比賽的小樣本中,比賽平局時投下的炸彈數量。右列顯示了在208場比賽中,給定投擲炸彈次數的預期場次。
炸彈捕獲採樣
| 炸彈 漁獲量 | 樣本 觀察 | 預期的 |
|---|---|---|
| 3 | 三十 | 2.89 |
| 2 | 三十四 | 28.86 |
| 1 | 二十五 | 89.62 |
| 0 | 119 | 86.63 |
| 全部的 | 208 | 208.00 |
請注意,在208場比賽中,有30場比賽導致三枚炸彈全部爆炸。如果比賽遵循自然機率,那麼三枚炸彈全部爆炸的預期場次將是2.89。
在 208 場比賽中,發生 30 枚或更多炸彈爆炸的機率與預期值相差 17.78 個標準差。發生 30 枚或更多炸彈爆炸的機率為20,840,430,698,432,300,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000
對上述觀察結果及預期進行卡方檢驗,結果出現偏斜的機率為12,703,492,578,520,200,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000
值得注意的是,第一個規則畫面上顯示:「爆炸和碎片是在抽出所有數字後進行評估的。」雖然這條規則有多種解釋,但它在我看來意味著炸彈發生的一切都是獨立決定的,而不一定是由隨機抽取的球決定的。
我想強調的是,如果這款遊戲出現失誤,那也算是對玩家有利的失誤。然而,我認為任何一方的失誤都違反了內華達州修訂法令 14.040.5 ,該法令規定: “對於代表真人賭博遊戲的遊戲設備,某個符號或其他元素在遊戲結果中出現的數學概率必須等於該符號或元素在真人賭博遊戲中出現的數學概率。 ”
對遊戲進行隨機模擬,假設各方面都採用自然賠率,結果顯示回報率為 82.49%。據我所知,該遊戲的開發商 IGT 只允許將賠率設定到 85%。在紅岩賭場的同一台機器上,其他 5 美分基諾遊戲的平均回報率為 89.45%。這進一步證明遊戲有缺陷,因此與自然抽獎(每個號碼的抽獎機率均等)相比,抽獎過程中的球更有可能中炸彈。
影片
在此影片中,我提供了證據和論據,說明為什麼基諾爆炸不符合現場基諾的自然機率。




