在這一頁
不同的雙打
簡介
「不同雙倍」是比洛克西博里瓦奇賭場常見的一種擲骰子附加賭注。它根據擲骰者在擲出總數為7之前擲出的不同雙倍的次數來支付賠付。賠付表如下:
- 6 次雙倍賠率為 100 比 1
- 5 次雙倍賠率為 15 比 1
- 4 個雙倍賠率為 8 比 1
- 3 次雙倍賠率為 4 比 1
分析
下表顯示了所有可能結果的機率及其對回報的貢獻。右下角單元格顯示莊家優勢為 27.92%(哎喲!)。
不同雙打回報表
| 雙打 | 支付 | 組合 | 可能性 | 返回 |
|---|---|---|---|---|
| 6 | 100 | 1 | 0.001082 | 0.108225 |
| 5 | 15 | 6 | 0.006494 | 0.097403 |
| 4 | 8 | 21 | 0.022727 | 0.181818 |
| 3 | 4 | 56 | 0.060606 | 0.242424 |
| 2 | -1 | 126 | 0.136364 | -0.136364 |
| 1 | -1 | 252 | 0.272727 | -0.272727 |
| 0 | -1 | 462 | 0.500000 | -0.500000 |
| 全部的 | 924 | 1.000000 | -0.279221 |
代數分析
任何給定雙倍的機率為 1/36。因此,任何雙倍的機率為 6/36 = 1/6。任何七的機率為 1/6。除了雙倍和七之外,我們可以忽略所有擲出的點數。因此,假設有一輪擲出的點數與投注相關,則該輪的機率如下:
- 任一雙倍 = 1/2
- 任七 = 1/2
第一次擲出有效點數 7 的機率是 1/2。因此,出現雙倍點數的機率為零。
否則,玩家就會擲出雙點。現在我們可以忽略再次擲出雙點這一重要事件。兩種重要事件的機率現在分別為:
- 任何顯著的雙倍 = 5/11
- 任七 = 6/11
此時,玩家擲出7點(一次雙倍)的機率為6/11。因此,擲出一次雙倍的總體機率為(1/2)*(6/11) = 3/11 = 約27.27%。
否則,玩家就會擲出第二個雙倍。現在,我們可以忽略擲出兩個不同的雙倍作為顯著事件。現在,兩種顯著事件的機率分別為:
- 任何顯著的雙倍 = 4/10
- 任七 = 6/10
此時玩家擲出兩次雙倍點數的機率為 6/10。因此,一次雙倍點數的總體機率為 (1/2)*(5/11)*(6/10) = 3/22 = 約 13.6363636%。
否則,玩家就會擲出第三個雙數。現在我們可以忽略擲出三個不同的雙數作為顯著事件。兩種顯著事件的機率現在分別為:
- 任何顯著的雙倍 = 3/9
- 任七 = 6/9
此時玩家擲出兩次雙倍點數的機率為 6/9。因此,擲出一次雙倍點數的總體機率為 (1/2)*(5/11)*(4/10)*(6/9) = 2/33 = 約 6.060606%。
否則,玩家就會擲出第四個雙數。現在我們可以忽略擲出四個不同的雙數作為顯著事件。兩種顯著事件的機率現在分別為:
- 任何顯著的雙倍 = 2/8
- 任七 = 6/8
此時玩家擲出兩次雙倍點數的機率為 6/8。因此,一次雙倍點數的總體機率為 (1/2)*(5/11)*(4/10)*(3/9)*(6/8) = 1/44 = 約 2.272727%。
否則,玩家就會擲出第五個雙數。現在我們可以忽略擲出五個不同的雙數作為顯著事件。兩種顯著事件的機率現在分別為:
- 任何顯著的倍數 = 1/7
- 任七 = 6/7
此時玩家擲出兩次雙倍的機率為 6/7。因此,一次雙倍的總體機率為 (1/2)*(5/11)*(4/10)*(3/9)*(2/8)*(6/7) = 1/154 = 約 0.649351%。
否則,玩家會擲出最後一個剩下的雙點。其機率為 (1/2)*(5/11)*(4/10)*(3/9)*(2/8)*(1/7) = 1/924 = 約 0.108225%。
現在,我們可以將所有這些放在上面的回報表中。組合數共有 924 種。
積分分析
想像一下,重大事件不再由一次擲骰子來決定,而是被視為一個時間瞬間。假設事件之間的時間間隔具有無記憶性,平均間隔一個單位時間。換句話說,事件之間的時間間隔服從平均值為1的指數分佈。這對裁決賭注來說無關緊要,因為事件仍然是一次一個地發生的。
特定雙倍事件之間的時間間隔服從指數分佈,平均值為 12。之所以使用 12,是因為如果發生重大事件,則有 1/12 的機率是該特定雙倍事件。因此,特定雙倍事件在 x 個單位時間內未發生的機率為 exp(-x/12)。因此,它發生的機率為 1-exp(-x/12)。
設 x 為投注開始以來的時間單位數。所有雙倍出現且七點未出現的機率為 (1-exp(-x/12)) 6 × exp(-x/2)。
以在時間 x 擲出 7 來結束此過程,將其乘以 1/2(擲出 7 的機率),得到在時間 x 恰好擲出獲勝的機率為 (1/2) ×(1-exp(-x/12)) 6 × exp(-x/2)
若要找出所有時間內獲勝的機率,請從 1 到無限大進行積分:
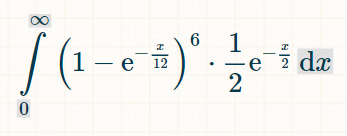
為了求積分,我推薦使用這個積分計算器。在積分欄中輸入「(1-exp(-x/12))^6*(1/2)*exp(-x/2)」。對於積分極限,在選項下輸入 0 和 ∞。然後點選“開始”。「它將給出下面的積分:
(-(1-e^(-x/12))^12+(60*(1-e^(-x/12))^11)/11-12*(1-e^(-x/12))^10+(40 *(1-e^(-x/12))^9)/3-(15*(1-e^(-x/12))^8)/2+(12*(1-e^(-x/12))^7)/7)/2
但是,我們不需要輸入 0。計算器給的答案是 1/924 = 約 0.001082251082251082。
這是五種不同加倍的積分。結果為 6 是因為有 6 種可能的加倍沒有被算出來:
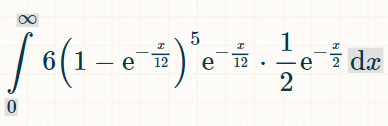
這是在 x 個時間單位內獲勝的機率:
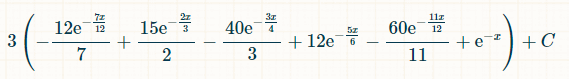
將積分範圍設為從 0 到無限大,則擲出五個不同雙數的機率為 1/154。
這是四個不同雙精度浮點數的積分。之所以是 15,是因為在 6 個浮點數中,有 4 個浮點數有 6!/(4!*2!) = 15 種可能的組合:
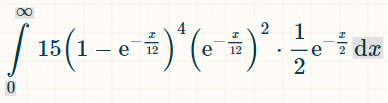
這是在 x 個時間單位內獲勝的機率:
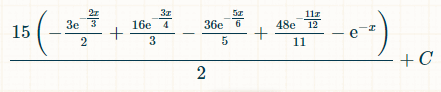
將積分範圍設為從 0 到無限大,則擲出四個不同雙精度數的機率為 1/44。
這是三個不同雙精度數的積分。之所以是 20,是因為在 6 個雙精度數中,有 3 個可能的組合,總共有 6!/(3!*3!) = 20 種:
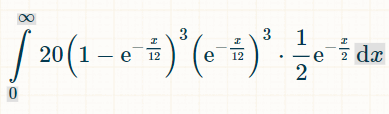
這是在 x 個時間單位內獲勝的機率:
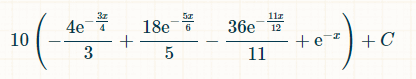
將積分範圍設為從 0 到無限大,則擲出三個不同雙精度數的機率為 2/33。



