在這一頁
紅利擲骰子
簡介
獎金擲骰子(Bonus Craps)是擲骰子遊戲中的一組三種附加賭注。具體如下:
- 小-如果投擲者擲出總數為 2 至 6 之間的所有點數,然後才擲出總數為 7,則獲勝。獲勝賠率通常為 30 比 1。
- 高點數 (Tall) — 若投擲者擲出總數為 8 至 12 之間的所有點數,然後才擲出總數為 7,則獲勝。獲勝賠率通常為 30 比 1。
- 全部 — 如果投擲者在擲出總數 7 之前擲出 2 到 12 之間的所有數字(除 7 外),則獲勝。獲勝賠率通常為 150 比 1。
2021 年,我開始在威尼斯人看到這種名為「Diceology」的賭注。
分析
下表顯示了我對小注和大注的分析,獲勝賠率為 30 比 1。右下角單元格顯示莊家優勢為 18.30%。
小而高
| 事件 | 支付 | 可能性 | 返回 |
|---|---|---|---|
| 贏 | 三十 | 0.026354 | 0.790617 |
| 損失 | -1 | 0.973646 | -0.973646 |
| 全部的 | 1.000000 | -0.183029 |
過去,有些賭桌在小型和大型賭桌上的賠率高達1比34。如今這些賠率更高,賭場優勢高達7.76%。
下表顯示了我對「全部下注」的分析,獲勝賠率為 150 比 1。右下角單元格顯示莊家優勢為 20.61%。
全部
| 事件 | 支付 | 可能性 | 返回 |
|---|---|---|---|
| 贏 | 150 | 0.005258 | 0.788655 |
| 損失 | -1 | 0.994742 | -0.994742 |
| 全部的 | 1.000000 | -0.206087 |
我見過「全注」的其他賠率,包括1比155和1比175。記得在賠率中減去1,才能將賠率從「一比一」轉換為「一比一」。下表顯示了賠率在150到175之間,且能被5整除的賠率的賭場優勢。
All Bet 的莊家優勢總結
| 支付 | 莊家優勢 |
|---|---|
| 150 | 20.61% |
| 155 | 17.98% |
| 160 | 15.35% |
| 165 | 12.72% |
| 170 | 10.09% |
| 175 | 7.46% |
方法論
我從三個方面分析了 Bonus Craps,如下所示:
- 模擬—這可能是最簡單的方法。然而,對於像我這樣的數學純粹主義者來說,模擬總是無法帶來足夠的智力滿足。
- 馬可夫鏈-這種方法繁瑣且耗時。對於「小」和「高」模型,它需要一個 6x6 的轉移矩陣,而對於「全」模型,則需要一個 12x12 的轉移矩陣。
- 積分微積分-使用積分計算器,這種方法非常簡單。我將在下文中更深入地解釋。
想像一下,重大事件不再由一次擲骰子來決定,而是被視為一個時間瞬間。假設事件之間的時間間隔具有無記憶性,平均間隔為一個時間單位。換句話說,事件之間的時間間隔服從平均值為1的指數分佈。這對於判定賭注而言無關緊要,因為事件仍然是一次一個地發生的。
以下是在 x 個時間單位內任何給定總數至少未滾動一次的機率:
- 2 或 12:exp(-x/36)
- 3 或 11:exp(-x/18)
- 4 或 10:exp(-x/12)
- 5 或 9:exp(-x/9)
- 6 或 8:exp(-5x/36)
- 7:exp(-x/6)
我們先來看看小注。大注的賠率和小注完全一樣。
在 x 個時間單位內,擲出 2、3、4、5 和 6 而未擲出 7 的機率為: (1-exp(-x/36))*(1-exp(-x/18))*(1-exp(-x/12))*(1-exp(-x/9)))*(1-exp(-x/12))*(1-exp(-x/9))*(1-exp(-x/12))*(1-exp(-x/9))*(1-exp(-x/12) 擲出時間, x/4x/4x2 7,之前擲出的總數為 2 到 6,則該玩家的機率為:
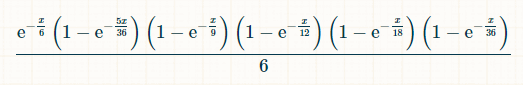
對於積分,我使用了這個積分計算器。
由於中獎號碼 7 隨時可能出現,中獎機率就是該機率對 x 從 0 到無限大的積分。我們不需要知道,但在代入積分極限之前,積分是(-6*e^(-x/6)+(36*e^(-(7*x)/36))/7+(9*e^(-(2*x)/9))/2-(36*e^ (-(11*x)/36))/11-3*e^(-x/3)-(36*e^(-(13*x)/36))/13+(18*e^(- (7*x)/18))/7+(12*e^(-(5*x)/12)/18))/7+(12*e^(-(5*x)/12)/^5(2)/ (-(19*x)/36))/19-(9*e^(-(5*x)/9))/5+(12*e^(-(7*x)/12))/7)/6。
代入積分極限,答案是 20049 / 760760 = 約 0.02635390924864609。
接下來我們來看全注。
在 x 個時間單位內,擲出 2、3、4、5、6、8、9、10、11 和 12 而未擲出 7 的機率為: (1-exp(-x/36)) 2 *(1-exp(-x/16)) 2 *(1-exp(-x/12) 22 *(-x/16)) 2 *(1-exp(-x/12) 22 *(3) *195) * 2 *exp(-x/6) 在時間 x 處,玩家擲出 7,之前擲出的總數為 2 到 6,則該玩家的機率為:
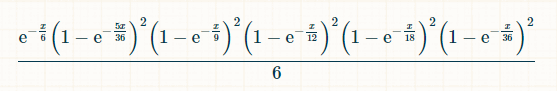
由於中獎數字 7 隨時可能出現,中獎機率就是該機率對 x 從 0 到無限大的積分。我們不需要知道這個值,但在帶入積分極限之前,積分等於(-6*e^(-x/6)+(72*e^(-(7*x)/36))/7+(9*e^(-(2*x)/9))/2-8*e^(-x/4)-(18*e^(-(5 *x)/18))/5-(72*e^(-(11*x)/36))/11+(72*e^(-(13*x)/36))/13+(108*e^(-(7*x)/1) 8))/7+(24*e^(-(5*x)/12))/5-(27*e^(-(4*x)/9))/4-(216*e^(-(17*x)/36))/17-10* e^(-x/2)-(72*e^(-(19*x)/36))/19+(27*e^(-(5*x)/9))/5+(144*e^(-(7*x)/12))/7+ (54*e^(-(11*x)/18))/11-(72*e^(-(23*x)/36))/23-(15*e^(-(2*x)/3))/2-(216*e^( -(25*x)/36))/25-(54*e^(-(13*x)/18))/13+(8*e^(-(3*x)/4))/3+(54*e^(-(7*x)/9) )/7+(72*e^(-(29*x)/36))/29-(72*e^(-(31*x)/36))/31-(9*e^(-(8*x)/9))/8-(24*e ^(-(11*x)/12))/11+(18*e^(-(17*x)/18))/17+(72*e^(-(35*x)/36))/35-e^(-x))/6。
代入積分極限,答案是 126538525259 / 24067258815600 = 0.0052577040961964420049。



