在這一頁
賓果機率:Station Casinos 巨額累積獎金分析
在這一頁
更新
自從我寫了第一份報告後,Station 的賭場顯然又改變了賠率和雙數的分配,大概是在十月份的某個時候。下表顯示了我最近拿到的牌以及另一張我暫且稱之為「L」的牌的分配情況。
 俄亥俄州 推薦的線上賓果遊戲室
俄亥俄州 推薦的線上賓果遊戲室
巨型賓果卡的新樣本
| 數位 賠率 | 麥克的樣本 | L 的樣本 | 總樣本 | 可能性 |
|---|---|---|---|---|
| 9 | 2 | 3 | 5 | 0.011261 |
| 10 | 7 | 10 | 17 | 0.038288 |
| 11 | 14 | 二十五 | 三十九 | 0.087838 |
| 12 | 三十四 | 41 | 75 | 0.168919 |
| 十三 | 41 | 71 | 112 | 0.252252 |
| 14 | 86 | 110 | 196 | 0.441441 |
| 全部的 | 184 | 260 | 444 | 1 |
雖然賠率範圍保持不變,但機率現在嚴重偏向14,而不是之前的更均勻分佈。賠率越高,贏得累積獎金就越困難。基於此樣本,如果您想要獲得正的預期值,我現在建議等到巨球達到54。
下表將我的總樣本與相同樣本大小下的預期總數進行比較,並假設採用 Stephen L. Cavallaro(Station Casinos 執行副總裁兼首席營運官)之前向我解釋的相同抽牌方法,假設每個總數的機率相同。
實際總數與預期總數
| 數位 賠率 | 樣品總計 | 預計總計 |
|---|---|---|
| 9 | 5 | 33.17 |
| 10 | 17 | 60.48 |
| 11 | 三十九 | 87.61 |
| 12 | 75 | 101.15 |
| 十三 | 112 | 93.18 |
| 14 | 196 | 68.41 |
| 全部的 | 444 | 444 |
顯而易見,我的結果與預期不符。此分佈的偏度與預期進行比較的統計檢定結果顯示,卡方統計量為 330.71,自由度為 5。出現如此或更大偏度結果的機率為402,433,741,048,496,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000換個角度來看,連續八次中強力球的機率更大。
為了進一步論證抽牌方式確實發生了變化,下表展示了我所謂的更改前後的樣本結果。樣本1採集於8月,樣本2採集於10月30日及11月1日。
舊樣本與新樣本
| 數位 賠率 | 範例 1 | 範例 2 | 樣本 1 機率 | 樣本 2 機率 |
|---|---|---|---|---|
| 9 | 三十五 | 5 | 13.51% | 1.13% |
| 10 | 三十五 | 17 | 13.51% | 3.83% |
| 11 | 三十四 | 三十九 | 13.13% | 8.78% |
| 12 | 四十八 | 75 | 18.53% | 16.89% |
| 十三 | 55 | 112 | 21.24% | 25.23% |
| 14 | 52 | 196 | 20.08% | 44.14% |
| 全部的 | 259 | 444 | 100% | 100% |
下圖比較了上表中兩個機率列與預期機率的關係。
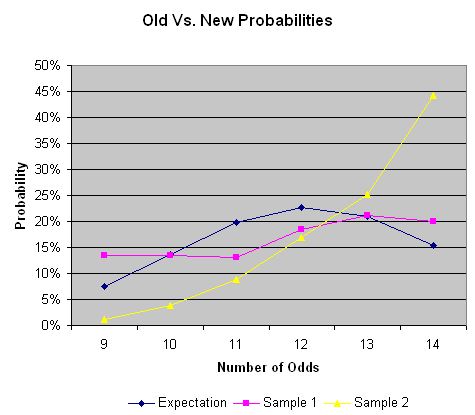
我向Station Casinos管理層諮詢了新牌的抽獎方式,他們說抽牌方式沒有任何變化。他們對我提出的相反證據沒有做出任何評論,並且由於我的“負面報道”,拒絕了進一步的合作。
註:「麥克的樣本」於11月1日下午3點在日落站採集。 「L的樣本」於10月30日上午9點和11點在博爾德站採集。
以下是我的初步研究,但現在已經過時了。
以下是我的證據,證明以下拉斯維加斯賭場出售的累積賓果卡並非完全隨機創建。
- 皇宮站
- 聖塔菲站
- 德州站
- 博爾德站
- 日落站
- 嘉年華牧場
- 嘉年華亨德森
- 山姆小鎮
拉斯維加斯的Station賭場經營一款名為「巨無霸賓果」(Jumbo Bingo)的連線賓果累積獎金遊戲。累積獎金的起始價為10萬美元。玩家必須在47次叫牌中全中(即卡牌上所有24個號碼全部覆蓋)才能中獎。如果第一週五家賓果店中無人中獎,則累積獎金(稱為巨無霸球)的叫牌次數將增加一次,達到48次。同樣,巨無霸球的叫牌次數也會每週增加一次,直到有人中獎為止。
顯然,為了節省時間,前37個被叫出的數字都是2到74之間的偶數。巨型賓果卡上預先標示了所有偶數,非常方便。遊戲開始時,主持人會詢問是否有人憑藉全是偶數的卡牌獲勝。然後,在無人認領中獎卡後,主持人將隨機抽出球,不考慮偶數球。如果在巨型球被叫出時無人獲得連身衣,則在52次叫牌後,將獲得5000美元的安慰獎,獎品是連身衣。如果沒有人認領,無論叫牌次數多少,第一個獲得連身衣的人都將獲得1199美元的獎金。與賓果遊戲一樣,如果多名玩家同時獲勝,獎金將平分。
Fiesta 賭場也有類似的遊戲,但規模較小。累積獎金起獎金額為 25,000 美元,安慰獎金額較小。所有雙數號碼都提前叫出。 Sam's Town 賭場則相反,奇數號碼提前叫出。
下表顯示了公平牌中,根據牌上奇數總數的機率分佈。我對公平牌的定義是,5 個“B”數字從 1 到 15 中隨機選擇,5 個“I”數字從 16 到 30 中隨機選擇,以此類推。另一種實現相同結果的方法是,從 1 到 75 中抽取數字,按所選數字填滿牌面,如果相應列已經填滿,則忽略這些數字。
奇數總數的機率 - 公平卡
| 數位 賠率 | 可能性 | 逆機率 |
|---|---|---|
| 0 | 0.000000000436 | 1 在 2293355030 |
| 1 | 0.000000022747 | 43962077 中的 1 |
| 2 | 0.000000534794 | 1869877 中的 1 |
| 3 | 0.000007530006 | 132802分之1 |
| 4 | 0.000071202834 | 1/14044 |
| 5 | 0.000480801205 | 2080年1月 |
| 6 | 0.002407676276 | 415分之1 |
| 7 | 0.00916827051 | 1/109 |
| 8 | 0.027013789916 | 37分之一 |
| 9 | 0.062346657338 | 1/16 |
| 10 | 0.113677702037 | 九分之一 |
| 11 | 0.164671200005 | 六分之一 |
| 12 | 0.1901222602 | 五分之一 |
| 十三 | 0.175132872532 | 六分之一 |
| 14 | 0.1285740634 | 八分之一 |
| 15 | 0.074984221403 | 1/13 |
| 16 | 0.034540809008 | 29分之一 |
| 17 | 0.012458867878 | 80分之一 |
| 18 | 0.003475365511 | 288分之一 |
| 19 | 0.00073657509 | 1358年1月 |
| 20 | 0.000115624911 | 8649分之1 |
| 21 | 0.000012937867 | 77292分之1 |
| 22 | 0.000000969822 | 1031117分之1 |
| 23 | 0.000000043401 | 23041075 中的 1 |
| 24 | 0.000000000872 | 1比1146677515 |
| 全部的 | 1 | 1 合 1 |
顯然,賠率極低的牌比賠率大多為奇數的牌更有優勢,中獎幾率也更高。在2002年7月的《拉斯維加斯顧問》雜誌上,我寫了一篇關於巨型賓果遊戲的文章,文章基於一個假設:這些牌是隨機產生的。那篇專欄的一位讀者告訴我,他相信這些牌不是隨機產生的,證據是他買了1500張牌,這些牌的賠率總數都在9到14之間。
為了證實所有卡片的賠率都在9到14之間的指控,我的助手Rob Feldheim在Palace Station收集了259張巨型賓果卡。然後我們計算了每張卡上的賠率,不出我所料,總賠率始終在9到14之間。下表顯示了每種賠率對應的總賠率,以及公平遊戲中的預期總賠率。
宮殿站卡,實際與預期
| 數位 賠率 | 數位 在樣本中 | 預期的 全部的 |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 0.000006 |
| 2 | 0 | 0.000139 |
| 3 | 0 | 0.00195 |
| 4 | 0 | 0.018442 |
| 5 | 0 | 0.124528 |
| 6 | 0 | 0.623588 |
| 7 | 0 | 2.374582 |
| 8 | 0 | 6.996572 |
| 9 | 三十五 | 16.147784 |
| 10 | 三十五 | 29.442525 |
| 11 | 三十四 | 42.649841 |
| 12 | 四十八 | 49.241665 |
| 十三 | 55 | 45.359414 |
| 14 | 52 | 33.300682 |
| 15 | 0 | 19.420913 |
| 16 | 0 | 8.94607 |
| 17 | 0 | 3.226847 |
| 18 | 0 | 0.90012 |
| 19 | 0 | 0.190773 |
| 20 | 0 | 0.029947 |
| 21 | 0 | 0.003351 |
| 22 | 0 | 0.000251 |
| 23 | 0 | 0.000011 |
| 24 | 0 | 0 |
| 全部的 | 259 | 259 |
賠率總數在9到14之間的機率是0.834524756。樣本中42.858088個賠率本應落在9到14的範圍之外,但實際上沒有一個落在這個範圍之外。在公平遊戲中發生這種情況的機率是0.834524756 259 = 4.4953 * 10 -21 ,即222,454,364,282,805,000,000分之一。
以下是對 2002 年 8 月 22 日上午 11:00 在 Fiesta Rancho 舉行的遊戲後獲得的 Grande 賓果卡進行同類測試的結果。
Fiesta Rancho 卡,實際與預期
| 數位 賠率 | 數位 在樣本中 | 預期的 全部的 |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 0.000002 |
| 2 | 0 | 0.000047 |
| 3 | 0 | 0.000655 |
| 4 | 0 | 0.006195 |
| 5 | 0 | 0.04183 |
| 6 | 0 | 0.209468 |
| 7 | 0 | 0.79764 |
| 8 | 0 | 2.3502 |
| 9 | 10 | 5.424159 |
| 10 | 6 | 9.88996 |
| 11 | 19 | 14.326394 |
| 12 | 18 | 16.540637 |
| 十三 | 18 | 15.23656 |
| 14 | 16 | 11.185944 |
| 15 | 0 | 6.523627 |
| 16 | 0 | 3.00505 |
| 17 | 0 | 1.083922 |
| 18 | 0 | 0.302357 |
| 19 | 0 | 0.064082 |
| 20 | 0 | 0.010059 |
| 21 | 0 | 0.001126 |
| 22 | 0 | 0.000084 |
| 23 | 0 | 0.000004 |
| 24 | 0 | 0 |
| 全部的 | 87 | 87 |
接下來是我從 Sams Town 抽取的累積獎金卡樣本的結果。
山姆小鎮卡牌,實際與預期
| 數位 偶數 | 數位 在樣本中 | 預期的 全部的 |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 0.000002 |
| 2 | 0 | 0.000055 |
| 3 | 0 | 0.000768 |
| 4 | 0 | 0.007263 |
| 5 | 0 | 0.049042 |
| 6 | 0 | 0.245583 |
| 7 | 0 | 0.935164 |
| 8 | 1 | 2.755407 |
| 9 | 1 | 6.359359 |
| 10 | 19 | 11.595126 |
| 11 | 二十五 | 16.796462 |
| 12 | 24 | 19.392471 |
| 十三 | 20 | 17.863553 |
| 14 | 12 | 13.114554 |
| 15 | 0 | 7.648391 |
| 16 | 0 | 3.523163 |
| 17 | 0 | 1.270805 |
| 18 | 0 | 0.354487 |
| 19 | 0 | 0.075131 |
| 20 | 0 | 0.011794 |
| 21 | 0 | 0.00132 |
| 22 | 0 | 0.000099 |
| 23 | 0 | 0.000004 |
| 24 | 0 | 0 |
| 全部的 | 102 | 102 |
根據與 Station Casinos 的 Stephen L. Cavallaro 的交談,我原本預計 Sam's Town 的賠率範圍是 10 到 15,或 9 到 14 個雙數。然而,我拿到了一張 8 個雙數的牌,也只拿到了一張 9 個雙數的牌。任何一張牌出現 8 到 14 個雙數的機率是 0.881703。102 張牌出現在這個範圍內的機率是 2.647786 * 10 -6 ,也就是 377,674 分之一。
此外,我還對 Suncoast 的普通賓果卡進行了類似的測試。 129 張樣本的實際結果和預期結果如下。
陽光海岸卡,實際與預期
| 數位 賠率 | 數位 在樣本中 | 預期的 全部的 |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 0.000003 |
| 2 | 0 | 0.000069 |
| 3 | 0 | 0.000971 |
| 4 | 0 | 0.009185 |
| 5 | 0 | 0.062023 |
| 6 | 0 | 0.31059 |
| 7 | 1 | 1.182707 |
| 8 | 6 | 3.484779 |
| 9 | 5 | 8.042719 |
| 10 | 17 | 14.664424 |
| 11 | 19 | 21.242585 |
| 12 | 二十九 | 24.525772 |
| 十三 | 20 | 22.592141 |
| 14 | 18 | 16.586054 |
| 15 | 10 | 9.672965 |
| 16 | 1 | 4.455764 |
| 17 | 3 | 1.607194 |
| 18 | 2 | 0.448322 |
| 19 | 0 | 0.095018 |
| 20 | 0 | 0.014916 |
| 21 | 0 | 0.001669 |
| 22 | 0 | 0.000125 |
| 23 | 0 | 0.000006 |
| 24 | 0 | 0 |
| 全部的 | 129 | 129 |
在129張牌中,超出9到14範圍的牌有21張,預期數字是21.34630654。這些牌很容易就通過了奇偶檢定。它們應該如此,因為沒有提前宣布奇數或偶數的遊戲。
下表顯示了公平遊戲中獲勝的機率,假設玩家必須獲得 50 個數字以內的所有數字。
獲勝機率 - 公平卡
| 數位 賠率 | 可能性 卡片的 | 可能性 卡牌勝利 | 全部的 可能性 |
|---|---|---|---|
| 0 | 0.000000000436 | 1 | 0.000000000436 |
| 1 | 0.000000022747 | 0.342105263158 | 0.000000007782 |
| 2 | 0.000000534794 | 0.110953058321 | 0.000000059337 |
| 3 | 0.000007530006 | 0.033902323376 | 0.000000255285 |
| 4 | 0.000071202834 | 0.009686378107 | 0.000000689698 |
| 5 | 0.000480801205 | 0.002564041264 | 0.000001232794 |
| 6 | 0.002407676276 | 0.000621585761 | 0.000001496577 |
| 7 | 0.00916827051 | 0.000135971885 | 0.000001246627 |
| 8 | 0.027013789916 | 0.000026317139 | 0.000000710926 |
| 9 | 0.062346657338 | 0.00000438619 | 0.000000273464 |
| 10 | 0.113677702037 | 0.000000604992 | 0.000000068774 |
| 11 | 0.164671200005 | 0.000000064821 | 0.000000010674 |
| 12 | 0.1901222602 | 0.000000004802 | 0.000000000913 |
| 十三 | 0.175132872532 | 0.000000000185 | 0.000000000032 |
| 14 | 0.1285740634 | 0 | 0 |
| 15 | 0.074984221403 | 0 | 0 |
| 16 | 0.034540809008 | 0 | 0 |
| 17 | 0.012458867878 | 0 | 0 |
| 18 | 0.003475365511 | 0 | 0 |
| 19 | 0.00073657509 | 0 | 0 |
| 20 | 0.000115624911 | 0 | 0 |
| 21 | 0.000012937867 | 0 | 0 |
| 22 | 0.000000969822 | 0 | 0 |
| 23 | 0.000000043401 | 0 | 0 |
| 24 | 0.000000000872 | 0 | 0 |
| 全部的 | 1 | 0 | 0.000006053319 |
下圖右側顯示,總中獎機率為 0.000006053319,即 1/165199。如果在公平遊戲中出現中獎,請注意,中獎機率最有可能出現在賠率 6 的牌上。在賠率低於 9 的公平遊戲中,中獎牌的機率為 94.15%。
當我計劃撰寫調查報告的消息傳開後,我被安排與Stephen L. Cavallaro(Station Casinos執行副總裁兼首席營運官)和Jonathan Swain(Palace Station副總裁兼總經理)見面。 Stephen坦言,這些牌的賠率是預先選定的,每張牌的賠率在9到14之間。他說,這樣做是為了創造公平的競爭環境,讓每張牌和每位顧客都有獲勝的希望。他也表示,最初的賠率範圍要廣得多,第一位獲勝者牌上的賠率一開始只有3個。此外,他還表示,Sam's Town和Fiesta Casinos也在做同樣的事情,而Station遊戲已獲得內華達州博彩管理委員會的完全批准。
在後續的電話訪談中,Stephen Cavallaro 告訴我,卡片的產生方式是電腦隨機選擇一組公平的數字。如果總賠率在 9 到 14 之間,計算機就會列印這張卡片;否則,計算機會丟棄這組數字,並繼續處理下一組。下表顯示了這種卡片產生方法下每個賠率數字的調整機率。
總奇數站卡機率
| 賠率數量 | 可能性 |
|---|---|
| 9 | 0.074709 |
| 10 | 0.136218 |
| 11 | 0.197323 |
| 12 | 0.227821 |
| 十三 | 0.209859 |
| 14 | 0.154069 |
| 全部的 | 1 |
總的來說,從組合中剔除最佳牌型的結果是,任何一張牌中獎的機率都會大幅降低。剔除最差的牌型並不能彌補這項缺陷。這種預選牌型的策略會導致累積獎金不斷增加。同時,賭場也減少了重新播種計量器的頻率。最終結果是累積獎金的贏家數量減少,總獎金也隨之減少。下表顯示了根據叫出的球數,公平牌型和站牌型中獎的預期機率。
預期獲勝機率
| 數位 通話次數 | 公平卡 | 車站卡 | 比率 |
|---|---|---|---|
| 四十七 | 1,122,373分之1 | 205,287,873分之1 | 182.91 |
| 四十八 | 583,217 人中 1 人 | 35,037,983分之1 | 60.08 |
| 49 | 308,005分之一 | 8,203,638分之1 | 26.63 |
| 50 | 165,199分之一 | 2,358,363分之1 | 14.28 |
| 51 | 89,925分之1 | 785,008分之一 | 8.73 |
| 52 | 49,648 人中 1 人 | 291,923分之1 | 5.88 |
| 53 | 27,784分之一 | 1/118,433 | 4.26 |
比率欄顯示使用 Station 賭場卡贏錢的難度是使用普通卡的多少倍。例如,如果必須在 50 個或更少的球內中獎,那麼贏錢的難度是普通卡的 14.28 倍。
我認為所有賓果卡都應該按照上述建議的方式真正隨機產生。除此之外,我認為如果一張卡不是隨機產生的,就應該公開其產生方式及其對玩家的影響。我強烈支持所有形式的賭博,公平且公開。但我發現內華達州的賓果遊戲並沒有做到這兩點。所以,賓果玩家要謹慎行事。
我感謝 Stephen Cavallaro 和 Jonathan Swaim 與我會面並對此事持開放態度。
回到賓果遊戲中的機率邁克爾·沙克爾福德,ASA






