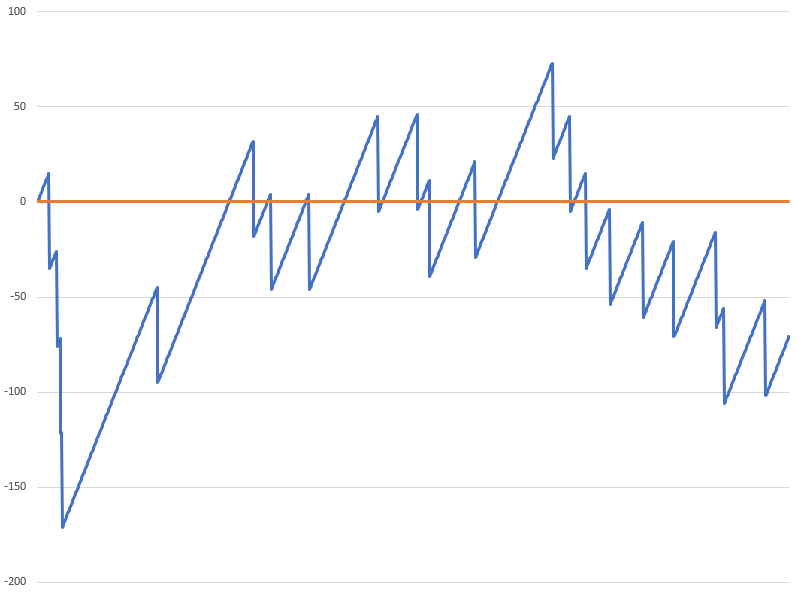
在這一頁
達朗貝爾投注系統
簡介
達朗貝爾投注系統是一種流行且經典的投注系統。與大多數投注系統一樣,它通常以小額盈利為代價,有時卻以巨額虧損為代價。與所有投注系統一樣,它不僅無法克服賭場優勢,甚至無法削弱賭場優勢。
與馬丁格爾、拉布謝爾和斐波那契投注類似,達朗貝爾投注也要求玩家以更大的投注追回損失。然而,它不像其他累進投注系統那樣激進,因此玩家在牌桌上的時間更長,波動性也更小。但代價是,整體目標達成機率較低。
規則
關於達朗貝爾系統,似乎唯一大家一致認同的是,玩家輸錢後加註一個單位,贏錢後減註一個單位。其他資料通常不會提及初始投注和輸贏基準。為了方便分析,我假設玩家初始投註一個單位,目標是贏一個單位。以下是整個系統的更正式的闡述。
- 玩家應確定自己的獲勝目標和資金規模。
- 玩家的「單位大小」應等於其獲勝目標。
- 玩家以一個單位的賭注開始。
- 如果玩家打平,那麼他重複同樣的賭注。
- 否則,如果最後的賭注結果是贏,並且玩家實現了他的獲勝目標,那麼他就會高興地離開。
- 否則,贏錢後,如果下注金額為單位,則保持不變。否則,他將下注金額減少一個單位。 *
- 否則,在輸掉之後,玩家將增加一個單位的賭注。 **
- 玩家下注。
- 回到規則 4,直到玩家實現其獲勝目標或失去其全部資金。
*:如果這樣的賭注會導致玩家在獲勝時超出其獲勝目標,則將賭注大小降低到下次下注時能夠準確實現獲勝目標的金額。
**:如果玩家沒有足夠的錢進行下一次下注,則將下注金額降至玩家剩餘的金額。
一般評論
達朗貝爾投注系統的一個有趣之處在於,它並不像平注投注系統那樣,輸贏的順序無關緊要。就投注結果而言,唯一重要的就是輸贏的次數。即使輸的次數多於贏的次數,達朗貝爾投注系統也能顯示獲利,只要差距不是太大。下表顯示了不同輸贏次數下的淨利潤。例如,玩家可以贏22場輸28場,仍然可以顯示一個單位的獲利。
淨勝分(以總勝負計算)
| 勝利 | 損失 | 淨贏 |
|---|---|---|
| 2 | 3 | 1 |
| 3 | 4 | 2 |
| 4 | 6 | 1 |
| 5 | 7 | 2 |
| 6 | 8 | 3 |
| 7 | 10 | 1 |
| 8 | 11 | 2 |
| 9 | 12 | 3 |
| 10 | 十三 | 4 |
| 11 | 15 | 1 |
| 12 | 16 | 2 |
| 十三 | 17 | 3 |
| 14 | 18 | 4 |
| 15 | 19 | 5 |
| 16 | 21 | 1 |
| 17 | 22 | 2 |
| 18 | 23 | 3 |
| 19 | 24 | 4 |
| 20 | 二十五 | 5 |
| 21 | 二十六 | 6 |
| 22 | 二十八 | 1 |
| 23 | 二十九 | 2 |
| 24 | 三十 | 3 |
| 二十五 | 31 | 4 |
| 二十六 | 三十二 | 5 |
| 二十七 | 33 | 6 |
| 二十八 | 三十四 | 7 |
| 二十九 | 三十六 | 1 |
| 三十 | 三十七 | 2 |
| 31 | 三十八 | 3 |
| 三十二 | 三十九 | 4 |
| 33 | 40 | 5 |
| 三十四 | 41 | 6 |
| 三十五 | 四十二 | 7 |
| 三十六 | 43 | 8 |
| 三十七 | 45 | 1 |
| 三十八 | 46 | 2 |
| 三十九 | 四十七 | 3 |
| 40 | 四十八 | 4 |
| 41 | 49 | 5 |
| 四十二 | 50 | 6 |
| 43 | 51 | 7 |
| 四十四 | 52 | 8 |
| 45 | 53 | 9 |
| 46 | 55 | 1 |
| 四十七 | 56 | 2 |
| 四十八 | 57 | 3 |
| 49 | 58 | 4 |
| 50 | 59 | 5 |
當失敗次數等於或大於獲勝次數時,淨贏的一般公式為 W - D*(D+1)/2,其中:
W = 獲勝次數
D = 勝負差。換句話說,虧損減去獲利。
在上面的例子中,22 勝 28 負,淨勝為 22 - 6*7/2 = 21。
儘管能夠在適度虧損的會議中獲勝,但大多數時候是以小額勝利為代價的,而在極其寒冷的會議中,巨大的勝利會在長期內抵消掉這些小額勝利。
模擬結果
為了展示使用達朗貝爾演算法的預期結果,我編寫了一個遵循上述規則的模擬程序,該程序基於各種投注和遊戲。該模擬程式使用了梅森旋轉隨機數產生器。每次模擬的初始投注和獲勝目標均為一個單位。我測試了以下資金規模的模擬程式:10、25、50、100 和 250 個單位。
第一個模擬是基於百家樂中的閒家投注。模擬規模超過 730 億次。提醒一下,閒家投注的理論莊家優勢為 1.235%。
百家樂模擬 — 玩家投注
| 統計 | 10個單位 | 25個單位 | 50個單位 | 100個單位 | 250個單位 |
|---|---|---|---|---|---|
| 達到獲勝目標的機率 | 90.36% | 95.74% | 97.73% | 98.78% | 99.45% |
| 平均投注次數 | 2.422 | 3.297 | 3.719 | 4.169 | 4.837 |
| 平均投注單位 | 4.857 | 8.727 | 12.670 | 18.456 | 30.939 |
| 每場預期勝利 | -0.060 | -0.108 | -0.157 | -0.228 | -0.382 |
| 輸錢與賭注金額之比 | 1.234% | 1.236% | 1.235% | 1.235% | 1.235% |
第一個模擬是基於擲骰子遊戲中的過關投注。模擬規模超過 650 億次。需要提醒的是,過關投注的理論莊家優勢為 1.41%。
擲骰子模擬 — 透過投注
| 統計 | 10個單位 | 25個單位 | 50個單位 | 100個單位 | 250個單位 |
|---|---|---|---|---|---|
| 達到機率獲勝目標 | 90.34% | 95.72% | 97.72% | 98.78% | 99.44% |
| 平均投注數 | 2.423 | 3.300 | 3.724 | 4.176 | 4.850 |
| 平均總投注額 | 4.399 | 7.908 | 11.489 | 16.752 | 28.134 |
| 每場預期勝利 | -0.062 | -0.112 | -0.162 | -0.237 | -0.398 |
| 輸錢與賭注金額之比 | 1.414% | 1.414% | 1.414% | 1.414% | 1.414% |
下一個模擬是基於擲骰子遊戲中的「不過線」投注。模擬規模超過 760 億次。提醒一下,「不過線」投注的莊家優勢為 1.364%。
擲骰子模擬 — 不通過投注
| 統計 | 10個單位 | 25個單位 | 50個單位 | 100個單位 | 250個單位 |
|---|---|---|---|---|---|
| 達到機率獲勝目標 | 90.35% | 95.73% | 97.72% | 98.78% | 99.44% |
| 平均投注數 | 2.423 | 3.299 | 3.723 | 4.175 | 4.847 |
| 平均總投注額 | 4.523 | 8.131 | 11.811 | 17.218 | 28.903 |
| 每場預期勝利 | -0.062 | -0.111 | -0.161 | -0.235 | -0.394 |
| 輸錢與賭注金額之比 | 1.364% | 1.364% | 1.364% | 1.365% | 1.363% |
下一個模擬是基於單零輪盤賭中的任何等額投注。模擬規模超過 250 億次。提醒一下,理論莊家優勢為 1/37 = 2.7027%。
輪盤模擬 — 單零
| 統計 | 10個單位 | 25個單位 | 50個單位 | 100個單位 | 250個單位 |
|---|---|---|---|---|---|
| 達到機率獲勝目標 | 89.81% | 95.30% | 97.40% | 98.52% | 99.26% |
| 平均投注數 | 2.456 | 3.381 | 3.851 | 4.371 | 5.190 |
| 平均總投注額 | 4.485 | 8.200 | 12.125 | 18.119 | 31.920 |
| 每場預期勝利 | -0.121 | -0.222 | -0.328 | -0.490 | -0.863 |
| 輸錢與賭注金額之比 | 2.702% | 2.703% | 2.702% | 2.703% | 2.702% |
下一個模擬是基於雙零輪盤賭中的任何等額投注。模擬規模超過 250 億次。提醒一下,理論莊家優勢為 2/38 = 5.2632%。
輪盤模擬 — 雙零
| 統計 | 10個單位 | 25個單位 | 50個單位 | 100個單位 | 250個單位 |
|---|---|---|---|---|---|
| 達到機率獲勝目標 | 88.68% | 94.37% | 96.65% | 97.91% | 98.75% |
| 平均投注數 | 2.520 | 3.544 | 4.112 | 4.782 | 5.942 |
| 平均總投注額 | 4.660 | 8.800 | 13.463 | 21.083 | 40.571 |
| 每場預期勝利 | -0.245 | -0.463 | -0.708 | -1.109 | -2.134 |
| 輸錢與賭注金額之比 | 5.263% | 5.263% | 5.263% | 5.263% | 5.261% |