運動 - 常問問題
針對Vargas與Quartey之間的拳擊賽、⺫前的概率為Quartey -240、 Quartey +190. 如果我押注$100在Vargas、或是押注$100在Quartey, 這 樣要如何運作?
押注$240在Vargas將會贏到$100. 押注$100在Quartey將會贏到$190. 當 然, 你可以押注任何的⾦額, 但是贏注的⽐例還是相同的。如果你押注 $100在Vargas, 那麼你將會贏到 $100 × (100/240)=$41.67.
在投注spread點差讓分的sports betting運動簽賭, 在我看來, 贏家要⽀付 10%的抽佣, ⽽不是輸家⽀付。我需要知道什麼嗎?
你可以從兩⽅⾯來看。例如, 前提是你押注$11以贏得$10的賭局。 輸家⽀付: 可以說它是⼀種even-money等額賠率的押注, 如果你贏的話、 有$1可退還的費⽤。所以, 只有輸家在最後⽀付這個費⽤。 贏家⽀付: ⼀個公平的even-money等額賠率的押注、針對$11將會贏到 $11. 然⽽, 如果押注贏的話, 贏家只拿到$10. 失去的⼀元美⾦可以看成是 ⼀筆佣⾦或是費⽤。 個⼈⽽⾔, 我將兩種⽀付看待成⼀次4.54% house edge賭場優勢的形式, 假設贏的機率為50%.
除了Nevada內華達州之外, 還有沒有任何的州可以合法押注在職業運動 上、例如棒球或是⾜球?
除了Nevada內華達州之外, 還有沒有任何的州可以合法押注在職業運動 上、例如棒球或是⾜球?
我最近看到⾜球的賭盤總⾦額。其形式為100個⽅框的格線、沿著X與Y軸
線並且有0-9回合、對應最後的⽐賽分數。我並不是⾜球迷、也從未押注
這樣的賭盤, 不過我是⼀位賭客, 並且不認為這是很好的押注。
我認為你應該知道我所提出的這種型態。每⼀個⽅框花費$5、並且在每⼀
個quarter場次⽀付。如果你的⽅框贏了、你就贏到$125、並且有可能贏
到所有的4個quarters場次, 如果最後的次數保持相同、則針對100⽐1的⽀
付賠率⽽贏到$500.
對我推銷這款押注的⼈試著告訴我, 贏到$500的概率是100⽐1. 我並不認
同。⾸先, ⽅框俱有0 + 7較⾼的贏注機會、相較於2 + 9的⽅框。然⽽, 0 +
7的概率整場⽐賽維持最後2個次數必須是⾼的。如果⽅框是透過隨機⽅式
來幫你選定, 你能否告訴我贏到$500獎⾦的⼤約概率是多少?
假設格線當中的⽅框欄位是由隨機選出的, 那麼在任何⼀個quarter場次贏 的概率將會是1/100. 假設每⼀個quarter場次都是獨⽴事件, 其實並⾮如此, 贏到所有四個quarters場次的概率將會是 (1/100)4 = 100百萬分之⼀。
讀到你最近的「Ask the Wizard請問巫師」單元。你說過sport betting運 動簽賭將會是可以⽤來謀⽣的⽅式之⼀。你能否闡述更詳細⼀些?它是否 類似於Blackjack⼆⼗⼀點算牌賭徒那般俱有較⾼的優勢可以勝過賭場? 多謝。
很不幸地, 我不能再說得更多了。Sports betting運動簽賭並⾮我的強項, 雖然我有時間的話會想要學到更多。我必須得說, 很難⽐較運動簽賭與算 牌兩者的機率。算牌是相當技術層次的。利⽤運動簽賭來賺錢需要更多的 判斷能⼒還有更多議題的選項。有各種策略可以⽤在運動簽賭⽽賺到錢, 例如查看arbitrage套利的賽局、在不同spreads點差讓分賭盤的不同賭場 押注雙⽅, 利⽤不尋常的proposition bets主題投注, 或是透過相關的 parlays累進押注來進⾏。我會推薦Stanford Wong的「Sharp Sports Betting精準運動簽賭」以得到更多資訊在運動簽賭的贏注議題上。
我⾒過各種NFL美式⾜球賭盤研究者吹噓關於他們對於贏注選號的百分⽐, 如果是隨機選號者、在超過1, 3, 5個球季得到50%, 55%, 60%的機率是如 何?
以下的列表顯⽰參與從50%到60%機率的分佈狀況, 每增加1%, 從球季1到 5為數列。這是基於259場⽐賽的球季。我也假設整體的百分⽐是被四捨 五⼊歸整過的。例如, 如果簽賭者從259場⽐賽當中選取132場, 針對百分 ⽐50.97%, 他將只有50%的選項是有效的, 因為他並沒有達到51%. 如果這 些誇張的簽賭者以對⾃⼰有利的⽅式來進位歸整數字、這我倒不會感到意 外。.
簽賭者百分⽐在NFL美式⾜球當中的機率
| ⽐率 | 1球季 | 2球季 | 3球季 | 4球季 | 5球季 |
| 0.5 | 0.5 | 0.517523 | 0.5 | 0.512393 | 0.5 |
| 0.51 | 0.354641 | 0.314437 | 0.282985 | 0.257059 | 0.234993 |
| 0.52 | 0.267178 | 0.178085 | 0.125486 | 0.101366 | 0.074229 |
| 0.53 | 0.160065 | 0.086589 | 0.049447 | 0.025155 | 0.015098 |
| 0.54 | 0.106982 | 0.035817 | 0.013066 | 0.004959 | 0.001926 |
| 0.55 | 0.053095 | 0.012519 | 0.002569 | 0.000687 | 0.000152 |
| 0.56 | 0.023385 | 0.00282 | 0.000373 | 0.000051 | 0.000007 |
| 0.57 | 0.012645 | 0.00067 | 0.000053 | 0.000003 | 0 |
| 0.58 | 0.00453 | 0.000133 | 0.000004 | 0 | 0 |
| 0.59 | 0.00213 | 0.000022 | 0 | 0 | 0 |
| 0.6 | 0.000617 | 0.000003 | 0 | 0 | 0 |
我喜歡你對於NFL美式⾜球賭盤的⾒解。賭票每張要花費$25、並且包含 三個隨機的球隊、按照給定的次序。每週持有最⾼三個得分球隊的賭票持 有者、以正確的排序, 將會贏到$1000. 每⼀張賭票實際的價值是多少?
在32⽀球隊的NFL美式⾜球的球季有17週的正常時期。任何⼀週贏的機率 為 32*31*30 = 29760分之⼀。每張賭票的期望值為$1000*17/29760 = 57.12美分。所以期望回報率為2.28%, 或者賭場優勢為97.72%!
對不起打擾你, 如同你在網⾴當中所陳述的, 然⽽你可有⽤過你的數學能⼒ 去找出運動簽賭當中不尋常的概率、或者計算出⼀種⽅式、並可以根據那 樣的資訊⽽保證其回報率?
最近幾年我花了許多時間鑽研運動簽賭, ⽐起其他的賭博形式要花更多的 時間。除⾮你能夠透過不同的賭盤同時在兩家組頭簽賭以互相對抗, 這樣 的機會相當罕⾒, 不然就不保證能夠在運動簽賭會有賺錢的⽅式。現在透 露任何秘訣還太早、不過我會尋找任何察覺到的押注、對於玩家有利、並 且投⼊我的賭注。你可以⾒到某些我最近的資訊在我的sports betting appendix 2 運動簽賭附錄2.
如果⼀所⼤學的⾜球隊贏得⽐賽1的機會是10%、贏得⽐賽2的機會是 30%、兩場⽐賽皆輸的機會是65%, 他們剛好贏到⼀場⽐賽的機會是多 少?
如果我們假設⽐賽都是各⾃獨⽴的, 那麼輸掉兩場⽐賽的機率將是 90%*70%=63%. 不過既然你說輸掉兩場⽐賽的機率實際上為65%(這⽐起 63%還要⾼), 也就是說兩場⽐賽是相關的。如果輸掉兩場⽐賽的機率是 65%、只輸掉⽐賽2的機率是70%, 那麼贏得⽐賽1並且輸掉⽐賽2的機率 必須是5%. 運⽤相同的邏輯、輸掉⽐賽1並且贏得⽐賽2的機率必須是 25%. 這樣贏得兩場⽐賽的機率只剩下5%. 所以剛好贏得⼀場⽐賽的機率 為 25%+5% = 30%.
我的問題是特別針對星期⼀晚上的⾜球⽐賽、今晚的(Dallas @ Washington). 現在Washington華盛頓已經下⾬好幾⼩時。這場⾬會持續 整個⽐賽直到隔天。我納悶下⾬會對NFL美式⾜球的押注有什麼影響?你 可以給我其他⽅⾯的建議嗎?
我不知道下⾬會對總分產⽣什麼影響。然⽽我知道精準的簽賭者⾮常認真 考慮天氣的因素、並且會隨著溫度、降⾬量、⾵速、還有其他這類的因素 ⽽轉移押注的賭盤。
嗨巫師, 假設我想出⼀種運動簽賭的system妙⽅, 每年需要押注$1K以得到 $80K的回報。為了要得到這樣的回報率、每年差不多要投注250-300次。 運動賭盤的組頭是否會禁⽌我、就像賭場禁⽌算牌者那樣?你是否可以公 開地成為⼀位成功的運動簽賭者、或者你必須像算牌者那樣低調⾏事?
⾸先, 我懷疑任何⼈可以⽤1K的押注⽽賺到80K。不要對我⽤「system妙 ⽅」這個字眼。要回答你的問題, 因為⼤部份最佳的運動簽賭者都是公開 的。即使⼀家運動賭盤組頭禁⽌⼀位職業賭客的⾏動、或是他們86家的產 業, 還是可以輕易透過別⼈過去簽賭。我曾經參加過Fezzik的Super Bowl 超級杯proposition bet主題投注研討會, 他是⼀位職業賭客, ⽽當時他是戴 著Halloween萬聖節⾯具來演講的。
你對於選取Super Bowl超級杯賭盤terminal digit尾數有何建議?
我所⾒到的公開賭盤已經被隨機化成表格、標註為每⼀⾏與每⼀列的隨機 數字。然⽽如果你可以選取以下列表的實際terminal digit尾數、顯⽰出每 ⼀⽀球隊最後分數每個尾數的頻率, 基於1983到2003年每⼀場NFL美式⾜ 球的⽐賽。
NFL美式⾜球各⽅的尾數
數字 |
頻率 |
機率 |
0 |
1887 |
17.75% |
1 |
1097 |
10.32% |
2 |
348 |
3.27% |
3 |
1382 |
13.00% |
4 |
1608 |
15.13% |
5 |
396 |
3.73% |
6 |
848 |
7.98% |
7 |
1945 |
18.30% |
8 |
631 |
5.94% |
9 |
488 |
4.59% |
總計 |
10630 |
100% |
所以這份列表顯⽰7是最佳的選項, 接著是0, 4, 與 3.
我想⾒到你的 「NFL美式⾜球 picks精選」 更多數字模型的細節。嘿, 如果 你開始運⽤這個去做出實際的押注, 這是否就會被定義為⼀種「betting system押注妙⽅」?
我更喜歡其他的某些部分。我的模型創造出它在每⼀場⽐賽所估計的公平 spread點差讓分, 我所列出的是差異⼤的⽽⾮選取的分數。個⼈來說, 我會 押注更多在較⼤差異的項⺫。然⽽要等到證明我的選項是對的、不然那就 是過分狂妄的⾃信了。
關於你的NFL美式⾜球 picks精選, 他們的⽐重是否都相同, 或者是說, 根據 你的模型、可有任何的選項強過其他的?
我更喜歡其他的某些部分。我的模型創造出它在每⼀場⽐賽所估計的公平 spread點差讓分, 我所列出的是差異⼤的⽽⾮選取的分數。個⼈來說, 我會 押注更多在較⼤差異的項⺫。然⽽要等到證明我的選項是對的、不然那就 是過分狂妄的⾃信了。
你內⼼是否是Packers的球迷?我是的。看起來你是⽤⼼在押注、⽽ Packers卻扼殺了你偉⼤的NFL美式⾜球 picks精選. 。即使是Packers在你 也沒有出現很⼤的百分⽐。只是想你可能喜歡觀察⽽已.
這無關乎對於球隊的忠誠問題。我的程式在2004年球季結束時將他們評 ⽐為第五⽀最佳球隊, ⽽且我持續⽤那個排名進到2005年球季。然⽽或許 它最近的表現不佳。這是我需要思考的問題。
我⾒過某⼈提供2-1在⼀位玩家、超過100場⽐賽選取57%的spread點差讓 分。儘管我認為57%是個艱困的數字, 給定這樣⼩的樣品數、我認回這或 許是⼀個好的押注。我的問題是這樣 - 如果簽賭者是50%的選擇, 忽視和 局, (也就是丟擲銅板的狀況)這會是個好的押注嗎?如果不是的話、針對 這個選項整體的百分⽐將是多少?
針對2⽐1的押注, 好的押注最⼤樣品數是14場⽐賽。隨機選擇的話、你將 有39.5264%的機會選到57%或更好的, 或這8場或更多場是對的。你必須 有好過33.3333%的機率才能做出好的押注。21場是接近公平的, 然⽽機率 在33.1812%是有點太⼩。選取的場次愈⼤、則所需的百分⽐則愈低。例 如, 如果所需的最⼤數字是選取1000次, 要超過1/3贏的機會將會是507 次。在1000次選項當中得到507次或更多次對的機率為34.05%.
我是⻑時間的⾜球迷也是簽賭者。我對於你在⾜球的數字模型⾮常有興 趣、並且嘗試要做出我⾃⼰的模型, 因為我知道⾃⼰無法單單靠⾃⼰的知 識⽽贏到⾜球的押注(我累了)。所以我想到要利⽤統計的⽅式來嘗試。我 ⽤的是SPSS統計程式。我的問題是, 你在你的模型當中使⽤的是什麼變 數?
在模型當中唯⼀會⽤到的是分數與主場的優勢。有時候我尋求外場的選項 在主要的傷員名單, 例如Ben Roethlisberger在第6週, 或者New Orleans在 San Antonio的主場⽐賽。
歡迎回來Wizard巫師。你不再只是Wizard of Odds概率巫師, 然⽽從你的 表現, 你也是NFL美式⾜球 Picks精選巫師. 我在賭場的賭盤只有51.7%. 我有⼀個簡單的請求。如果沒有花太多時間的話、你是否每週可以列出你 對於所有⽐賽的選項列表?
感謝。你可能是在第四星期送出這則信息, 那對我來說是很糟糕的⼀週。 現在, 五週之後我的紀錄是17與13, 平均為56.7%, 那還不錯、但也不是很 好。我認為那對於我電⼦報的讀者來說是額外福利、我將會給出我對於所 有⽐賽的想法。
既然你現在有針對 football⾜球 ⽅⾯、我對於parlays累進押注有⼀個問 題。我最近押注我所選取的over超過/under低於在Steelers/Chargers MNF⽐賽的每個4 quarters場次、並且贏了。(只有quarters場次, 不是半 場或是整局)。現在簽賭的組頭不願意⽀付、因為他們說那有關聯性。我 相信⽐賽的每個quarter場次是相互獨⽴的、但是他們不同意。Wizard巫 師是怎麼想的呢?
⾸先, 任何⼈接受這個押注就應該尊重它, 單就原則⽽論。紳⼠會尊重他的 債務, 尤其是賭債。其⼆, 雖然我並沒有研究過它、我認為quarters場次實 際上並⾮是相關的。例如, 如果第⼀個quarter場次有低的總分, 很可能每 ⼀⽅球隊在第⼆個quarter場次開始將會有較好的球場位置, 這樣很可能在 第⼆個quarter場次得到⾼分, 依此類推。
Wizard巫師, 我有⼀個問題是關於我的「真實」贏注百分⽐針對 NFL美式 ⾜球 picks精選. 。我告訴我的朋友們、我在過去5年(那是真的)都沒有輸過 ⼀次球季, 押注從第3-16週、每週平均選取2-3次。我個⼈對於⽐賽的感覺 較重、基本上我若是相信概率對我有利、我就會押注更多。例如, 今年我 押注9次, 4次為$55, 其中贏了3次。我押注3次$110的賭注, 其中贏了1 次。不過我喜歡的兩場⽐賽、其中押注⼀場$330, 還有$600 (even line等 額賠率賭盤), 並且兩個都贏了。⼀點也不錯, 我是9次中6次的66%機率, 不 過我這樣押中我認為更加確定的⽐賽, 這真的意味著80%的機率(⾼效 能)。這樣對你⽽⾔有意義嗎?我⼤致上都是這麼做, 結果就是, 當我計算 過去5年以來(60-70%的選項, 但是~80%當納⼊我押注多少錢時)。你能否 告訴我⼀個簡單的⽅式去納⼊押注⾦額的因素, 是否我的假設是正確的? ⾮常多謝你。
我最近關於這點想了很多。以我所⾒, ⼀個贏注百分⽐應該等於每場⽐賽 的加權⽐重。你在你投資的整體回報率應該也有分開的統計, 然⽽任何的 統計數值應該列出邊際因素、⽇期、賭盤來源、點差讓分、概率(通常 為-110). 另⼀件你沒有提及的事是, 你在3或7的spread點差讓分lay -120是 怎麼做的。它將⽐較容易得到好的贏注百分⽐、如果你納⼊這些押注選項 的話。所以我相信在投資的回報率應該會維持even輸贏持平、如果是flat betting持平押注的話。另⼀件困擾我的事是、關於某些簽賭者, 他們所引 述得賭盤是找不到的。我認為到處看看是好的、但是引述的賭盤應該是不 難找到的。我承認這個球季我並沒有親⾃做這些事, 因為當我開始的時候 並沒有想到這些事。明年, 如果我還這樣做的話, 我會將我的結果建檔、並 且當成是⼀筆投資來看待。
你會建議玩賭盤或是spread點差讓分在你的 NFL美式⾜球 picks精選、或 是無論如何都無所謂?
無論押注的理由為何, 通常在賭盤押注在較弱的⼀⽅⽐較好、並且偏好對 抗spread點差讓分。
我總是想要做出某些⾃⼰的NFL簽賭押注、但是我很難找到⼀個網站, 希 望是免費的, 去下載球隊的歷史資料。有任何建議嗎?可下載的檔案是我 所偏好的, 因為剪貼網⾴內容並不實際、然⽽若是需要的話我也願意去 做。還有, 像是天氣與球場的狀況也會很有助益。
個⼈⽽⾔, 我使⽤來⾃ Mr. NFL, 的NFL美式⾜球資料庫, 那要花費$99. 如 果還有⽐它更好更便宜的、我倒是不知道。
針對你的 NFL美式⾜球 picks精選 你的系統似乎⽐重太過偏向弱隊。49場 ⽐賽當中你只有挑出8場⽐賽。其中你選取⼀⽀球隊在even line等額賠率 的賭盤。這是你系統的瑕疵、或者⼈們更加傾向選取強隊、⽽你的系統嘗 試從他們的傾向當中佔到便宜?我並沒有做過分析, 不過從我的觀察, 有幾 次贏注在spread點差讓分的範圍、卻沒有球隊真正贏過⽐賽。
以歷史上來說, 弱隊是較好的押注。這裡是1983年球季每⼀場⽐賽的結 果、直到2005年球季的第10週。
強隊贏得spread點差讓分: 2554場⽐賽
弱隊贏得spread點差讓分: 2724場⽐賽
⽐賽確實終⽌在spread點差讓分: 150場⽐賽
所以決定押注在弱隊已經贏到51.61%的⽐賽。這也是知名的拘謹押注者 偏好押注強隊, 這就創造出弱隊的價值。
今年我們的「Football Bet Taker⾜球押注組頭」提⾼over/under押注的利 潤從10%到20%, 並且消除parlays累進押注的10%利潤。所以取代押注2 個分別的o/u押注, 我押注2個parlaying累進押注、⽀付賠率為2.5⽐1. 這會 是好的策略運⽤嗎?
在straight bets直接投注的期望回報率將是 (0.5*1 + 0.5*(-1.2))/1.2 = -8.33%. 在parlay累進押注的期望回報率將是 0.25*2.5 + 0.75*-1 = -12.5%. 然⽽如果我只押注兩場遊戲、並且想要贏的話, 我會選擇parlay累 進押注。更重要的是, 我會基於原則去杯葛這個組頭, 因為我之前從未聽過 lay -120在straight bets直接投注上⾯。
在你的網站有兩個不同的單元, 你提到⼀般來說、最好是押注賭盤的弱 隊、⽽⾮強隊。然⽽, 你在Sports Betting運動簽賭 附錄3當中指出, 押注 強隊、其賭盤的賭場優勢較低。這兩者是否⽭盾?任何的押注不就都要押 注最低的賭場優勢嗎?
說得好。我思考之後、決定移除我的sports betting運動簽賭 附錄3. 它是 基於假設公平賭盤剛好是兩個賭盤之間。例如在上次的Super Bowl超級 盃, ⼀般的賭盤為Seattle +160 與 Pittsburgh -180. 我的附錄是基於不切實 際的假設、公平賭盤將會是 +/- 170. 真實的賭盤是根據市場調控的。刻板 的賭盤傾向於強隊, 創造出弱隊的價值。假設Pittsburgh為4分的強隊、這 在歷史紀錄是公平的、建議4分的偏好程度、⼤約有61%贏的機會。這樣 將會讓Seattle在公平賭盤+156, ⽽-156在Pittsburgh球隊。提醒你, 那多數 賭場的賭盤為+160/-180. 當然Pittsburgh這次贏得⽐賽, 不過從歷史紀錄來 說, 我很肯定你在賭盤投注弱隊將會是較好的選項。
我是在刻板的NFL美式⾜球賭盤、並且選到⾮常好的⽐數。7與4針對 Pittsburgh、4與0針對Seattle. 我好奇今年會贏的機率是多少?
對於我的讀者們或許不懂這個問題, ⼀個Super Bowl超級盃賭盤是10乘以 10的格線。玩家將會買⼊設定⾦額的每個⽅格, 將買家的名字寫⼊每個⽅ 格之中。當100個⽅格都已經被買下、橫欄與縱欄就會被隨機從0到9給予 標⽰。有點像是⼀組10乘以10的表格, 只是橫欄與縱欄抬頭被隨機混合標 ⽰。混合的理由是某些terminal digits尾數⽐其他的更有可能, 這你在以下 的列表會⾒到。例如, 任何⼈最後有Seattle 0, Pittsburgh 1的⽅框將會贏 得賭盤, 因為最後的分數為Seattle 10, Pittsburgh 21.
以下的列表顯⽰從1983到2005年球季、每⼀場NFL美式⾜球⽐賽、每種 組合的頻率。應該注意的是, 2-point conversion rule轉換規則⼤約在1998 年出現, 這將會多少修正某些分佈的效應。
NFL美式⾜球當中的尾數 - Away客隊與Home主隊的總計
| 客隊 | 主隊 | 總計 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ||
| 0 | 126 | 104 | 34 | 160 | 138 | 37 | 99 | 237 | 64 | 32 | 1031 |
| 1 | 73 | 40 | 17 | 41 | 103 | 21 | 36 | 117 | 67 | 31 | 546 |
| 2 | 25 | 15 | 1 | 20 | 30 | 9 | 13 | 33 | 9 | 12 | 167 |
| 3 | 194 | 69 | 33 | 66 | 102 | 40 | 102 | 132 | 43 | 40 | 821 |
| 4 | 122 | 133 | 27 | 78 | 108 | 27 | 48 | 215 | 59 | 35 | 852 |
| 5 | 32 | 12 | 12 | 21 | 21 | 9 | 13 | 36 | 22 | 5 | 183 |
| 6 | 91 | 47 | 17 | 75 | 57 | 7 | 28 | 57 | 25 | 39 | 443 |
| 7 | 217 | 115 | 35 | 135 | 195 | 47 | 65 | 125 | 69 | 47 | 1050 |
| 8 | 43 | 59 | 12 | 24 | 41 | 23 | 20 | 38 | 15 | 7 | 282 |
| 9 | 48 | 28 | 17 | 33 | 40 | 14 | 29 | 33 | 14 | 7 | 263 |
| 總計 | 971 | 622 | 205 | 653 | 835 | 234 | 453 | 1023 | 387 | 255 | 5638 |
以下的列表顯⽰基於上述列表當中總分的每個組合的機率。
NFL美式⾜球當中的尾數 - Away客隊與Home主隊的機率
| 客隊 | 主隊 | 總計 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ||
| 0 | 0.0223 | 0.0184 | 0.006 | 0.0284 | 0.0245 | 0.0066 | 0.0176 | 0.042 | 0.0114 | 0.0057 | 0.1829 |
| 1 | 0.0129 | 0.0071 | 0.003 | 0.0073 | 0.0183 | 0.0037 | 0.0064 | 0.0208 | 0.0119 | 0.0055 | 0.0968 |
| 2 | 0.0044 | 0.0027 | 0.0002 | 0.0035 | 0.0053 | 0.0016 | 0.0023 | 0.0059 | 0.0016 | 0.0021 | 0.0296 |
| 3 | 0.0344 | 0.0122 | 0.0059 | 0.0117 | 0.0181 | 0.0071 | 0.0181 | 0.0234 | 0.0076 | 0.0071 | 0.1456 |
| 4 | 0.0216 | 0.0236 | 0.0048 | 0.0138 | 0.0192 | 0.0048 | 0.0085 | 0.0381 | 0.0105 | 0.0062 | 0.1511 |
| 5 | 0.0057 | 0.0021 | 0.0021 | 0.0037 | 0.0037 | 0.0016 | 0.0023 | 0.0064 | 0.0039 | 0.0009 | 0.0325 |
| 6 | 0.0161 | 0.0083 | 0.003 | 0.0133 | 0.0101 | 0.0012 | 0.005 | 0.0101 | 0.0044 | 0.0069 | 0.0786 |
| 7 | 0.0385 | 0.0204 | 0.0062 | 0.0239 | 0.0346 | 0.0083 | 0.0115 | 0.0222 | 0.0122 | 0.0083 | 0.1862 |
| 8 | 0.0076 | 0.0105 | 0.0021 | 0.0043 | 0.0073 | 0.0041 | 0.0035 | 0.0067 | 0.0027 | 0.0012 | 0.05 |
| 9 | 0.0085 | 0.005 | 0.003 | 0.0059 | 0.0071 | 0.0025 | 0.0051 | 0.0059 | 0.0025 | 0.0012 | 0.0466 |
| 總計 | 0.1722 | 0.1103 | 0.0364 | 0.1158 | 0.1481 | 0.0415 | 0.0803 | 0.1814 | 0.0686 | 0.0452 | 1 |
雖然在Super Bowl超級盃有⼀⽀正式的主場球隊, 我認為我們可以忽略這 點。讓我們也忽略關於兩⽀球隊的種種諸事、緊盯以上的歷史紀錄。最 後, 讓我們忽略Super Bowl超級盃不會以和局結束, 這將會讓4/4的⽐數較 不可能會贏。所以讓我們以尾數不同來做出平均。例如你的Pittsburgh 7、Seattle 4的機率, ⽅格平均將會是Away客隊 7, Home主隊 4; 還有 Away客隊 4, Home主隊 7. 針對你的每個⽅格做出以下的機率結果。
Pitts 7, Sea 4: (0.0346+0.0381)/2 = 0.0364
Pitts 7, Sea 0: (0.0385+0.0420)/2 = 0.0403
Pitts 4, Sea 4: 0.0192
Pitts 4, Sea 0: (0.0216+0.0245)/2 = 0.0231
所以你贏到⼀次的總機率為11.90%. 考量你只有涵蓋4%的⽅格數。
雖然你並沒有特別問到, 這裡是每個尾數有多常發⽣的數值。它顯⽰出整 體最常出現的排序為 7043168952.
NFL美式⾜球當中的尾數 - Away客隊與Home主隊的總計
| 尾數 |
客隊 | 主隊 | 總計 |
|---|---|---|---|
| 0 | 1031 | 971 | 2002 |
| 1 | 546 | 622 | 1168 |
| 2 | 167 | 205 | 372 |
| 3 | 821 | 653 | 1474 |
| 4 | 852 | 835 | 1687 |
| 5 | 183 | 234 | 417 |
| 6 | 443 | 453 | 896 |
| 7 | 1050 | 1023 | 2073 |
| 8 | 282 | 387 | 669 |
| 9 | 263 | 255 | 518 |
最後, 這裡是每個terminal digit尾數的機率
NFL美式⾜球當中的尾數 - Away客隊與Home主隊的機率
| 尾數 |
客隊 | 主隊 | 總計 |
|---|---|---|---|
| 0 | 0.1829 | 0.1722 | 0.1775 |
| 1 | 0.0968 | 0.1103 | 0.1036 |
| 2 | 0.0296 | 0.0364 | 0.033 |
| 3 | 0.1456 | 0.1158 | 0.1307 |
| 4 | 0.1511 | 0.1481 | 0.1496 |
| 5 | 0.0325 | 0.0415 | 0.037 |
| 6 | 0.0786 | 0.0803 | 0.0795 |
| 7 | 0.1862 | 0.1814 | 0.1838 |
| 8 | 0.05 | 0.0686 | 0.0593 |
| 9 | 0.0466 | 0.0452 | 0.0459 |
關於這個議題的更多資訊, 造訪 Football Squares Mathematical and Statistical Strategy ⾜球⽅格數學與統計的策略.
⼈們會誤解、在拉斯維加斯的運動簽賭限額相當⾼, 在我的經驗中, 只適⽤ 於⾜球、並不全然都是這樣的。你能否告訴我在拉斯維加斯、運動簽賭對 於四種主要運動的限額?多謝你的時間。
我並沒有將曲棍球列⼊主要的運動、因為它的活動很少。我被告知Coast 賭場俱有最⾼的限額。我知道在Stone沒有最⾼的設限, 不過他們會隨著個 案⽽接下⼤額的押注。這裡是我認為他們在⼀般的⽐賽可能會接受的⾦ 額。
NFL美式⾜球邊注: $50,000
NFL美式⾜球總分: $5000
MLB職棒⼤聯盟賭盤: $10,000
MLB職棒⼤聯盟總分: $2000
NBA職籃邊注: $10,000
NBA職籃總分: $2,000
許多線上組頭提供halftime下半場賭注, 我想知道你對於「dutching分攤⾵ 險」的意⾒。有時候它是很明顯的, 然⽽你考慮在下半場押注在與你相反 的球隊、重點是什麼?還有, 如果你發現有利的狀況時、你應該押注多少 ⾦額?
我假設你所說的「dutching分攤⾵險」就是hedging避險。在我的 ten commandments of gambling賭博⼗誡 當中第六條, 「Thou shalt not hedge thy bets 你不應該保失你的押注。」我唯⼀會做出例外是hedge bet兩邊下注俱有正⾯的期望值、或是資本⾦額可能會⼤受影響的時候。
你在拉斯維加斯賭場的college football⼤學⾜球押注所能贏到的最⾼⾦額 是多少、如果你在兌換賭票當時並沒有提供你的個⼈資料?我想知道我可 以贏到多少錢(每次投注)、並且在他們⽀付我現⾦時不會受到質問。
$10,000. 現⾦交易超過$10,000, 無論是運動或其他項⺫, 將會需要⼀份 CTR(cash transaction report現⾦交易報告)。你也可以要求以籌碼來⽀付, 雖然當你兌現籌碼時也需要相同的CTR現⾦交易報告。
除了免費網站之外, 你能否推薦⼀個網站、我可以得到職業運動簽賭的資 訊、以⽉費或是贏注百分⽐收費。
不。我不會為任何宣傳來背書的。
你談過你在NFL美式⾜球押注弱隊的事。你是否每次只押注在主場的弱 隊、或者那是更加複雜的情況?最重要的, 如果它是主場弱隊、決定的賭 盤是什麼...早期的賭盤或者是剛好在⽐賽之前的賭盤。多謝。
我並⾮只是盲⺫押注在弱隊, 即使我必須只讓lay -105, 這是本球季在拉斯 維加斯城中區Plaza的案例。如果我在運動簽賭只有偵測到很⼩的優勢, 那 我就不會押注。在運動投注我總是假設某個誤差範圍, 因為畢竟是⼈在⽐ 賽, ⽽⾮統計學。然⽽, 如果我可以找到⽐賭盤還要更好的優勢、或是某位 值得信賴的簽賭者推薦的側⾯訊息, 那我會很樂於去投注的。
感謝這個很棒的網站!我⽗親與我對於hedging bets雙⽅押注有過爭論、 真的需要你的幫助!這個特殊情況涉及Super Bowl超級盃的⼀個押注。在 球季開始時(我⽗親不記得是哪⼀年)我的叔叔押注New England將會贏得 超級盃。這個押注⽀付60⽐1的賠率。就在超級盃之前(當時New England 正在⽐賽)我的叔叔⼜轉向他的押注(⽗親不記得細節)放棄可能的$6,000獎 ⾦、但是取⽽代之的是保證$3,000的獎⾦。我認為那是個笨蛋的押注、不 過我⽗親不肯聽我的。我爭辯說, 在這個節⾻眼轉換押注、他就放棄了期 望值、⽽聰明的簽賭者是絕對不會這樣做的。我⽗親辯說放棄期望值還 好、因為涉及的⾦錢還有事實上這個押注並不常出現, 就如同幫你的房⼦ 保險那般。當然, 我爭論房⼦的所有權本質上不同於運動簽賭、那是誰都 無法避免的。你的想法如何呢?請幫助我們擺平此事!
在我的Ten Commandments of Gambling賭博⼗誡當中的第七條說道, 「Thou shalt not hedge thy bets你不應該保失你的押注。」所以如果投降 的$3,000價值對他⽽⾔是事關重⼤的⾦額, ⽽且如果贏注的機率不超過 50%, 那我就不會吝惜他的決定。然⽽, 除⾮這事是在2002年, New England贏球的機率遠⾼於50%. 在另外兩年的超級盃, 2004年 與 2005年, 他們有7分的優勢。我會估計那兩年贏球機率⼤約是71%. ⼀個公平的 surrender value投降價值將會是 0.71 × $6100 (包含他原初退回的押注⾦ 額) = $4,331. 這個押注的賭場優勢, 等於⼀筆even money等額賠率押注在 其他的球隊, 為 29%-71% = 42%. 所以, 如果我對於⽐賽年份是對的, 那他 就做出很糟的決定。他可以在開放市場的賭盤獲得更好的概率。任誰只提 供$3,000、若⾮對⽐賽無知、就是不公平佔取便宜。有趣的是, New England在他們最近的超級盃三場⽐賽都贏了三分。
NFL美式⾜球⽐賽最後和局的機率是多少?
從1983年到2007年的球季, 超過5,901場正規球季⽐賽當中有10場和局。 規則要求⼀場⽐賽在季後賽不可以和局告終。所以其機率、基於過去的⽐ 賽, 為0.17%, 或是⼤約590分之⼀。
在NFL美式⾜球⽐賽兩⽀球隊之間最後分數差異、與該次⽐賽pointspread 點差讓分的standard deviation標準均⽅差不同之處是什麼?
為了其他讀者們的益處著想, 讓我們檢視最近Super Bowl超級盃的案例, 以說明你所問的問題。Patriots有12分的優勢, 但是輸了3分。所以⽐賽以 15分的point spread點差讓分結束。如果我正確了解這個問題, 你是在問關 於這個差異的standard deviation標準均⽅差。針對每個聯盟研究的平均差 異幾近於零。這裡是我所得到的標準均⽅差:
NFL美式⾜球 13.31 (基於 2000年到2007年的球季)
⼤學⾜球 15.72 (基於 1993年到2007年的球季)
NBA職籃 11.39 (基於 1987年到2003年的球季)
所以, 2008年Super Bowl超級盃結束 15/13.31 = 1.13 標準均⽅差偏離期
望值。我忽略了discrete distribution不連續分佈的調整因素, 為了儘量保持
範例的簡單性。在1.13標準均⽅差的機率或是更加偏離期望值, 兩者皆為
25.85%. 這可以⽤Excel找得到, 利⽤公式 2 × normsdist(-1.13).
⾝為想要押注弱隊的運動簽賭者, 並且想到處看看賭盤的狀況, 我知道你能 夠找到各種額外半分的價值。在你的典型NFL美式⾜球或是NBA職籃⽐ 賽, 每個半分對你⽽⾔的價值是多少?我知道⼀位簽賭者在-110的公平賭 盤需要達到52.4%才能break even輸贏持平。我知道市場上規定的賭盤, 但是你會說每個半分真的價值是多少?如果你可以在所押注的每場⽐賽得 到額外的半分、那會讓你的break even輸贏持平點真正落在50%. 有什麼 ⽅式可以計算嗎?多謝。
如同我在我的 NBA職籃專⾴當中所顯⽰的, 當買⼊半分時、贏的機率為 51.01%、輸的機率為47.01%, 平⼿則為1.98%, 假設簽賭者從來不會在 spread點差讓分0 或 -1時買⼊半分, 這是他不應該做的事。如果你只為了 額外的半分⽽必須讓lay 110, 期望回報率將會是 (0.5101 - 1.1×.4701)/1.1 = -0.64%.
已知球隊A每次⽐賽平均得到1.5分, 球隊B每次⽐賽平均得到1.2分, AB兩 隊⽐賽的機會如何:
1) A得分超過B
2) B得分超過A
3) ⽐賽以和局結束。
所提供的資訊⾜以計算每次結果的機率嗎?
個別分數應該不是有關聯、不應納⼊計算, ⽽每⼀⽀球隊個別的分數與平 均分數同樣重要。如果我們可以假設1.5與1.2為⽐賽的期望得分, 考慮攻 ⽅與守⽅兩隊, ⽽我們忽略掉相關的因素, 那麼我們能夠得到不錯的估算值 在你的三種機率上。Super Bowl超級盃有許多像是這樣的⽐例, 但是基於 誰將會有更多的touchdowns達陣的分、field goals射⾨得分、 interceptions攔截等等。
第⼀步是運⽤Poisson distribution波以松分佈去估計每隊每次得分的機 率。通⽤的機率公式為 ⼀個球隊有g次得分, 平均為m, 亦即 e-m × mg/g!. 在Excel, 你可以套⽤公式 poisson(g,m,0). 以下的列表顯⽰針對兩⽀球隊0 到10次得分的機率, 運⽤這個公式。
每⽀球隊0到8次得分的機率
| 得分次數 | 球隊A | 球隊B |
| 0 | 0.223130 | 0.301194 |
| 1 | 0.334695 | 0.361433 |
| 2 | 0.251021 | 0.216860 |
| 3 | 0.125511 | 0.086744 |
| 4 | 0.047067 | 0.026023 |
| 5 | 0.014120 | 0.006246 |
| 6 | 0.003530 | 0.001249 |
| 7 | 0.000756 | 0.000214 |
| 8 | 0.000142 | 0.000032 |
下⼀步相當乏味, 但是你必須做出每⽀球隊0到8次得分的81種可能組合的 matrix矩陣。這是將機率乘上球隊A的x得分、球隊B的y得分, 從以上列表 的數值。以下的列表顯⽰每種得分組合從0-0到8-8的機率。
下個列表顯⽰根據每種得分組合的贏家, T代表tie和局。
合併兩⽀球隊的贏家
| 球隊A得分次數 | 球隊B得分次數 | ||||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| 0 | T | B | B | B | B | B | B | B | B |
| 1 | A | T | B | B | B | B | B | B | B |
| 2 | A | A | T | B | B | B | B | B | B |
| 3 | A | A | A | T | B | B | B | B | B |
| 4 | A | A | A | A | T | B | B | B | B |
| 5 | A | A | A | A | A | T | B | B | B |
| 6 | A | A | A | A | A | A | T | B | B |
| 7 | A | A | A | A | A | A | A | T | B |
| 8 | A | A | A | A | A | A | A | A | T |
最後, 你可以運⽤Excel的sumif函數去加總相關的欄位、針對所有三種可 能的押注結果。在這個案例的機率為:
A隊贏 = 44.14%
B隊贏 = 30.37%
和局 = 25.48%
附錄C在Stanford Wong所著的 Sharp Sports Betting精準運動簽賭 給出像 這類 贏/輸/和 的押注機率。針對這個例⼦, 他列出44%, 30%, 25%. 如果 任何⼈知道關於這種問題的簡單公式, 願聞其詳。
再接再厲: 我收到來⾃Bob P.的⼀封電郵, 每次有數學議題他總會緊盯在 後。這裡是他所寫的.
檢視不相關的2個Poissons分佈。它是a href="http://en.wikipedia.org/wiki/Skellam_distribution" target=_blank>Skellam(對我來說是新詞)。反正, 這個問題可以標⽰為 P(Z=0), P(Z>0), P(Z<0), Z為Skellam的參數 1.5 與 1.2.
如果你還沒做過的話, 你應該很樂意知道
P(Tie) = P(Z=0) = .254817
P(A beats B) = P(Z>0) = .441465
P(B beats A) = P(Z<0) = 1 - .254817 - .441465 = .303718
幾乎就是你的答案。
輸⼊Skellam的維基百科有提到 Bessel functions⾙索函數, 那是我很怕再 算下去的部分。所以, 我就摘錄Bob的話語來總結這個命題。
我有好運氣押注過球隊曾經連輸五場⽐賽、也押注過球隊連贏五場⽐賽。 我爭論那不像是骰⼦與輪盤, 你說骰⼦或球是沒有記憶的, ⼀⽀職業運動隊 伍不能無限度贏或輸下去。我選擇連續五場⽐賽、在分析之後, 當轉變會 更常發⽣。對我⽽⾔他們在哪裡⽐賽、或是誰開始投球、受傷等等因素都 無所謂。你認為我的想法對嗎?
我認為這些是好的押注, 但並⾮是你陳述的理由。⼀個運動隊伍可以, 在理 論上, ⼀直輸下去。這些是好的押注, 理由之⼀是他們⼤多數時間都會是很 ⼤的弱隊, ⽽弱隊⼀般來說⽐起強隊的押注要好得多。另⼀個理由, 刻板的 押注者⼀般在這些情況都會押注另⼀⽅, 這會製造出你所押注⽅式的價 值。
我是⼀組NFL美式⾜球賭盤競賽六⼈之⼀。我們每個⼈必須選取球季當中 的70場⽐賽以對抗主要的網路運動簽賭組頭, 那有⼀個20分錢的賭盤。其 中⼀位參賽者提供⼀個over/under主題投注在球季最後最⾼的得分。他的 賭盤獲利8.5個單位。讓我們假設球季尚未開始, ⽽那位參賽者是有經驗的 運動簽賭者。你認為那個賭盤怎樣、還有你怎麼分析它?
要問你⾃⼰最⼤的問題是, 像這樣的主題投注, ⼀個給定選項最後將會贏、 輸、或平⼿的機率是多少。從我的單元在 betting the NFL美式⾜球的押 注, 我們可以⾒到有2.8%的⽐賽正好落在賭盤之上。讓我們就說3%好了, 這樣⽐較簡單。讓我們稱呼 p 為贏的機率, 給定那次押注完成了。對於單 純的隨機選號者, p 顯然就是50%. 這很容易透過只選取弱隊⽽獲得進展。 如同我之前提過的專⾴顯⽰, 超過25個球季持平押注在弱隊將會導致贏注 ⽐例為51.5%. 它也很容易透過押注⽐較有利賭盤的⽅式來獲得進展。這 兩者之間, 我認為不難達到52%. 所以我會對這些⼈有信⼼、⾄少會達到 52%.
所以, 假設完成的贏注為52%, 整體的機率為:
贏: 50.44%
平局: 3.00%
輸: 46.56%
運⽤基本的統計學, 很容易⾒到每次選號的期望贏注, 讓laying -110, 為-0.0078. 每次選號的標準均⽅差為1.0333. 期望贏注超過70次選號 為-0.5432, 其標準均⽅差為 701/2×1.0333 = 8.6452. 贏到8.5個單位是 9.0432個單位超過期望值, 或是9.0432/8.6452=1.0460標準均⽅差對於 Gaussian Curve⾼斯曲線右側的期望值。我認為我們可以忽略不連續分佈 的調整、因為平⼿的因素, 還有某些⽐賽並⾮-110/-110, 將會導致相當平 滑的曲線、下降到0.05個單位的因⼦。
所以, 任何⼀位玩家完成超過1.046標準均⽅差期望值以上的機率為 14.77%. 那個圖形可以在任何Gaussian curve⾼斯曲線的列表找得到, 或 者在Excel透過公式 =1-normsdist(1.046). 所有六位玩家完成低於1.046的 機率為 (1-0.1477)6=38.31%. 那麼, 所有六位玩家⾄少有⼀位玩家完成 1.046以上的標準均⽅差的機率為61.69%. 那樣檢視⼀個可靠押注讓laying -110. 我顯⽰它在-161是公平的。
以下的列表顯⽰給定不同數值的p值、超過8.5次贏注的機率。或許設定主 題投注的個⼈假設p值接近到51%.
NFL美式⾜球賭盤的主題投注
| 正確選號機率 | 超過贏注機率 |
| 50.0% | 41.16% |
| 50.5% | 46.18% |
| 51.0% | 51.33% |
| 51.5% | 56.53% |
| 52.0% | 61.69% |
| 52.5% | 66.72% |
| 53.0% | 71.52% |
你是如何認為Patriot call第⼀次down、當他們第四次down在⾃⼰的28碼 線 — 還有他們領先6分?! 在那樣情況做出第⼀次down的概率是多少, 你會 怎麼做呢?
為了其他讀者的利益, 這是參考 2009年⼗⼀⽉15⽇的賽事 、其中Patriots 領先Colts六分。當時第四個quarter還剩下1:57, 那是第四次down、⼤約 1.5碼, ⽽且球在Patriots隊的28碼線。Patriots的教練 Bill Belichick 做出有 爭議的決定以贏的勝利、並且進到第⼀次down在第四場quarter, ⽽⾮punt 踢球射⾨。
對於此事在 Las Vegas Review Journal. 有⼀則很好的專欄。它引述職業 賭客兼精算師Steve Fezzik說的話、其概率對於第⼀次down是有利的。我 完全同意。⼀般來說, 我認為其他的教練太常punt踢球, 並且太過害怕冒 險。為了議論我的論點、我問過數學達⼈兼運動簽賭者Joel B., 他對於分 析⾜球的概率⽐我強多了。他提供以下的概率:
- Patriot做出第⼀次down的機率: 60%
- Patriot做出第⼀次down、並且贏的機率: 100%
- Patriot失去第⼀次down、並且贏的機率: 50%
- Patriot如果punt踢球、並且贏的機率: 75%
所以, 做出第⼀次down、並且贏球的機率為 60%×100% + 40%× 50% = 60% + 20% = 80%. 那⽐punting踢球的75%機率要⾼。
這個星期天早上quarterbacks四分衛們可以盡其所能去誹謗Belichick, 不 過我讚許他的決定。他不應該因為⽐賽結果⽽受到審判, 不過是否概率有 利於當時他所做的決定。我強烈感到他們是的。⼀週之後在 Ravens/Steelers 的⽐賽 、Ravens在第四場進擊並且得分。雖然那是不同的狀況, 我可還沒聽到有任何⼈對於那次決定有微詞異議。
為了公平的理由, 我提供⼀則抱持相反意⾒的連結, 標題為 Belichick’s fourth-and-reckless 由ESPN.com的Bill Simmons報導。
假設有兩場⾜球⽐賽、我覺得俱有玩家的優勢。讓我們說每⼀場有55%的 贏注機會, ⽽我必須讓lay 110. 哪⼀種必較可以獲利, 直接押注⽐賽、或是 當成單⼀的parlay累進押注?
很好的問題。Straight up直接押注, 每次押注的優勢為 0.55×(10/11) - 0.45 = 0.05. 當成parlay累進押注, 其優勢為 (0.55)2×((21/11)2-1)-(1-(0.55)2) = 10.25%. 所以, 看起來似乎累進押注是可以最⼤化優勢的⽅式。
然⽽, 當成parlay累進押注的變數較⼤。如果你有在追隨 Kelly Criterion, 那麼你必須在⼩額的押注在parlay累進押注時保護你的資⾦。在這個例⼦, 最佳的Kelly直接押注是資本的5.48%、如果兩場⽐賽重疊, 5.50%如果你 的第⼀場⽐賽在你押注的第⼆場⽐賽結束之前, ⽽針對parlay累進押注則 是3.88%. 將賭注乘以優勢, 我們得到0.00275直接押注(基於5.50%的優 勢)、還有0.00397的累進押注。所以, 累進押注導致較⼤的獲利。
我考量這款問題的⼀般案例, 也查看3隊與4隊的parlays累進押注與賭盤押 注。假設所有押注有⼩的優勢, 當成基本原則, 如果每場賽事贏注的機率⼩ 於33%, 那麼你就應該直接押注。如果每場機率落在33% 與 52%之間, 那 麼你就應該做出2隊的parlay累進押注。如果每場機率落在52% 與 64%之 間, 那麼你就應該做出3隊的parlay累進押注。如果每場機率⼤於64%, 那 麼你就應該做出4隊的parlay累進押注。如果你是做直接的押注, 那麼你⼤ 約等於是在做2隊或3隊的parlays累進押注, 假設你開始就有優勢的話。
我應該強調的是, 如果你是位休閒的賭客、準備對抗賭場優勢(什麼樣的運 動簽賭者會承認那樣?), 那麼就直接押注以最⼩化賭場優勢。
在NFL美式⾜球做出2-point conversion兩分轉換的機率是多少?
從2000年到2009年的NFL球季, 不包含2009年的季後賽, 有過567次失敗 的2-point conversion兩分轉換嘗試, 318次成功的嘗試。這樣做的話, 成功 的機率為 318/(567+318) = 35.9%.
我真的喜歡你的 Wizard of Vegas拉斯維加斯巫師 網站精簡的指引。我也 有⼀個問題關於 sports betting guide運動簽賭指南. 。這個圖表並沒有⼀些 ⽐賽的總分或是賭盤, 所以我假設賭場並沒有提供這些押注。這是否相關 於point spread點差讓分的⼤⼩、或者其他的原因⽽不在那裡?

那張圖是由Leroy的加盟者所拍攝, 那是⼀個⼩型保守的運動簽賭組頭。他 們傾向於先拿掉spread點差讓分、之後還有總分與賭盤的部分。
這也很不尋常會提供明顯不平衡⽐賽的賭盤, 例如Eastern Michigan vs. Central Michigan俱有23分的spread點差讓分。這樣的⽐賽很難設定精確 的賭盤, 不平衡⾏動的⾵險較⼤。押注賭盤在⼤的spread點差讓分、最佳 的賭場是Hilton. 最後, 如果spread點差讓分相當⼩, 像是1分或1.5分, 則⼤ 多數組頭根本就不想推出賭盤, 因為押注在spread點差讓分可能導致相同 的結果。
這個問題曾被提出與討論在我的夥伴網站討論區 Wizard of Vegas拉斯維 加斯巫師.
感謝你親筆撰寫這本預測Super Bowl超級盃確實分數預測的書。然⽽, 期 望值是否太低?我發現贏注的機率⼤約是300分之⼀。
我認為概率⽐起有專業經驗的估計還要更好。這裡是我針對任何NFL美式 ⾜球⽐賽確實結果的選號基本策略。
- 運⽤total總分與spread點差讓分, 估計每⽀球隊的總點數。例如, 如果針
對Super Bowl超級盃, 我們運⽤total總分57、spread點差讓分-5, 設定
c=Colts的分數, s=Saints的分數, 則...
(1) c+s=57
(2) c-5=s
將⽅程式(2)代⼊⽅程式(1)當中:
c+(c-5)=57
2c-5=57
2c=62
c=31
s=31-5=26
到這裡為⽌的問題是, 你所得到的數值並不像是單⼀球隊的得分。例如, 單 ⼀球隊總分24的機率為6.5%, 但是總分25的機率只有0.9%. 以下的列表顯 ⽰單⼀球隊的總機率, 基於2000-2009年的球季。所以我們將要估計每⽀ 球隊的總分、基於實際field goals射⾨與touchdowns達陣的組合。
- 假設最強的kicks踢球2 field goals得分。
- 假設弱隊kicks踢球1 field goals得分。
- 各⾃減去field goal得分。在Super Bowl超級盃的例⼦, 這會剩下Colts = 25 touchdown達陣得分, Saints = 23 touchdown達陣得分。
- 將touchdown達陣得分除以7, 得到估計的touchdowns達陣分數。 c=3.57 TD, s=3.29 TD
- 將估計的touchdowns達陣分數歸整為最接近的整數值。c=4, s=3.
- 依照這個⽅法, 我們得到總分 c=(4×7)+(2×3)=34, s=(3×7)+(1×3)=24.
運⽤這個⽅法在1983-2009年球季的所有6,707場⽐賽, 將會導出69次正確 的選號, 成功率為1.03%. 最近⼀次正確的估計是2009年第13週Titans/ Colts的⽐賽。那場⽐賽Colts的spread點差讓分為-6.5, 總分為46. 得分數 為Titans 17, Colts 27.
挑惕的想法認為較好的簡單策略是選取兩⽀球隊中最接近的單⼀球隊總 分。使⽤這種⽅法只有51次的贏注, 贏注機率為0.76%. 依我所⾒, 將強隊 與弱隊分開成field goals射⾨得分2 與 1是很重要的。單⼀球隊總分在2000-2009年球季的NFL美式⾜球
| 單⼀球隊總分 | 取樣的總分 | 機率 |
| 0 | 93 | 1.75% |
| 1 | 0 | 0.00% |
| 2 | 0 | 0.00% |
| 3 | 148 | 2.79% |
| 4 | 0 | 0.00% |
| 5 | 2 | 0.04% |
| 6 | 114 | 2.15% |
| 7 | 210 | 3.96% |
| 8 | 9 | 0.17% |
| 9 | 76 | 1.43% |
| 10 | 316 | 5.96% |
| 11 | 9 | 0.17% |
| 12 | 49 | 0.92% |
| 13 | 289 | 5.45% |
| 14 | 238 | 4.49% |
| 15 | 55 | 1.04% |
| 16 | 170 | 3.21% |
| 17 | 373 | 7.03% |
| 18 | 33 | 0.62% |
| 19 | 92 | 1.73% |
| 20 | 368 | 6.94% |
| 21 | 234 | 4.41% |
| 22 | 64 | 1.21% |
| 23 | 218 | 4.11% |
| 24 | 347 | 6.54% |
| 25 | 47 | 0.89% |
| 26 | 103 | 1.94% |
| 27 | 282 | 5.32% |
| 28 | 159 | 3.00% |
| 29 | 52 | 0.98% |
| 30 | 127 | 2.39% |
| 31 | 242 | 4.56% |
| 32 | 23 | 0.43% |
| 33 | 57 | 1.07% |
| 34 | 164 | 3.09% |
| 35 | 76 | 1.43% |
| 36 | 27 | 0.51% |
| 37 | 68 | 1.28% |
| 38 | 108 | 2.04% |
| 39 | 11 | 0.21% |
| 40 | 21 | 0.40% |
| 41 | 62 | 1.17% |
| 42 | 31 | 0.58% |
| 43 | 6 | 0.11% |
| 44 | 24 | 0.45% |
| 45 | 33 | 0.62% |
| 46 | 1 | 0.02% |
| 47 | 7 | 0.13% |
| 48 | 28 | 0.53% |
| 49 | 15 | 0.28% |
| 50 | 1 | 0.02% |
| 51 | 5 | 0.09% |
| 52 | 7 | 0.13% |
| 53 | 0 | 0.00% |
| 54 | 2 | 0.04% |
| 55 | 1 | 0.02% |
| 56 | 4 | 0.08% |
| 57 | 1 | 0.02% |
| 58 | 1 | 0.02% |
| 59 | 1 | 0.02% |
| 總計 | 5304 | 100.00% |
這個問題曾被提出與討論在我的夥伴網站討論區 Wizard of Vegas拉斯維 加斯巫師.
在NFL美式⾜球4th quarter場次之前onside kick邊場踢球成功的機率是多 少。我是說, Super Bowl超級盃當中的動作絕對是聰明的, 可是Saints的教 練是否有統計數值⽀持他的決定、或者只是靈機⼀動⽽已?
根據⼀篇傑出的⽂章在 advancedfootballanalytics.com, 歷來成功的機率 為26%. 然⽽, ⼤多數的onside kick邊場踢球, 其他球隊會這樣期待, 那將會 降低成功的機率。對於surprise onside kicks意外的邊場踢球, 成功的機率 為60%! 這篇⽂章的⽤意是, 聰明策略就是更常去做surprise onside kicks 意外的邊場踢球。我同意; 對於Saints球隊來說是⼀次聰明的舉動。
這個問題曾被提出與討論在我的夥伴網站討論區 Wizard of Vegas拉斯維 加斯巫師.
什麼樣的動態會影響⾜球總分的押注、當球季進⾏當時, 天氣會變壞、還 有更多關於球隊最近表現的資訊?有多容易(或多難)去發現賭盤的錯誤?
為了協助回答這個問題, 我畫出NFL美式⾜球每週的平均得分數, 基於 1983-2009年每個球季。以下的圖表顯⽰其結果。
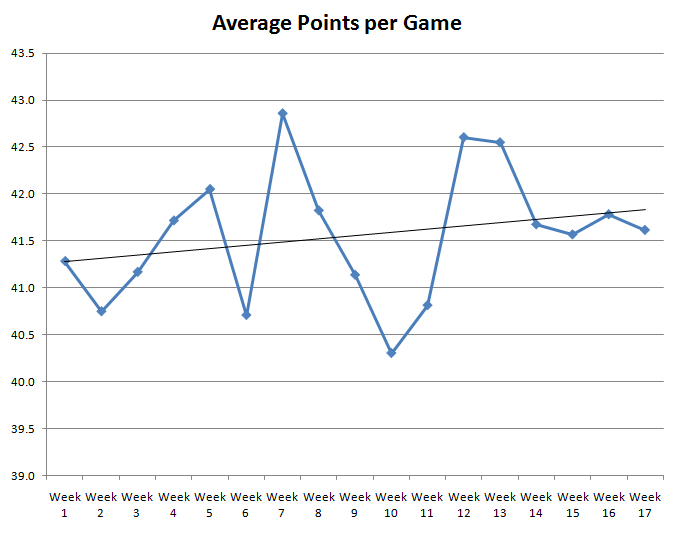
你可以看⾒, 曲線是起起伏伏的。⿊⾊實線是least-squared best fit line最 ⼩平⽅誤差的迴歸線, 總體來說是朝上的趨勢。所以當球季進⾏時, 氣溫下 降, 平均得分漸漸增加, 不過那可能輕易是因為隨機的變化。
這是⺫前為⽌我所能說的。針對天氣影響運動押注的⼀般意⾒, 我轉給我 的朋友Jason Been, 他是這個議題的專家。在這裡他曾說過:
在⼤多數案例, ⾵是天氣最主要影響⽐賽的因素; 不過, 這並⾮唯⼀的⼀項 因素。在棒球與其他的⼾外運動, 陰影可以是相同的效應, 尤其是在球季早 期與晚期的下午⽐賽。下⾬或下雪在⾜球來說、並⾮⼤多數⼈所想的那 般、會是很⼤的因素, 因為同樣都會影響到攻擊與防守的兩⽅。⼀個案例 將會是防守⽅對抗⻑程的接球者。下⾬和下雪將會同樣拖延雙⽅, 因此不 會有哪⼀⽅得到優勢。⾵在⾜球踢球時可以消除傳球的效⼒。我就⾒過⽐ 賽當中, 傳球的⼀⽅被逼著在強勁側⾵當下每次都得要跑著傳球。這並不 常發⽣, 不過⾵的因素最終將會影響到⽐賽的進⾏.這個問題曾被提出與討論在我的夥伴網站討論區 Wizard of Vegas拉斯維 加斯巫師.
在NFL美式⾜球, 平均⽽⾔, ⼀隊得分之後另⼀隊也得分的機率是多少?
根據2000-2009年NFL美式⾜球的球季, 答案是57%.
如果⼀⽀NFL球隊在上次⽐賽徹底被擊敗, 在下⼀場的⽐賽是否還要押注 他們、或者反向押注他們?相同的問題也針對在⼀次⽐賽⼤勝之後。我總 會聽到, ⼀⽀球隊在⼤輸之後、將會「想要證明⾃⼰」, ⽽⼀⽀球隊在⼤贏 之後、或許因為過度⾃信⽽變得懶散。怎樣才是真的?
我顯⽰出在輸掉21分或更多分之後、球隊將會涵蓋51.66%的spread點差 讓分。然⽽, 那是在誤差範圍之內。以下的列表顯⽰對抗上⼀場⽐賽的 spread點差讓分結果, 根據同⼀⽀球隊之前⽐賽的輸或贏狀況。結果從未 偏離50%、總是維持在standard deviation標準誤差之內。基本上, 我找不 到輸贏之間在spread點差讓分、以及上⼀場⽐賽輸贏多少分的統計關聯 性。
贏/輸/和局對抗Spread點差讓分、根據上⼀場⽐賽勝負的範圍
| 上⼀場⽐賽結果 | 贏注對抗點差讓分 | 輸注對抗點差讓分 | 和局對抗點差讓分 | 贏注⽐率 | 標準誤差 |
| 贏21分或更多 | 233 | 247 | 17 | 48.54% | 2.28% |
| 贏14-20分 | 235 | 219 | 11 | 51.76% | 2.35% |
| 贏10-13分 | 188 | 180 | 8 | 51.09% | 2.61% |
| 贏7-9分 | 198 | 181 | 12 | 52.24% | 2.57% |
| 贏4-6分 | 164 | 170 | 12 | 49.10% | 2.74% |
| 贏3分 | 202 | 212 | 14 | 48.79% | 2.46% |
| 贏2分 | 184 | 188 | 14 | 49.46% | 2.59% |
| 輸3分 | 209 | 207 | 12 | 50.24% | 2.45% |
| 輸4-6分 | 174 | 163 | 9 | 51.63% | 2.72% |
| 輸7-9分 | 187 | 195 | 9 | 48.95% | 2.56% |
| 輸10-13分 | 173 | 189 | 14 | 47.79% | 2.63% |
| 輸14-20分 | 220 | 232 | 15 | 48.67% | 2.35% |
| 輸21分或更多 | 249 | 233 | 15 | 51.66% | 2.28% |
列表是根據2000年球季週1到2010年球季週4的每⼀場NFL美式⾜球⽐ 賽。
Pinnacle運動簽賭公佈他們的概率以⼩數點的模式。我要如何將運動簽賭 概率從⼩數點模式轉換到American format美國模式?
讓我們檢視2010年⼗⽉25⽇星期⼀晚上⾜球⽐賽為例。European odds歐 洲概率公佈為:
New York Giants 2.750
Dallas Cowboys 1.513
兩個數值代表你在⼀個單位如果贏了、將會獲得的回報, 包括你原初的賭 注在內。當⼩數點的概率⼤於或等於2, 那麼轉換就很容易: 只要減去1, 接 著再乘以100. 如果概率⼩於2, 那麼(1)減去1, (2) 取其倒數, 再(3)乘 以-100.
如果你偏好使⽤公式, 若是⼩數點概率⽀付 x, 這裡是等同於美國概率的計 算:
如果 x>=2: 100*(x-1)
如果 x<2: -100/(x-1)
在以上的範例當中, 美國概率公式為:
New York Giants: 100*(2.750-1) = +175
Dallas Cowboys: -100/(1.513-1) = -195
你也可以⾃動轉換所有賭盤的概率, 利⽤選取「American Odds美國概 率」在Pinnacle網站logo上⽅、左上⾓pulldown menu拉下式選單中。
我與⼀位朋友打賭, 他⼀般是在我可以擊敗spread點差讓分50%的地⽅下 注、或者在將臨的NFL美式⾜球每⼀場正規球季。如果我贏的話, 我會拿 到$1000. 如果他贏的話, 我得⽀付$500. 直到10/31/10星期⽇我領先19場 ⽐賽、⽽他要與我deal交易妥協。這時哪⼀種提議⽐較好?
很不錯的打賭, 簡直是輕⽽易舉。這就像是丟擲硬幣拿到2⽐1的賠率。甚 ⾄更好, 因為你在tie和局也會贏。
在寫作本⽂的當時, 正規球季的256場⽐賽已經進⾏了95場。運⽤binomial distribution⼆項式分佈, 我顯⽰出你贏的機率為99.87%. 公平的議定價格 應該是$998.02.
這個問題曾被提出與討論在我的夥伴網站討論區 Wizard of Vegas拉斯維 加斯巫師.
拉斯維加斯一家體育博彩公司公佈的大學橄欖球比賽總分明顯有誤。市場數字是43,但他們開出的賠率是53。所以我押了大約20次小注,每次金額都很少,以免引起注意或影響賠率。不出所料,我贏了。現在我有點擔心要不要把賭注提交給對方付款。賭場拒絕支付是否合理?
我賭10比1你一定會贏,儘管他們可能會先跟你聊幾句。我之所以有些懷疑,是因為體育博彩公司在獲得博彩管理委員會的許可後,可以撤銷明顯錯誤的投注。
「未經主席事先書面批准,博彩公司不得單方面撤銷任何賭注。」—內華達州法規 22.115
雖然根據傳聞證據,這項權利確實存在,但很少被引用。請告訴我發生了什麼事。
P.S.:提問者後來通知我,他很順利地就拿到了報酬。
在超級盃比賽中,有一個拼字遊戲點數投注,投注的是第一個達陣得分球員姓氏對應的點數。投注額大小都是10.5和-115。哪一方比較划算呢?
我喜歡這種富有創意的投注。在博伊德賭場、棕櫚酒店、埃爾科爾特斯酒店和南角賭場都可以找到。為了回答這個問題,我查看了另一組投注,投注哪位球員率先達陣。這些賠率顯示在下表的第二列。為了簡單起見,我忽略了5-1的場地狀況,以及100-1的無達陣情況。然後,我將這些獲勝次數轉換為第三列中的“公平機率”,即投注完全公平所需的獲勝機率。由於降低了每次獲勝的賠率,這些機率被誇大了,因此總和為 166%。第四列中的「調整機率」表示公平賠率除以 1.660842,因此總機率為 100%。第五列顯示每位球員姓名對應的拼字遊戲分數。第六列中的「預期拼字遊戲分數」是機率與拼字遊戲分數的乘積。右下角單元格顯示平均拼字遊戲分數為 14.18521。
從平均值來看,高於這個數字似乎是正確的。逐一玩家統計,Scrabble遊戲中獲得11分或以上分數的機率為0.641894,換算成公平賠率則為-179。因此,-115這個高於這個數字是一個不錯的選擇。如果投注115,玩家在高於這個數字上的優勢為20%。
不幸的是,當我去下注時,賠率已經變成 -180。
拼字遊戲得分,成為超級盃中第一個達陣得分的球員
| 姓名 | 已公佈賠率 | 公平機率 | 調整機率 | 拼字遊戲總分 | 拼字遊戲預期分數 |
|---|---|---|---|---|---|
| 門登霍爾 | 4 | 0.200000 | 0.120421 | 20 | 2.408416 |
| 詹寧斯 | 4.5 | 0.181818 | 0.109473 | 22 | 2.408416 |
| 史塔克斯 | 5 | 0.166667 | 0.100351 | 10 | 1.003507 |
| 華萊士 | 7 | 0.125000 | 0.075263 | 15 | 1.128945 |
| 病房 | 8 | 0.111111 | 0.066900 | 8 | 0.535204 |
| 羅傑斯 | 8 | 0.111111 | 0.066900 | 10 | 0.669005 |
| 納爾遜 | 8 | 0.111111 | 0.066900 | 9 | 0.602104 |
| 磨坊主 | 10 | 0.090909 | 0.054737 | 11 | 0.602104 |
| 司機 | 10 | 0.090909 | 0.054737 | 11 | 0.602104 |
| 瓊斯 | 12 | 0.076923 | 0.046316 | 15 | 0.694735 |
| 羅斯利斯伯格 | 12 | 0.076923 | 0.046316 | 22 | 1.018945 |
| 桑德斯 | 15 | 0.062500 | 0.037632 | 9 | 0.338684 |
| 棕色的 | 18 | 0.052632 | 0.031690 | 12 | 0.380276 |
| 雷德曼 | 18 | 0.052632 | 0.031690 | 11 | 0.348587 |
| 誇爾斯 | 20 | 0.047619 | 0.028672 | 19 | 0.544761 |
| 庫恩 | 二十五 | 0.038462 | 0.023158 | 12 | 0.277894 |
| 傑克森 | 三十 | 0.032258 | 0.019423 | 24 | 0.466145 |
| 摩爾 | 三十 | 0.032258 | 0.019423 | 8 | 0.155382 |
| 總計 | 1.660842 | 1.000000 | 14.185214 | ||
不幸的是,當我回到賭場下注時,賠率已經變成 -180。
附註:比賽開始前幾個小時,我押了-170的賠率。可惜輸了。第一個達陣的球員是喬迪·尼爾森。尼爾森在拼字遊戲中得了9分。
在 2010-2011 賽季 NFL 比賽中,弱勢球隊在盤口差距方面表現如何?
在267場比賽中,熱門球隊128次擊敗讓分盤,冷門球隊133次獲勝,另有6場比賽平手。在已結算的投注中,冷門球隊的勝率為51.0%。
更有趣的是大小盤的勝負狀況。大盤贏了148場,小盤贏了114場,還有5場平手。在已結算的投注中,大盤的勝率為56.5%。在已結算的262場投注中,小盤贏114場或更少的機率為2.1%。
在2011年11月6日公羊隊對紅雀隊的比賽中,公羊隊在第三節拿下兩次安全分。這個機率是多少?
根據歷史經驗,每場比賽至少有一次安全得分的機率為 5.77%。
每場比賽的預期安全次數為 -ln(1-0.0577) = 0.0594。
每隊每季的預期人數為 0.0594/8 = 0.0074。
同一支球隊在單一季度中恰好有兩次安全得分的機率為 e -0.0074 ×0.0074 2 /fact(2) = 36,505 分之一。
NFL一個賽季有267場比賽,球隊有267×8=2136個賽季。所以,根據我的估計,這種情況平均每36505/2136=17.1年就會發生一次。
這應該只是一個粗略的猜測。為了簡單起見,我沒有考慮遊戲中的一些因素。
你聽過新澤西州爆米花公園動物園裡的駱駝公主的故事嗎?它在NFL讓分盤口中取得了88勝51負的戰績。它的賠率是多少?
不計入平局,在139次選擇中至少贏得88次的機率是0.00107355,也就是931分之一。這真是令人失望。我敢肯定,還有930隻動物的表現更差,只是沒人提及而已。想了解更多關於“公主”的信息,請閱讀ESPN.com上的文章《新澤西駱駝預測巨人隊戰勝愛國者隊》 。
感謝您新增的過關卡部分。我採納了您的建議,得出了以下賠率(括號中為市場點差):
- 比爾隊 +3.5 (+3)
- 充電器+7.5(+7)
- 紅雀 -2.5 (-3)
- 海豚隊 -2.5 (-3)
- 熊 +2.5 (0)
我在這次賭注中有什麼優勢?
我假設賠率是 25 比 1,這在 Golden Nugget、South Point 和 William Hill體育博彩家族的半分卡上可用。
下表顯示了您得到的線和市場價格線。
首先,弱隊贏過讓分盤的機率是51.6%。這相當於弱隊的公平賠率是-106.6。所以,你在弱隊身上贏了6.6個基點,而在強隊身上輸了6.6個基點。
其次,我提供的表格展示了在NFL中購買半分的合理價格。例如,從3分中額外獲得半分,值得投注-121.4,即21.4個基點。
下表詳細列出了您將獲得的基點數。對於熊市,我將1和2的基點數翻倍,因為如果您超過這些數字,您就能轉虧為盈。
然後,該表將總基點轉換為獲勝機率。公式為 p = (100+b)/(200+b),其中 p = 獲勝機率,b = 基點數。
最下面一行取每局勝率的乘積,得出過關投注的勝率是0.046751。賠率為25賠1,該投注的預期回報為0.046751*25-1=0.168783。換句話說,勝率高達16.9%。做得好!
Rudeboyoi 過關卡
| 團隊 | 過關投注 卡片 | 公平的 | 失敗者 基礎 積分 | 全部的 額外的 積分 | 全部的 | 可能性 |
|---|---|---|---|---|---|---|
| 帳單 | 3.5 | 3 | 6.6 | 20.8 | 27.4 | 0.560246 |
| 充電器 | 7.5 | 7 | 6.6 | 11.9 | 18.5 | 0.542334 |
| 紅雀隊 | -2.5 | -3 | -6.6 | 20.8 | 14.2 | 0.533147 |
| 海豚 | -2.5 | -3 | -6.6 | 20.8 | 14.2 | 0.533147 |
| 熊 | 2.5 | 0 | 0 | 18.0 | 18.0 | 0.541321 |
| 產品 | 0.046751 | |||||
你聽過西雅圖一家汽車經銷商因為海鷹隊完封巨人隊而賠了42萬美元的事嗎?我聽說他們為此買了7000美元的保險。那麼合理的保費是多少呢?
根據文章《 華盛頓汽車經銷商在海鷹隊完封巨人隊後賠付 420,000 美元》報道,該經銷商推出了一項促銷活動,如果海鷹隊在 2013 年 12 月 15 日舉行的第 15 週比賽中完封巨人隊,則將向 12 名獲勝者每人支付 35,000 美元。文章還說,如果真的發生了上述事件,經銷商還支付了 7,000 美元的保險費。
根據1983年至2012年賽季的每場NFL比賽,每場比賽都有特定一方完成。然而,作為一支落後7分的弱隊,在一場平均得分高於/低於的比賽中,我認為巨人隊被完封的機率高於平均水平。那場比賽的得分高於/低於41分。讓我們用一些代數運算來計算巨人隊的預期得分。
讓:
s=海鷹隊得分
g=巨人隊積分
根據點差和總分高/低,我們知道 s+g=41 和 s=g+7。
將第二個方程式代入第一個方程式:
(g+7) + g = 41
2克+7=41
2克=34
g = 17
接下來,讓我們根據1983年至2012年賽季的數據,根據每支球隊的預計得分來計算完封的機率。我跳過了樣本量為零的行。
完封機率
| 估計的 積分 | 樣本量 | 完封 | 比率 |
|---|---|---|---|
| 5.25 | 1 | 0 | 0.0% |
| 6.50 | 1 | 0 | 0.0% |
| 7.75 | 1 | 0 | 0.0% |
| 8.00 | 1 | 0 | 0.0% |
| 8.25 | 3 | 0 | 0.0% |
| 8.50 | 2 | 0 | 0.0% |
| 8.75 | 2 | 0 | 0.0% |
| 9.00 | 2 | 0 | 0.0% |
| 9.50 | 4 | 0 | 0.0% |
| 9.75 | 6 | 1 | 16.7% |
| 10.00 | 10 | 1 | 10.0% |
| 10.25 | 7 | 0 | 0.0% |
| 10.50 | 14 | 2 | 14.3% |
| 10.75 | 7 | 1 | 14.3% |
| 11.00 | 十三 | 1 | 7.7% |
| 11.25 | 21 | 1 | 4.8% |
| 11.50 | 22 | 3 | 13.6% |
| 11.75 | 23 | 1 | 4.3% |
| 12.00 | 三十四 | 2 | 5.9% |
| 12.25 | 三十六 | 7 | 19.4% |
| 12.50 | 41 | 3 | 7.3% |
| 12.75 | 三十九 | 4 | 10.3% |
| 13.00 | 55 | 1 | 1.8% |
| 13.25 | 58 | 5 | 8.6% |
| 13.50 | 78 | 1 | 1.3% |
| 13.75 | 89 | 5 | 5.6% |
| 14.00 | 92 | 4 | 4.3% |
| 14.25 | 108 | 7 | 6.5% |
| 14.50 | 117 | 8 | 6.8% |
| 14.75 | 141 | 7 | 5.0% |
| 15.00 | 160 | 7 | 4.4% |
| 15.25 | 160 | 7 | 4.4% |
| 15.50 | 213 | 7 | 3.3% |
| 15.75 | 198 | 11 | 5.6% |
| 16.00 | 206 | 6 | 2.9% |
| 16.25 | 221 | 12 | 5.4% |
| 16.50 | 241 | 10 | 4.1% |
| 16.75 | 273 | 7 | 2.6% |
| 17.00 | 306 | 8 | 2.6% |
| 17.25 | 305 | 8 | 2.6% |
| 17.50 | 306 | 10 | 3.3% |
| 17.75 | 323 | 4 | 1.2% |
| 18.00 | 299 | 8 | 2.7% |
| 18.25 | 332 | 8 | 2.4% |
| 18.50 | 309 | 9 | 2.9% |
| 18.75 | 307 | 7 | 2.3% |
| 19.00 | 356 | 8 | 2.2% |
| 19.25 | 389 | 5 | 1.3% |
| 19.50 | 361 | 5 | 1.4% |
| 19.75 | 343 | 6 | 1.7% |
| 20.00 | 402 | 8 | 2.0% |
| 20.25 | 379 | 6 | 1.6% |
| 20.50 | 359 | 3 | 0.8% |
| 20.75 | 353 | 5 | 1.4% |
| 21.00 | 344 | 1 | 0.3% |
| 21.25 | 317 | 3 | 0.9% |
| 21.50 | 341 | 2 | 0.6% |
| 21.75 | 331 | 1 | 0.3% |
| 22.00 | 369 | 1 | 0.3% |
| 22.25 | 336 | 0 | 0.0% |
| 22.50 | 316 | 2 | 0.6% |
| 22.75 | 280 | 3 | 1.1% |
| 23.00 | 311 | 1 | 0.3% |
| 23.25 | 290 | 3 | 1.0% |
| 23.50 | 279 | 1 | 0.4% |
| 23.75 | 255 | 1 | 0.4% |
| 24.00 | 246 | 1 | 0.4% |
| 24.25 | 219 | 0 | 0.0% |
| 24.50 | 230 | 2 | 0.9% |
| 24.75 | 230 | 1 | 0.4% |
| 25.00 | 212 | 2 | 0.9% |
| 25.25 | 207 | 0 | 0.0% |
| 25.50 | 176 | 1 | 0.6% |
| 25.75 | 154 | 0 | 0.0% |
| 26.00 | 154 | 1 | 0.6% |
| 26.25 | 113 | 0 | 0.0% |
| 26.50 | 137 | 0 | 0.0% |
| 26.75 | 122 | 0 | 0.0% |
| 27.00 | 95 | 0 | 0.0% |
| 27.25 | 98 | 0 | 0.0% |
| 27.50 | 83 | 0 | 0.0% |
| 27.75 | 81 | 0 | 0.0% |
| 28.00 | 82 | 0 | 0.0% |
| 28.25 | 55 | 1 | 1.8% |
| 28.50 | 56 | 0 | 0.0% |
| 28.75 | 51 | 0 | 0.0% |
| 29.00 | 四十八 | 0 | 0.0% |
| 29.25 | 三十四 | 0 | 0.0% |
| 29.50 | 24 | 0 | 0.0% |
| 29.75 | 二十五 | 0 | 0.0% |
| 30.00 | 24 | 0 | 0.0% |
| 30.25 | 21 | 0 | 0.0% |
| 30.50 | 18 | 0 | 0.0% |
| 30.75 | 23 | 0 | 0.0% |
| 31.00 | 16 | 0 | 0.0% |
| 31.25 | 15 | 0 | 0.0% |
| 31.50 | 8 | 0 | 0.0% |
| 31.75 | 3 | 0 | 0.0% |
| 32.00 | 6 | 0 | 0.0% |
| 32.25 | 7 | 0 | 0.0% |
| 32.50 | 6 | 0 | 0.0% |
| 32.75 | 3 | 0 | 0.0% |
| 33.00 | 4 | 0 | 0.0% |
| 33.25 | 6 | 0 | 0.0% |
| 33.50 | 5 | 0 | 0.0% |
| 34.75 | 4 | 0 | 0.0% |
| 35.00 | 2 | 0 | 0.0% |
| 35.50 | 1 | 0 | 0.0% |
| 36.00 | 2 | 0 | 0.0% |
| 36.25 | 1 | 0 | 0.0% |
| 36.50 | 1 | 0 | 0.0% |
| 37.25 | 1 | 0 | 0.0% |
| 37.75 | 2 | 0 | 0.0% |
| 42.25 | 1 | 0 | 0.0% |
接下來的步驟太複雜,無法在此解釋,但我根據估計的點數,開發了一個計算完封機率的公式。
p = 估計點數。
x = 1.562545 -0.302485 * p
完封機率 = e x /(1+e x )
下圖顯示了 14 至 22 分之間完封的實際機率和估計機率。
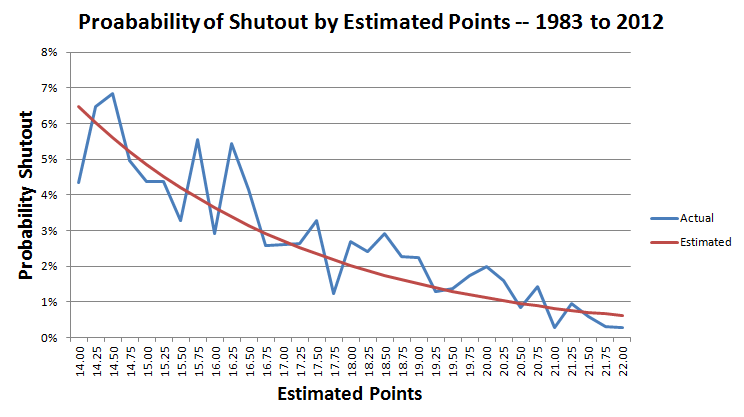
在本場比賽中巨人隊預計得分 17 分。
使用表格上方的公式:
x = 1.562545 -0.302485 * 17 = -3.579706
完封機率 = exp(-3.579706)/( exp(-3.579706)+1) = 2.71%。確切地說,是 0.0271275。
考慮到如果巨人隊完封對手,經銷商將需要支付42萬美元,那麼保單的合理成本應該是42萬美元×0.0271275=11394美元。通常情況下,承保此類特殊促銷活動的保險公司會將合理成本翻倍,所以我預計保費應在2,2788美元左右。所以,經銷商付的7000美元保費簡直是便宜。假設老闆仔細核算了一下,我可不想成為計算出這7,000美元保費的人。
這個問題是在我的「拉斯維加斯巫師」論壇中提出並討論的。
誰提供拉斯維加斯最好的期貨賠率?
根據 2015 年超級盃的期貨投注,以下是拉斯維加斯各個體育博彩集團的平均莊家優勢。
運動期貨中的莊家優勢
| 體育博彩 | 莊家優勢 |
|---|---|
| CG技術 | 21.90% |
| 威廉希爾 | 26.63% |
| 永利 | 27.96% |
| 凱撒 | 35.49% |
| 車站/埃爾科爾特斯 | 38.33% |
| 金塊 | 39.75% |
| 米高梅 | 40.88% |
| 博伊德/海岸 | 49.35% |
| 德州儀器 | 57.93% |
要計算任何一組期貨投注的平均莊家優勢,請使用我的運動期貨計算器。
我聽說Jerry's Nugget不再提供NFL讓分盤的誘人賠率了。這是真的嗎?
可惜,事實並非如此。 Jerry's Nugget 是最後一家提供 NFL 兩回合 6 分讓分盤 -110、三回合 +180 和四回合 +300 的寬容賠率的博彩公司。透過推出 Wong 讓分盤(勝負分差在 3 分和 7 分之間),這筆交易確實具有優勢。
您可以在 Wizard of Vegas.com 上我的體育博彩調查中找到拉斯維加斯周圍所有當前的聯注和讓分盤賠率。
要了解有關足球讓分盤的更多信息,請參閱我的“NFL 讓分盤投注”頁面。
在 NFL 中,在一家體育博彩公司投注超過 50 而在另一個體育博彩公司投注低於 52.5 是否是一個好的選擇?
您可以使用我在NFL中的替代總數來解答此類問題。這將顯示在總投注中獲得額外積分的機率和公平線。
假設公平的上下盤賠率是51。第一個表格顯示,假設沒有平局,投注低於52.5的獲勝機率為54.4%。第三個表格顯示,投注高於52.5的獲勝機率為53.5%。
要贏取10%的抽水,你需要有11/21 = 52.38%的勝率。這兩個投注的平均賠率是53.95%,所以,沒錯,選擇中間那個投注。你的優勢是3.0%。
在我寫這個問題的時候,NFL常規賽剛結束,Bovada給卡羅萊納黑豹隊贏得NFC冠軍的賠率是18比1。他們已經以6分領先亞利桑那黑豹隊贏得首場比賽。之後只差2分了。
難道你不認為我可以押注卡羅萊納隊贏得 NFC 冠軍,並在此過程中進行對沖,將賭注押在他們所對陣的球隊身上嗎?
不!在足球投注中,押注未來賠率和熱門球隊是最糟糕的選擇。這聽起來像是一個投注系統,把一系列負數投注加起來,然後期望總和為正。不過,我可能需要更多證據才能說服你,所以讓我們看看數據。
首先,黑豹隊之所以能進入季後賽,是因為他們是國聯南區實力最弱的球隊。他們的戰績是7勝8負,整個賽季的失分比得分高出35分。
你可能會問,如果他們實力這麼差,為什麼在對亞利桑那紅雀隊的比賽中還能領先六分呢?亞利桑那紅雀之所以能進入季後賽,很大程度上要歸功於卡森·帕爾默在前六場比賽中的出色表現。帕爾默在第六場比賽中受傷,但他們仍然勉強進入了季後賽。而且,卡羅萊納紅雀隊擁有主場優勢。
鑑於卡羅萊納隊以 6 分領先亞利桑那隊,我認為他們贏得這場比賽的機率為 70.3%。
假設他們贏了,他們很可能需要擊敗綠灣包裝工隊和西雅圖包裝工隊才能贏得NFC冠軍。擊敗這兩支球隊的機率有多大?記住,根據 季後賽規則,他們兩次都將是客隊。
有一個簡單的方法可以精確估算任何比賽的讓分。以下是我計算主隊讓分的巫師公式:
(客隊每場淨得分)-(主隊每場淨得分)-2.67。
讓我們來看看亞利桑那和綠灣之間的假設對決。
2014年賽季,卡羅萊納紅襪隊整個賽季淨勝球數為-35分。綠灣紅襪則為+138分。由於賽季共進行了16場比賽,因此將兩個數字除以16,得出平均每場比賽淨勝球數為:
卡羅萊納州:-2.1875
綠灣:+8.6250
使用我的公式,主隊綠灣的差價應該是 -2.1875 - 8.6250 - 2.67 = -13.4825。
因此,綠灣紅襪隊對卡羅萊納紅襪隊的勝率約為13.5分。我將跳過這一步的計算,但我會顯示卡羅萊納紅襪隊以13.5分的劣勢獲勝的機率為14.3%。
西雅圖的戰績與綠灣包裝工隊差不多,整個球季淨勝球數為140分。因此,卡羅萊納贏得這場比賽的機率也約為14.3%。
卡羅萊納三戰全勝的賠率是 70.3% × 14.3% × 14.3% = 1.44%。因此,基於此機率的公平期貨投注是 68.6 比 1!
是的,你可能會說底特律或達拉斯可能很幸運地進入聯盟冠軍賽。你也可能認為卡羅萊納擊敗綠灣和西雅圖的賠率呈正相關。然而,考慮到我的粗略公平賠率是68.6,而你只有18,這些都只是次要的考慮因素。
你還必須考慮在輸贏盤上押注熱門球隊的成本。這通常是一個糟糕的選擇。 Square 的投注者喜歡在輸贏盤上押注熱門球隊,進而創造價值。在輸贏盤上押注7分或以上的弱隊大致是一個公平的投注,這意味著熱門球隊的投注者要支付所有的佣金。
假設你押注亞利桑那隊+250,並在接下來的兩場比賽中以5比1的賠率獲勝。假設你押注卡羅萊納隊100美元,賠率為18比1。
首先,你押注40美元,押注亞利桑那隊,賠率為+250,作為對沖。如果他們贏了,你在這個賭注上贏了100美元,在期貨賭注上輸了100美元,最終收支平衡。
如果卡羅萊納擊敗亞利桑那,你押注700美元,贏西雅圖的140美元。如果西雅圖贏了(他們理當贏),你就能贏140美元,這能彌補你在亞利桑那和期貨投注上的損失,所以你贏了。
如果卡羅萊納爆冷,你需要下注 4,200 美元才能贏回你在亞利桑那、西雅圖和期貨投注中輸掉的 840 美元。如果卡羅萊納輸了,你就贏了。如果他們贏了,你就輸了 40 美元 + 700 美元 + 4,200 美元 = 4,940 美元。你在期貨投注中贏到的 1,800 美元不足以彌補這筆損失。
最後,你希望卡羅萊納隊贏得 NFC 冠軍並在此過程中進行對沖的想法是非常不明智的。
您對自殺池有什麼建議?
對於那些不知道的人來說,自殺式投注是一項「最後一人」的比賽,通常以NFL(美國職業橄欖球大聯盟)為藍本,不過任何運動聯盟都可以。以下是基本規則。
- 每位玩家支付相同的金額進行遊戲。
- 每週每位玩家必須預測當週一場比賽的勝負。所有比賽均以直接得分,不接受讓分。
- 一旦有選手犯錯,他就會立刻被淘汰。
- 任何球員不得多次選擇同一支球隊。
- 最後一位存活的人將贏得獎金。
可能還有其他規則,例如管理彩池的人可以分一杯羹,並且只有在雙方同意的情況下,當只剩下幾個人時,才可以平分彩池。
在進一步討論之前,以下是officefootballpool.com上賽季的比賽結果。
辦公室足球彩券-2014年賽季
| 星期 | 團隊 | 傳播 | 精選 |
|---|---|---|---|
| 1 | 菲爾 | -10.5 | 54 |
| 1 | 別緻 | -7 | 二十九 |
| 1 | 坑 | -6.5 | 14 |
| 1 | 偵探 | -6 | 6 |
| 1 | 堪薩斯城 | -3 | 5 |
| 1 | 紐約郵報 | -5.5 | 5 |
| 1 | 東北 | -4 | 1 |
| 1 | 舊金山 | -4.5 | 1 |
| 1 | 聖路易 | -3.5 | 1 |
| 2 | 登 | -12.5 | 三十八 |
| 2 | 英國 | -8 | 23 |
| 2 | 不 | -6.5 | 7 |
| 2 | 舊金山 | -7 | 5 |
| 2 | 結核病 | -5.5 | 3 |
| 2 | 洗 | -6 | 2 |
| 2 | 辛 | -5.5 | 1 |
| 2 | 東北 | -5.5 | 1 |
| 3 | 東北 | -14 | 四十四 |
| 3 | 不 | -10 | 16 |
| 3 | 亞特蘭大 | -6.5 | 3 |
| 3 | 辛 | -6.5 | 1 |
| 3 | 印度 | -6 | 1 |
| 4 | SD | -13 | 三十四 |
| 4 | 印度 | -7.5 | 20 |
| 4 | 坑 | -7.5 | 10 |
| 4 | 巴爾 | -3 | 1 |
| 5 | 不 | -10 | 21 |
| 5 | 英國 | -8 | 十三 |
| 5 | 登 | -7.5 | 6 |
| 5 | 偵探 | -6.5 | 5 |
| 5 | 菲爾 | -6.5 | 3 |
| 5 | 達爾 | -6.5 | 2 |
| 5 | 坑 | -6 | 2 |
| 5 | SD | -6.5 | 1 |
| 5 | 海 | -7 | 1 |
| 5 | 舊金山 | -5 | 1 |
| 6 | 海 | -8.5 | 21 |
| 6 | 登 | -9.5 | 十三 |
| 6 | SD | -7 | 7 |
| 6 | 辛 | -6.5 | 5 |
| 6 | 十 | -4 | 2 |
| 6 | 亞特蘭大 | -3 | 1 |
| 6 | 舊金山 | -3 | 1 |
| 7 | 東北 | -9.5 | 9 |
| 7 | 海 | -6.5 | 9 |
| 7 | 英國 | -6.5 | 3 |
| 7 | 巴爾 | -6.5 | 2 |
| 7 | 緩衝區 | -5.5 | 2 |
| 7 | 洗 | -5 | 2 |
| 7 | 達爾 | -6.5 | 1 |
| 8 | 達爾 | -9.5 | 12 |
| 8 | 堪薩斯城 | -7 | 5 |
| 8 | 克萊夫 | -7 | 1 |
| 8 | 米亞 | -6 | 1 |
| 9 | 舊金山 | -10 | 3 |
| 9 | 辛 | -10。5 | 2 |
| 9 | 海 | -14.5 | 2 |
| 10 | 巴爾 | -9.5 | 2 |
| 10 | 辛 | -6 | 1 |
| 10 | 海 | -9 | 1 |
| 11 | 英國 | -5.5 | 1 |
| 11 | 礦 | -6 | 1 |
| 11 | 不 | -7 | 1 |
| 12 | 印度 | -14 | 2 |
| 十三 | 巴爾 | -6.5 | 1 |
| 十三 | 偵探 | -7 | 1 |
| 14 | 不 | -10 | 1 |
「選擇」列指的是選擇該球隊的球員人數。
值得注意的是,從來沒有人選過弱隊。在497個選擇中,平均讓分是9.3。
我不知道他們為什麼在第 14 週記錄選秀,因為那時只剩下一名球員。
基於其他玩家行為的研究,以下是我針對自殺池的基本策略。這些只是一般指導原則,並非每週必須遵循的硬性規定。
- 記住,你的敵人是其他球員。不要太專注於預測NFL的勝負,而是專注於擊敗你的對手。
- 不要選最熱門的。大多數人都會這麼做。希望那個大熱門輸掉,這樣參賽者的數量就會大大減少。當大熱門輸掉比賽時,你應該成為倖存者,而不是受害者。
- 別忘了一條規則:你不能兩次選擇同一支球隊。話雖如此,你也不可能總是選擇強隊。有時你應該選擇實力一般的球隊,對抗實力較弱的球隊,這樣才能保住強隊輕鬆取勝的機會。
- 別費心去盤口。只需使用點差作為您贏得任何指定投注的機率指標。
- 如果一周正好有兩支熱門球隊,我會兩邊都避開。記住,你要在選擇可能獲勝的比賽和不隨波逐流之間取得平衡。一般來說,我認為選擇讓分第三高的一個是好主意,尤其是在你不想浪費一支最好的球隊的情況下。
這個問題是在我的「拉斯維加斯巫師」論壇中提出並討論的。
您對達陣後的新規則將如何影響半分聯注卡有何看法?
為了方便其他讀者,我分享一個技巧,就是利用半分過關投注中3分和7分的讓分盤口,額外獲得半分。我已經證明,這是一種可靠的優勢玩法,儘管波動性很大。
新規則將額外踢球點移回15碼線。這應該會降低踢球成功的機率,並促使更多兩分轉換嘗試。隨著兩分轉換嘗試的增多,無論成功與否,以三分或七分決出勝負的比賽應該會減少,從而降低在半分過關卡上從這些關鍵數字中獲得額外半分的價值。我們該擔心嗎?讓我們拭目以待。
首先,我們應該擔心,但這也必然是因為這個原因。其他規則的改變削弱了防守的侵略性,導致比賽得分更高。下圖顯示了1994年至2014年每個賽季的場均得分。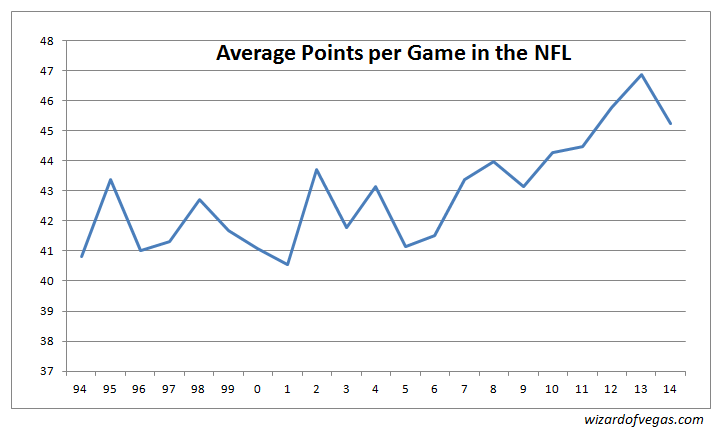
如圖所示,2006年,場均得分一直維持在42分左右。然而,從2007年開始,場均得分每年上升約半分。這引出了一個問題:平均得分的上升是否會拉平勝場分差,尤其是對於3分和7分這兩個神奇的數字。下圖顯示了各年勝場分差為3分和7分的機率。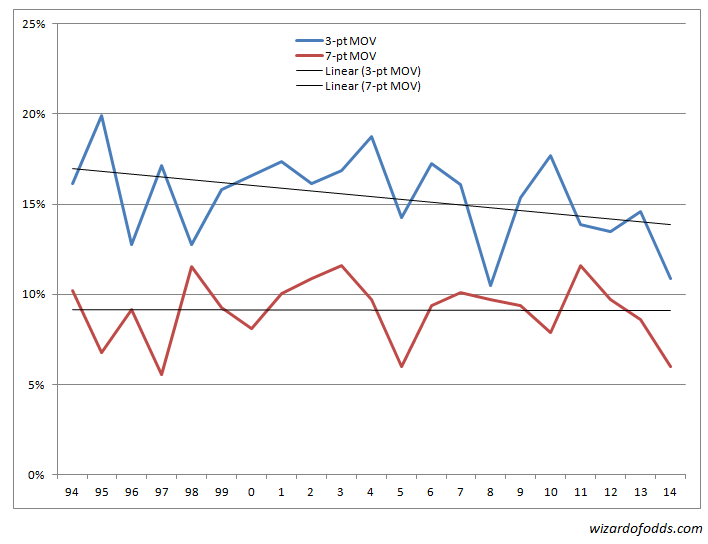
如你所見,7分淨勝的機率穩定在9.1%。然而,3分淨勝的機率一直在穩定下降,尤其是自2004年以來。這很糟糕,因為NFL中3分淨勝的情況非常普遍。
無論三分淨勝球數減少的原因是什麼,半分過關卡的價值正在下降。新的加分規則會不會讓情況變得更糟?
我的答案是,應該會造成傷害,但不會太大。在規則改變之前,我計算出大約4.8%的達陣是在兩分轉換進攻之後進行的。在我寫這篇文章的時候,規則改變之後才進行了兩週的比賽。在2015年賽季的前兩週,共有167次達陣,其中15次是在兩分轉換進攻之後進行的,達陣率為9.0%。
從數學角度來說,我認為兩分轉換應該更常見,尤其是對於那些追求差異的弱隊來說,但我不明白為什麼事實並非如此。你問的不是這個,我只是需要吐露一下。
舉個例子,假設我的讓分賠率可以持續維持在54%。為了盡快增加我的資金,哪個選項會比較划算呢?是三隊過關投注,賠率6比1嗎?
問得好。你投注11比10的優勢是3.09%,而過關投注的優勢是10.22%。這似乎為過關投注提供了一個很好的理由。
然而,請記住,任何優勢玩法下,資金成長的最佳策略都是使用凱利準則。根據凱利法則,最佳投注額是使投注後資金預期對數最大化的投注額。對於只有兩種可能結果的投注,最佳投注額恰好是優勢除以投注賠付額(以“一比一”為基準)。
直接投注賠率為10比11。因此,最佳投注額為0.030909/(10/11) = 0.034000。假設玩家優勢為3.09%,您每場直接投注的預期贏額相當於您投注本金的0.001051倍。
過關投注的最佳投注額為 0.102248/6 = 0.017041。如果玩家優勢為 0.102248,那麼你每場單註投注的預期贏取金額相當於你投注本金的 0.001742 倍。
然而,單注投注更好,因為你可以投註三次。因此,將平注投注的預期每注收益乘以三,得到 3 × 0.001051 = 0.003153。這比過關投注的資金成長高出 81%。
如果您的資金非常多,以至於達到了最高投注限額,那麼您可能應該先進行累積投注,這種投注通常不會移動線路,然後再進行直接投注。
這個問題是在我的「拉斯維加斯巫師」論壇中提出並討論的。
你知道,現在NFL附加分必須在15碼線附近嘗試,而兩分轉換球仍然在2碼線附近嘗試。你認為這會改變判決的計算方法嗎?換句話說,現在正確的打法是什麼?
這是一個邊緣判罰,我認為這也是NFL修改規則的目的。在做出決定時應該考慮以下幾點:
- 踢球成功的機率。
- 進行兩分轉換的成功機率。
- 每隊獲勝的整體機率。
在比賽後期,考慮關鍵數據也至關重要。例如,如果比賽進行到最後階段,你剛剛達陣,讓球隊領先三分,那麼你應該踢球。如果踢進,你將領先四分,迫使對方達陣才能獲勝。如果你踢進兩分,但沒踢進,對方只能透過射門得分扳平比分。所以,我將只討論比賽初期,因為那時關鍵數據並不是很重要。
為了回答你的問題,我寫了一個模擬程式。雖然程序比較粗糙,但我認為它相當準確地反映了NFL在射門得分、達陣和失誤方面的本質。
根據凱文魯迪(Kevin Rudy)的文章《將附加分移至15碼線會產生什麼影響? 》 ,從15碼線獲得附加分的機率為94.2%。為了讓數字更準確、更完整,我把這個機率設定為94%。
關於兩分轉換的機率,爭議更大。顯然,根據具體的防守和進攻,這也會有很大差異。我做的是,以46%到50%的兩分轉換成功率,以1%為一組進行模擬。
在每次模擬中,我都讓一支球隊始終踢球,而對方則在每個成功機率下嘗試轉換得分。我還進行了兩支球隊始終踢球的模擬,以便與兩分轉換得分的結果進行比較。
下表1顯示了兩支實力相當的球隊的比賽結果。 A隊總是在達陣後踢球。表格顯示了B隊獲勝的機率,以及根據B隊是踢球還是爭取兩分轉換(2PC)以及其成功機率,每場比賽平均額外得分。
表 1 — 平等團隊
| B隊 策略 | B隊 機率。 贏 | 平均 額外的 積分 |
|---|---|---|
| 踢 | 50.00% | 0.0001 |
| 2PC——46% | 49.76% | 0.0491 |
| 2PC——47% | 49.90% | 0.0000 |
| 2PC——48% | 50.05% | 0.0492 |
| 2PC——49% | 50.19% | 0.0980 |
| 2件——50% | 50.33% | 0.1461 |
請注意,成功機率為47%,無論是踢球或嘗試兩分,預期加分均為0.94。然而,嘗試兩分的獲勝機率要低0.1%。我認為這是因為如果你踢丟了,對方就有機會透過兩次射門得分扳平比分。需要注意的是,這個關鍵數字效應很小,但在其他條件相同的情況下,保守選擇踢球確實更有利。總而言之,如果兩隊實力持平,嘗試兩分轉換的成功機率至少應該達到49%。
下表2顯示了兩支實力懸殊的球隊的比賽結果,其中A隊實力更強。 A隊總是在達陣後踢球。其統計數據與上表1相同。
表 2 — 實力較強的 A 隊
| B隊 策略 | B隊 機率。 贏 | 平均 額外的 積分 |
|---|---|---|
| 踢 | 28.83% | -7.0039 |
| 2PC——46% | 29.01% | -7.0519 |
| 2PC——47% | 29.16% | -7.0039 |
| 2PC——48% | 29.30% | -6.9568 |
| 2PC——49% | 29.45% | -6.9083 |
| 2件——50% | 29.60% | -6.8595 |
表2顯示,在所有列出的成功機率下,實力較弱的球隊都應該選擇兩分轉換。即使是45%的成功機率,預期總得分也更低。你可能會問,這是為什麼?因為在任何比賽中,實力較弱的球隊都應該追求差異,而實力較強的球隊則應該厭惡差異。
下表3顯示了兩支實力懸殊的球隊的比賽結果,其中B隊實力更強。 A隊總是在達陣後踢球。其統計數據與上表1和2相同。表 3 — B 隊實力更強
| B隊 策略 | B隊 機率。 贏 | 平均 額外的 積分 |
|---|---|---|
| 踢 | 71.17% | 7.0042 |
| 2PC——46% | 70.53% | 6.9349 |
| 2PC——47% | 70.67% | 7.0030 |
| 2PC——48% | 70.82% | 7.0725 |
| 2PC——49% | 70.97% | 7.1412 |
| 2件——50% | 71.12% | 7.2109 |
請注意,表3顯示B隊透過踢球獲勝的機率為71.17%。儘管49%或50%的成功機率預期得分較高,但所有顯示的成功機率都低於這個數字。原因同樣在於,弱隊應該尋求差異,而強隊則應該避免差異。兩分轉換嘗試增加了比賽的波動性,這就是為什麼在其他條件相同的情況下,弱隊應該比強隊更傾向於嘗試這種嘗試。
卡羅萊納黑豹隊例行賽16勝0負的賠率是多少?這兩個賭注都好嗎?
是 +425 嗎?
沒有-550?
我有一種方法可以估算任何特定比賽的讓分,除非有重大傷害、康復、停賽或類似情況,否則讓分與實際讓分非常接近。以下是任何特定球隊預期得分的公式:
[(平均進攻得分) + (對手球隊平均失分)]/2 + (主場為 1.5,否則為 -1.5)。
點差為(預期客隊得分)-(預期主隊得分)。
讓我們以第13週對上聖徒隊的比賽為例。黑豹隊是客隊。本季黑豹隊場均進攻得分32.3分,聖徒場均失30.8分。根據我的公式,黑豹隊預計得分為(32.3+30.8)/2 - 1.5 = 30.05分。
然後,對聖徒隊進行同樣的計算。本季他們場均進攻得23.7分。黑豹隊場均失分18.6分。我的公式計算結果是:(23.7 + 18.6)/2 + 1.5 = 聖徒隊得分22.65分。
因此,黑豹隊預計贏30.05 - 22.65 = 7.4分。接下來,使用我的「Prop Bet Calculator」(預測投注計算器)計算每場比賽的勝率。我的計算器會計算比賽的大小分,但我發現,對於誰將直接獲勝,唯一真正重要的因素是讓分。在總分中,只要輸入本季NFL的平均分數46即可。你會發現,如果讓分是7.4,主隊獲勝的公平賠率是+271。這意味著黑豹隊的公平賠率是-271。這相當於黑豹隊的獲勝機率為271/371 = 73.05%。
然後對其他四場比賽也進行同樣的操作,並取乘積。或者你也可以直接使用下表。
黑豹隊第 13 至 17 週
| 星期 | 反對 團隊 | 地點 | 預期的 豹 積分 | 預期的 對手 積分 | 黑豹隊 獲勝 利潤 | 黑豹隊 公平的 線 | 可能性 贏 |
|---|---|---|---|---|---|---|---|
| 十三 | 聖徒 | 離開 | 30.05 | 22.65 | 7.4 | -271 | 0.730458 |
| 14 | 獵鷹隊 | 家 | 28.3 | 19.6 | 8.7 | -323 | 0.763593 |
| 15 | 巨人 | 離開 | 27.05 | 23.85 | 3.2 | -154 | 0.606299 |
| 16 | 獵鷹隊 | 離開 | 25.3 | 22.6 | 2.7 | -144 | 0.590164 |
| 17 | 海盜隊 | 家 | 30.35 | 19.05 | 11.3 | -458 | 0.820789 |
將機率列相乘,即可得出五場比賽全部獲勝的機率,即 0.163813。這對應的公平賠率是 +510。所以,你引用的兩個賠率都不太好。
這個問題是在我的 「拉斯維加斯巫師」論壇中提出並討論的。
2015 年賽季第 13 週黑豹隊與聖徒隊比賽上半場的最後一場比賽是什麼?
你可能知道,16號種子馬裡蘭大學巴爾的摩分校(UMBC)在NCAA籃球錦標賽中擊敗了1號種子弗吉尼亞大學。這在瘋狂三月34年的歷史中從未發生過。這會如何影響完美分組的機率?
在針對那場比賽以及2018賽季所有其他比賽調整了我的模型後,我得出完美分組的機率為42,743,890,552分之一。你可以在我的頁面「完美分組的機率」中了解我的策略以及我是如何得出這個數字的。
如何在美國和歐洲的表達方式之間轉換體育博彩中的賠率?
我們讓 a 成為以美國方式表達的賠率,讓 e 成為以歐洲方式表達的賠率。
從美國到歐洲:
如果a>0,則e=1+(a/100)。
如果 a<0,則 e=(a-100)/a。
從歐洲到美國:
如果e>=2,則a=100×(e-1)。
如果 e<2,則 a=100/(1-e)。
我在威廉希爾體育博彩上看到一些關於某天美國職棒大聯盟比賽是否會有大滿貫的投注。根據比賽場次,這個投注的公平機率和賠率是多少?
為了方便其他讀者,以下是2019年5月11日大滿貫賽事的賠率。列標題應為“是”和“否”,而不是“主場”和“客場”。

為了回答這個問題,我分析了2011年至2018年MLB的所有比賽。在這八個賽季中,19,440場比賽中出現了858個大滿貫。這意味著每場比賽的平均大滿貫數量為0.0441。這與任何特定比賽出現大滿貫的機率不同,因為一場比賽可能會出現多個大滿貫。使用泊松分佈,任何特定比賽至少出現一個大滿貫的機率為4.3176%。
有了這個機率,就很容易創建下表,按比賽場次顯示至少一場大滿貫賽事的機率和公平線。
大滿貫機率
| 遊戲 | 可能性 大滿貫 | 公平線 |
|---|---|---|
| 1 | 4.32% | 2216 |
| 2 | 8.45% | 1084 |
| 3 | 12.40% | 706 |
| 4 | 16.18% | 518 |
| 5 | 19.80% | 405 |
| 6 | 23.27% | 330 |
| 7 | 26.58% | 276 |
| 8 | 29.75% | 236 |
| 9 | 32.78% | 205 |
| 10 | 35.68% | 180 |
| 11 | 38.46% | 160 |
| 12 | 41.12% | 143 |
| 十三 | 43.66% | 129 |
| 14 | 46.09% | 117 |
| 15 | 48.42% | 107 |
| 16 | 50.65% | -103 |
我必須補充一點,我的答案是基於MLB的平均值。對於任何一天,玩家都應該考慮當時的特定比賽。具體來說,大小分盤口越高,贏得大滿貫的幾率就越大。
許多體育博彩公司,例如新澤西州的米高梅,都提供真正的免費投注——如果投注失敗,他們會以現金形式返還,您可以提現。這類似於老虎機的100%虧損返還,但適用於體育博彩。我應該在這個促銷活動中進行哪種投注?
像這樣的免費比賽,你絕對應該力爭上游。如果他們允許過關投注,那就盡可能多地投注過關投注,並過關投注足夠多的賽事,直到達到他們的最高賠付額,在拉斯維加斯,這個最高賠付額通常在10萬美元左右。
如果您必須對單一事件下注,那麼請找到您能找到的最大賭注。
為了說明為什麼此策略最佳,請考慮在雙零輪盤賭中下注 100 美元的相同促銷活動。如果您下注等額投注,則預期回報為 (18/38) × 200 美元 + (20/38) × 100 美元 = 147.37 美元。但是,如果您下注單一數字,則預期回報為 (1/38) × 3600 美元 + (37/38) × 100 美元 = 192.11 美元。
我在一家線上運動博彩公司看到一個促銷活動,如果NFL的輸贏盤投注中,所選球隊領先17分或以上,投注將自動計為贏家。這個活動的價值是多少?
如果所選球隊領先17分或以上後輸掉比賽,此優惠將使原本輸掉的投注變成贏利。一個很好的例子是投注第51屆超級盃亞特蘭大獵鷹隊。第三節,獵鷹隊一度以28比3領先,領先25分。然而,他們最終以34比28落敗。
為了回答這個問題,我分析了2000年至2015年NFL每個賽季的4131場比賽。下表顯示了獲胜球隊在比賽過程中的最大分差。機率列過濾掉了五場平手的比賽。
克服最大赤字
| 赤字 | 遊戲 | 可能性 |
|---|---|---|
| 領帶 | 5 | 0.000000 |
| 0 | 1804 | 0.437227 |
| 1 | 100 | 0.024237 |
| 2 | 二十九 | 0.007029 |
| 3 | 560 | 0.135725 |
| 4 | 235 | 0.056956 |
| 5 | 23 | 0.005574 |
| 6 | 131 | 0.031750 |
| 7 | 622 | 0.150751 |
| 8 | 三十九 | 0.009452 |
| 9 | 三十四 | 0.008240 |
| 10 | 195 | 0.047261 |
| 11 | 84 | 0.020359 |
| 12 | 14 | 0.003393 |
| 十三 | 49 | 0.011876 |
| 14 | 104 | 0.025206 |
| 15 | 10 | 0.002424 |
| 16 | 6 | 0.001454 |
| 17 | 三十六 | 0.008725 |
| 18 | 14 | 0.003393 |
| 19 | 2 | 0.000485 |
| 20 | 4 | 0.000969 |
| 21 | 22 | 0.005332 |
| 22 | 0 | 0.000000 |
| 23 | 2 | 0.000485 |
| 24 | 5 | 0.001212 |
| 二十五 | 1 | 0.000242 |
| 二十六 | 0 | 0.000000 |
| 二十七 | 0 | 0.000000 |
| 二十八 | 1 | 0.000242 |
| 全部的 | 4131 | 1.000000 |
「平手」這一行代表16個賽季中只有5場比賽以平手結束,所以我們不計算這些比賽。 「0」這一行代表獲胜球隊從未落後的比賽佔比為43.7%。
表格顯示,有87場比賽中,一支球隊輸掉17分或以上,然後又贏了。在已結算的4126場比賽中(即不包括5場平手),這一機率為2.11%。
考慮到這些情況會將輸贏轉化為贏,我們將這個機率乘以一,得出的數值為4.22%。輸贏盤的賭場優勢與讓分盤的賭場優勢大致相同,皆為4.76%。減去4.22%,我們得到本次促銷活動中賭場優勢非常低,僅0.54%。
2023 年瘋狂三月已經結束,您獲得完美分組和預期種子勝利的機率發生了怎樣的變化?
我制定完美分組的策略是,每場比賽都選擇種子排名較高的球隊(也就是種子號碼較低的球隊)。最後,當比賽進入1對1的局面時,隨機抽取。基於38個賽季的數據。以下是每種可能比賽的機率:
- 1號種子 vs. 16號種子 = 99.31%
- 2號種子對上15號種子=93.06%
- 3號種子對上14號種子=84.72%
- 4號種子對上13號種子=78.47%
- 5號種子對12號種子=64.58%
- 6號種子對上11號種子=62.50%
- 7號種子對上10號種子=60.42%
- 8號種子對上9號種子=51.39%
要想在第一輪生存下來,你需要贏得上面列出的八場比賽,每場四次。這個機率是1/4354。
假設您使用此策略走到這一步,以下是第 2 輪的各種對決。
- 1 比 8 種子 = 80.00%
- 2號種子對上7號種子=69.51%
- 3 比 6 種子 = 60.00%
- 4 比 5 種子 = 56.00%
要闖過第二輪,你需要贏得上面列出的四場比賽,每場四場比賽。這個機率是1/811。
假設您使用此策略走到這一步,以下是第 3 輪的各種對決。
- 1號種子對上4號種子=73.44%
- 2號種子對上3號種子=60.71%
要闖過第二輪,你需要贏得上面列出的兩場比賽各四場。機率是1/54。
第四輪將進行1號種子對上2號種子的比賽。 1號種子獲勝的機率為53.73%。這種情況發生四次的機率為0.5373÷ 4 =0.112355。
第五輪將進行兩場1對1的比賽,每場獲勝的機率為1/2,因此兩場獲勝的機率為1/4。
第六輪將進行一場1v1比賽,獲勝機率為1/2。
將所有這些機率相乘,得出完美括號的機率為 13,569,150,522 分之 1。
為了回答您的其他問題,以下是按種子排名的每支球隊的平均勝利次數。
- 1號種子=平均勝場3.29場
- 2號種子=平均勝場2.32場
- 3號種子=平均勝場數1.85
- 4號種子=平均勝場數1.55
- 5號種子=平均勝場數1.16
- 6號種子=平均勝場數1.07
- 7號種子=平均勝場0.9場
- 8號種子=平均勝場0.74
- 9號種子=平均勝場0.59
- 10號種子=平均勝場0.61
- 11號種子=平均勝場0.63
- 12號種子=平均勝場0.51
- 13號種子=平均勝場0.25
- 14號種子=平均勝場0.16
- 15號種子=平均勝場0.11
- 16號種子=平均勝場0.01


