輪盤賭 - 一般問題
更新：該賭場現已關閉。
1) 關於基本的二十一點策略，不同的線上賭場集團有不同的策略。具體來說，有兩個不同的賭場集團都使用單副牌：Microgaming 和 Unifed Gaming。我不明白為什麼你會把 11 對 10 列為 Microgaming 的熱門，而把 Unified Gaming 列為雙倍。既然他們都使用單副牌，看來這裡應該使用相同的策略。我加倍這個策略時輸的次數比贏的次數多。
2) 在輪盤賭中，我認為在紅色和第三列上投注相同金額，或者在黑色和第三列上投注相同金額，你的賠率會更高。我認為第三列有8個紅色，只有4個黑色。相反，第一列的黑色更多。這樣投注能降低賭場優勢嗎？
假設避免了可怕的五個數字組合，輪盤賭中的所有投注組合都會產生相同的預期回報。您說得對，第三列有八個紅色和四個黑色。贏得3個單位的機率是8/38，贏得1個單位的機率是4/38，不賠不贏的機率是10/38，輸掉2個單位的機率是16/38。每單位投注的預期總回報為 (1/2)*(3*8 + 1*4 + 0*10 + 2*16)/38 = -2/38。投注黑色和第三列，贏得3個單位的機率是4/38，贏得1個單位的機率是8/38，不賠不贏的機率是14/38，輸掉2個單位的機率是12/38。預期報酬為 (1/2)*(3*4 + 1*8 + 0*14 + 2*12)/38 = -2/38。兩種組合對各種結果的權重不同，但平均值相同。
哦，對了，我身後那位穿白大褂的男士想說，他很喜歡你的網站，也感謝你為了展示這些數學知識所付出的努力。他說這讓他節省了很多時間和金錢。繼續努力吧。
1000次輪盤賭獲勝
| 數位 | 可能性 |
| 0 | 0.00000000000262 |
| 1 | 0.00000000007078 |
| 2 | 0.00000000095556 |
| 3 | 0.00000000859146 |
| 4 | 0.00000005787627 |
| 5 | 0.00000031159330 |
| 6 | 0.00000139655555 |
| 全部的 | 0.00000177564555 |
所以答案是 0.00000177564555，即 563175 中的 1。我希望這種情況不會發生在網路賭場。
你可能想知道，為什麼我沒有像上面拋硬幣問題那樣使用常態近似。這是因為它在非常高和非常低的機率下都不太有效。
假設資金為b個單位，獲勝目標為g個單位，獲勝機率為p，輸掉機率為q，則您的成功機率為((q/p) b -1)/((q/p) b+g -1)。本例中，b=20，p=18/37，q=19/37，g=20、50和100。因此，對於200美元的資金，機率為((19/18) 20 -1)/((19/18) 40 -1) = 0.253252。
對於 500 美元的獲勝目標，機率為 ((19/18) 20 -1)/((19/18) 70 -1) = 0.045293。
對於獲勝目標 1,000 美元，機率為 ((19/18) 20 -1)/((19/18) 120 -1) = 0.002969。
如果球落在零上，單次禁注會怎樣？如果賭場只允許單次禁注，那麼它就會輸。然而，有些賭場允許雙次禁注，這就是會發生的情況。如果雙次禁注贏了，它會恢復為單次禁注。如果賭場只允許最多雙次禁注，那麼雙次禁注在另一個零上會輸。同樣的邏輯，如果賭場允許三次禁注，那麼雙次禁注在另一個零上會變成三次禁注。
三重監禁下的賭場優勢是1.370120%。在我解釋如何得出這個結論之前，我們先來比較單重監禁和雙重監禁。假設第一個賭注押在紅色上。
設 Z = 零的機率 = 1/37。
設 R = 紅色數字的機率 = 18/37。
單人監禁
pr（推）= ZR = 0.0131482834。
pr（勝利）= R = 0.4864864865。
pr(損失) = 1-pr(推)-pr(贏) = 0.5003652301。
預期值 = pr(贏)-pr(輸) = -0.0138787436。
雙重監禁
如果第一輪結果為零，玩家將推牌。之後，玩家可以無限次重複 ZR，直到獲得紅色。換句話說，推牌的方式如下：
ZR, Z(ZR)R, Z(ZR)(ZR)R, Z(ZR)(ZR)(ZR)R, ...
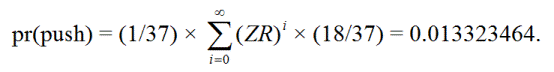
pr（推）= 0.013323464
pr（勝率）= 18/37 = 0.4864864865。
pr(損失) = 1-pr(推)-pr(贏) = 0.5001900494。
預期值 = pr(贏)-pr(輸) = -0.0137035629。
三重監禁
首先，我們來計算一下單註被禁的機率 p 1 ，即單注變成三注，加上兩個零，然後最終又升回單注。這種情況可能發生如下：
ZZRR、ZZ(RZ)RR、ZZ(RZ)(RZ)RR、ZZ(RZ)(RZ)(RZ)RR、...
換句話說，賭注可以在三倍監禁和雙倍監禁之間無限次地反覆。
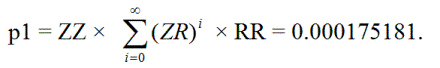
其次，設 p 2 = 單一監禁賭注達到第一級或第二級監禁，然後回到單一監禁的機率。
令 p 2 = ZR + p 1 = 0.013323464。
玩家可以無限次重複返回第一層。因此，平局的機率為：
ZR + Zp2R + Zp2p2R + Zp2p2p2R + ... =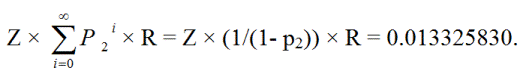
Z × (1/(1- p 2 )) × R = 0.013325830。
pr（推）= 0.013325830。
pr（勝率）= 18/37 = 0.4864864865。
pr(損失) = 1-pr(推)-pr(贏) = 0.5001876839。
預期值 = pr(贏)-pr(輸) = -0.0137011974。
無限期監禁
瑪夫，你沒問，但我聽說西班牙允許無限期監禁。設p=推擠的機率。這也是從x級監禁開始，逐級下降，最後回到x級監禁的機率。
p = ZR + ZpR + ZppR + ZpppR + ...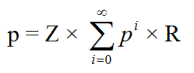
p 2 - p + ZR = 0
根據二次公式 p = (1-(1-4*RZ) 1/2 )/2 = 0.0133258620。
pr（推）= 0.0133258620。
pr（勝率）= 18/37 = 0.4864864865。
pr(損失) = 1-pr(推)-pr(贏) = 0.5001876515。
預期值 = pr(贏)-pr(輸) = -0.0137011650。
Zeros 無視監禁
最後，有些賭場會忽略第一個零之後的零，因為第一個零會限制賭注。在這種情況下，平局的機率就是 (1/37)×(1/2) = 0.0135135135。
下表總結了所有四種規則。
監禁幾率
| 監禁 | 贏 | 推 | 損失 | 預期的 價值 |
| 單身的 | 0.48648649 | 0.01314828 | 0.50036523 | -0.01387874 |
| 雙倍的 | 0.48648649 | 0.01332346 | 0.50019005 | -0.01370356 |
| 三倍 | 0.48648649 | 0.01332583 | 0.50018768 | -0.01370120 |
| 無限 | 0.48648649 | 0.01332586 | 0.50018765 | -0.01370117 |
| 忽略零 | 0.48648649 | 0.01351351 | 0.50000000 | -0.01351351 |
我要感謝 ChesterDog 和 weaselman 提供的數學協助。我還要感謝 G. Artico 教授和 polarprof.it 提供上述求和公式的 HTML 程式碼，並在此做個宣傳。
這個問題是在我的同伴網站Wizard of Vegas的論壇中提出並討論的。
輪盤上的數字順序有規律嗎？
這個想法是，輪盤應該是平衡的。換句話說，如果你取輪盤上一組連續數字的平均值，它們應該接近平均數 18.5。我想到了一種解釋雙零輪盤上數字分佈的方法，如下所示。
- 將 00 置於 12:00 位置，將 0 置於 6:00 位置。
- 輪盤頂部的數字是 13、1、00、27、10*、25。這些數字必須牢記。
- 所有低奇數（從 1 到 17）位於左側，高奇數（19 到 35）位於右側。
- 從 1 和 13 開始，逆時針移動四個位置以獲得下一個奇數，但不要超過零。
- 作為規則4的一個例外，不要將19放在17逆時針方向的四個位置，因為19的奇數較大，應該放在右邊。相反，應該放11，這是唯一一個規則4中沒有涉及的低奇數。
- 所有偶數都位於輪盤的正對面，與前一個奇數成 180 度角。
我無法解釋單零輪盤的順序。目前，我可以說，如果你把零放在12點的位置，那麼：
- 左側全是紅色的低數字和黑色的高數字。
- 右側將全部是紅色的高數字和黑色的低數字。
這個問題是在我的「拉斯維加斯巫師」論壇中提出並討論的。
我追蹤了雙零輪盤賭的3000次旋轉，因為前12個數字出現的次數似乎不如後20個數字出現的次數多。在這3000次旋轉中，1到12範圍內的數字出現了742次。這個機率是多少？
您預計球落在 1 到 12 的次數為 3000*(12/38) = 947.37。
您的結果與預期之間的差異是 947.37 - 742 = 205.37。
變異數為 3000*(12/38)*(1-(12/38)) = 648.20。
標準差是變異數的平方根 = sqrt(648.20) = 25.46。
您的結果比預期低 205.37/25.46 = 11.75 個標準差。
p 值，即偏離 11.75 個標準差或更多的機率是 28,542,806,257,940,300,000,000,000,000,000 分之一。
我很想知道輪子在哪裡。
您對本影片中介紹的 Comp Killer 輪盤賭策略有何看法？
顯而易見，該系統的目的是覆蓋大多數數字，因此這是一種風險較低的輪盤賭方式。以下是每次旋轉的投注金額：
- 3、16、24、28 和 33 日各 5 美元。
- 對以下每組數字進行角注：2/3/5/6、7/8/10/11、14/15/17/18、19/20/22/23、26/27/29/30、31/32/34/35。
請注意，這不包括以下九個數字：0、00、4、9、12、13、21、25 和 36。
下面的回報表顯示了所有可能結果的機率及其對回報的貢獻。
電腦殺手
| 事件 | 淨贏 | 組合 | 可能性 | 返回 |
|---|---|---|---|---|
| 直接獲勝 | 5 | 5 | 0.131579 | 0.657895 |
| 角球獲勝 | 50 | 24 | 0.631579 | 31.578947 |
| 所有其他 | -175 | 9 | 0.236842 | -41.447368 |
| 全部的 | 三十八 | 1.000000 | -9.210526 |
右下角單元格顯示每次旋轉的預期損失為 9.21 美元。每次旋轉的總投注額為 175 美元。因此，賭場優勢為 9.21 美元/175 美元 = 5.26%，即雙零輪盤的賭場優勢。
我想補充一點，使用這個策略，或任何輪盤策略，你輸掉的錢可能比贏回的錢還多。經驗法則是，賭場會回饋你預期損失的三分之一左右的補償。雖然有很多方法可以欺騙賭場，讓你誤以為你的預期損失比實際損失更大，但使用這個策略絕對不是其中之一。
您如何看待輪盤賭中的這種策略：
- 在黑色上投注兩個單位
- 在第三列下註一個單位
這個策略的妙處在於第三列有 8 個紅色數字和 4 個黑色數字。 16 個紅色數字中，一半位於第 1 列或第 2 列，另一半位於第 3 列。我們先忽略 0 和 00。當球落在紅色數字上時，18 個紅色數字中有 8 個位於第三列。如果中獎機率是 8/18，賠率為 2 比 1，那麼我的玩家優勢就是 33.3%。即使我們將這個數字與莊家優勢為 0% 的黑色數字投注平均，同樣先忽略 0 和 00，我的玩家優勢仍然有 16.7%。加上 0 和 00，我的玩家優勢不就是 (2/38)*-100% + (36/38)*16.7% = 10.53% 嗎？您覺得呢？
我同意，假設球落在紅色區域，忽略兩個零，第三列投注的條件優勢是33.3%。然而，按照同樣的邏輯，如果球落在黑色區域，第三列投注的勝率是4/18 = 2/9。一個勝率為2/9、賠率為2比1的投注，其莊家優勢是33.33%。所以，以你的方式來看，第三列投註一半情況下的玩家優勢為33.33%，另一半情況下的莊家優勢為33.33%。兩者相抵消，該投注的莊家優勢為0%。最後，再加上兩個零，總的玩家優勢為(2/38)*-100% + (36/38)*0% = -5.26%。
換個角度來看，下表顯示了所有可能結果的發生方式、機率、贏取的單位以及對回報的貢獻。右下角單元格顯示預期損失為 -0.105263 個單位。除以投注的 2 個單位，得出賭場優勢為 5.26%。
波希米亞策略
| 事件 | 支付 | 數位 | 可能性 | 返回 |
|---|---|---|---|---|
| 0，00 | -2 | 2 | 0.052632 | -0.105263 |
| 紅色和第 1 列或第 2 列 | -2 | 10 | 0.263158 | -0.526316 |
| 紅色和第 3 列 | 1 | 8 | 0.210526 | 0.210526 |
| 黑色和第 1 列或第 2 列 | 0 | 14 | 0.368421 | 0.000000 |
| 黑色與第 3 列 | 3 | 4 | 0.105263 | 0.315789 |
| 全部的 | 三十八 | 1.000000 | -0.105263 |
我聽說現在有四零輪盤賭了。它的莊家優勢是什麼？
是的， TCS John Huxley銷售這種輪盤。我目前還不知道具體位置。
標準輪盤的莊家優勢公式為z/(36+z)，其中z = 零的數量。本例中，莊家優勢為4/(36+4) = 4/40 = 1/10 = 10%。