概率 - 謎題
我對擲骰子機率的具體資訊很感興趣。如果你有6個骰子,一次全部擲出,那麼擲出全1的機率是46,656分之一。我的問題是,擲出1到5個1的機率是多少。我非常想知道應該用什麼公式來計算這類問題。
y 個骰子擲出 x 個 1 的機率為 combin(y,x)*(1/6) x *(5/6) yx 。請參閱我關於撲克機率的部分,以了解 combin(x,y) 函數的解釋。例如,擲出 4 個 1 的機率為 combin(6,4)*(1/6) 4 *(5/6) 2 = 0.803755%。
六顆骰子中「1」的個數
| 一 | 可能性 |
|---|---|
| 0 | 0.3348980 |
| 1 | 0.4018776 |
| 2 | 0.2009388 |
| 3 | 0.0535837 |
| 4 | 0.0080376 |
| 5 | 0.0006430 |
| 6 | 0.0000214 |
| 全部的 | 1.0000000 |
八名高爾夫球手來到一個新球場。球童主管隨機將8個球袋放在四輛球車上。球手們將8個標記的高爾夫球放入一頂帽子中。球被拋向空中。距離最近的兩個球是同伴的球袋。在所有情況下,同伴的球袋都已經放在同一輛球車上。在拋球之前,這些球袋已經正確配對的機率是多少?
組合數的公式答案為:combin(8,2)*combin(6,2)*combin(4,2)/fact(4) = 25*15*6/24 = 105。另一種計算組合數的方法是隨機選擇高爾夫球手。有7個人可以與他配對。然後從剩下的6個人中隨機選擇另一位高爾夫球手。有5個人可以與他配對。然後從剩下的4個人中隨機選擇另一位高爾夫球手。有3個人可以與他配對。所以組合數為7*5*3 = 105。因此答案為1/105。
一個朋友把這個發給了我,我想知道是否有一個公式可以解釋這個是如何運作的。
這些讀心數字謎題之所以奏效,往往是因為一個有趣的數學奇點。如果一個數字的各位數字總和能被9整除,那麼這個數字本身也能被9整除。讓我們來試試拉斯維加斯Tropicana酒店的電話號碼(702-739-2222)。各位數字和是7+0+2+7+3+9+2+2+2+2=36。36能被9整除,所以702739222也一定能被9整除。這裡有一個證明。
- 令 n 為任意整數。將 n 表示為 d 0 *1 + d 1 *10 + d 2 *100+ d 3 *1000+ ... + d n *10 n ,其中 d n是第一位數字,d n-1是第二位數字,依此類推。
- n = [d 0 + d 1 + d 2 + ... + d n ] + [d 1 *9 + d 2 *99+ d 3 *999+ ...+ d n *999...9(一個包含 n 個 9 的數字)]
- n = [d 0 + d 1 + d 2 + ... + d n ] + 9*[d 1 *1 + d 2 *11+ d 3 *111+ ... d n *111...1(一個有 n 個 1 的數字)]
- 9*任何整數都能被 9 整除。因此,如果 d 0 + d 2 + d 2 + ... + d n (或數字總和)能被 9 整除,那麼整個數字一定能被 9 整除。
現在我們已經有了證明,可以來看看這個魔術了。題目要你選一個數字。然後重新排列數字,得到第二個數字。最後用較大的數字減去較小的數字。
答案總是數字和能被 9 整除。為什麼?因為原數中的每個數字都會出現在另一個數的某個位置。每次處理一組數字,將其他所有數字都變為零,我們可以將每組數字歸結為 +/- n*[10 x - 10 y ](其中 x>=y,n 為數字)= +/-n *10 y * (10 xy - 1) = 10 y *(一個僅由 9 組成的數字)。
舉個例子。設原數為 1965,打亂後得到 6951。6951 - 1965 = 6*(1000-10) + 9*(100-100) + 5*(10-1) + 1*(1-1000) = 6*990 + 996請注意,由於每個部分都能被 9 整除,因此減法後得到的數字也一定能被 9 整除,最終各位數字之和也能被 9 整除。
然後,這個技巧會要求你圈出一個除 0 以外的數字,並輸入所有其他數字的和。程式只需在你輸入的數字上加上一個數字,使和能被 9 整除即可。例如,如果你輸入的數字和是 13,那麼你圈出來的一定是 5,因為 13 + 5 = 一個能被 9 整除的數字。
不能圈出零的原因是,如果您這樣做了,然後輸入一個已經被 9 整除的數字,那麼程式將不知道您圈出的是 0 還是 9。
很棒的網站。我經常把它比作一個對機率和統計感興趣的賭徒,但這個問題實際上與我的工作有關。我的人力資源部門堅持要求我按照鐘形曲線對我的小團隊(5人)進行評分——一個在所有員工中排名前5%,一個在其後的20%,一個在其後的50%,一個在其後的20%,還有一個在後5%。公司約有5000名員工。這麼小的樣本數符合這個分佈的機率有多大?
謝謝你的讚美。這題很好。恰好有一名員工處於最低5%的機率是5*(.05)*(.95) 4 = 0.203627。假設有一名員工處於最低5%,那麼恰好有一名員工進入接下來20%的機率是4*(.2/.95)*(.75/.95) 3 = 0.414361。假設有兩名員工處於最低5%的機率,那麼在剩下的75%中,恰好有一名員工進入接下來50%的機率是3*(.5/.75)*(.25/.75) 2 = 0.222222。剩下的兩名員工中,有一人進入25%中最低20%的機率是2*(.2/.25)*(.05/.25) = 0.32。將所有這些機率相乘,我們得到 0.006,即 1% 的 3/5。
對於提出關於順序統計量(第100列)問題的那位朋友,我有兩個小問題:一個大問題,一個小問題。你的方法沒有進行有限總體修正,我承認,對於5000名員工來說,這很容易做到,但如果只有20名員工,那肯定不行!
然而,更重要的是,你隱含地假設管理者對員工沒有影響。假設優秀的管理者透過明智的招募和解僱,或透過高於平均水準的激勵技巧,提高了員工的平均水準。如果不考慮這種影響,我們最終的機率要么向上偏向,要么向下偏向。我相信你也知道這一點,但我對此很敏感,因為我在歧視案件中做過很多類似的計算,而未能調整那些我們可以調整的因素(在本例中是特定群體的影響)常常會讓人誤入歧途。
謝謝你的這些好觀點。然而,如果無法控制工作績效評分的分配,那麼另一個選擇就是評分膨脹。經理將被迫給予過高的評分,以取悅員工。作為一名在政府部門工作了十年的公務員,我對此有一些經驗。在內華達大學拉斯維加斯分校任教時,沒有班級平均GPA標準,但對學期末的評分曲線有一定的預期。至少在大學裡,我認為這是一項合理的政策。或許在商業環境中,某種符合常識的媒介也是最好的選擇。
博彩數學家面臨哪些著名的未解難題?例如博彩界的費馬大定理。如果有,請舉個例子。
好問題。我想不出什麼。
這是如何運作的: www.1800gotjunk.com/genie/ ?
假設你的數字是 10t+u。要你減去每個數字,得到 10t+utu = 9t,這個數字能被 9 整除。請注意,所有能被 9 整除的數字都包含相同的項,也就是精靈預測的那個。
我即將參加專業執照考試。規定如下:
- 考試共設7科。
- 每科將有 60 題選擇題。
- 每道選擇題應有四個可能的答案,但只有一個正確答案。
- 為了通過考試,考生必須獲得至少 75% 的總平均成績,且任何科目的成績不得低於 65%。
我的問題是,如果考生所有答案都靠猜,他通過考試的機率有多大?換句話說,純粹靠運氣通過考試的機率有多大?
要滿足75%的正確率,考生必須在420題中至少答對315道。猜測的正確答案預期數量為420*0.25=105道。標準差為(420*0.25*0.75)^0.5 = 8.87412。因此,考生必須超出預期210題,即210/8.87412=23.66432個標準差。做到這一點的機率高得離譜。如果地球上的每個人都參加這項測試,隨機作答,我懷疑沒有人或任何東西能通過。我什至不想討論另一個要求。
如果⼀所⼤學的⾜球隊贏得⽐賽1的機會是10%、贏得⽐賽2的機會是 30%、兩場⽐賽皆輸的機會是65%, 他們剛好贏到⼀場⽐賽的機會是多 少?
如果我們假設⽐賽都是各⾃獨⽴的, 那麼輸掉兩場⽐賽的機率將是 90%*70%=63%. 不過既然你說輸掉兩場⽐賽的機率實際上為65%(這⽐起 63%還要⾼), 也就是說兩場⽐賽是相關的。如果輸掉兩場⽐賽的機率是 65%、只輸掉⽐賽2的機率是70%, 那麼贏得⽐賽1並且輸掉⽐賽2的機率 必須是5%. 運⽤相同的邏輯、輸掉⽐賽1並且贏得⽐賽2的機率必須是 25%. 這樣贏得兩場⽐賽的機率只剩下5%. 所以剛好贏得⼀場⽐賽的機率 為 25%+5% = 30%.
在遊戲節目《讓我們來做個交易》中,有三扇門。舉例來說,假設兩扇門後是山羊,一扇門後是一輛新車。主持人蒙提·霍爾挑選了兩位參賽者來選擇一扇門。每次蒙提都會先打開一扇門,展示門後的山羊。假設這次打開的是第一位參賽者選擇的門。雖然蒙提實際上從未這樣做過,但如果此時他給另一位參賽者一個機會,可以換到另一扇未開啟的門,這位參賽者應該換嗎?
是的!這個問題的關鍵在於主持人注定會打開一扇有山羊的門。他知道哪扇門後有汽車,因此無論玩家選擇哪扇門,他總能先揭示一隻山羊。這個問題被稱為「蒙提霍爾悖論」。之所以會產生許多困惑,往往是因為在問題描述時,未能明確說明主持人知道汽車的位置,並且總是先揭示一隻山羊。我認為這部分責任要歸咎於瑪麗蓮·沃斯·莎凡特,她在專欄中對問題的描述不佳。假設獎品在1號門後,以下是玩家(第二位參賽者)採取不換門策略時會發生的情況。
- 玩家選擇了門1 --> 玩家勝利
- 玩家選擇了門2 --> 玩家輸了
- 玩家選擇了門3 --> 玩家輸了
若玩家採取換門策略,將會發生以下情況。
- 玩家選擇了門1 --> 主持人揭示門2或門3後的山羊 --> 玩家切換到另一扇門 --> 玩家失敗
- 玩家選擇了門2 --> 主持人揭露了門後的山羊在第三扇門 --> 玩家轉換到門1 --> 玩家勝利
- 玩家選擇了門3 --> 主持人揭露了門2後面的山羊 --> 玩家轉換到門1 --> 玩家勝利
因此,不換門的話,玩家有1/3的獲勝機會。而選擇換門,玩家的獲勝機會則提升至2/3。所以玩家絕對應該選擇換門。
若要進一步了解蒙提霍爾悖論,推薦閱讀維基百科上的相關文章。
我不同意你在2004年11月19日專欄中對蒙提霍爾問題的回答。假設汽車在1號門後面,獎品在1號門後面,那麼實際上有以下四種可能性。
- 玩家選擇門 1 --> 顯示 2 --> 切換到 3,輸
- 玩家選擇門 1 --> 顯示 3 --> 切換到 2,輸
- 玩家選擇門 2 --> 顯示 3 --> 切換到 1,獲勝
- 玩家選擇門 3 --> 顯示 2 --> 切換到 1,獲勝
如你所見,無論你換不換,獲勝的機率都是50%。而且,認為換個比較好,這完全違背常識。
你的錯誤在於假設每個事件都有25%的可能性。以下是每個事件的正確機率。
- 玩家選擇門 1 (1/3) * 顯示門 2 (1/2) = 玩家輸 (1/6)
- 玩家選擇門 1 (1/3) * 顯示 3 (1/2) = 玩家輸 (1/6)
- 玩家選擇門 2 (1/3) * 顯示 3 (1/1) = 玩家獲勝 (1/3)
- 玩家選擇門 3 (1/3) * 顯示 2 (1/1) = 玩家獲勝 (1/3)
因此失敗事件的總機率為 2*(1/6) = 1/3,獲勝事件的總機率為 2*(1/3)=2/3。
有五種不同的配料可供選擇,您可以製作多少種不同的披薩,以及多少種配料?
有 1 種做法,0 種配料;5 種做法,1 種配料;10 種做法,2 種配料;10 種做法,3 種配料;5 種做法,4 種配料;還有 1 種做法,5 種配料。所以答案是 1+5+10+10+5+1 = 32。另一種解法是,可以加配料,也可以不加裝。所以總數是 2 +5 = 32。
我上週在報紙上看到,印尼最近一次遭受破壞的地震發生在12月26日。報紙也顯示,在過去100年發生的八次最致命的地震中,有三次發生在12月26日。我想知道,考慮到以下事實,同一天發生三次大地震的機率有多大:這種震級(8.0級或更大)的地震每年只發生一次。上一次大地震剛好發生在一年前,2003年12月26日,發生在伊朗(連續發生的機率?)。期待您的回覆。
在發現佛羅裡達颶風只襲擊布希選區縣的說法純屬騙局(參見2004年10月17日專欄)後,我對這種所謂的巧合更加懷疑了。根據美國國家地震資訊中心的數據,自1990年以來發生的11次最大地震中,只有最近的一次發生在2004年12月26日。你提到的伊朗地震只有6.7級,遠遠沒有進入前八名。
如果你每天賣出一半雞蛋,再加上半顆雞蛋,那麼一開始你有多少個雞蛋?三天後,雞蛋數量為零。每天結束時,雞蛋數量都是整數。
設d(代表白天)表示一天開始時雞蛋的數量,n(代表夜晚)表示一天結束時雞蛋的數量。問題告訴我們d/2 - ? = n。那麼,我們用n來解d。
d/2 = n + ?
d=2n+1
所以第三天 n=0,所以 d=1。
第二天n=1,所以d=3。
第三天n=3,所以d=7。
所以,你一開始就有 7 顆雞蛋。
想像一下,一個島上居住著10個人,島上的政策是這樣的:每天隨機選出一名島民擔任酋長,任期恰好一天;一天過去後,再隨機選出另一名島民(因此,剛剛擔任酋長的島民再次擔任酋長的概率為1/10)。需要解決的問題是:平均而言,每個島民至少擔任一次酋長需要多少天?
只要1天就能選出1人擔任酋長。第二天出現新酋長的機率為0.9。如果每天的機率為0.9,則產生新酋長的預期天數為1/0.9 = 1.11。這對於任何機率都成立:成功的預期嘗試次數為1/p。因此,在2人擔任酋長後,第二天出現新酋長的機率為0.8。因此,等待第三位酋長的時間為1/0.8 = 1.25天。答案是等待時間的總和,即1/1 + 1/.9 + 1/.8 + ... + 1/.1 = 29.28968天。
圓的半徑為1。三角形是等邊三角形。求每個顏色區域的面積。
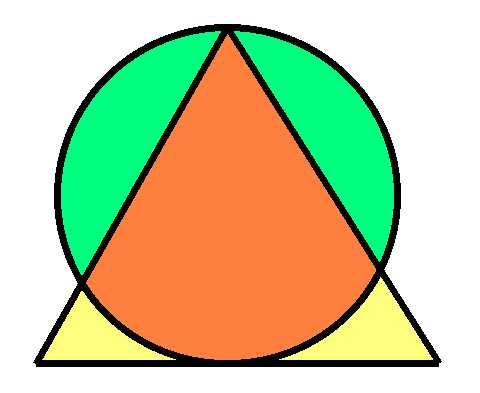
我不想把答案透露給那些想自己解決的人。想要取得答案和解答,請造訪我的另一個網站mathproblems.info ,問題 189。
假設你贏了一場比賽,在一場NBA比賽中場休息時,你有機會罰球,如果你罰中,你將贏得100萬美元。此外,你可以繼續罰球,雙罰或不罰,直到罰球不中或選擇停止。如果你的罰球命中率是75%,你會在什麼時候停下來?你會停下來嗎?到了某個時候,金錢對你來說變得越來越不重要了。你會怎麼做?
在某些時候,你應該拒絕一個好的賭注,因為賭注太高了。我個人認為衡量一個人從金錢中獲得的快樂程度的一個好方法是對金額取對數。對數的底數並不重要,所以我們使用 10。但是我們不能取小於 10 的對數,所以我們假設對於小於 10 的任何金額,快樂程度都是 0。所以在你的例子中,我們假設你在第一次罰球贏得 1,000,000 美元之前擁有 0 美元。現在你有 log(1,000,000) = 6 個單位的快樂。你再次罰球的快樂預期值是 0.75*log(2,000,000) + 0.25*0 = 4.975772。這小於 6,所以在這種情況下你應該拿走一百萬美元然後走開。但是如果你已經有一些錢,情況可能會有所不同。假設你已經有 20 萬美元。那麼,你放棄下注的幸福感是 log(1,200,000) = 6.07918。你冒著百萬風險再賭一把的幸福感是 0.75*log(2,200,000) + 0.25*log(200,000) = 6.082075,所以你勉強選擇第二次。如果你贏了那一次,你的選擇將是 log(2,200,000) = 6.34242 和 0.75*log(4,200,000) + 0.25*log(200,000) = 6.29269 之間。在這種情況下,你不應該再賭第三次,而是選擇放棄這 2,000,000 美元的獎金。接受第一次雙倍下注的損益平衡點是現有財富 191,487 美元。要接受兩次雙倍下注,你需要有 382,975 美元的其他資金。
我記得如果一個房間裡有22個人,那麼有兩個人過同一天生日(月份和日期,而不是年份)的機率是相等的。我忘了怎麼算才能證明這一點了。請問您能提供一下嗎?
我想我之前回答過這個問題,但 50/50 的機率更接近 23。為了簡單起見,我們忽略閏年。詳細答案是,以某種方式對這 23 個人進行排序。 2 號人生日與 1 號生日不同的機率是 364/365。假設 1 號和 2 號生日不同,那麼 3 號生日與 1 號和 2 號生日不同的機率是 363/365。如此反复,直到 23 號人。因此,機率為 (364/365)*(363/365)*...*(343/365) = 49.2703%。因此,不匹配的機率為 49.27%,至少匹配一個的機率為 50.73%。 Another solution is the number of permutations of 23 different birthdays divided by the total number of ways to pick 23 random numbers from 1 to 365, which is permut (365,23)/365 23 = 42,200,819,302,092,400,000,000,000,000,000,000,000,000,000,000,000,000,000,000 / 85,651,679,353,150,300,000,000,000,000,000,000,000,000,000,000,000,000,000,000 = 49.27%.
某州教師的周薪呈常態分佈,平均數為490美元,標準差為45美元。隨機抽出一位教師,週薪超過525美元的機率是多少?我不記得如何只根據平均值和標準差,而不考慮總體數據來計算機率。
這意味著價格高於平均35美元,或7/9個標準差。高於預期7/9個標準差以上的機率為1-Z(7/9) = 1- 0.78165 = 0.21835。
兩個人正在玩石頭剪刀布。假設這個遊戲不涉及策略。如果玩的是“三局兩勝制”,玩家A贏得第一輪,那麼玩家B獲勝的機率是多少?
玩家 B 需要贏得接下來的兩場比賽(不包括平手),因此機率為 (1/2)*(1/2) = 1/4。
你好,我想問你這個問題,因為我在網路上找不到。希望你能回答我的問題:存在的可能性有多大?無論是在地球上還是在宇宙的其他地方?這不是賭博問題,而是我們都應該知道的答案,這樣我們才能體會到,活著究竟能克服多少困難!
我認為銀河系中任何地方存在智慧生命的可能性都非常高。德雷克方程式試圖估算銀河系中智慧生命的數量,根據輸入的數字,得出的數字大約是一百萬。然而,也沒有確切的證據顯示這些文明曾經造訪過我們或與我們接觸。所以著名的費米問題是「他們都在哪裡?」我確實認為缺乏其他智慧生命存在的證據對德雷克方程式產生了一些懷疑,但我仍然認為我們銀河系中智慧文明的數量大約在1000個左右。這還只是我們銀河系,外面還有數十億個星系。然而,星系之間的距離如此之大,討論它們之間的旅行或交流真的沒有多大意義。所以回答你的問題,我認為大約是99.9%。
假設一家旅館有 10,000,000 個房間,電子鑰匙數量為 10,000,000 把。由於電腦出錯,每把鑰匙都被編入一個隨機密碼,正確率只有 1/10,000,000。酒店房間已滿。至少有一位顧客持有可用鑰匙的機率是多少?
精確答案:1-(9,999,999/10,000,000) 10,000,000 = 0.632121。這與 (e-1)/e 精確到小數點後七位相同。
考試中有75道選擇題。每題有4個可能的答案,只有1個正確。考試的及格分數是50%。猜對每個答案通過考試的機率是多少?
635,241 分之 1。
對於賽中投注,如果一名網球運動員贏得一場比賽的機率為“p”,那麼他贏得一盤比賽的機率是多少?
據我理解,網球規則規定,一盤比賽的勝者是率先贏得六局,且淨勝至少兩局的一方。 6-6平局將進行一局決勝。下表顯示了在已知勝局機率的情況下,贏得一盤比賽的機率。
網球中的機率
| 可能性 遊戲勝利 | 可能性 盤勝 |
| 0.05 | 0.000003 |
| 0.1 | 0.000189 |
| 0.15 | 0.001899 |
| 0.2 | 0.009117 |
| 0.25 | 0.028853 |
| 0.3 | 0.06958 |
| 0.35 | 0.138203 |
| 0.4 | 0.23687 |
| 0.45 | 0.361085 |
| 0.5 | 0.5 |
| 0.55 | 0.638915 |
| 0.6 | 0.76313 |
| 0.65 | 0.861797 |
| 0.7 | 0.93042 |
| 0.75 | 0.971147 |
| 0.8 | 0.990883 |
| 0.85 | 0.998101 |
| 0.9 | 0.999811 |
| 0.95 | 0.999997 |
贏得遊戲 p 和輸掉 q 的機率公式為 1*p 6 + 6*p 6 *q + 21*p 6 *q 2 + 56*p 6 *q 3 + 126*p 6 *q 4 + 252*p 7 *q 5 + 504*p 7 *q 6
你在一個淡水湖上,搭著船,船上有一塊石頭。你把石頭丟進湖裡。相對於陸地(岸邊),湖水位是上升、下降還是不變?我的同事認為水位會維持不變。
相對於岸邊的水位將會下降。在船內,岩石向下壓著獨木舟,從而將周圍的水向上推。排開的水量等於岩石的重量。例如,一塊10磅重的岩石將向上排開10磅的水。當岩石被拋到海裡時,重量不再重要,重要的是岩石的體積。因此,岩石將向上推開與其體積相等的水。岩石的質量大於水的質量,因此岩石向下排開的水比岩石本身排開的水更多。因此,當岩石在獨木舟中時,湖面水位將高於湖底。
這是如何運作的?
- 拿一個計算機。 (你無法在腦子裡做這件事)
- 輸入您的電話號碼的前三位數字(不是區號)
- 乘以 80
- 加 1
- 乘以 250
- 添加您的電話號碼的後 4 位數字
- 再次新增您的電話號碼的最後 4 位數字。
- 減去250
- 將數字除以 2
你認得答案嗎?
假設你的電話號碼的前三位數字為 x,後四位數字為 y。現在看看每一步的結果。
- 準備好!
- 十
- 80倍
- 80x+1
- 250*(80x+1) = 20000x+250
- 20000x+250+y
- 20000x+250+2y
- 20000x+250+2y-250 = 20000x+2y
- (20000x+2y)/2 = 10000x+y
所以這當然等於你的電話號碼。我們需要 10000x 將前綴向左移動四位,然後加上最後四位數字。
有一場價值 27,000 美元的汽車抽獎,彩券售價為六張 500 美元,或一張 100 美元。目前已售出 68 張彩票,明天是購買截止日期。我知道,要達到 50% 的中獎機率,我必須花費 5666.44 美元;要達到 66.66% 的中獎機率,我必須花費 11,332.88 美元(對嗎?)。我應該花多少錢(或者說我必須買多少張彩票)才能確保我「贏得」這輛車? (90%?95%?)這個抽獎活動值得參加嗎?還是我必須花掉買車的錢?
關於1/2和2/3的機率,你的說法是對的。如果你買了t張彩票,你的中獎機率是t/(68+t)。所以,對於90%的機率,t的解法如下。
0.9 = t/(68+t)
0.9*(68+t) = t
61.2 = 0.1噸
t = 612,即 51,000 美元
對於 95% 來說...
0.95=t/(68+t)
0.95(68+t) = t
64.6 = 0.05噸
t = 1292,或 107,666.67 美元
假設這輛車對你來說價值 27,000 美元,那麼一旦售出的下一張彩票不能增加你中獎的機率以保證其價值,你就應該停止購買彩票。
為了使彩票物有所值,它應該會將您中獎的機率提高 p,其中...
27000*p=(500/6)
p=0.003086
假設您購買了 t 張票,但您並不想再買一張票。
[(t+1)/(t+68+1)] − [t/(t+68)] = 0.003086
[(t+1)/(t+69)] − [t/(t+68)] = 0.003086
[((t+1)*(t+68))/((t+69)*(t+68))] − [(t*(t+69))/((t+68)*(t+69))] = 0.003086
[(( t2 +69t+68)/((t+69)*(t+68))] − [( t2 +69t)/((t+68)*(t+69))] = 0.003086
68/((t+68)*(t+69)) = 0.003086
((t+68)*(t+69)) = 220.32
t2 +137t+4692=22032
t2 +137t-17340=0
t=(-137+/-(137 2 -4*1*-17340) 2 )/2
t = 79.9326
讓我們透過插入一些購買門票的價值來測試這一點,假設玩家總是可以以每張 500 美元/6 = 83.33 美元的價格購買門票。
如果有 79 張彩票,您的成本為 79*(500/6) = 6,583.33 美元,您中獎的機率為 79/(79+68) = 53.74%,您的預期回報為 27,000 美元*0.5374 = 14,510. 6,583.33 美元 = 7,926.87 美元。
80 張彩券的成本為 80*(500/6) = 6,666.67 美元,中獎機率為 80/(80+68) = 54.04%,預期回報為 27,000 美元*0.5405 = 14,594.596 美元,預期利潤為 174. 7,927.92 美元
81 張彩券的成本為 81*(500/6) = 6,750.00 美元,中獎機率為 81/(81+68) = 54.36%,預期回報為 27,000 美元*0.5436 = 14,677.85 美元,預期利潤為 109. 7,927.85 美元。
因此我們可以看到,最大預期贏利額在 80 張票時達到高峰。
我正在嘗試比較現在更換舊冰箱以節省電費與等到它壞了再更換的成本。我可以計算出新冰箱比舊冰箱便宜多少:每年 37 美元,這很容易。但是我該如何計算新冰箱的成本呢?假設新冰箱的價格為 425 美元。我不能說這 425 美元*全部*都是新的支出,因為我*總有一天*要更換舊冰箱,如果不是現在的話,所以無論如何我遲早都會有這筆新冰箱的費用。假設一台普通冰箱的使用壽命為 14 年,而我的舊冰箱已經用了 9 年,所以如果我現在更換它,那麼 5 年後就需要更換它了。我嘗試製作一個兩列表格,比較使用現有冰箱9年後更換的成本和現在更換的成本,但我不知道如何進行同類比較,因為我不知道要考慮未來多久的成本,而且冰箱的更換年份也不同。我該如何比較現在更換和以後更換的經濟性?順便說一句,這不是針對我自己的情況,因為我現在的冰箱大概已經用了30年了。這是買給一個朋友的。
如果您繼續使用現有的冰箱,那麼五年後,與購買新冰箱相比,您將多花 37 美元*5 = 185 美元的電費。如果您現在更換冰箱,您將損失 425 美元,但假設五年後仍按線性折舊計算,其價值仍為 425 美元*(9/14) = 273.21 美元。因此,您將因折舊而損失 425 美元*(5/14) = 151.79 美元。因此,新冰箱的折舊成本低於保留舊冰箱的額外電費,所以我建議現在就購買新冰箱。
如果有三個人,那麼至少有兩個人的生日是同一天的機率是多少。
忽略閏日,三個生日不同的機率為 (364/365)*(363/365) = 0.99179583。因此,至少有一個生日相同的機率為 1 - 0.99179583 = 0.00820417。
一個房間裡有五個人。其中至少有兩個人出生在同一月份的機率是多少?
為了簡單起見,我們假設每個人出生在不同月份的機率為 1/12。五個人出生在不同月份的機率為 (11/12)*(10/12)*(9/12)*(8/12) = 0.381944。因此,五個人出生在同一月份的機率為 1 - 0.381944 = 0.618056。
我們在工作上遇到了一個難題——純粹為了好玩,結果誰也想不出來。一位農民有五輛拖車,裝滿了羊。其中四輛拖車的羊重39公斤,第五輛拖車的羊重40公斤。所有的羊都長得一模一樣。他去市場,想找出哪一輛拖車裡的羊重40公斤,而他只能用一次大秤! ! !他是怎麼做到的?請幫忙,我工作的地方快把我們都逼瘋了──這可是獸醫診所啊! !
答案就在專欄的最後。
回答羊的問題
從拖車 1 中取出一隻羊,從拖車 2 中取出兩隻,從拖車 3 中取出三隻,從拖車 4 中取出四隻,從拖車 5 中取出零隻。如果所有羊的重量為 39 公斤,則總重量為 39 * 10 = 390 公斤。然而,0 到 4 隻羊的重量會比 1 公斤重。如果總重量為 391,那麼秤上有一隻較重的羊;因此它一定來自拖車 1。同樣,如果總重量為 392,那麼秤上有兩隻較重的羊,它們一定來自拖車 2。同樣,重量為 393 表示較重的羊在拖車 3 中,重量為 394 表示較重的羊在拖車 4 中,重量為 390 表示較重的羊在拖車 5 中。
在一架有 180 個座位的飛機上,我坐在與我所看到的同一航班的漂亮女孩旁邊的機率有多大?
這取決於座位集群的數量。大多數國內航班走道兩側各有三個座位。這樣一來,就有60個三座集群。你們中第一個人就座後,剩下的179個座位中,會有兩個座位位於同一集群,所以位於同一集群的機率是2/179 = 1.12%。那麼,中間座位就不可能有其他人了。第三個人坐在中間座位的機率是1/3。所以答案是(2/179)*(2/3) = 0.74%,也就是1/134.25。
三位邏輯學家正在玩一個遊戲。每個人都必須秘密寫下一個正整數。寫出最小唯一整數的邏輯學家將贏得3美元。如果三位邏輯學家都寫下相同的數字,則每人將贏得1美元。這三位邏輯學家都很自私,都想最大化自己的獎金。遊戲不允許交流。那麼,每位邏輯學家會採取什麼策略呢?
答案將會出現在下一欄。
我讀到一篇報道,華倫‧巴菲特(世界第三大富豪)抱怨說,他只繳17.7%的聯邦稅,而他的秘書卻繳了30%。我覺得這太離譜了。你能評論一下嗎?
通常我會說這超出我的專業範圍。然而,身為一名在政府部門工作了八年的精算師,我對稅收略知一二。據我所知,華倫·巴菲特的大部分收入被定義為資本利得,稅率僅15%。不管你喜不喜歡,稅法允許這樣做。讓我感到困惑的是,為什麼他的秘書要繳高達30%的稅。根據這段視頻,他計算的是“工資稅和所得稅”。他所說的「工資稅」顯然是指社會安全稅和醫療保險稅。讓我們看看30%對他的秘書來說是否是一個合理的聯邦總稅率。
2007 年最高稅率為 35%,但這只適用於 349,700 美元以上的收入。該點之前的收入稅要少得多。假設他的秘書是單身,沒有受扶養子女,她的薪水為 10 萬美元。首先,我們減去最低扣除額。 2007 年單身申報者的標準扣除額為 5,350 美元。個人扣除額為 3,400 美元。因此,我們還剩下 100,000 美元 - 5,350 美元 - 3,400 美元 = 91,250 美元的應納稅收入。對於 2007 年的單身申報者,收入的前 7,825 美元稅率為 10%,然後是 15% 至 31,850 美元,然後是 25% 至 77,100美元,因此,她的所得稅應為:0.1×7,825美元+0.15×(31,850美元-7,825美元)+0.25×(77,100美元-31,850美元)+0.28×(91,250美元-77,1000 美元) = 175美元。這僅佔她收入的19.7%。我所有的假設,例如她的收入、報稅身分以及不逐項申報,都對她不利,或者說,她的稅率更高。
現在我們來算是社會安全和醫療保險。 2007年,社會安全稅為6.2%,最高可達97,500美元,之後就完全取消了。 2007年的醫療保險稅率為1.45%,沒有上限。所以,她的社會安全稅和醫療保險稅總計為6.2%*97,500美元+1.45%*100,000美元=7,495美元。算上這些稅款,她的總稅率為(19,660.75美元+7,495美元)/100,000美元=27.2%。但距離30%的目標仍差2.8%。
我猜她可能也考慮到了最終是她要為雇主支付相應的社會安全和醫療保險稅。對於那些不知道的人來說,社會安全和醫療保險稅實際上是從你的支票中扣除的兩倍。雇主支付另一半。然而,包括我在內的一些人認為最終是僱員要支付這兩項費用。如果雇主不必繳那項稅,他就有更多的錢支付員工薪水。當你像我一樣是自僱人士,必須支付這兩部分費用時,很容易有這種感覺。如果你將社會安全/醫療保險稅翻倍,稅率現在是(19,660.75 美元 + 2×7,495 美元)/100,000 美元 = 34.7%。我猜這 4.7% 的差額是因為她賺得不到 10 萬美元、已婚、有受扶養人、逐項列出扣除額或以上幾種情況的綜合作用。
社會安全稅和醫療保險稅對華倫·巴菲特來說影響不大。首先,97,500 美元的社會安全上限對他來說微不足道。其次,這些稅適用於工資,而不是資本利得,因為他將大部分的收入定義為資本利得。
所以,這是我對巴菲特先生言論背後的數學原理的最佳猜測。
更新:這篇專欄文章發表後不久,我收到了以下回應。為了公平起見,我提出以下論點:巴菲特先生繳納的稅金過多。
我饒有興趣地讀了你對那位「憤怒」人士的回答,他覺得華倫‧巴菲特繳納的稅金比例比他的秘書還低,這太不公平了。我對你的回答感到失望,因為它沒有糾正暗示巴菲特繳納的稅款比他的秘書還少的錯誤訊息。首先,正如您所說,投資收入確實要以15%的稅率徵稅。這其實是雙重課稅,因為巴菲特先生投資的勞動所得是依照他36%的邊際稅率課稅的。這就像是蘋果和橘子(工作收入和投資收入)的比較。
其次,不應該只看百分比。用賭博的用語來說,應該看「賠付」。我非常肯定,巴菲特先生當年繳了數百萬美元的稅款,而他的秘書只繳了數千美元。你的讀者不應該更憤怒嗎?一個國家公民為同樣的政府服務繳納的稅款比其他公民高出數千倍?人們完全可以毫不猶豫地說:“我聽說沃倫·巴菲特繳納的稅款比他的秘書多一百萬倍,這太離譜了!”
我只是想指出,只看“百分比”而不看“實際賠付”是謬論。這跟你很多賭博謬論類似。
此致,
凱文A.(達拉斯)
感謝您收集的這些有趣的數學謎題。我和我的女朋友想出了這個海盜謎題的變體。如果所有海盜的等級相同,並且每回合都透過抽籤決定分配方案的提議者,會怎麼樣?在這個變種中,假設每個海盜的首要任務是最大化他預期獲得的金幣數量。我找到了我認為的答案,但也許你想先嘗試一下。再次感謝。
不用客氣。如果只剩下兩個海盜,那麼被選中提出建議的那個海盜就沒希望了,因為另一個海盜會投反對票。被抽中的那個海盜會得到零分,另一個海盜則會得到全部1000分。所以,在抽籤之前,剩下兩個海盜的預期價值是500個硬幣。
在三海盜階段,抽到的海盜應該建議給其他海盜中的一位501,給自己499。抽到501的海盜會投贊成票,因為它比投反對票的預期值500還要高。抽獎前,剩下三位海盜,你分別有1/3的機率得到0、499或501枚硬幣,平均333.33枚。
在四海盜階段,抽到的海盜應該選擇將 334 枚硬幣給其他任兩名海盜,並給自己 332 枚。這樣一來,他就能從獲得 334 枚硬幣的海盜那裡獲得兩票“贊成”,因為他們寧願要 334 枚硬幣,也不願要 333.33 枚。算上你自己的一票,你將獲得 4 票中的 3 票。抽籤前,每位海盜的期望值是 0、334、334 和 332 的平均值,即 1000/4=250。
依照同樣的邏輯,在五個海盜的階段,抽到的海盜應該選擇給任兩個海盜251,給自己498。與原題不同,這裡不需要倒推。只需用硬幣數量除以海盜數量(不包括你自己)。然後把一半的海盜(向下取整)的平均值加上一枚硬幣。
我需要協助解決一個名為「永恆二號」的謎題。解開謎題的獎金高達200萬美元,對我來說是一筆鉅款。這裡有一個採訪鏈接,採訪內容包括遊戲開發者克里斯托弗·蒙克頓(他曾擔任瑪格麗特·撒切爾的顧問)。這款遊戲顯然與賭博無關,但儘管如此,或許你可以在你的網頁上增加一兩句話相關內容。
遊戲開發者在上面給出的連結裡吹噓這個謎題無法解決。我開始覺得他其實是對的,而且他自己是唯一一個最終會透過出售這個(荒謬卻引人入勝的)遊戲致富的人。身為數學家,你會如何解決這種類型的謎題呢?
希望你開心!過去一個月左右,我一直對這個拼圖著迷。我很幸運(或許是不幸)在當地的Borders書店找到了這個256塊的拼圖,但我不得不在eBay上從一個澳大利亞人那裡買下那四個線索的拼圖。
我寫了一個程序,可以輕鬆解決這四個線索謎題。它不到一秒鐘就解開了包含 72 個方塊的線索謎題 #4。我採用的是一個簡單的暴力遞歸程序。我在棋盤上規劃了一條路徑,從邊界開始。在每個位置,程式都會循環遍歷所有未使用的方塊,尋找一個合適的方塊。如果找到,就移動到下一個格子;如果沒有找到,就後退一個格子。
我用兩台電腦連續數週解開這道256塊、價值200萬美元的謎題,卻都遠不及格。我傾向於同意創作者在影片中所說的話:即使你把一千萬台世界上最快的電腦連接起來,它們也未必能在宇宙毀滅前找到答案。你可能會認為我會在開始之前聽從他的警告,但面對一個優秀的謎題,我所有關於時間利用的考慮都拋到九霄雲外了。
我有很多捷徑的想法,但即使它們能把我的程式速度提高十億倍,可能也無濟於事。如果有人能解決這個問題,我會非常欽佩。真正讓我感到不安的是,我感覺到數學中存在一些未被發現的分支,可以輕鬆解決這樣的難題。在那之前,我認為我們能做的最好的就是美其名曰的反覆試驗。今天的計算機實在太慢了,組合數量太多,這種方法的成功率不高。

假設兩座城市之間的距離是1000英里。在無風條件下,飛機可以以500英里/小時的速度飛行。那麼,在無風條件下,往返飛行需要更長的時間嗎?或者,在一個方向上有100英里/小時的順風,在另一個方向上有相同的逆風?
在無風的情況下,單程飛行需要2小時,總共需要4小時。順風時,飛機的速度為600英里/小時,飛行時間為1000/600=1.667小時。逆風時,飛機的速度為400英哩/小時,飛行時間為1000/400=2.5小時。因此,在順風的情況下,總飛行時間為4.167小時,比順風時長多了10分鐘。
這恰恰表明,對平均值進行平均是危險的。你不能說,如果一個行程的平均速度是 500 英里/小時,而另一個行程是 600 英里/小時,那麼整個行程的平均速度就是 500 英里/小時,因為 400 英里/小時的路程涵蓋了更長的時間。
如果這不直觀,想像一下500英里/小時的風速。飛機順風飛行需要1小時,但逆風飛行則需要很長時間。
我最近參加了一個抽獎活動,獎品有7033個,據說中獎機率是1/13。我買了5張彩券。我實際中獎機率是多少?另外,大獎有40個。我中大獎的機率是多少?
為了簡單起見,我們忽略這樣一個事實:你買的彩票越多,每張彩票的價值就越低,因為你正在與自己競爭。也就是說,輸掉五張彩券的機率是 (12/13) 5 = 67.02%。所以至少贏得一次獎的機率是 32.98%。在你買彩券之前,彩券桶裡總共有 7033×13=91,429 張彩券。 91,429-40=91,389 張彩券不是大獎。五張彩券中不了大獎的機率是 (91,389/91429) 5 = 99.78%。所以至少贏得一次大獎的機率是 0.22%,也就是 458 分之一。
我有一個難題,已經嘗試解了幾個月,但毫無進展。如果時間允許,希望您能幫我解答一下,因為它讓我徹夜難眠 :-)。總之,在《超越數數-附錄 CAA》的詞彙表中,有三個由數字和字母組成的序列作為「魔法數字」的詞條。其中一個數字甚至出現在了書的封面上,所以我猜它們一定很重要。有什麼看法嗎?
我很少這麼說,但我確實不知道。正如你在另一封郵件中提到的,他們採用的是美國貨幣序號的格式,兩個字母中間加一個十位數字。出於對版權的尊重,我不會在這裡指出這些數字的具體含義。
我很好奇《永恆2》的謎題挑戰結果怎麼樣了。它解決了嗎?你還在繼續努力嗎?
謝謝你的提問。不,自從我在2008年11月17日的「問巫師」專欄裡寫了這篇文章之後,我就沒再碰過這個問題。根據他們的網站,他們會在2009年12月31日設定“審查日期”,如果有必要,還會在2010年設定。在我看來,這個問題永遠解決不了。
更新:Eternity II 網路尺寸似乎不再存在。
我饒有興致地讀著「巫師」部落格上關於阿諾德‧史瓦辛格否決信的報道。我的問題與州長那荒謬卻又意料之中的回應有關。州長聲稱這只是一個「荒誕的巧合」。儘管有壓倒性的間接證據(該法案的發起人和收信人正是一周前辱罵州長的人),你能否估算一下,一封恰好只有七行的信偶然拼出這句話的概率有多大?我認為,考慮到所使用的字母,這比僅僅給每個字母分配1/26的機率還要小得多。 U、Y,尤其是K,似乎不是常用的單字開頭字母。
如果您容易被冒犯,請跳到下一個問題。
為了讓那些沒有讀過那篇部落格的讀者了解一下,請看一下加州州長阿諾德施瓦辛格的這份備忘錄(PDF)中每一行的首字母,從以字母 F 開頭的行開始。
我的同伴網站「Wizard of Vegas」討論過這個問題。為了找到答案,我在維基百科上找到了英語中第一個單字每個字母的頻率。
按首字母排列的詞頻
| 信 | 頻率 |
| 一個 | 11.60% |
| B | 4.70% |
| C | 3.51% |
| D | 2.67% |
| 埃 | 2.00% |
| F | 3.78% |
| 格 | 1.95% |
| 哈 | 7.23% |
| 我 | 6.29% |
| J | 0.63% |
| 鉀 | 0.69% |
| 左 | 2.71% |
| 米 | 4.37% |
| 否 | 2.37% |
| 哦 | 6.26% |
| 磷 | 2.55% |
| 問 | 0.17% |
| R | 1.65% |
| 秒 | 7.76% |
| T | 16.67% |
| ü | 1.49% |
| 五 | 0.62% |
| 西 | 6.66% |
| 十 | 0.01% |
| 是 | 1.62% |
| Z | 0.05% |
要估算阿諾的資訊確實只是巧合的機率,其公式為:Prob(F) × Prob(U) × ... × prob(U) = 0.0378 × 0.0149 × 0.0351 × 0.0069 × 0.0162 × 0.0626 × 0.0626 × 0.149849999099.0099.098499.09099.09099.09099.09099.09099.090909090909090909。這甚至還沒有考慮到兩個單字之間的空格恰好被換行符取代。
我要感謝 Eliot J. 和 Jonathan F. 對此解決方案的貢獻。
在機場的行李輸送帶上,我需要取的行李越多,等待所有行李出來所需的時間就越長。如果我只有一個行李,我可能需要等到大約一半的行李出來。如果我帶了兩個行李,我的等待時間會更長,如果帶了三個,等待的時間就更長了。假設我的行李隨機地混在一起,那麼根據我的行李數量和行李總數,我需要等待多少行李出來才能取回所有行李,這個通用公式是什麼?
我們先定義一些變量,如下:
n = 您的行李數量
b = 行李總數
隨著行李總數的增加,答案將越來越接近 b×n/(n+1)。對於大型飛機來說,這個答案會比較準確。但是,如果你想要更精確的答案,答案是
[b× combin (b,n)-(combin(i,n)中i=n到b-1的和)]/combin(b,n)
例如,如果總共有 10 個行李,其中 4 個是您的,那麼預計等待時間 =
[10×combin(10,4)-combin(4,4)-combin(5,4)-combin(6,4)-combin(7,4)-combin(8,4)-combin(9,4)]/combin(10,4) = 8.8 袋。
解決方案:
從 b 個袋子中取出 n 個袋子的方法數為 combin(b,n)。因此,所有袋子都出現在前 x 個袋子中的機率為 combin(x,n)/combin(b,n)。最後一個袋子是第 x個袋子的機率為 (combin(x,n)-combin(x-1,n))/combin(b,n),其中 x>=n+1。 x=n 時,機率為 1/combin(b,n)。
因此,預期等待時間與總等待時間的比率為:
n×組合(n,n)/組合(b,n) +
(n+1)×(組合(n+1,n)-組合(n,n))/組合(b,n) +
(n+2)×(組合(n+2,n)-組合(n+1,n))/組合(b,n) +
。
。
。
+
(b-1)×(組合(b-1,n)-組合(b-2,n))/組合(b,n) +
b×(combin(b,n)-combin(b-1,n))/combin(b,n)
取伸縮總和,可以簡化為:
[b×combin(b,n)-combin(b-1,n)-combin(b-2,n)-...-combin(n,n)]/combin(b,n)
後來有一位讀者來信說,答案可以簡化為 n×(b+1)/(n+1)。這可以用歸納法來證明,雖然方法合法,但總讓我感到不滿足。
這個問題是在我的同伴網站Wizard of Vegas的論壇中提出並討論的。
我賣雕塑。平均每賣出七件雕塑,就有一件是烏龜,其餘都是其他類型的雕塑。如果我想在接下來的100件雕塑銷售中,有90%的幾率不缺貨,我需要庫存多少件烏龜?

令 t 為製造的烏龜數量,x 為售出的數量。
pr(x<=t)=0.9
pr(x-14.29<=t-14.29)=0.9
pr((x-14.29)/3.5)<=(t-14.29)/3.5))=0.9
不等式左邊服從標準常態分配(平均數為0,標準差為1)。下一步需要學習統計學入門課程,或具備一定的信念才能接受。
(t-14.29)/3.5 = normsinv(0.9) 這是 Excel 函數。
(t-14.29)/3.5 = 1.282
t-14.29 = 4.4870
t = 18.77
沒人會買0.77個烏龜雕像,所以我會湊整到19個。根據二項分佈,賣出18個或更少烏龜雕像的機率是88.35%,賣出19個或更少烏龜雕像的機率是92.74%。這個問題是在我的同伴網站「維加斯巫師」的論壇上提出並討論的。
五名水手在海難中倖存下來。他們做的第一件事就是收集椰子,並把它們堆成一個大堆。他們原本打算事後平分,但辛苦採摘椰子之後,他們實在太累了。於是他們晚上睡覺,打算明天早上再分椰子。
然而,水手們彼此並不信任。午夜時分,其中一人醒來,想要拿走屬於自己的那一份。他把椰子堆分成五等份,只剩下一個。他把自己的那份埋了起來,把其他四堆椰子合併成一個新的公共椰子堆,然後把剩下的椰子給了一隻猴子。
凌晨 1 點、2 點、3 點和 4 點,其他四名水手也做著同樣的事情。
第二天早上,沒人承認自己做了什麼,他們按照原計畫平分椰子。他們又剩下一個椰子,給了猴子。
原始堆中椰子的最小可能數量是多少?
「向下捲動 100 行即可找到答案。
1
2
3
4
5
6
7
8
9
10
11
12
十三
14
15
16
17
18
19
20
21
22
23
24
二十五
二十六
二十七
二十八
二十九
三十
31
三十二
33
三十四
三十五
三十六
三十七
三十八
三十九
40
41
四十二
43
四十四
45
46
四十七
四十八
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
原先那堆椰子一共有15621個。再向下捲動100行,查看我的答案。
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
設 c 為原堆中椰子的數量,f 為最後一次分配後每位水手的最終份額。
水手 1 拿走他的那一份並將他的椰子給猴子後,將剩下 (4/5)×(c-1) = (4c-1)/5。
水手 2 拿走他的那一份並將他的椰子給猴子後,將剩下 (4/5)×(((4c-1)/5)-1) = (16c-36)/25。
水手 3 拿走他的那一份並將他的椰子給猴子後,將剩下 (4/5)×(((16c-36)/25)-1) = (64c-244)/125。
當水手 4 拿走他的那一份並將他的椰子給猴子後,將剩下 (4/5)×(((64c-244)/125)-1) = (256c-1476)/625。
當水手 5 拿走他的那份並將他的椰子給猴子後,將剩下 (4/5)×(((256c-1476)/625)-1) = (1024c-8404)/3125 個。
第二天早上,每位水手所佔的剩餘份額為 f = (1/5)×(((1024c-8404)/3125)-1) = (1024c-11529)/15625。
那麼,問題是,c 的最小值是多少,使得 f=(1024×c-11529)/15625 為整數。讓我們用 f 來表示 c。
(1024×c-11529)/15625 = f
1024c - 11529 = 15625×f
1024c = 15625f+11529
c = (15625f+11529)/1024
c = 11 + ((15625×f+265)/1024)
c = 11+15×f+(265×(f+1))/1024
那麼,使得 265×(f+1)/1024 為整數的最小 f 是多少? 265 和 1024 沒有共同的因數,所以 f+1 本身必須能被 1024 整除。 f+1 的最小可能值為 1024,因此 f=1023。
因此,c = (15625×1023+11529)/1024 = 15,621。
以下是每個人和猴子收到的椰子數量:
椰子問題
| 水手 | 椰子 |
| 1 | 4147 |
| 2 | 3522 |
| 3 | 3022 |
| 4 | 2622 |
| 5 | 2302 |
| 猴 | 6 |
| 全部的 | 15621 |
向我提出這個問題的戴維‧菲爾默(David Filmer)其實已經知道答案了。實際上,他問的是s名水手的一般情況的公式,但我對5名水手的具體情況已經夠頭疼的了。戴維指出,一般情況下的答案是c = s s+1 - s + 1。
我將把這個證明留給讀者。
以下是該問題替代解決方案的一些連結:
一個人收到兩個裝滿錢的信封。其中一個信封裡的錢是另一個信封的兩倍。這個人選好信封,打開並清點金額後,可以選擇用另一個信封換一個。問題是,換信封對這個人有什麼好處嗎?
由此看來,如果最初的信封金額較小,那麼透過調換,該男子有50%的機率使錢翻倍;如果最初的信封金額較大,那麼有50%的機率使錢減半。因此,設x為最初的信封金額,y為調換後的金額:
y = 0.5×(x/2) + 0.5×(2x) = 1.25x
假設第一個信封裡有 100 美元。那麼,另一個信封裡有 2 × 100 美元 = 200 美元的機率是 50%,另一個信封裡有 (1/2) × 100 美元 = 50 美元的機率也是 50%。在這種情況下,信封的價值為:
0.5×(100美元/2) + 0.5×(2×100美元) = 125美元
這意味著,這位男士光是交換信封,平均就能增加25%的財富!這怎麼可能?
這看似一個數學悖論,但其實只是對期望值公式的濫用。正如你在問題中提到的,另一個信封裡的錢似乎應該比你選擇的那個多25%。然而,如果你買了那個信封,那麼你一開始就應該選擇另一個信封。此外,如果你在決定換信封之前沒有打開信封,你就可以永遠用這個論點來回切換。顯然,期望值論證中一定存在一些缺陷。問題是,缺陷在哪裡?
這些年來,我花了很多時間閱讀和討論這個問題。我聽過和讀過很多關於為什麼 y=.5x + .5*2x = 1.25x 的論證是錯誤的解釋。很多人用了好幾頁的高等數學來解釋,但我認為沒有必要。這是一個簡單的問題,需要一個簡單的答案。所以,這是我的嘗試。
你必須非常謹慎地處理這樣一個事實:一個信封裡的錢是另一個信封裡的兩倍。我們把小信封裡的錢記為S,大信封裡的錢記為L。這樣:
長=2×小
S=0.5×L
請注意 2 和 0.5 因子是如何應用於不同信封的。您不能同時採用這兩個因子並將它們應用於相同的金額。如果第一個信封中有 100 美元,那麼如果是較小的信封,另一個信封中就有 200 美元。如果 100 美元是較大的信封,那麼另一個信封中就有 50 美元。因此,另一個信封中有 50 美元或 200 美元。但是,您不能由此跳到說每個信封中有 50% 的機率。這是因為那樣就等於將 0.5 和 2 因子應用於相同的金額,而您無法做到這一點。如果一開始就不知道獎金分配情況,您就無法將可能的金額分配給第二個信封。
如果 0.5x/2x 的論點是錯誤的,那麼如何正確設定另一個信封的預期值呢?我會這樣說:兩個信封之間的差額為 LS = 2S-S = S。交換信封,你要么獲得 S,要么損失 S,無論它是多少。如果兩個信封分別有 50 美元和 100 美元,那麼交換信封將獲得或損失 50 美元。如果兩個信封分別有 100 美元和 200 美元,那麼交換信封將獲得或損失 100 美元。無論哪種方式,交換信封的預期收益都是 0。我想我可以說,如果第一個信封有 100 美元,那麼另一個信封的差額有 50% 的可能性是 50 美元,有 50% 的可能性是 100 美元。所以預期差額是 75 美元。因此,另一個信封的預期價值為 0.5×($100+$75) + 0.5×($100-$75) = 0.5×($175+$25) = $100。
希望以上內容對您有幫助。這個問題總是會引發很多評論。如果您有意見,請不要直接寫信給我,而是在我的“維加斯巫師”論壇上發布。連結如下。
這個問題是在我的同伴網站Wizard of Vegas的論壇中提出並討論的。
連結
假設有一場三人決鬥,參與者有A、B和C。他們為了爭奪一個女人而決鬥至死。他們都是紳士,並且都同意以下規則。
- 三位參與者形成一個三角形。
- 每顆子彈只有一顆。
- A 先走,然後 B,最後是 C。
- A 擊中預定目標的機率是 10%。
- B 擊中預定目標的機率為 60%。
- C 擊中預定目標的機率為 90%。
- 沒有發生意外槍擊事件。
- 允許向空中射擊(故意射偏)和射擊自己,並且總是成功的。
- 如果任何一輪結束後仍有兩到三名倖存者,則每人獲得一顆新子彈。之後,他們將按照相同的順序輪流射擊,跳過任何已經死亡的玩家。
- 三位參與者都是完美的邏輯學家。
A 最初應該瞄準誰?他針對每個初始目標的生存機率是多少?
BBC 節目《相當有趣》討論了這個謎題。向下捲動 100 行即可查看答案和解答。
1
2
3
4
5
6
7
8
9
10
11
12
十三
14
15
16
17
18
19
20
21
22
23
24
二十五
二十六
二十七
二十八
二十九
三十
31
三十二
33
三十四
三十五
三十六
三十七
三十八
三十九
40
41
四十二
43
四十四
45
46
四十七
四十八
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
以下是我根據每個初始目標計算出的 A 獲勝的機率。如你所見,故意向空中射擊可以最大化 A 的獲勝機率。
真實賠率
| 策略 | 機率獲勝 |
| 空氣 | 13.887% |
| 一個 | 0.000% |
| B | 12.560% |
| C | 13.094% |
為了解答這個問題,我們用 Pr(X) 表示一輪之後 X 組(且僅剩 X 組)存活的機率。以 Pr(X*) 表示 X 組最終贏得該輪的機率,重複此過程直至遊戲狀態因有人被擊中而改變。以 Pr(X**) 表示玩家 X 是唯一倖存者的機率。為了找到最終的機率,我們先來看看兩人的狀態。顯然,雙方都會向對方射擊。
A 與 B
- Pr(A) = 0.1
- Pr(B) = 0.9×0.6 = 0.54
- Pr(AB) = 0.9×0.4 = 0.36
如果兩人都倖存下來,那麼他們將重複這個過程,直到只剩下一個倖存者。因此,最終倖存者的機率為:
- Pr(A*) = Pr(A)/(1-Pr(AB)) = 0.1/0.64 = 0.15625
- Pr(B*) = Pr(B)/(1-Pr(AB)) = 0.54/0.64 = 0.84375
A 與 C
- Pr(A) = 0.1
- Pr(C) = 0.9×0.9 = 0.81
- Pr(AC) = 0.9×0.1 = 0.09
如果兩人都倖存下來,那麼他們將重複這個過程,直到只剩下一個倖存者。因此,最終倖存者的機率為:
- Pr(A*) = Pr(A)/(1-Pr(AC)) = 0.1/0.91 = 0.10989011
- Pr(C*) = Pr(B)/(1-Pr(AC)) = 0.81/0.91= 0.89010989
B 與 C
- Pr(B) = 0.6
- Pr(C) = 0.4×0.9 = 0.36
- Pr(BC) = 0.$×0.1 = 0.04
如果兩人都倖存下來,那麼他們將重複這個過程,直到只剩下一個倖存者。因此,最終倖存者的機率為:
- Pr(B*) = Pr(A)/(1-Pr(BC)) = 0.6/.96 = 0.625
- Pr(C*) = Pr(B)/(1-Pr(BC)) = 0.36/.96= 0.375
現在我們來分析三人的狀況。我們先來考慮一下 A 瞄準 B 的情況。
三人遊戲-A 瞄準 B
如果A擊中B,那麼C肯定能存活,但可能擊中A,也可能擊不中。因此,擊中B的兩種可能結果是AC和C。如果A擊中B未擊中,那麼B會瞄準威脅更大的C。如果B擊中C,那麼A和B都能存活。如果B擊中C未擊中,那麼C會瞄準威脅更大的B。如果C擊中B未擊中,那麼A和C都能存活。如果C擊中B,那麼A和C都能存活。因此,可能的結果是C、AB、AC和ABC。
- Pr(A) = 0。
- Pr(B) = 0。
- Pr(C) = 0.1 × 0.9 = 0.09。這是透過 A 擊中 B,然後 C 擊中 A 來實現的。
- Pr(AB) = 0.9 × 0.6 = 0.54。這是透過 A 擊中 B,然後 B 擊中 C 來實現的。
- Pr(AC) = 0.1 × 0.1 + 0.9 × 0.4 × 0.9 = 0.334。這可以透過兩種方式實現。第一種是 A 命中 B,然後 C 未命中 A。第二種是 A 未命中 B,B 未命中 C,然後 C 命中 B。
- Pr(BC) = 0。
- Pr(ABC) = 0.9 × 0.4 × 0.1 = 0.036。這是透過三項全部缺失實現的。
按照與雙人情況相同的邏輯,我們可以將每個結果除以 (1-Pr(ABC))=0.964 來找到每個狀態的機率,假設遊戲狀態在回合之後確實發生了變化。
- Pr(C*) = 0.09/0.964 = 0.093361。
- Pr(AB*) = 0.54/0.964 = 0.560166。
- Pr(AC*) = 0.334/0.964 = 0.346473。
從雙人對決的情況來看,如果是A和B,那麼A獲勝的機率為0.15625,B獲勝的機率為0.84375。如果是A和C,那麼A獲勝的機率為0.109890,C獲勝的機率為0.890110。
- Pr(A**) = (0.560165975 × 0.15625) + (0.346473029 × 0.10989011) = 0.125600。 A 可以透過兩種方式獲勝:(1) 進入 AB 狀態,然後獲勝;(2) 進入 AC 狀態,然後獲勝。
- Pr(B**) = 0.560166 × 0.84375 = 0.472640。若B進入AB狀態,則B獲勝,B為勝者。
- Pr(C**) = 0.093361 + (0.346473 × 0.890110) = 0.401760。 C 可以透過 A 殺死 B,然後 C 在第一輪殺死 A 來獲勝,或透過進入狀態 AC,然後 C 獲勝。
因此,如果 A 的策略是先瞄準 B,那麼他成為唯一倖存者的機率是 12.56%。
三人遊戲-A 瞄準 C
如果A擊中C,那麼B肯定會倖存,但可能會擊中A,也可能不會。因此,擊中C的兩種可能結果是AB和B。如果A沒有擊中C,那麼B會瞄準威脅更大的C。如果B擊中C,那麼A和B都會存活。如果B沒有擊中C,那麼C會瞄準威脅更大的B。如果C沒有擊中B,那麼A和B都會存活。如果C擊中B,那麼A和C都會存活。因此,可能的結果是B、AB、AC和ABC。
- Pr(A) = 0。
- Pr(B) = 0.1 × 0.6 = 0.06。
- Pr(C) = 0。
- Pr(AB) = (0.1 × 0.4) + (0.9 × 0.6) = 0.04+0.54 = 0.58。這可以透過兩種方式實現。第一個是 A 擊中 C,然後 B 擊中 A。第二個是 A 擊中 B,然後 B 擊中 C。
- Pr(AC) = 0.9 × 0.4 × 0.9 = 0.324。這是透過 A 缺失 C、B 缺失 C 以及 C 命中 B 來實現的。
- Pr(BC) = 0。
- Pr(ABC) = 0.9 × 0.4 × 0.1 = 0.036。這是透過三項全部缺失實現的。
按照與雙人情況相同的邏輯,我們可以將每個結果除以 (1-Pr(ABC))=0.964 來找到每個狀態的機率,假設遊戲狀態在回合之後確實發生了變化。
- Pr(B*) = 0.06/0.964 = 0.062241。
- Pr(AB*) = 0.58/0.964 = 0.601660。
- Pr(AC*) = 0.324/0.964 = 0.336100。
按照與 A 針對 B 的情況的解決方案相同的邏輯:
- Pr(A**) = (0.601660 × 0.15625) + (0.336100 × 0.10989011) = 0.130943。
- Pr(B**) = 0.062241 + 0.601660 × 0.84375 = 0.569891。
- Pr(C**) = 0.336100 × 0.890110 = 0.299166。
因此,如果 A 的策略是先瞄準 C,那麼他成為唯一倖存者的機率是 13.09%。
三人 — A 故意失手
A故意射偏後,B會瞄準威脅更大的C。如果B擊中C,A和B都會存活。如果B射偏C,C會瞄準威脅更大的B。如果C射偏B,A和B都會存活。如果C射偏B,A和C都會存活。因此,可能的結果是AB、AC和ABC。
- Pr(A) = 0。
- Pr(B) = 0。
- Pr(C) = 0。
- Pr(AB) = 0.6。這是透過 B 擊中 C 來實現的。
- Pr(AC) = 0.4 × 0.9 = 0.36。這是透過 B 未命中 C,然後 C 命中 B 來實現的。
- Pr(BC) = 0。
- Pr(ABC) = 0.4 × 0.1 = 0.04。這是透過全部三個缺失來實現的。
按照與雙人情況相同的邏輯,我們可以將每個結果除以 (1-Pr(ABC))=0.96 來找到每個狀態的機率,假設遊戲狀態在回合之後確實發生了變化。
- Pr(AB*) = 0.6/0.96 = 0.625。
- Pr(AC*) = 0.36/0.96 = 0.375。
按照與 A 針對 B 的情況的解決方案相同的邏輯:
- Pr(A**) = (0.625 × 0.15625) + (0.375 × 0.109890) = 0.138865。
- Pr(B**) = 0.625 × 0.84375 = 0.527344。
- Pr(C**) = 0.375 × 0.890110 = 0.333791。
因此,如果 A 的策略是先瞄準 C,那麼他成為唯一倖存者的機率是 13.89%。
這個問題是在我的同伴網站Wizard of Vegas的論壇中提出並討論的。
一次比較兩個元素,對清單進行排序的最快方法是什麼,從而最大限度地減少比較次數?
有幾種方法效果差不多。不過,我發現最容易理解的方法是合併排序。它的工作原理如下:
- 將列表一分為二。繼續將每個子集再分成兩部分,直到每個子集的大小都為 1 或 2。
- 對 2 的每個子集進行排序,將較小的成員放在最前面。
- 將子集對合併在一起。不斷重複,直到只剩下一個排序好的清單。
合併兩個清單的方法是比較每個清單的第一個成員,並將較小的放入一個新清單中。然後重複此操作,將較小的一個放在上一次比較的較小成員之後。不斷重複此操作,直到兩組合併為一個有序組。如果原始清單之一為空,則可以將另一個清單附加到合併後清單的末尾。
下表顯示了根據清單中元素的數量所需的最大比較次數。
合併排序
| 元素 | 最大比較數 |
| 1 | 0 |
| 2 | 1 |
| 4 | 5 |
| 8 | 17 |
| 16 | 49 |
| 三十二 | 129 |
| 64 | 321 |
| 128 | 769 |
| 256 | 1,793 |
| 512 | 4,097 |
| 1,024 | 9,217 |
| 2,048 | 20,481 |
| 4,096 | 45,057 |
| 8,192 | 98,305 |
| 16,384 | 212,993 |
| 32,768 | 458,753 |
| 65,536 | 983,041 |
| 131,072 | 2,097,153 |
| 262,144 | 4,456,449 |
| 524,288 | 9,437,185 |
| 1,048,576 | 19,922,945 |
| 2,097,152 | 41,943,041 |
這個問題是在我的同伴網站Wizard of Vegas的論壇中提出並討論的。
2010年10月29日, 《拉斯維加斯評論報》刊登了一項關於里德和安格爾參議員競選的民意調查。調查顯示,在625名潛在選民的調查中,安格爾的得票率為49%,里德的得票率為45%。調查也顯示,誤差幅度為4%。以下是我的問題:
- Angle 獲勝的機率是多少?
- Angle 的得票率的 95% 信賴區間是多少?
- 誤差幅度是什麼意思?
抱歉,回覆得有點過時。以下是我在選舉前寫的。
首先,我要剔除剩下的6%,他們要么猶豫不決,要么會把選票浪費在第三方候選人身上,或者「以上皆非」(在內華達州,這兩者是可以考慮的)。有些人可能不同意這個假設。說實話,忽略他們的另一個原因是,如果候選人超過兩位,計算起來會更加複雜。所以,四捨五入後,安格爾有306票,里德有281票,樣本總數為587票。
我將使用標準常態近似來回答這個問題。如果我是一個完美主義者,那麼我會使用T分佈,因為實際的平均值和變異數是未知的。然而,在我看來,對於常態分佈來說,587的樣本量是完全可以接受的。
樣本數 = 306+281 = 587。
角度樣本平均值為 306/587 = 0.521295。
平均值的估計標準差為 (0.521295 × 0.478705 / (587-1))^0.5 = 0.0206361。
Angle 的 50% 以上的份額為 (0.521295-0.5)/0.0206361 = 1.031917 個標準差。
根據常態分佈,Reid 最終結果超出預期 1.031917 個標準差的機率為 0.151055。這可以在 Excel 中使用函數 NORMSDIST(-1.031917) 計算得出。因此,Angle 獲勝的機率為 1-0.151268 = 84.89%。
若要建立 95% 的置信區間,請注意高斯曲線兩側 2.5% 的點與平均值之間的標準差為 1.959964。這可以在 Excel 中使用函數 NORMSINV(0.975) 計算。如前所述,樣本平均值的估計標準差為 0.0206361。因此,兩位候選人的得票率與民調結果之間的標準差在 0.0206361×1.959964 = 0.040446 以內的可能性為 95%。因此,Angle 的 95% 信賴區間為 0.521295 +/- 0.040446 = 48.08% 至 56.17%。
有人告訴我,如果這樣表述在數學上是不正確的:「Angle在所有Angle/Reid選票中的份額有95%的可能性落在48.08%到56.17%之間。」我最初的回答就是這樣的,但兩位統計學家對我的措辭感到震驚。解釋一下他們的回答,他們說我必須使用被動語態,說「48.08%和56.17%將以95%的機率圍繞Angle的份額」。 說實話,在我看來,這聽起來是一樣的。然而,他們強調置信區間是隨機的,而Angle的份額是不可改變的,而我最初的措辭暗示了相反的意思。無論如何,我希望頻率統計專家們會對第二種表述感到滿意。
「誤差幅度」是95%信賴區間兩端差值的一半。在本例中,(56.17% - 48.08%)/2 = 4.04%。
作為後續,以下是實際結果:
里德:361,655
角度:320,996
其他:21,979
因此,不計入「其他」選票,里德獲得了53.0%的選票,安格爾獲得了47.0%的選票。里德輕鬆贏了6%。這不禁讓人思考,民調結果為何如此懸殊。是偶然嗎?選民改變了主意嗎?還是民調結果本身就很糟糕?我把這些問題留給讀者去思考(我討厭教科書上這麼說)。
這個問題是在我的同伴網站Wizard of Vegas的論壇中提出並討論的。
我試用了你們的精算計算器。為什麼我達到預期死亡年齡的機率不到 50%?
你混淆了平均值和中位數。我們以我的情況為例。我是45歲的男性。我的預期壽命是78.11歲,但我活到80歲的機率是50.04%。
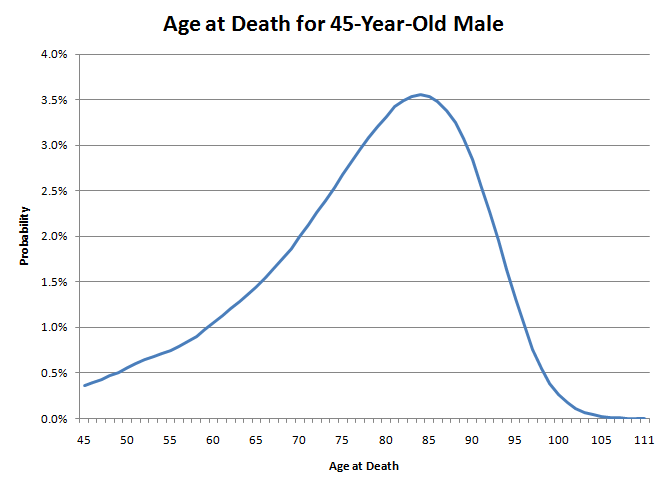
我的死亡年齡就像向這張圖投擲飛鏢一樣。注意左尾比右尾粗得多。這意味著我現在死亡的機率很低。然而,隨著年齡的增長,明年死亡的機率會越來越高。例如,對於一個45歲的男性來說,活到46歲的機率相當高,達到99.64%。然而,到了85歲,活到86歲的機率只有89.21%。這就像大自然慢慢地在你的背後捅刀子。起初它可能不會殺死你,但隨著時間的流逝,它殺死你的機率會慢慢增加。然而,一旦你到了七十多歲後期,大自然就會對你不再玩命,開始真正捅刀子。
因此,如果許多45歲的男性向這張圖投擲飛鏢,49.96%的人將在45歲至79歲之間命中,50.04%的人將在80歲至111歲之間命中。然而,幸運地落在圖表右側的那一半人可能活不過80歲。男性一旦達到80歲,預期壽命也只有7.78年。同時,那些不幸活不到80歲的人,許多人的壽命會比80歲短得多。因此,正是大量年輕人的死亡拉低了平均壽命。
對於類似的情況,考慮一個數字為 10、20、30、31、32、33 的骰子。平均值為 26,但擲出大於該值的機率為 2/3。
舉個例子來說明平均值和中位數的不同之處,假設我們在樣本中再增加兩個死亡病例。一個在46歲時死亡,另一個在81歲時死亡。活到80歲的機率保持不變,但45歲時的平均壽命會下降。
這個問題是在我的同伴網站Wizard of Vegas的論壇中提出並討論的。
想像一條無限彈性的橡皮筋,未拉伸時長1公里,以每秒1公里的速度膨脹。接下來,想像橡皮筋的一端有一隻螞蟻。當橡皮筋開始膨脹時,螞蟻以相對於目前位置每秒1公分的速度向另一端爬行。螞蟻最終會到達另一端嗎?如果會,什麼時候?
是的, 100,000 -1秒後就會了。請參閱我的mathproblems.info網站,問題 206,其中有兩個答案。
這個問題是在我的同伴網站Wizard of Vegas的論壇中提出並討論的。
你認為更高的燃油效率值得你額外花點錢買一輛混合動力車嗎?你需要開多少英里才能收支平衡?
問得好。為了回答這個問題,我考慮了一輛豐田漢蘭達,我正在考慮購買。標準混合動力車型的零售價為37,490美元。同一款四輪驅動車型,非混合動力車型的零售價為29,995美元。所以,混合動力車型的成本增加了7,495美元。
混合動力車型的油耗為28英里/小時(市區和高速公路)。非混合動力車型的油耗分別為17英里/小時(市區)和22英里/小時(高速公路)。我們取平均值19.5英里/小時。
損益平衡哩程數的一般公式為 h×m h ×m r /(g×(m h -m r )),其中
h = 混合的額外成本。
g = 一加侖汽油的成本。
m r = 非混合動力車的里程數(「r」代表普通汽車)。
m h = 混合動力車的里程數。
下表使用此公式來找到每加侖 2 美元至 5 美元的各種汽油價格的損益平衡點。
混合損益平衡點
| 天然氣成本 | 英里數 |
| 2.00 美元 | 240,722 |
| 2.25 美元 | 213,975 |
| 2.50 美元 | 192,577 |
| 2.75 美元 | 175,070 |
| 3.00 美元 | 160,481 |
| 3.25 美元 | 148,136 |
| 3.50 美元 | 137,555 |
| 3.75 美元 | 128,385 |
| 4.00 美元 | 120,361 | 4.25 美元 | 113,281 |
| 4.50 美元 | 106,987 |
| 4.75 美元 | 101,357 |
| 5.00 美元 | 96,289 |
因此,以拉斯維加斯目前每加侖3美元的油價計算,您需要行駛超過160,481英里才能獲得更高的燃油經濟性。這還不包括混合動力汽車可能帶來的其他費用,例如昂貴的電池更換成本,以及任何因減少化石燃料消耗而產生的環保積分。
這個問題是在我的同伴網站Wizard of Vegas的論壇中提出並討論的。
除了同卵雙胞胎之外,我與同胞兄弟姊妹的基因有多少比例是相同的?
1/2。
如果我們用基諾彩券來類比,每個人都有40個基因,每個基因都代表一個基諾球。然而,每個球都有一個唯一的編號。當兩個沒有血緣關係的人交配時,就像把他們兩人的80個球組合成一個漏斗,然後隨機選擇40個基因作為交配後代的基因。
所以,當你受孕時,你得到了一半的彩球,另一半則被浪費了。當你的兄弟姊妹受孕時,他/她得到了你出生時抽取的彩球的一半,以及另一半未被抽取的彩球。所以,你們的基因有50%是相同的。這和基諾彩券如果抽出40個號碼,連續兩次抽出平均會有20個相同的彩球的原因是一樣的。
這個問題是在我的同伴網站Wizard of Vegas的論壇中提出並討論的。
一家生產桌椅的工廠配備了10台鋸、6台車床和18台砂光機。製作一張椅子需要鋸子10分鐘、車床5分鐘和砂光5分鐘才能完成。製作一張桌子需要鋸5分鐘、車床5分鐘和砂光20分鐘才能完成。一張椅子售價10美元,一張桌子售價20美元。工廠每小時應生產多少張桌椅以獲得最高收益?收益是多少?
設c代表每小時製作的椅子數量,t代表桌子數量。每小時收入為10×c + 20×t。
10把鋸子每小時鋸600分鐘。已知一張椅子鋸10分鐘,一張桌子鋸5分鐘。因此,每小時產量限制為:
(1)10c + 5t <= 600
6台車床每小時加工時間共360分鐘。我們已知,鋸一把椅子需要5分鐘,鋸一張桌子需要5分鐘。因此,每小時產量限制為:
(2)5c + 5t <= 360
18台砂光機每小時可進行1080分鐘的砂光作業。我們假設一張椅子需要鋸子5分鐘,一張桌子需要鋸子20分鐘。因此,每小時的產量限制為:
(3)5c + 20t <= 1080
下圖顯示了三組機器所施加的三個約束。工廠可以生產符合所有三條線的任意椅子和桌子組合。問題是,在三條線下,哪個組合能帶來最大的效益。
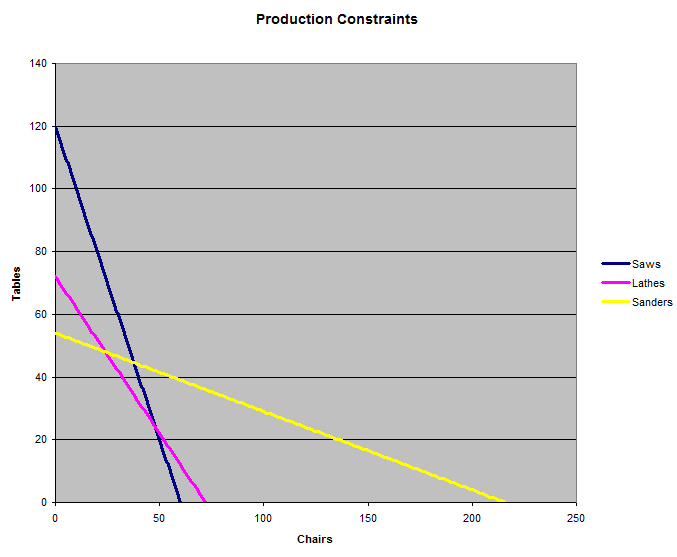
照理說,答案應該是兩條線的交點、所有椅子或所有桌子。那麼,讓我們找出這兩條線的交點。首先,讓我們找出公式 (1) 和公式 (2) 的交點。我們可以將 <= 表達式改為 =,以最大限度地發揮機器的潛力。
(1)10美分+5噸=600
(2)5c + 5t = 360
由 (1) 減去 (2):
5美分=240
c = 48
將 48 代入公式 (1) 中,得到 c:
10×48 + 5t = 600
5t = 120
t = 24
因此,方程式 (1) 和 (2) 在 48 把椅子和 24 張桌子處相交。
接下來,讓我們找出方程式 (2) 和 (3) 的交點:
(2)5c + 5t = 360
(3)5c + 20t = 1080
從 (3) 減去 (2):
15噸=720
t = 48
將其代入 (2) 或 (3) 中,我們可以解出 c,即 24。
因此,方程式 (2) 和 (3) 在 24 張椅子和 48 張桌子處相交。
我們不需要費心去尋找方程式 (1) 和 (3) 的交點,因為我們可以從圖中看到鋸線和砂光機線的交點在車床約束之外。
也可能只做椅子才是正確答案。圖表顯示,鋸子是只做椅子的最大限制因素。根據公式 (1),如果我們將桌子數量代入 0,則 c=60。
另一種可能性是只做桌子。圖表顯示,砂磨機將是最大的限制因素。將0張椅子代入公式(3),我們發現最多只能做54張桌子。
下圖顯示了每個可行答案的總收入。記住,每張椅子的收入是10美元,每張桌子的收入是20美元。
每小時總收入
| 椅子 | 表格 | 收入 |
| 0 | 54 | 1,080美元 |
| 24 | 四十八 | 1,200美元 |
| 四十八 | 24 | 960美元 |
| 60 | 0 | 600美元 |
國王有一桶滿滿的酒。
星期一晚上,一個僕人從桶子裡偷走了三個杯子,並用三杯水代替。
週二晚上,另一個僕人從已經稀釋的酒桶中偷走了三杯酒,並用三杯水代替。
星期三晚上,又有一個僕人從已經稀釋的酒桶裡偷走了三杯酒,並用三杯水代替。
週四早上,酒桶 50% 是酒,50% 是水。
桶子裡最初有多少酒?
這是答案和解決方案(PDF)。
有關此問題的討論,請訪問我在Wizard of Vegas 的論壇。
如果我有一碗200顆彩虹糖,其中3顆就能殺死我,那麼如果我抓起12顆彩虹糖並全部吃掉,我死亡的機率是多少?假設只需要一顆有毒的彩虹糖就能殺死我。
答案是 1-combin(197,12)/combin(200,12) = 17.02%。
有關此問題的更多討論,請訪問我在Wizard of Vegas 的論壇。
一個外星人綁架了十位邏輯學家,並把他們關在一個房間裡。他向他們解釋說,他首先把他們排成一排,從高到矮,每個人都面向前面第二矮的人,這樣每個人都能看到所有矮個子的邏輯學家,但看不到更高的邏輯學家。然後他解釋說,他會給每個人戴上一頂黑色或白色的帽子,但沒有人能看到自己帽子的顏色,只能看到矮個子邏輯學家的帽子。黑白帽子的分佈可以是任意的,不一定是五頂五頂。
外星人隨後解釋說,他會從最高的開始,依序詢問每位邏輯學家帽子的顏色。邏輯學家可以聽到前面人的回答。除了黑白答案外,遊戲開始後,他們不得以任何方式溝通。如果超過一位邏輯學家答錯,他們就會被全部吃掉。如果至少有九個答案正確,他們將被安全送回地球。然後,外星人會給他們一些時間制定策略。他們的策略應該是什麼?
以下是一種可行的策略。讓第一個行動的邏輯學家,如果看到其他九位邏輯學家戴的帽子數量為偶數,就說“黑色”,如果看到其他九位邏輯學家戴的帽子數量為奇數,就說“白色”。他有50%的機率匹配自己帽子的顏色,所以他是唯一一個可以犯錯的人。無論他說了什麼,都將其定義為“運行顏色”。
接下來,第二位行動的邏輯學家將計算較矮的八位邏輯學家的黑帽數量,並用與第一位邏輯學家相同的奇偶方法將其與顏色匹配。如果結果與第一位邏輯學家給出的顏色一致,那麼他一定戴著白帽,並應選擇白色。如果結果不一致,那麼他一定戴著黑帽,並應選擇黑色。如果他說“白色”,則當前顏色保持不變。如果他說“黑色”,則當前顏色將翻轉為相反的顏色。
接下來,第三位邏輯學家的操作與第二位完全相同,但會數一下其他七位較矮的邏輯學家手中的黑帽數量。同樣,如果他同意當前顏色,他會說“白色”,當前顏色保持不變。如果他不同意當前顏色,他會說“黑色”,當前顏色將翻轉。
其他邏輯學家也會做同樣的事情。
當然,他們也可以輕易地將黑色與奇數連結起來,將白色與偶數連結起來。重要的是,他們都同意哪種顏色代表哪種奇偶校驗。無論採取哪一種策略,都會導致第二到第十位邏輯學家認為所有答案都正確,而第一位邏輯學家則有50%的機率活下來。這個策略適用於任何數量的邏輯學家。
阿克塞爾和鮑伯各自有一副52張的牌。兩人都隨機洗牌。然後,他們同時從每副牌中翻出一張牌。他們同時翻出同一張牌至少一次的機率是多少?
答案很容易估算為 1-(51/52) 52 = 0.63568648。然而,估算在智力上實在難以令人滿意。所以,讓我們來求一個精確的解吧!
步驟 1:首先,考慮第二副牌的排序方式數,其中第一張牌是 1。答案是排序其他 51 張牌的方式數,即 51! = 1551118753287382280224243016469303211063259720016986112000000000000。
任何牌都能搭配第一副牌,所以我們必須對所有 52 張牌都進行相同的操作。這樣一來,就有 52*51! = 52! 種組合,其中至少有一張牌匹配。
步驟 2:然而,步驟 1 會重複計算兩張牌相符的所有情況。例如,如果前兩張牌是 1 和 2,那麼我們需要將其他牌的 50! 種排列方式計算兩次,第一次將 1 作為第一張牌,第二次將 2 作為第二張牌。從 52 張牌中選出 2 張牌的方式數為 combin(52,2) = 1326。每兩張牌的組合,其他牌的排列方式有 50! = 30414093201713378043612608166064768844377641568960512000000000000000 種。因此,對於步驟 2,我們需要減去 combin(52,2)*50! = (52*51/2!)*50! = 52!/2! 種組合。
步驟 3:接下來,考慮隨機牌堆中前三張牌的順序為 1、2 和 3 的情況。其餘 49 張牌有 49! 種排序方法。在初步步驟中,我們會數三次,以找出至少一張相符的牌。然後,在第二步驟中,我們會減去所有 combin(3,2)=3 種從這三張牌中選擇 2 張的方法。因此,這種情況會被計算 3-3=0 次,因此我們需要將它們加回去。有 combin(52,3) 種選擇至少 3 張配對牌的情況。因此,我們需要重新加入 combin(52,3)*49! = 52*51*50*49!/3! = 52!/3! 種組合。
步驟 4:接下來,考慮隨機牌堆中前四張牌的順序為 1、2、3 和 4 的情況。其餘 48 張牌有 48! 種排序方法。在初始計數至少一張匹配牌的步驟中,我們需要數四次。然後,在步驟 2 中,我們需要減去所有 combin(4,2)=6 種從這四張牌中選擇兩張的方法。然後,我們需要加上所有 combin(4,3)=4 種從這四張牌中選擇三張的方法。因此,每種情況都有 4-6+4=2 種計數方法。因此,我們需要減去其中一種計數方法,使每種情況都只計算一次。共有 combin(52,4)*48! = 52*51*50*49*48!/4! = 52!/4! 種需要加回去的情況。
我們將繼續這樣做,交替進行加法和減法來修正重複計算。
最後,隨機牌堆中至少有一張牌與有序牌堆匹配的情況數量 = combin(52,1)*51! - combin(52,2)*50! + combin(52,3)*49! - combin(52,4)*48! ... - combin(52,52)!1! = 52,4)*48! ... - combin(52,52)!1 52!/4! ... - 52!/52! = x = 333239808909468890675694068318655265019682314241643033726180828783。
共有 52 種方法可以排列 52 張牌! = y = 5271776154963652194226185415451226599692124538619822080000000000000 種方法可以排列 52 張牌。
因此,答案是 x/y = 0.6321205588285576784044762298
沒有匹配的機率是 1-(x/y) = 0.3678794411714423215955237702。
如果這個數字看起來很熟悉,那就對了。 1/e = 0.3678794411714423215955237702。
因此,答案可以非常接近地估計為 1-(1/e)。
致謝
數學計算是在Pari/GP中進行的
這個問題已在我的Wizard of Vegas論壇中提出並討論。
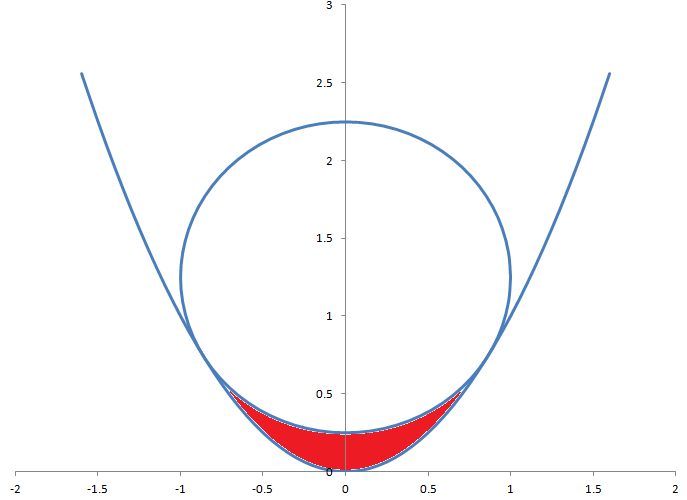
半徑為 1 的圓與方程式 y=x 2的拋物線相切。圓與拋物線之間的紅色區域面積是多少?
點擊下面的按鈕以取得答案。
這是我的解決方案。 (PDF)
我在Wizard of Vegas論壇上提出並討論了這個問題。
我從Mind Your Decisions的 Presh Talwalker 那裡遇到了這個問題。
一位賭場荷官正在研究一種新的三張牌撲克遊戲。她從一副標準牌中取出所有人頭牌,並徹底洗牌。然後,她給玩家1發了3張牌,給玩家2發了3張牌,給玩家3發了3張牌,最後給玩家4發了3張牌。四手牌都包含順子(任意花色的JQK)的機率是多少?

[劇透=解]
第一手牌是AKQ的機率是1*(8/11)*(4/10) = 29.09%。
假設第一手牌已經是 AKQ,那麼第二手牌是 AKQ 的機率等於 1*(6/8)*(3/7) = 32.14%。
假設第一和第二手牌都是 AKQ,那麼第三手牌是 AKQ 的機率等於 1*(4/5)*(2/4) = 40.00%
由於前三手牌都是AKQ,所以剩下的牌一定是AKQ。因此,機率是上述三個機率的乘積,即216/5775 = 約0.037402597。
[/spoiler]我在Wizard of Vegas論壇上提出並討論了這個問題。
隨機內接於半徑為 1 的圓的矩形的平均面積和周長是多少?
好問題。以下是我的答案:
這是我對這兩個問題的解決方案(PDF)。
求一個十位數,滿足:
- 這個數字的第一位數字是整個數字中 0 的個數。
- 這個數字的第二位數字是整個數字中 1 的個數。
- 這個數字的第三位數字是整個數字中 2 的個數。
- 該數字的第 4 位數字是整個數字中 3 的個數。
- 該數字的第 5 位數字是整個數字中 4 的數量。
- 該數字的第 6 位數字是整個數字中 5 的數量。
- 該數字的第 7 位數字是整個數字中 6 的數量。
- 該數字的第 8 位數字是整個數字中 7 的數量。
- 該數字的第 9 位數字是整個數字中 8 的數量。
- 這個數字的第 10 位是整個數字中 9 的個數。
[spoiler=答案]6,210,001,000[/劇透]
我在Wizard of Vegas論壇上提出並討論了這個問題。
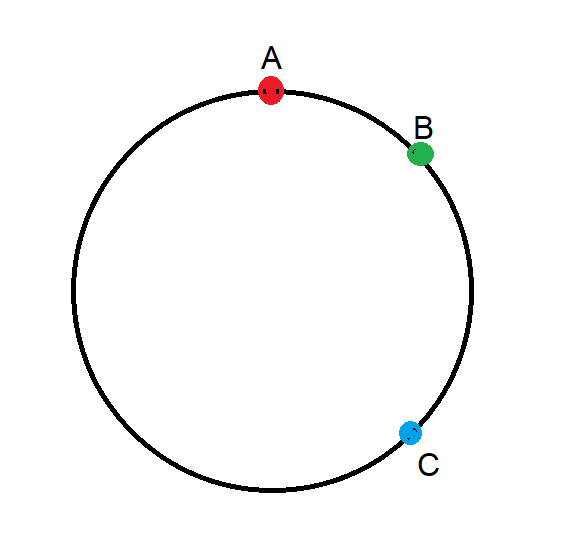
三個點隨機均勻地分佈在半徑為 1 的圓上。沿著圓週測量距離時,這三個點之間的預期最小距離是多少?
愛麗絲和比爾花了 3 個小時粉刷一棟房子。
愛麗絲和辛蒂花了 4 個小時粉刷一棟房子。
比爾和辛蒂花了 5 個小時粉刷一棟房子。
如果全部都畫的話需要多久?
[spoiler=答案]120/47 =~ 2.553191 小時[/劇透]
這是我的解決方案(PDF)。


