概率 - 硬幣
如果將一枚硬幣拋 1000 次,那麼正面總數在 452 到 548 範圍內的機率是多少?
對於這個問題,我們可以使用二項分佈的常態近似。正面朝上的次數的變異數為 1000*(1/2)*(1/2)=250。因此標準差為 250 1/2 =15.8114。正面朝上次數少於 548 次的機率為 normdist((548+0.5-500)/15.8114) = 0.998920,其中 normsdist 是 Excel 函數,用於計算平均值為 0、標準差為 1 的常態分佈隨機變數落入給定 Z 分數機率的機率。接下來,我們減去正面朝上次數少於 452 次的機率。結果為 normdist((452-0.5-500)/15.8114) = 0.001080。因此答案為 0.99892-0.00108 = 0.997840。再次強調,這只是一個近似值。實際答案是 0.997856,但推導起來更繁瑣。平均而言,在擲骰子遊戲中決定一個點數後,玩家會多久再提出一個點數?
假設一個點有5/12的機率出現,那麼它將會是6或8,4/12的機率是5或9,3/12的機率是4或10。出現6或8的機率是5/11,出現5或9的機率是4/10,出現4或10的機率是3/9。因此,假設一個點已經成立,那麼出現該點的機率為:(5/12)*(5/11)+(4/12)*(4/10)+(3/12)*(3/9) = 40.61%。
巫師先生,如果50個不同的人把一枚硬幣拋向空中8次,那麼這50個人中,有多少人會連續8次拋出正面或反面?提前謝謝您。
任何一個人拋出8次正面或反面的機率是2*(1/2) 8 = 1/128。如果平均50個人這樣做,其中0.39人會全部拋出正面或反面。至少一個人全部拋出正面或反面的機率是32.44%。
我有一袋100枚硬幣,其中一枚是雙面硬幣。我隨機抽取一枚硬幣,然後觀察它連續拋出10次正面。我抽到雙面硬幣的機率是多少?
這是一道典型的貝葉斯條件機率題。一般來說,給定 B 時 A 的機率是 A 和 B 的機率除以 B 的機率。在本例中,A 是連續投擲 10 次正面,B 是擲出雙頭硬幣。 A 和 B 的機率是 1/100。這是因為擲出雙頭硬幣的機率是 1/100,而如果真的擲出雙頭硬幣,那麼連續拋 10 次正面的機率是 100%。假設隨機擲出一枚硬幣,那麼連續投擲 10 次正面的機率是 (1/100)*1 + (99/100)*(1/2) 10。這是因為擲出雙頭硬幣的機率是 1%,即擲出 10 次正面的機率是 100%,而擲出一枚公平硬幣的機率是 99%,即連續拋出 10 次正面的機率是 (1/2) 10 。因此,假設你連續拋出 10 次正面,那麼你選中兩個正面硬幣的機率為 0.01/(0.01*1 + 0.99* 0.000977) = 0.911843。
您對拋硬幣投注有什麼建議嗎?
是的!我的建議是一開始就押正面朝上。根據科學新聞線上報道,硬幣落地時正面朝上的機率是51%。文章說,原因是拋出的硬幣並非完美地繞軸旋轉,有時看起來像在翻轉,但實際上並沒有。這個假設只適用於硬幣被握在手掌中的情況,這樣硬幣的彈跳就不是問題了。文章也說,旋轉的硬幣落地時反面朝上的機率為80%,因為較重的正面會先向下沉。然而,我對此表示懷疑。我試了20次,得到了11次正面和9次反面。在20次旋轉中,如果成功率為80%,則得到9次或更少反面的機率是1/1775。
我相信我或許能解答旋轉硬幣的問題。十多年前,我在六年級時做過一個關於旋轉硬幣的科學專題。我在《Omni》雜誌上讀到,旋轉硬幣的速度非常快,幾乎總是可以使硬幣反面朝上,因為硬幣的側面是向正面傾斜的。我嘗試了數百次,結果幾乎一致,除了兩次硬幣豎立著的時候。
浪費了好幾個小時後,我終於發現我把它轉得太快了,慢一點就能達到我想要的效果,也就是反面朝上。而且,這枚硬幣也不是完全均勻的,從最薄的部分開始旋轉似乎能增加一致性。幾張滿是胡扯的圖表和一個裝飾成硬幣形狀的巨大紙板圓圈,讓我的科學課得了A,其他課都不及格,因為我完全不做作業。
因此,我已經透過十多年前做過的一個粗略的實驗最終證明,你也許只是在胡思亂想,我幾乎不記得任何事,也沒有真正理解我當時在做什麼。
好吧,我又試了一次,慢慢地把硬幣轉了100次。我說的「慢」是指從彈硬幣到結果顯現的時間至少有兩秒,但不到五秒。我用的是一枚漂亮閃亮的2004-D版硬幣。結果是52次正面,48次反面。所以我還是不相信,無論硬幣以何種速度旋轉,都會出現反面的機率。
我理解的事件「等待時間」是該事件機率的倒數。我感興趣的是計算用一個骰子擲出連續2的等待時間。在模擬中,我平均擲出42次。我該如何將其與擲出連續2的機率連結起來?
對於單一事件,如果機率為 p,則平均等待時間為 1/p,這的確沒錯。然而,對於連續事件,情況會變得更加複雜。設 x 表示最後一次擲出的結果不是 2 的狀態。這也是初始狀態。設 y 表示最後一次擲出的結果為 2 的狀態。第一次擲出結果後,我們有 5/6 的機率仍處於狀態 x,有 1/6 的機率處於狀態 y。設 Ex(x) 表示從狀態 x 開始的擲骰次數的預期,Ex(y) 表示從狀態 y 開始的擲骰次數的預期。那麼…
Ex(x) = 1 + (5/6)*ex(x) + (1/6)*ex(y),且
Ex(y) = 1 + (5/6)*ex(x)
求解這兩個方程式...
Ex(x) = 1 + (5/6)*ex(x) + (1/6)*( 1 + (5/6)*Ex(x))
Ex(x) = 7/6 + (35/36)*Ex(x)
(1/36)*Ex(x)= 7/6
例如(x)= 36 *(7/6)= 42
因此連續兩次擲出 2 的平均等待時間為 42 次。
我遇到了相同類型的問題,只有預期翻轉才能得到兩次正面,在我的數學問題網站上,請參閱問題 128。
假設我們有一個賭博遊戲。一枚無偏硬幣被重複拋擲。每次拋擲,我們需要支付 1 盧比。結果有兩種可能:H 或 T。如果拋出正面和反面的差值為 3,我們將從賭徒那裡得到 8 盧比。我們應該玩這個遊戲嗎?為什麼?我們獲勝的機率是多少?當我們擲出 7 或 9 盧比時,什麼因素會影響獲勝機率?
我們將 x 稱為從起點開始的翻轉預期次數。
如果其中一方的翻轉次數佔多數,則我們將 y 稱為剩餘翻轉的預期次數。
如果一方的翻轉次數佔多數,則我們將 z 稱為剩餘翻轉的預期次數。
E(x) = 1 + E(y)
E(y) = 1 + 0.5*E(x) + 0.5*E(z)
E(z) = 1 + 0.5*E(y)
由此,用矩陣代數很容易得出 E(x) = 9,E(y) = 8,E(z) = 5。因此,平均需要拋擲 9 次才能使正面和反面的機率差達到 3。因此,對於每次拋擲都能贏取 1 盧比的人來說,8 盧比的賭注是一個不錯的選擇,因為他平均能贏取 9 盧比,但只損失 8 盧比。對賭徒來說,賭場優勢是 11.11%。 9 盧比的賭注是公平的,7 盧比的賭注則為 22.22%。
在您2006年3月13日的「問巫師」節目中,您給出了「盧比」遊戲的三個公式。雖然答案在數學上是正確的,但我實在無法理解這三個公式是如何模擬這個問題的。您能解釋一下您是如何得出這三個公式的嗎?
很多人請我進一步解釋一下我的答案。答案需要用到基本的矩陣代數知識。
首先將 x 定義為答案,或直到正面和反面之間的差異為 3 為止的平均翻轉次數。
令 y 為從一側向上翻轉一次的點開始的翻轉預期次數。
令 z 為從一側向上翻轉兩次的點開始的預期翻轉次數。
第一次拋骰子後,其中一方將以一次拋骰子的優勢佔多數。因此 x=1+y。
當任何一方領先一次拋擲時,另一方拋擲的結果要么與初始平局相同,要么是一方領先兩次拋擲。兩種結果的可能性相同。因此 y=1+0.5*x + 0.5*z
當任何一方領先兩次拋擲時,再次拋擲將導致一方領先一次,或遊戲結束。同樣,兩種結果的可能性相同。因此 z=1+0.5*y。
因此我們有三個方程式和三個未知數:
(1)X= 1 + y
(2)Y = 1 + 0.5x + 0.5z
(3)Z = 1 + 0.5y
為了解決這個問題,我們先將最後兩個等式乘以 2 來去掉小數。
(1)X= 1 + y
(2)2Y = 2 + x + z
(3)2Z = 2 + y
我們將 (1) 中的 1+y 代入 (2) 中的 x。
2Y = 2 + 1 + y + z
(4)y=3+z
在 (3) 中不能用 3+z 代替 y
2z = 2 + 3 + z
z = 5
現在用 5 代替 (4) 中的 z 得到
(5)y = 3 + 5 = 8
將 y = 8 代入 (1) 可得
(6)x = 9
一位朋友選擇了一個三次拋硬幣的順序,結果是正面或反面,並讓我選擇我自己的(不同的)三次拋硬幣順序。我們拋一枚公平的硬幣,直到出現我們想要的順序。如果他選擇HHH,我應該選擇哪個順序?在這個賭注中我的優勢是什麼?我該如何根據他選擇的順序來計算該選擇哪個順序?
下表顯示了根據玩家A和玩家B選擇的所有可能模式,玩家A獲勝的機率。
玩家 A 獲勝的機率
| 玩家A | 玩家B | |||||||
| 哈哈哈 | 高血壓 | 高血壓 | 高溫熱電偶 | THH | 甲狀腺激素 | 緊張性甲狀腺功能亢進症 | 時間測試 | |
| 哈哈哈 | 1/2 | 2/5 | 2/5 | 1/8 | 5/12 | 3/10 | 1/2 | |
| 高血壓 | 1/2 | 2/3 | 2/3 | 1/4 | 5/8 | 1/2 | 7/10 | |
| 高血壓 | 3/5 | 1/3 | 1/2 | 1/2 | 1/2 | 3/8 | 7/12 | |
| 高溫熱電偶 | 3/5 | 1/3 | 1/2 | 1/2 | 1/2 | 3/4 | 7/8 | |
| THH | 7/8 | 3/4 | 1/2 | 1/2 | 1/2 | 1/3 | 3/5 | |
| 甲狀腺激素 | 7/12 | 3/8 | 1/2 | 1/2 | 1/2 | 1/3 | 3/5 | |
| 緊張性甲狀腺功能亢進症 | 7/10 | 1/2 | 5/8 | 1/4 | 2/3 | 2/3 | 1/2 | |
| 時間測試 | 1/2 | 3/10 | 5/12 | 1/8 | 2/5 | 2/5 | 1/2 | |
選擇最佳模式的記憶方法是,他的第一和第二個選擇應該分別對應你的第二個和第三個選擇。你的第一個選擇應該與你的第三個選擇相反。例如,如果對手選擇HTT,你的第二個和第三個選擇應該是HT。你的最後一個選擇是T,所以對於HHT模式,你的第一個選擇應該是H。按照這個策略,你的獲勝機率將是2/3到7/8,這取決於對手選擇的模式。
你好,我叫帕蒂。你的網站很棒,而且你看起來知識淵博。你絕對是我在賭場想要的那種人! ! ! !我想知道你能不能幫我。我跟男友說我想在網路上找個問題的答案。如果你能幫我,那我就太有面子了。
我的男友是個錢幣收藏家。他買了一袋小麥幣。我自己對錢幣不太了解。 (他慢慢教我)但他說,他很驚訝那袋錢幣裡竟然沒有某一年份的錢幣,因為這種錢幣太常見了。他說這種事情發生的機率簡直是十億分之一。我告訴他,我會試著問辦公室裡那些自稱天才的人!如果他們不知道,我就試著上網查一下。我偶然遇見了你。
無論如何,如果你能幫忙,我將不勝感激。袋子裡大約有5500枚一分硬幣。美國所有鑄幣廠鑄造的小麥幣一分硬幣總數為242.67億枚。鑄造的1955年版一分硬幣(他要找的那枚)數量是3.3億枚。我辦公室裡的一些人說還有其他因素,例如人口統計,鑄幣廠可能沒有分發所有一分硬幣等等。 …… ...
您的鑄幣數量與Mountain View Coins的鑄幣數量接近。假設所有小麥一分錢入袋的機率相同,那麼任何一分錢硬幣中不是 55 面值的機率為 (24,267,000,000-330,000,000)/24,267,000,000 = 0.986401286。5505 硬幣中的機率可以近似為0.986401286 5500 = 507,033,772,284,213,000,000,000,000,000,000,000 分之一。
我爸爸是個錢幣收藏家,所以我向他尋求了這方面的幫助。他是這樣說的:
這是我的猜測。 1955年,費城鑄造了少量林肯一美分硬幣,但日期卻印了兩次。沒有人知道確切的數量。在發現錯誤之前,它們與其他一美分硬幣混在一起流通。一枚未流通的硬幣如今價值約2000至6000美元。我懷疑那袋「小麥」硬幣裡的所有1955年版硬幣已經被某個尋找雙模硬幣的人全部淘光了。這裡有一張照片: 1955年雙模正面一美分硬幣。
請注意,本網站出售的是「麥穗」版,可以肯定的是,在硬幣被經銷商收集後,一些年份的硬幣已經被剔除。我原本以為那些非雙模版的1955年版硬幣會被歸還收藏,但它們或許會被單獨出售或熔化處理。如今,麥穗版便士中的銅比一美分值錢得多。這就是為什麼他們在幾十年前就改用鍍銅鋅版便士的原因。也有可能,鑄幣廠自己決定不發行許多1955年版硬幣,而是在鑄造後將其熔化處理,以避免人們對稀有的雙模版硬幣產生瘋狂的搶購。鑄幣廠和郵局一直對印刷錯誤感到尷尬,並試圖阻止它們流通。
在您上一篇專欄文章中,您說過「5500 枚硬幣不是 55 的機率可以非常接近地近似為 0.9864012865500 = 507,033,772,284,213,000,000,000,000,000,000,000 分之 100,000,000 分之 100,000 分之 100,000 分之。
我假設「近似」是因為當你處理這5500枚硬幣時,移除的影響是存在的。移除的影響微乎其微!這是一個很好的例子,說明當你移除非目標硬幣時,目標硬幣出現的可能性會降低,因為與不正當遊戲(即目標硬幣被移除)的機率相比,移除的影響非常小。
是的,我說的是“非常接近”,因為世界上的硬幣數量有限。從袋子裡取出一枚非55面值的硬幣,其移除效應會增加袋子裡其他所有硬幣都是55面值的硬幣的機率。如果我沒說“非常接近”,至少會有三個人寫信來糾正我。當然,這只是一個極小的誤差,但我的許多讀者都是完美主義者,即使是最輕微的錯誤,他們也會對我大加指責。
房間裡有兩張桌子。右邊的桌子上有100枚硬幣,其中20枚H面朝上,其餘80枚T面朝上。另一張桌子上沒有硬幣。目標是想辦法移動硬幣,讓兩張桌上H面朝上的硬幣數量相等。房間很暗,你既看不到硬幣,也無法觸摸它們來判斷它們是「朝上」還是「朝下」。
請造訪我的另一個網站 mathproblems.info 尋找解決方案(劇透警告!)
我朋友願意跟我打賭20美元,他給了我3比1的賠率,如果我拋硬幣100次,結果一定是50次正面和50次反面。如果正面和反面都出現,我就贏60美元;如果反面出現,我就欠他20美元。我應該接受這個賭注嗎?另外,如果50/50不是最有可能的結果,還有其他更有可能出現的結果嗎(例如51/49)?
正面和反面正好各出現50次的機率是 (100,50)*(1/2) 100 = 7.96%。公平賠率是11.56比1。因此,3比1的賠率非常糟糕,賭場優勢高達68.2%。這可不是你的朋友。 50/50是正面和反面最有可能出現的機率。一個有趣的賭注是正面/反面的次數是否會在47到53之間。落在這個範圍內的機率是51.59%。如果你能找到一個賭徒押注總數會落在這個範圍之外,那麼在等額投注的情況下,你將獲得3.18%的優勢。
下表顯示了 30 至 70 次正面/反面的機率。
100 次拋擲中全部正面/反面的機率
| 正面/反面 | 可能性 |
|---|---|
| 30、70 | 0.000023 |
| 31, 69 | 0.000052 |
| 32, 68 | 0.000113 |
| 33, 67 | 0.000232 |
| 34, 66 | 0.000458 |
| 35、65 | 0.000864 |
| 36, 64 | 0.001560 |
| 37, 63 | 0.002698 |
| 38, 62 | 0.004473 |
| 39, 61 | 0.007111 |
| 40、60 | 0.010844 |
| 41, 59 | 0.015869 |
| 42, 58 | 0.022292 |
| 43, 57 | 0.030069 |
| 44, 56 | 0.038953 |
| 45,55 | 0.048474 |
| 46, 54 | 0.057958 |
| 47, 53 | 0.066590 |
| 48, 52 | 0.073527 |
| 49, 51 | 0.078029 |
| 50 | 0.079589 |
在 n 次試驗中,w 次獲勝的機率的一般公式為 combin(n,w) × p w × (1-p) (nw) = [n!/(w! × (nw)!] × p w × (1-p) (nw) ,其中每次獲勝的機率為 p 。
如果我拋硬幣 1,000 次,那麼連續看到至少 10 次正面或反面的機率是多少?
你問得真有意思;另一位讀者剛剛給我發了一篇關於這個主題的學術論文。這篇論文包含下圖,顯示機率約為 62%。
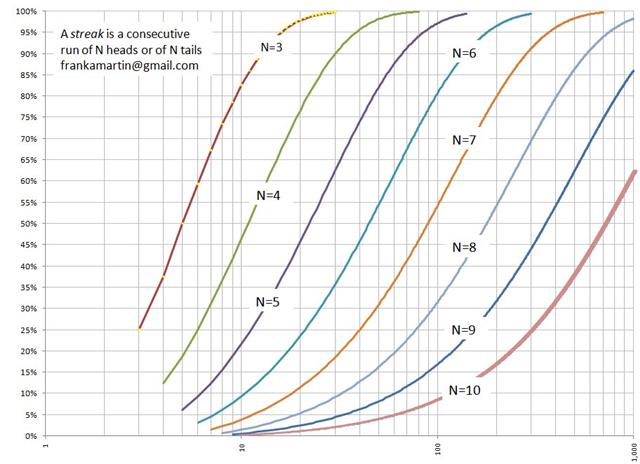
有關該主題的更多信息,請參閱弗蘭克·馬丁 (Frank Martin) 撰寫的《在賭場中遭遇如此糟糕連勝的幾率有多大? 》 (483K)。
如果將一枚硬幣拋 100 次,那麼至少有一次連續出現 7 次正面的機率是多少?
我不知道這個問題是否有一個簡單的、非遞歸的表達式來表達。但是,有一個簡單的遞歸表達式來表示。
f(n)= pr(第一次拋反面的個數)×f(n-1) +
pr(第一次拋擲正面,第二次拋擲反面)×f(n-2) +
pr(前兩次拋擲的正面,第三次拋擲的反面)×f(n-3) +
pr(前三次拋擲的正面,第三次拋擲的反面)×f(n-4) +
pr(前四次拋擲的正面,第四次拋擲的反面)×f(n-5) +
pr(前五次拋擲的正面,第五次拋擲的反面)×f(n-6) +
pr(前六次拋擲的正面,第六次拋擲的反面)×f(n-7) +
pr(前 7 次拋擲的正面次數) =
(1/2)×f(n-1)+
(1/2) 2 ×f(n-2)+
(1/2) 3 ×f(n-3)+
(1/2) 4 ×f(n-4)+
(1/2) 5 ×f(n-5)+
(1/2) 6 ×f(n-6)+
(1/2) 7 × f(n-7) +
(1/2) 7
在哪裡:
f(n)=n次翻轉內成功的機率。
pr(x)=x發生的機率。
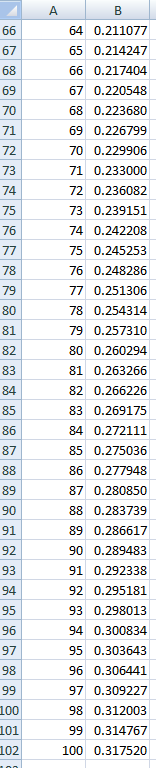
電子表格非常適合解決這類問題。在下面的電子表格截圖中,我在儲存格 B2 到 B8 中輸入了機率 0,因為在 6 次或更少的拋擲次數內不可能連續出現 7 次正面。在儲存格 B9 中,我輸入了以下公式:
=(1/2)*B8+(1/2)^2*B7+(1/2)^3*B6+(1/2)^4*B5+(1/2)^5*B4+(1/2)^6*B3+(1/2)^7*B2+(1/2)^7
然後我把它從單元格B10複製貼上到單元格B102,相當於翻轉100次。這個機率是0.317520。隨機模擬證實了這一點。
 |  |
這篇文章最初發表後,Rick Percy 與我分享了他的矩陣代數解法。以下是我自己的解釋。我假設讀者已經了解矩陣代數的基礎知識。
首先,在任何時候,彈珠台可能處於八種狀態:
p 1 = 成功的機率,假設從當前點開始你需要再擲出 7 個正面。
p 2 = 成功的機率,假設你需要從目前點開始再出現 6 個正面。
p 3 = 成功的機率,假設您需要從當前點開始再出現 5 個正面。
p 4 = 成功的機率,假設您需要從當前點開始再出現 4 個正面。
p 5 = 成功的機率,假設您需要從目前點開始再出現 3 個正面。
p 6 = 成功的機率,假設您需要從當前點開始再出現 2 個正面。
p 7 = 成功的機率,假設您需要從當前點開始再出現 1 個正面。
p 8 = 成功的機率,假設您不需要更多的正面 = 1。
我們將矩陣 S n定義為第 n次翻轉後處於每個狀態的機率。 S 0表示第一次翻轉前的機率,其中有 100% 的機率處於狀態 0。因此 S 0 =
| 1 0 0 0 0 0 0 0 |
設 T 為兩次連續翻轉的變換矩陣,即從 S n到 S n+1 ,其中 S n+1 = T × S n
- 如果您處於狀態 1,那麼在一次翻轉之後,您有 0.5 的機會處於狀態 2(正面),並且有 0.5 的機會保持在狀態 1(反面)。
- 如果您處於狀態 2,那麼在一次翻轉之後,您有 0.5 的機會處於狀態 3(正面),並且有 0.5 的機會返回狀態 1(反面)。
- 如果您處於狀態 3,那麼在一次翻轉之後,您有 0.5 的機會處於狀態 4(正面),並且有 0.5 的機會返回狀態 1(反面)。
- 如果您處於狀態 4,那麼在一次翻轉之後,您有 0.5 的機會處於狀態 5(正面),並且有 0.5 的機會返回狀態 1(反面)。
- 如果您處於狀態 5,那麼在一次翻轉之後,您有 0.5 的機會處於狀態 6(正面),並且有 0.5 的機會返回狀態 1(反面)。
- 如果您處於狀態 6,那麼在一次翻轉之後,您有 0.5 的機會處於狀態 7(正面),並且有 0.5 的機會返回狀態 1(反面)。
- 如果您處於狀態 7,那麼在一次翻轉之後,您有 0.5 的機會處於狀態 8(正面),並且有 0.5 的機會返回狀態 1(反面)。
- 如果您處於狀態 8,那麼您就取得了成功,並且將以 1.0 的機率保持在狀態 8。
將所有這些以轉移矩陣 T = 的形式呈現
| 0.5 0.5 0.0 0.0 0.0 0.0 0.0 0.0 0.0 |
| 0.5 0.0 0.5 0.0 0.0 0.0 0.0 0.0 0.0 |
| 0.5 0.0 0.0 0.5 0.0 0.0 0.0 0.0 0.0 |
| 0.5 0.0 0.0 0.0 0.5 0.0 0.0 0.0 0.0 |
| 0.5 0.0 0.0 0.0 0.0 0.5 0.0 0.0 0.0 |
| 0.5 0.0 0.0 0.0 0.0 0.0 0.5 0.0 0.0 |
| 0.5 0.0 0.0 0.0 0.0 0.0 0.0 0.5 0.0 |
| 0.5 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.5 |
| 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 1.0 |
為了得到一次翻轉後每個狀態的機率...
(1) S1 = S0 ×T
翻轉兩次之後怎麼樣?
(2) S2 = S1 ×T
讓我們用方程式 (2) 來代替方程式 (1)...
(3) S2 = S0 ×T×T= S0 × T2
那麼翻轉 3 次之後呢?
(4) S3 = S2 ×T
將方程式 (3) 代入方程式 (4)...
(5) S3 = S0 × T2 ×T= S0 × T3
我們可以一直這樣做,直到第 100 次翻轉之後的狀態...
S 100 = S 0 × T 100
那麼,T 100是多少呢?在計算機出現之前,要弄清楚這些數字一定非常困難。然而,借助 Excel 的 MMULT 函數,經過大量的複製貼上,我們發現 T 100 =
| 0.342616 0.171999 0.086347 0.043347 0.021761 0.010924 0.005484 0.317520 |
| 0.339863 0.170617 0.085653 0.042999 0.021586 0.010837 0.005440 0.323005 |
| 0.334379 0.167864 0.084271 0.042305 0.021238 0.010662 0.005352 0.333929 |
| 0.323454 0.162380 0.081517 0.040923 0.020544 0.010313 0.005178 0.355690 |
| 0.301693 0.151455 0.076033 0.038170 0.019162 0.009620 0.004829 0.399038 |
| 0.258346 0.129694 0.065109 0.032686 0.016409 0.008237 0.004135 0.485384 |
| 0.171999 0.086347 0.043347 0.021761 0.010924 0.005484 0.002753 0.657384 |
| 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 1.000000 |
右上角的項顯示了翻轉 100 次後處於狀態 8 的機率,即 0.317520。
你聽過一個澳洲板球運動員的故事嗎?他連續35場都預測錯了硬幣,直到第36場比賽才預測正確。這種情況發生的機率有多大?
你提到這件事之前我都沒聽過。你指的是喜鵲隊(Magpies)青少年板球運動員克里斯蒂·佩林(Kristy Perrin)的精彩故事。她確實連續35次拋硬幣預測錯誤。準確預測35次或更多的機率是(1/2) 35 = 34,359,738,368分之一。換個角度來看,中強力球的機率是195,249,054分之一。這比連續35次拋硬幣預測錯誤的可能性高出176倍。
您對拋硬幣投注有什麼建議嗎?
是的!押注拋硬幣者手中朝上的一面。 Persi Diaconis、Susan Holmes 和 Richard Montgomery 合著的學術論文《拋硬幣的動態偏差》得出的結論是,硬幣落地時朝上的機率為 51%。
這個問題是在我的同伴網站Wizard of Vegas的論壇中提出並討論的。
平均而言,在一場50/50的遊戲中,需要多少次嘗試才能連續輸兩次?連續輸3次、4次、n次呢?
我們先來解決兩次損失的情況。
令 x 為從開始或每次獲勝後未來翻轉的預期次數。
令 y 為一次失敗後未來拋擲的預期次數。
我們可以建立以下兩個方程式:
(1)x = 1 + .5x + .5y
一代表玩家必須拋硬幣來改變狀態。獲勝的機率為 50%,保持在狀態 x。失敗的機率為 50%,進入狀態 y。
(2)y = 1 + .5x
再次從狀態 y 開始,1 表示在該點進行翻轉。獲勝的機率為 50%,返回狀態 x。失敗的機率為 50%,遊戲結束,無需再次翻轉,因此隱含的機率為 0.5*0。
將兩個方程式乘以 2 並重新排序可得:
(3)x - y = 2
(4)-x + 2y = 2
將兩個方程式相加可得:
(5)y=4
將其代入 (1) 至 (4) 中的任何方程,得到 x=6。
對於三損失的情況,將三種可能的狀態定義為:
令 x 為從開始或每次獲勝後未來翻轉的預期次數。
令 y 為一次失敗後未來拋擲的預期次數。
令 z 為兩次失敗後未來拋擲的預期次數。
初始方程式為:
x = 1 + .5x + .5y
y = 1 + .5x + .5z
z = 1 + .5x
我們可以將初始狀態設定為矩陣形式:
| 0.5 | -0.5 | 0 | 1 |
| -0.5 | 1 | -0.5 | 1 |
| -0.5 | 0 | 1 | 1 |
如果你還記得矩陣代數,我們可以用行列式(A)/行列式(B)來解 x,其中
A =
| 1 | -0.5 | 0 |
| 1 | 1 | -0.5 |
| 1 | 0 | 1 |
B =
| 0.5 | -0.5 | 0 |
| -0.5 | 1 | -0.5 |
| -0.5 | 0 | 1 |
| 0.5 | -0.5 | 0 |
| -0.5 | 1 | -0.5 |
| -0.5 | 0 | 1 |
Excel 有一個方便的行列式函數:=mdeterm(range)。在本例中,x = mdeterm(矩陣 A)/mdeterm(矩陣 B) = 1.75/0.125 = 14。
我們可以使用遞歸來處理更多連續失敗的情況。假設是 4 次。根據上文所述,平均需要拋硬幣 14 次才能連續失敗 3 次。此時,硬幣將再次拋出,重新開始的機率為 50%。因此:
x = 14 + 1 + x/2
x/2 = 15
x = 30
換句話說,在前一個答案上加一,然後加倍。
不難看出其中的規律。連續 n 次失敗的期望拋擲次數是 2 n+1 -2。
這個問題是在我的「拉斯維加斯巫師」論壇上提出並討論的。
假設一枚公平硬幣被拋擲 n 次,出現至少一次 t 次反面的機率是多少?
答案是 1-F (t) n+2 /2 n ,其中 F (t) n是 t 步斐波那契數列中的第 n 個數字。
你可能會問,斐波那契數列是什麼?它的第一個數字是 1。在 t 步驟序列中,每個後續數字都是前 t 個數字總和。假設第一個數字之前的任何數字都是 0。
讓我們來看一個兩步序列。第一個數字是 1。第二個數字是前兩個數字總和。假設 1 前面有 0,所以第二個數字是 0+1=1。第三個數字是 1+1=2,第四個數字是 1+2=3,第五個數字是 2+3=5。
前十二個二步斐波那契數列為:1、1、2、3、5、8、13、21、34、55、89、144。
我們舉個例子,拋十次硬幣,至少有一次連續擲出兩次反面的機率是多少?
我們使用兩步驟斐波那契數列,因為我們只需要兩次反面。數列中的第 12 個數字(比翻轉次數多 2 個)是 144。因此,答案是 1-F (2) 10+2 /2 10 = 1 - 144/2 10 = 1 - 144/1024 = 85.94%。
在 20 次拋擲中,連續出現 5 次反面的機率是多少?
前 22 個 5 步斐波那契數列為 1、1、2、4、8、16、31、61、120、236、464、912、1793、3525、6930、13624、26784、52656、10351930、13624、26784、52656、103519626206462620620620626206206206206206206262620620620696206。
因此答案為 1 - F (5) 20+2 /2 20 = 1 - 786,568/1,048,576 = 1 - 75.01% = 24.99%。
我在Wizard of Vegas論壇上討論過這個問題。
有一枚偏差的硬幣,正面朝上的機率為 60%。它被拋擲,直到連續出現兩次正面或兩次反面。先出現兩次正面的機率是多少?
這是答案和解決方案(PDF)。
有關此問題的討論,請訪問我在Wizard of Vegas 的論壇。
巫師,我向你挑戰一個賭注。規則如下:
- 你可以選擇任何你喜歡的正面(H)和反面(T)的圖案。例如,HTT。
- 在揭示你的圖案後,我會選擇我的。
- 我們會重複拋硬幣,直到出現一種圖案。選擇該圖案的人獲勝。
- 我給你 3 比 2 的賠率。
你接受嗎?我願意做多少次就做多少次。
不。不過,嘗試得不錯。後手擁有巨大的位置優勢。以下是後手的策略及其獲勝機率。
Odiusgambit 遊戲策略
| 玩家 1 | 玩家 2 | Pr. 玩家 2 獲勝 |
|---|---|---|
| 哈哈哈 | THH | 87.50% |
| 高血壓 | THH | 75.00% |
| 高血壓 | 高血壓 | 66.67% |
| 高血壓 | THH | 75.00% |
| THH | 高溫熱電偶 | 75.00% |
| 甲狀腺激素 | 緊張性甲狀腺功能亢進症 | 66.67% |
| 緊張性甲狀腺功能亢進症 | 高溫熱電偶 | 75.00% |
| 時間測試 | 高溫熱電偶 | 87.50% |
如上表所示,我獲勝的最佳機會(或您獲勝的最差機會)是選擇 THT 或 HTH,此時我的獲勝機會仍然只有 1/3。我應該以 2 比 1 的賠率進行公平投注,因此如果只以 3 比 2 的賠率進行投注,那麼您的優勢就有 16.67%。
以下是記住玩家二策略的方法。令 P(x) 表示玩家一在位置 x 的選擇。令 O(x) 表示玩家一在位置 x 的選擇的反方向。玩家二的選擇應該永遠是:O(2) - P(1) - P(2)。
我在Wizard of Vegas論壇上提出並討論了這個問題。
如果拋一枚公平硬幣40次,出現5次正面和5次反面的機率是多少? 「1連」表示至少出現1次正面,「5連」表示至少出現5次反面。正面和反面的連次不必相鄰。
請點擊下面的按鈕以取得答案。
這是我的解決方案(PDF)。
我在Wizard of Vegas論壇上提出並討論了這個問題。
亨利和湯姆決定賭一把拋硬幣。亨利擲正面贏,湯姆擲反面贏。
每次拋硬幣要1美元,他們實在無聊,所以決定拋一百萬次。每次拋完後,輸的人會給贏的人一張支票,作為最終的餘額。支票金額的期望值是多少?
答案的一般公式是 sqrt(方差 * (2/pi))。
在這種情況下,變異數為 1,000,000。因此,實際結果與預期結果之間的預期絕對差為 sqrt(1,000,000 × (2/pi)) =~ 797.884560802865355587989211986876373695171726 232986931533185165934131585179860367700250466 781461387286060511772527036537102198390911167 448599242546125101541269054116544099863512903 26916150611945072854641673391869565434059837 28381269120656178667772134093073。
我在Ask the Wizard #358中提出了一個相關問題,這將有助於顯示我從哪裡得到 sqrt(2/pi) 項。
這個問題是在Wizard of Vegas論壇上提出並討論的。
假設一家賭場有一款基於公平拋硬幣的遊戲,賠率相同。一位玩家希望以每次1美元的賭注玩一百萬次。他應該投入多少錢才能有50%的機率不破產?
讓我們先回答這個問題:假設玩家的資金無限,那麼在一百萬次拋擲之後,玩家虧損超過 x 個單位的機率是多少。
由於這是一個公平的賭注,一百萬次拋擲後的平均贏利為零。每次拋擲的變異數為1,因此一百萬次拋擲的變異數為一百萬。因此,一個標準差為 sqrt(1,000,000) = 1000。
我們可以使用 Excel 函數 =norm.inv(probability,mean,standard deviation) 來計算所需的資金。例如,如果我們輸入 =norm.inv(.25,0,1000),我們會得到 -674.49。這意味著,如果在一百萬次拋擲之後,玩家有 25% 的機率輸掉 674 或更多。請記住,這只是一個估計值。為了得到正確的答案,我們應該使用二項分佈,但如果拋擲了一百萬次,這將非常繁瑣。
如果玩家帶著674美元上桌,他很可能在百萬翻倍前就把錢花光。如果他能繼續賒賬,他或許能翻盤,最後輸掉的錢少於674美元。事實上,一旦玩家的賠率是-674美元,那麼在未來的某個時間點,他最終輸掉的錢有一半的可能性會高於或低於-674美元。
因此,如果玩家可以賒帳玩,則可能出現三種結果。
- 玩家的等級永遠不會低於-674。
- 玩家在某個時刻跌至 -674 以下,但恢復並最終超過 -674。
- 玩家在某個時刻跌至 -674 以下,繼續玩並輸得更多。
我們已經確定情境 3 的機率為 25%。
場景 2 的機率必須與場景 3 的機率相同,因為一旦玩家落後 -674,那麼在一百萬次拋擲之後,他有 50% 的機會達到或低於該點。
場景 1 是唯一的其他選擇,其機率必須為 100%-25%-25% = 50%。
如果玩家永遠不會低於 674 的機率是 50%,那麼低於該金額的機率一定是 100%-50% = 50%。
因此,我們對原始問題的答案是 674 美元。
我在Wizard of Vegas論壇上提出並討論了這個問題。


