概率 - 牌
我在網路上玩百家樂,75 手牌中莊家贏了 52 手,閒家贏了 23 手。差額為 29,發生這種情況的機率是多少?
首先,我假設您不計算平局。換句話說,您的意思是 75 手牌不平手。 75 手牌不平手的可能性非常小。在 75 手牌中,莊家獲勝的預期次數為 38.00913745。標準差是 75、莊家獲勝機率和閒家獲勝機率乘積的平方根。假設沒有平局,莊家獲勝的機率為 0.506788499,閒家獲勝的機率為 0.493211501。因此,標準差為 4.329727904。然後,您必須對二項分佈進行半點修正,並在標準常態分佈表中尋找 Z 統計量(此步驟留給讀者)。最終答案是,莊家贏 52 次或以上的機率是 0.0009。您的問題也考慮了莊家贏 23 次或更少(也相差 29 次或更多)的可能性,這個機率是 0.0004。所以最終答案是,相差 29 次或更多的機率是 0.0013,即 769 分之一。
當我計算加勒比海梭哈撲克玩家與莊家手牌的組合數時,僅得到3,986,646,103,440種,而您的結果卻是19...等,相差正好5倍。我使用了組合函數(52,5)*組合函數(47,5)。請問我的計算哪裡出錯了?感謝您,我認為您的網站非常出色。
感謝您的讚美。您的計算少了五倍,因為莊家可以任意一張牌面朝上。換句話說,莊家的手牌順序確實重要,因為第一張牌是明牌。正確的總組合數推導應為combin(52,5)*47*combin(46,4) = 19,933,230,517,200。
抽三張牌拿到對⼦與抽五張牌撲克拿到full house葫蘆的概率是多少?
在這種狀況拿到full house葫蘆有兩種⽅式: (1)抽到三條、或者(2)對⼦再抽到⼀張同點數牌、還有另⼀個對⼦。我將假設你會捨棄三張各⾃不同的單牌。 ⾸先, 讓我們先從(1)的排列組合總數著⼿算起。那裡只剩下3種花⾊的3種點數牌(記住你已經捨棄3張各⾃不同的單牌)、4種花⾊的9種點數牌。其排列組合總數為 3*combin(3,3)+9*combin(4,3) = 3*1 + 9*4 = 39. 接下來, 讓我們算⼀下(2)狀況的排列組合總數。從既有對⼦再加上⼀張相同點數牌、還剩下有2張牌。剩餘的3張牌當中形成3種點數的對⼦有combin(3,2)種⽅式, 剩餘的4張牌當中再形成⼀個對⼦有combin(4,2)種⽅式。所以在(2)的排列組合總數為 2*(3*combin(3,2)+9*combin(4,2)) =2*(3*3 + 9*6) = 126. 在(1)與(2)狀況之下形成full house葫蘆的⽅式總和為39+126=165. 第⼆輪抽牌要從3張牌選取的⽅式有combin(47,3)=16,215種。拿到full house葫蘆的機率為抽牌⽅式除以排列組合總數, 為165/16,215 = 0.0101758, 或者差不多是98分之⼀。 欲知combin()函數的更多資訊, 請參閱我的 撲克中的機率 專⾴。
我每週會和朋友玩⼀次撲克(五張牌梭哈、七張牌梭哈)。我們同桌共有七位玩家。隨著玩家⼈數的增多、從單副52張牌組當中拿到牌⾯的機率似乎就會驟減。你是否有數學上的公式可以指引我?
沒有, 無論賭桌上有多少位玩家、拿到給定牌⾯的機率都是相同的。沒⾒到的牌就是⼀張沒出現的牌, 不管那張牌是被另⼀位玩家拿到或者還藏在牌組當中。
最近有人告訴我一個難以置信的故事! !我的一個朋友告訴我,當他家玩撲克牌友誼賽時,他和他的朋友在同一手牌中都抽到了順子,而且沒有抽任何牌! ! (五張牌抽牌)我覺得這難以置信,我從你們的網站上計算出,抽到順子的機率大約是65000比1,那麼在6個人一起玩(沒有抽任何牌)的情況下,一手牌中抽到2張順子的機率是多少呢?
在三張牌撲克中,如何計算出獲得以下牌型的機率:(1)Q 高牌、(2)K 高牌、(3)A 高牌?
我將先計算出 K 高牌,然後簡單展示其他兩個牌型的公式。機率是 K 高牌的數量除以牌型總數。小於 K 的牌型數為 11。 K 高牌必須有兩個不同的等級。從 11 張牌中排列 2 張的方法數為combin (11,2) = 55。但是,其中一個組合是 K-Q-J,可以組成順子,因此減去該組合,剩下 54 個不能組成順子的組合。接下來,每個等級有四種花色,即 4 3 =64 種可能的花色組合。但是,這 64 種花色中有四種可以組成同花,因此剩下 64-4=60 種花色組合。因此,K 高牌的組合總數為 54*60=3240。從 52 張牌中排列 3 張,總共有 combin(52,3)=22,100。因此,組成 K 高牌的機率為 3,240/22,100 = 0.1466063。組成 A 高牌的機率為:(combin(12,2)-2)*(4 3 -4)/combin(52,3)=0.1737557。請注意,由於 a-2-3 和 qka 順子的存在,所以這裡用 -2 而不是 -1。
皇后高牌的機率為:(combin(10,2)-1)*(4 3 -4)/combin(52,3)=0.119457。
拿皇家同花順的機率是多少?拿連續皇家同花順(順著或逆著)的機率是多少?
皇家同花順的機率等於可能的皇家牌數(每種花色各一張)除以從52張牌中選出5張的方式數,即combin (52,5)=2,598,960。因此,答案是4/2,598,960 = 0.00000153908,即649,740分之一。
連續同花大順的機率等於(花色數)*(方向數)/(52 張牌中 5 張牌的排列組合總數)= 4 * 2 /排列(52,5) = 8 / 311,875,200 = 8 / 可能的同花大順數量(即 4 張(每種花牌)分別乘以一張花牌的方向數5 5 5 5張牌的組合方式數,即排列(52,5) = 311,875,200。因此,答案為 4/311,875,200 = 0.00000002565,即 38,984,400 分之一。
我喜歡用美元玩「說謊者撲克」遊戲。請問一張鈔票上出現任一個相同數字的機率是多少?謝謝。如果我和三個人一起玩,任何一個數字出現的機率是多少?
首先,讓我來回答一個未被提及的問題:某個特定數字在一張隨機鈔票上出現 n 次的機率。一張鈔票上有 8 位數字,因此特定數字出現 n 次的機率為 combin(8,n)*0.1 n *0.9 8-n /10 8 。下表顯示了特定數字出現 0 到 8 次的機率。
騙子撲克中的特定數字賠率
| 數位 | 可能性 |
|---|---|
| 8 | 0.00000001 |
| 7 | 0.00000072 |
| 6 | 0.00002268 |
| 5 | 0.00040824 |
| 4 | 0.00459270 |
| 3 | 0.03306744 |
| 2 | 0.14880348 |
| 1 | 0.38263752 |
| 0 | 0.43046721 |
| 全部的 | 1.00000000 |
下表列出了每種可能出現的鈔票類型的機率,按每種類型的數量分類。例如,序號 66847680 的鈔票可能出現一張三張同點鈔票、一張對子鈔票和三張單張鈔票,機率為 0.1693440。
說謊者撲克中的一般機率
| 8 橡木 | 7 橡木 | 6 橡木 | 5 橡木 | 4 橡木 | 3 橡木 | 2 橡木 | 1 橡木 | 可能性 |
|---|---|---|---|---|---|---|---|---|
| 1 | 0.0000001 | |||||||
| 1 | 1 | 0.0000072 | ||||||
| 1 | 1 | 0.0000252 | ||||||
| 1 | 2 | 0.0002016 | ||||||
| 1 | 1 | 0.0000504 | ||||||
| 1 | 1 | 1 | 0.0012096 | |||||
| 1 | 3 | 0.0028224 | ||||||
| 2 | 0.0000315 | |||||||
| 1 | 1 | 1 | 0.0020160 | |||||
| 1 | 2 | 0.0015120 | ||||||
| 1 | 1 | 2 | 0.0211680 | |||||
| 1 | 4 | 0.0211680 | ||||||
| 2 | 1 | 0.0020160 | ||||||
| 2 | 2 | 0.0141120 | ||||||
| 1 | 2 | 1 | 0.0423360 | |||||
| 1 | 1 | 3 | 0.1693440 | |||||
| 1 | 5 | 0.0846720 | ||||||
| 4 | 0.0052920 | |||||||
| 3 | 2 | 0.1270080 | ||||||
| 2 | 4 | 0.3175200 | ||||||
| 1 | 6 | 0.1693440 | ||||||
| 8 | 0.0181440 | |||||||
| 全部的 | 1.0000000 | |||||||
橡木 = “一種”
欲了解更多信息,請參閱我的“騙子撲克”頁面。
用一副 52 張牌的撲克牌,抽出一對 J 的機率是多少?
假設您抽五張牌,而所有牌中剛好有兩張 J,那麼機率就是 combin(4,2)*combin(48,3)/combin(52,5) = 6*17296/2598960 = 3.99%。
在牌九撲克拿到三對的機率是多少?這個機率比三條大還是小?
不算三條和兩對,以下是湊成三對的方式和組合數。
沒有通配符:combin(13,3)*10*6 3 *4 =2471040
百搭牌用來對抗一對 A:combin(12,2)*10*6 2 *4 2 = 380,160
外卡用作單張 A 牌:combin(12,3)*6 3 = 47,520
總組合數為 2,898,720。這還不到三條組合數(747,0676)的一半。
根據你的公式,皇家同花順的賠率是4/2,598,960 = 1/649,740。所以,如果我和莊家一對一玩加勒比梭哈,我的牌和莊家的牌的和應該相等,即649,740*2=1,299,480。因此,根據數學計算,1,299,480手牌之後應該會出現兩手皇家同花順。請告訴我我是否理解正確。
你說得對,平均每649,740手牌中會出現一次皇家同花順,而1,299,480手牌中皇家同花順的預期出現次數是2次。然而,這只是平均值。每一手牌過去,你距離拿到皇家同花順都只有一步之遙。每局獨立試驗都具有這種無記憶特性,所以皇家同花順永遠不會過期。
在 1,299,480 手牌中出現零張王室牌的機率為 13.53%。
您好,我是牌九撲克的常客,我注意到您的網站上有很多關於這個遊戲的精彩資訊。前幾天我和一個朋友玩牌九,他拿到了一手9高牌,我認為這是最低的牌型了。我玩牌九這麼多年,只見過一次這種情況。五手牌之後,他又拿到了一副一樣的牌(2-3-4-5-7-8-9)。我們簡直不敢相信,也很好奇這種情況發生的機率有多大,所以想問您。感謝您抽出時間,也感謝您精彩的網站。
形成9高牌的排列方式有兩種,一種是您提到的,另一種是2-3-4-6-7-8-9。無法形成同花的花色組合數為4 7 -4*(combin(7,5)*3^2+6*3+1) = 15,552。因此,9高牌的機率為2*15,552/combin(53,7) = 31,104/154,143,080,即9,911分之一。如果您只玩五次,獲得兩手9高牌的機率為9,826,685分之一。我認為這種情況只是巧合,而不是隨機數產生器或程式編碼的故障。
我的問題是關於賭場戰爭中尼加拉賭場規則中莊家優勢和風險因素的計算(例如,加註時賠付3-1,輸掉原始賭注)。您是如何得出這些數字的?我現在正在嘗試計算它們。我遇到麻煩了。感謝您的協助。
假設 d 為牌組數。第一輪平手的機率為 (4*d-1)/(52*d-1)= 0.073955。第二輪平手的機率為 12*4*d/(52*d-2)*(4*d-1)/(52*d-3)+(4*d-2)/(52*d-2)*(4*d-3)/(52*d-3) = 0.073974。設 p 1為第一輪平手的機率,p 2為第二輪平手的機率。則玩家回報為 p 1 *(2*p 2 +(1-p 2 )/2*(1-2))= -0.023301。乘以 -1,則莊家優勢為 2.33%。我希望我沒有太快地回顧這一點。
可以告訴我加勒比海地區19,933,230,517,200種組合數是怎麼算出來的嗎?我依照你的五張牌撲克組合數算出了2,598,960種組合數。接下來我該怎麼繼續呢?先謝謝了。
您正確計算了玩家組合數: combin (52,5)=2,598,960。由此推算,莊家可能的組合數為 combin(47,5)=1,533,939 種。然後,五張莊家牌中任一張都可以正面朝上。因此,2,598,960*1,533,959*5=19,933,230,517,200 種組合數。
首先,我想說,我覺得您的網站真的很棒。我已經告訴了幾個人,希望他們也能試試看。祝您繼續成功。我也很喜歡 WinPoker 的連結。我非常喜歡 WinPoker,所以訂購了它。這是一個很棒的程式。我有一個問題希望您能幫助我。我一直在嘗試計算七張牌梭哈中每手牌出現的次數。我有一份您的七張牌表,但我對計算這些數字的數學原理很感興趣。我能計算出五張牌的數字,但七張牌的數字讓我很困惑。我想發送一個包含我的數字的 Excel 2000 檔案。我還想知道如何計算一副 53 張牌、帶有百搭牌的撲克牌中的順子數量。救命! ! !
謝謝你的讚美。我同意七張牌梭哈的點數計算起來很難。所以我用電腦來算。我的程式會計算所有可能的組合,並為每個組合評分。牌九撲克中的百搭順子數量是 11*(4 4 -4)+10*3*(4 4 -4)=10332。加上 10200 個自然順子,總數是 20532。
我了解加勒比梭哈撲克或Let it Ride牌桌上任何一個人拿到皇家同花順的機率,以及這些機率是如何計算出來的。但我的問題是:身為旁觀者,在任何特定牌局中,看到牌桌上任何一位玩家拿到這些牌的機率是多少?我相信這取決於牌局數量……難道只是個人的機率乘以牌局數量?例如,如果牌桌上有4位玩家,看到任何一手牌拿到皇家同花順,就代表拿到皇家同花順的機率是4倍嗎?我有點困惑!
你的方法近似效果不錯。然而,按照這個邏輯,拋硬幣時,每3個人中至少有一個人拋出正面的機率是3*50%=150%。假設事件獨立,n次試驗中至少有一次成功的機率(每次成功的機率為p)是1-(1-p) n 。在拋硬幣的例子中,這個機率是1-0.5 3 =0.875。在四人玩加勒比梭哈撲克的情況下,至少有一次出現同花大順的機率是1-(1-4/2598960) 4 = 0.00000615629。然而,由於所有牌都來自同一副牌,因此事件並非獨立事件。確定確切的正確答案需要非常複雜的數學計算,而近似值應該非常接近正確答案。
在牌九撲克中,拿到七張自然同花順的機率是多少?我在賭場工作,15年來第一次遇到這種情況。那位幸運的顧客贏了4萬美元。
自然同花順共有 32 種可能(4 個等級乘以 8 種可能的 7 張牌組合)。從 53 張牌中抽出 7 張牌的可能組合共有 combin(53,7) = 154143080 種。因此答案是 32/154143080,即 4816971 分之 1。
在三張牌撲克中連續兩手獲得相同的同花順(等級和花色)的機率是多少?
第一手牌拿到同花順的機率是 4*12/combin(52,3) = 48/22100 =~ 0.0022。下一手牌拿到完全相同的機率是 1/22100。所以答案是 (48/22100)*(1/22100) = 48/488410000,即 1/10,175,208。這比中 6/49 彩票的機率高出 1.37 倍,後者的機率是 1/13983816。
在一副 8 副牌的百家樂中,玩家和莊家在同一筆牌中同時獲得一張 A 和一張方塊 8 的機率是多少?
(8 2 /combin(416,2))* (7 2 /combin(414,2)) = 0.00000043,或 2308093 中的 1
我最近目睹了一件奇怪的事。我當時正在觀看一場五張牌的撲克遊戲,最多只能抽兩張牌。一位玩家抽了一張牌,湊成了紅桃同花。莊家抽了一張牌,湊成了黑桃同花。當然,莊家的同花牌更大。遊戲中還有另外三位玩家。同一手牌中出現兩張同花的機率是多少?
讓我們定義同花的機率,也就是發牌時拿到一張牌,或是抽到四張同花。為了簡單起見,我們假設玩家抽到一對或順子,並且抽到四張同花。發牌時拿到同花(不含順子/皇家同花)的機率是 4*(combin(13,5)-10)/combin(52,5) = 5108/2598960 = 0.0019654。拿到四張同花的機率是 4*3*combin(13,4)*13/combin(52,5) = 111540/2598960 = 0.0429172。抽到同花的機率是 9/47。因此,拿到四張同花並完成的總體機率為 0.0429172*(9/47) = 0.0082182。因此,拿到同花的總機率為 0.0019654 + 0.0082182 = 0.0101836。5 位玩家中剛好有 2 位拿到同花的機率為 combin(5,2) * 0.0101836 2 *(1-0.0101836) * 0.0160901090109019010901901901901901909019009090969。
我想知道在五人玩一副牌的七張牌梭哈遊戲中,有人拿到四張同花的機率是多少?希望您能幫助我,謝謝您的寶貴時間。
從 52 張牌中抽出 7 張,總共有 combin(52,7)=133,784,560 種排列方式。包含四張同點牌的 7 張牌組合的數量為 13*combin(48,3) = 224,848。13 表示四張同點牌的點數,combin(48,3) 表示從剩下的 48 張牌中抽出 3 張的排列方式數。因此,機率為 224,848/133,784,560 = 0.0017,即 595 分之一。
當你打開一副新的牌時,每副牌的花色都是從A到K。將一副洗好的牌重新洗回原來的A到K狀態,機率是多少?
52 階乘中的 1,或80,658,175,170,943,900,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000
如果十個人從一副牌中每人得到兩張牌,那麼兩個玩家拿到一對 A 的機率是多少?
首先,從 10 名玩家中選出 2 名玩家,共有 10*9/2=45 種方法。其中兩位特定玩家拿到四張 A 的機率為 1/combin(52,4)=1/270725。因此,任兩位玩家拿到一對 A 的機率為 45/270725=0.0001662。
如果七名玩家每人拿到七張牌,那麼至少有一人拿到 7 張同花牌的機率是多少?
單一玩家獲得 7 張同花牌的機率為 4*combin(13,7)/combin(52,7) = 1/19491。7 個玩家中至少有一名玩家獲得 7 張同花牌的機率約為 2785 分之一。
我知道從數學上來說一切皆有可能,但前幾天晚上在賭場,我好像目睹了十億分之一機率的事情,當然,這種事也並非從未發生過。事情是這樣的:在「放馬過來」的賭桌上,40手牌(40張單張三張牌,大約8輪,5人參與)中,有3張四條。四條的機率大約是4100比1,那麼在40手牌中出現三張四條的機率是多少?請回答,這簡直要把我逼瘋了。我是老粉絲了。
為簡單起見,我們假設每手牌都是從一副新牌中發出的。四條的機率是 13*48/combin(52,5) = 624/2598960。40 張四條中恰好出現 3 張的機率是 combin(40,3)*p 3 *(1-p) 37 = 1/7378135,其中 p = 3 *(1-p) 37 = 1/7378135,其中 p = 624/25960。所以這更像是七百萬分之一的機率。
首先,我想告訴你,我非常喜歡你的網站,也非常欽佩你的數學能力。我用6副牌來發21點,還加了3張百搭牌,原因我就不多說了,不過,連續發3張百搭牌給一個玩家的機率是多少?非常感謝。
不客氣,謝謝你的讚美。從六副牌的牌盒中連續發出三張百搭牌(加上三張百搭牌)的機率是 1/combin(315,3) = 1/5,159,805。另一個解是 (3/315)*(2/314)*(1/313)。
用一副52張的牌,給四個玩家每人發13張牌,四個玩家都拿到了從A到2的順子,那麼這四個玩家的機率是多少?這些牌不必是同一花色。
答案是 (4 13 /COMBIN(52,13))* (3 13 /COMBIN(39,13))* (2 13 /COMBIN(26,13)) = 1/61,204,166,001。
發到四張皇家牌的機率是多少?
皇家牌有四種可能的花色。有五張牌可能缺失。第五張牌可能是其他47張牌中的一張。因此,皇家牌共有4*5*47=940種組合方式。組合方式共有(52,5) = 2,598,960種。因此,機率為940/2,598,960 = 2,765分之一。
親愛的小伙子,假設洗了一副52張牌,我們隨機抽出18張,分成6堆,每堆3張。請問其中一堆剛好包含3張(4張中的3張)A的機率是多少?
解決這個問題的簡單方法是,第一堆牌中有三張 A 的機率是 (4/52)*(3/51)*(2/50) = 1/5525。然而,每堆牌中有三張 A 的機率相同,所以我們乘以 6,得到 6/5525 = 0.001086
在五張牌梭哈遊戲中拿到所有面牌的機率是多少?
(12/52)*(11/51)*(10/50)*(9/49)*(8/48) = 0.00030474,或約 3282 分之 1。
在玩 Let it Ride 遊戲的兩個小時內獲得兩張四條的機率是多少?
任何一手牌中出現四條的機率為 13*48/combin(52,5) = 0.0002401。假設你在兩小時內可以玩 120 手牌。那麼恰好出現兩張四條的機率為:combin(120,2) × 0.0002401 (2 × (1-0.0002401) 118 = 0.000400095 = 1/2499.41。
在四張牌撲克中,順子和同花哪個更有可能?
不算同花順和皇家同花順,順子的機率是1.02%,同花的機率是1.04%。所以同花的機率略高一些。
在100萬手牌中,出現20萬手大同花順荒的機率是多少?我對答案本身更感興趣。
我很少這麼說,但我試了幾個小時,但這個問題的數學計算實在太難了。所以我向我的朋友、數學教授加博爾·梅傑西(Gabor Megyesi)求助。這是他解決任何「乾旱」問題的公式。
- 設 p 為贏得任何一手牌的機率。
- 設 d 為乾旱持續時間。
- 設 n 為玩過的牌數。
- 設 k=dp 和 x=np。
- 若 k=1,則令 a=-1,否則求 a 使得 k=-ln(-a)/(1+a)。 (a 為負數,如果 k>1,則 -1 < a < 0,如果 k < 1,則 a < -1,且 a 需要高精度計算。)[嚮導註:此類解法可在 Excel 中使用工具選單下的「目標求解」功能輕鬆找到。 ]
- 若 k=1 則令 A=2,否則令 A=(1+a)/(1+ak)。
- n 年間不發生長度為 d 的乾旱的機率約為 Ae a x 。
在這個特定問題中,p=1/40391,d=200000,n=1000000,k=4.9516,x=24.758,a=-0.0073337,A=1.03007。因此,不發生乾旱的機率為 1.03007*e -0.0073337*24.758 = 0.859042。因此,至少發生一次乾旱的機率為 1-0.859042 = 0.140958。
這是 Gabor Megyesi 的完整5 頁解決方案(PDF)。感謝 Gábor 的幫助。
我隨機模擬了32095組一百萬手牌,其中至少出現一次乾旱的號碼是4558,機率為14.20%。
假設你從不同的牌堆中發出兩手五張牌的撲克牌。你被告知A手牌至少包含一張A。你被告知B手牌包含一張黑桃A。哪一手牌更有可能包含至少一張A?
下表顯示了完全隨機的一手牌中出現 0 到 4 張 A 的機率。
Ace 機率 — 隨機手牌
| 王牌 | 公式 | 組合 | 可能性 |
|---|---|---|---|
| 0 | 合併(48,5) | 1712304 | 0.658842 |
| 1 | 組合(4,1)×組合(48,4) | 778320 | 0.299474 |
| 2 | 組合(4,2)×組合(48,3) | 103776 | 0.03993 |
| 3 | 組合(4,3)×組合(48,2) | 4512 | 0.001736 |
| 4 | 組合(4,4)×組合(48,1) | 四十八 | 0.000018 |
| 全部的 | 2598960 | 1 |
對 1 到 4 張 A 牌進行求和,我們發現至少出現一張 A 牌的機率為 0.341158。出現兩張或兩張以上 A 牌的機率為 0.041684。
假設至少有一張 A,那麼再出現一張 A 的機率可以用貝葉斯定理重新表述為機率(至少有一張 A 的情況下再出現兩張 A)= 機率(兩張或更多張 A)/機率(至少有一張 A)= 0.041684/ 0.341158 = 0.122185。
對於那些不熟悉貝葉斯定理的人來說,它指出給定 B 時 A 的機率等於 A 和 B 的機率除以 B 的機率,或 Pr(A 給定 B) = Pr(A 和 B)/Pr(B)。
下表顯示了從牌堆中移除黑桃 A 後,其他 A 的每個數量的組合和機率。
A 機率 — 移除 A 牌
| 王牌 | 公式 | 組合 | 可能性 |
|---|---|---|---|
| 0 | 組合(3,0)×組合(48,4) | 194580 | 0.778631 |
| 1 | 組合(3,1)×組合(48,3) | 51888 | 0.207635 |
| 2 | 組合(3,2)×組合(48,2) | 3384 | 0.013541 |
| 3 | 組合(3,3)×組合(48,1) | 四十八 | 0.000192 |
| 全部的 | 249900 | 1 |
這表示至少再出現一張 A 的機率為 0.221369。
為了好玩,我們用貝葉斯定理來解答同樣的問題。假設隨機發牌,直到找到一手包含黑桃 A 的牌。假設牌中包含黑桃 A,那麼至少再出現一張 A 的機率可以改寫為機率(假設手中有黑桃 A,則至少有兩張 A)。根據貝葉斯定理,這等於機率(手中有黑桃 A 且至少還有一張 A)/機率(手中有黑桃 A)。我們可以將分子分解為機率(包括黑桃 A 在內的 2 張 A)+機率(包括黑桃 A 在內的 3 張 A)+機率(4 張 A)。使用第一個表格,這等於 0.039930×(2/4) + 0.001736×(3/4) + 0.000018 = 0.021285。出現黑桃A的機率為5/52 = 0.096154。因此,給定黑桃A,至少出現兩張A的機率為0.021285/0.096154 = 0.221369。
因此,如果至少有一張 A,則出現兩張或兩張以上 A 的機率為 12.22%,如果是黑桃 A,則出現兩張或兩張以上 A 的機率為 22.14%。
好吧,我相信你的數字,但這對我來說仍然說不通。我認為機率應該是相等的。你拿到一張A牌,花色有什麼差別?
讓我們來看另一個更簡單的情況。假設女性 A說:「我有兩個孩子,至少有一個是男孩。」女性 B 說:「我有兩個孩子,大一點的叫約翰。」我們可以假設沒有一個叫約翰的女孩,也沒有女性會給多個孩子取同一個名字。使用條件機率,女性A的兩個孩子都是男孩的機率是pr(兩個男孩)/pr(至少一個男孩)= pr(兩個男孩)/(1-pr(兩個女孩))= (1/4)/(1-(1/4)) = (1/4)/(3/4) = 1/3。然而,女性B的較小孩子是男孩或兩個孩子都是男孩的機率是? ,因為說大孩子叫約翰並不能告訴我們任何關於較小孩子的資訊。
再舉一個例子,假設你去捷飛絡 (Jiffy Lube),他們以相同的價格提供兩個方案。方案 A 是他們會檢查四個零件,只更換第一個發現的瑕疵零件。方案 B 是他們只檢查一個問題,如果發現問題就會修復。你不想選擇方案 A 嗎?你的車進來時預計有相同數量的壞零件,但在方案 A 下發現問題的機率更大,因此在方案 A 下你離開時預計會有少量缺陷零件。同樣,測試任何 A 都可能出現唯一的 A,而測試黑桃 A 時不會檢查其他三種花色,因此它們更有可能是 A。
在四張牌撲克中,如何使用 5 張牌中的 4 張牌得出同花順的數量為 2072?
首先,我將同花順分為兩種:四張連續同花色的牌和五張連續同花色的牌。五張同花順的數量等於花色數 * 跨度數(A 到 10 為最低牌)= 4*10 = 40。對於四張同花順,有 11 種不同的跨度(A 到 J 為最低牌)。對於 A234 和 JQKA 同花順,第五張牌可以是 47 張牌中的一張(52 張牌減去已經取出的 4 張牌和可以組成五張同花順的第五張牌,這四張牌已經計算在內)。因此,跨距為 A234 或 JQKA 的同花順共有 4*2*47=376 張。其他九張牌,第五張牌有 46 種可能的牌(52 張牌減去已經取出的 4 張牌和可以組成五張同花順的兩張牌)。因此,跨距為 2345 到 TJQK 的同花順數量為 4*9*46=1656。因此,4張同花順的總數為40+376+1656=2072。
無論發出第17張牌是什麼,同花的機率都是100%。那麼,什麼時候發出第幾張牌,順子機率是100%呢?
只有45張牌才能保證順子。例如,即使你發了A、2、3、4、6、7、8、9、JQ和K,總共44張牌,你還是無法湊成順子。
尊敬的奇才先生,我對您的統計敏銳度讚歎不已。您能否幫我計算一下七張牌順子的機率?例如,七張牌梭哈中,A、2、3、4、5、6、7,或 2、3、4、5、6、7、8,或 7、8、9、10、J、Q、K。我們知道這不是真正的撲克牌型;然而,我們在玩牌時碰巧碰到了它,我們想知道它的機率是否比七張牌梭哈中普通葫蘆的機率更低。謝謝,您真是個博學之人。
你這麼奉承我,我怎麼能拒絕?首先,從 52 張牌中隨機抽出 7 張牌,不考慮順序,總共有(52,7) = 133,784,560 種組合方式。七張牌的順子有 8 種可能的組合範圍(最小的牌可能是 A 到 8)。如果牌型有 7 種不同的大小,那麼花色就有47 = 16384 種排列方式。注意,這包括所有相同花色的牌,這樣就能組成同花順。所以機率是 8*16,384/133,784,560 = 1/1020.6952。
如果我從一副牌中發出 4 張牌,其中至少有 1 張牌是黑桃的機率是多少?
零張黑桃的機率為 (39/52)*(38/51)*(37/50)*(36/49) = 0.303818。因此,至少出現一張黑桃的機率為 1-0.303818 = 0.696182。
在一副牌的遊戲中,四張牌中至少出現一張A和一張2的機率是多少?了解這一點對於奧馬哈遊戲來說很有用。
由機率101可知,Pr(A或B) = Pr(A) + Pr(B) - Pr(A和B)。因此,Pr(A和B) = Pr(A) + Pr(B) - Pr(A或B)。假設A拿到一張A,B拿到一張2。 Pr(A) = Pr(至少一張A) = 1-Pr(沒有A) = 1-combin(48,4)/ combin (52,4) = 1-0.7187 = 0.2813。沒有2的機率顯然相同。依照同樣的邏輯,pr(A或B) = Pr(至少一張A或2) = 1-Pr(沒有A也沒有2) = 1-combin(44,4)/combin(52,4) = 1 - 0.501435 = 0.498565。因此,至少得到一張 A 和一張 2 的機率是 0.2813 + 0.2813 - 0.498565 = 0.063962。
在六張牌的遊戲中連續 27 手拿到方塊 J 的機率是多少?
任一手拿到它的機率是 6/52。連續 27 手拿到它的機率是 (6/52) 27 = 20,989,713,842,161,800,000,000,000 分之一。
得到“死人之手”,即兩對 A 和 8 的機率是多少?
每對牌有六種組合方式,可以從四種花色中抽出兩種。單張牌有 44 張。因此,成功組合數為 6*6*44 = 1584。總共有 2,598,960 種組合方式,機率為 0.0609%。
我知道您已經回答過, 2005 年 4 月 3 日,拿到“死人之手”(兩對 A 和 8)的機率是 0.0609%,但我相信死人之手是“兩張黑 A、兩張黑 8 和一張梅花 Q”,那麼從一副標準中抽出這手牌的機率是多少?
只有一個方法可以拿到那一手牌。所以機率是 1/combin(52,5),也就是 2,598,960 分之一。
在一副標準的52張牌中,如果一張牌的花色相同,且不重複,那麼每種可能的五張牌型的機率是多少?例如,假設這手牌是A♠ A♣ A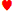 一個
一個 2. 在這手牌中,2 的花色不予考慮,可以代表牌堆中任四張 2。另一個例子是 AJ-8-6-5。在這手牌中,所有 5 張牌的花色都不予考慮,因此只有一種這樣的組合。另一個例子是:3♠ 3
2. 在這手牌中,2 的花色不予考慮,可以代表牌堆中任四張 2。另一個例子是 AJ-8-6-5。在這手牌中,所有 5 張牌的花色都不予考慮,因此只有一種這樣的組合。另一個例子是:3♠ 3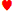 7♣ 7♠ Q。在這手牌中,兩張3和兩張4的花色不會被忽略,因為手中有不只一張3,但Q的花色是通用的。換句話說,任何牌中沒有重複的牌的花色都會被忽略,並且該手牌被視為可能的手牌之一,即使如果不忽略每張牌的花色,該手牌再次出現的可能性會有很多。因此,由五張特定牌組成的順子或同花,例如Q
7♣ 7♠ Q。在這手牌中,兩張3和兩張4的花色不會被忽略,因為手中有不只一張3,但Q的花色是通用的。換句話說,任何牌中沒有重複的牌的花色都會被忽略,並且該手牌被視為可能的手牌之一,即使如果不忽略每張牌的花色,該手牌再次出現的可能性會有很多。因此,由五張特定牌組成的順子或同花,例如Q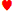 J♣ 10
J♣ 10 9
9 8♠ 或 A♠ J♠ 8♠ 7♠ 3♠ 只能出現一次,因為這些牌的任何其他組合,即使花色不同,也都屬於重複。因此,根據這個標準,任何一手牌的勝率是多少?換句話說,在一副標準的52張牌的牌組中,有多少種這樣的五張牌?感謝您的意見。
8♠ 或 A♠ J♠ 8♠ 7♠ 3♠ 只能出現一次,因為這些牌的任何其他組合,即使花色不同,也都屬於重複。因此,根據這個標準,任何一手牌的勝率是多少?換句話說,在一副標準的52張牌的牌組中,有多少種這樣的五張牌?感謝您的意見。
我對這個概念非常熟悉。五張牌共有134,459種不同的牌型。我之所以知道這一點,是因為我的第一個視訊撲克程式分析了所有2,598,960種可能的牌型,並花了好幾天才跑完一張賠率表。然而,如果只運行這134,459種牌型中的每一種,並根據該類別中所有牌型的數量進行加權,就可以將運行時間縮短95%。有時,如果遊戲的花色是特定的,例如我最近分析的“黑傑克紅利撲克” ,我就不得不重新啟用我的舊程序,用慢節奏的方式運行。
在玩五張牌梭哈時,如果使用 5 種花色而不是 4 種花色的牌,那麼獲勝的機率是多少?
五花撲克中的組合
| 手 | 組合 | 可能性 | 公式 |
| 五張相同的牌 | 十三 | 0.000002 | 十三 |
| 同花順 | 50 | 0.000006 | 5*10 |
| 四條 | 3900 | 0.000472 | 13*12*組合(5,4)*5 |
| 沖洗 | 6385 | 0.000773 | 5*(組合(13,5)-10) |
| 客滿 | 15600 | 0.001889 | 13*12*組合(5,3)*組合(5,2) |
| 直的 | 31200 | 0.003777 | 10*(5^5-5) |
| 三條 | 214500 | 0.025969 | 13*組合(12,2)*組合(5,3)*5^2 |
| 兩對 | 429000 | 0.051938 | 組合(13,2)*11*組合(5,2)^2*5 |
| 一對 | 3575000 | 0.432815 | 13*組合(12,3)*組合(5,3)*5^3 |
| 沒有什麼 | 3984240 | 0.48236 | (組合(13,5)-10)*(5^5-5) |
| 全部的 | 8259888 | 1 |
請注意,我顛倒了葫蘆和同花的順序。
一副標準撲克牌中,有多少種五張牌的組合是由兩種花色的牌組成的?
兩種花色可以分成 4 和 1 或 3 和 2。我們先來看看 4/1 分割的情況。對於有 4 張牌的牌,有 4 種花色可供選擇;對於有 1 張牌的牌,剩下 3 種花色可供選擇。從 13 種花色中選擇 4 種花色,共有 combin(13,4)=715 種方法。選擇一個花色則有 13 種方法。因此,兩種花色 4/1 分割的方式有 4×3×715×13=111,540 種。依照類似的邏輯,3/2 分割的方式有 4×3×combin(13,3)×combin(13,2)=267,696 種。因此,總機率為 (111540+267696)/combin(52,5) = 14.59%。
拿到2-3-4-5-7非同花的賠率是多少?非常感謝,這個網站太棒了!
謝謝。 (4 5 -4)/combin(52,5)= 1020/2598960 = 2,548 中的 1。
前幾天我在福克斯伍茲賭場觀看福克斯伍茲撲克經典賽的最後兩桌比賽。世界撲克巡迴賽主持人之一文斯·範·帕滕(Vince Van Patten)進來觀看比賽時,開始和一些在場的撲克高手進行各種賭注。他開價20比1,條件是參賽者能翻開一整副牌,牌面大小依次循環,並一邊翻開一邊大聲念出A、2、3、4等等直到K的牌,然後從A重新開始,且不翻出他們要宣布的牌。沒有人能翻完,文斯在大約10分鐘內贏了幾百美元,之後所有人都放棄了。我知道這肯定是可能的,但我懷疑文斯在開20比1的賠率時有點兒賣力。那麼,真正翻開整副牌的幾率有多大呢?
估算獲勝機率的簡單方法是假設每張牌都有12/13的機率不符合指定的點數。為了贏得這場賭注,受害者必須成功下注52次。 52次獲勝的機率是(12/13) /52=1.56% 。合理的賠率是63.2比1。在20比1的賠率下,文斯的優勢是67.3%(哎喲!)。
根據數學能力比我強的GM的說法,實際機率是1.6232727%。造成這種差異的原因是,每次選擇的結果都與先前的選擇呈正相關。
昨晚玩的時候,一位老玩家,一個狡猾、邋遢、好鬥的老玩家,在翻牌圈挑戰賭桌,想做等額的邊注。這位老頑固押注翻牌圈的三張牌中會有一張是A、2或J(有時他會把這三張可識別的牌換掉)。這個賭注的賠率是多少?非常感謝您的智慧。
在翻牌圈未出現任何牌型的情況下,任三個點數不出現在翻牌圈的機率為: combin (40,3)/combin(52,3) = 9880/22100 = 44.71%。所以這名玩家的優勢是 10.59%。
假設從一副52張牌的牌堆中發出五張牌,第一張是K。至少還有一張K的機率是多少?我看到你做過一道和這個類似的Ace題,但我不太明白。謝謝你的幫忙。
我比較喜歡用組合函數來回答機率問題。這樣一來,從一副牌中的48張非K牌中,選出四張非K牌的方法有(48,4) = 194,580種。從剩下的51張牌中,選出任四張牌的方法有(51,4) = 249,900種。因此,接下來四張牌中沒有K的機率是194,580/249,900 = 77.86%。因此,至少選出一種K的機率是100% - 77.86% = 22.14%。
有些人說,組合函數可能超出了問這類簡單機率問題的人的理解範圍。我並不反對這種說法,但創建這個網站的主要原因是想教我的讀者一些數學知識。組合函數在機率論中非常有用,可以節省大量時間。然而,即使沒有它,我們手頭上的問題也很容易回答。
第二張牌不是K的機率是48/51。這是因為牌堆裡還剩下48張非K牌,而牌堆裡總共剩下51張牌。如果第二張牌不是K,那麼第三張牌也不是K的機率就是47/50(47張非K牌除以剩餘的50張牌)。如此類推,其他四張牌都不是K的機率是(48/51)×(47/50)×(46/49)×(45/48) = 77.86%。其他四張牌都不是K的機率,換句話說,至少有一張K的機率是100% - 77.86% = 22.14%。
首先,從一副52張牌的牌堆中選出5張牌。然後,將它們的黑傑克點數(T、J、Q、K = 10,A = 1)相加。結果奇數/偶數的機率是多少?我認為,由於偶數牌數量過多,結果奇數的機率會更大。
令人驚訝的是,儘管52張牌中有30張是偶數,但奇數點數的機率卻高達50.03%。下表顯示了奇數/偶數點數的機率。
奇數/偶數問題
| 埃文斯 | 賠率 | 組合 | 可能性 | 和 |
| 0 | 5 | 15504 | 0.005965 | 奇怪的 |
| 1 | 4 | 155040 | 0.059655 | 甚至 |
| 2 | 3 | 565440 | 0.217564 | 奇怪的 |
| 3 | 2 | 942400 | 0.362607 | 甚至 |
| 4 | 1 | 719200 | 0.276726 | 奇怪的 |
| 5 | 0 | 201376 | 0.077483 | 甚至 |
| 全部的 | 2598960 | 1 |
如果從一副牌中抽出三張牌,其中剛好有一張是黑桃,那麼機率是多少?
第一張牌是黑桃,後兩張不是的機率是 (13/52)×(39/51)×(38/50) = 14.53%。你應該將這個機率乘以 3,因為黑桃可能是三張牌中的任何一張。所以答案是 3×14.53% = 43.59%。對於喜歡使用組合函數的人來說,答案是 13×combin(39,2)/ combin (52,3) = 9,633/22,100 = 43.59%。
選擇兩個介於 0 和 1 之間的隨機數(均勻分佈)。現在選擇其中較小的一個。選擇的平均值是多少? n 個數字的情況呢?
對於兩個數字,答案是 1/3;對於 n 個數字,答案是 1/(n+1)。我把答案發佈到我的數學題頁面,也就是第 194 題和第 195 題。
您正在玩一個包含三個人的遊戲:(a) 您自己,(b) 您的對手,以及 (c) 一名裁判。你們每人秘密選擇一個介於 0 到 1 之間的實數。所有數字都選好後,它們就會被揭曉。猜得最接近裁判數字且不超過的玩家獲勝。如果您猜得更接近,您將贏得 1 美元。如果您的對手猜得更接近,您將輸掉 1 美元。如果雙方都猜得超過或出現平局,則遊戲為平局。
如果對方隨機選擇,你能否選擇一個數字,使你的預期報酬最大化?如果對方也有策略呢?
希望你滿意,我花了一整天做第二部分,但答案還是錯的。為了避免讓讀者失去同樣的樂趣,我不會在這裡直接說出答案。我把這個問題分成了兩個問題,並在mathproblems.info上發布了答案和解答,分別是問題 196 和 197。
如果從標準的 52 張牌中隨機抽出五張牌,那麼四種花色都出現的機率是多少?
必須有一種花色包含兩張牌,還有三種花色,每張牌包含一張牌。出現兩次的花色有四種可能的花色。對於出現兩次的花色,有 (13,2)=78 種組合方式可以從 13 種花色中選擇 2 種。對於其他三種花色,每種花色都有 13 種可能的花色。因此,總組合數為 4 × 78 × 13 × 13 × 13 = 685,464。從 52 張牌中選出 5 張牌,有 (52,5)=2,598,960 種組合方式。因此,機率為 685,464/2,598,960 = 26.37%。
任兩個選定的牌型,例如皇后和國王,在一副隨機的牌中連續出現的機率是多少?有人跟我挑戰,要我跟他打個等額的賭,賭這件事會發生。
根據隨機模擬,機率是48.64%。所以,我會接受這個賭注。
您能否推薦一個函數,將 52 張牌中的任意五張牌映射到 0 到 2,598,959 之間的整數?
是的。首先給每張卡片分配一個從 0 到 51 的值。將卡片命名為 c1 到 c5,並依 c1 為最低、c5 為最高的順序排列。然後呼叫以下函數:
int GetIndex(int c1,int c2,int c3,int c4,int c5)
{
傳回組合(c5,5) + 組合(c4,4)+ 組合(c3,3) + 組合(c2,2) + 組合(c1,1);
}
其中,combin 傳回傳統值,但如果第一個值小於第二個值,則傳回 0,如下所示:
int 組合(int x,int y)
{
如果(y>x)
返回 0;
別的
{
int i,n;
n=1;
對於(i = x-y + 1;i <= x;i ++)
n*=i;
對於(i=2;i<=y;i++)
n/=i;
返回 n;
}
}
如果您這樣做是為了存取數組元素,請按如下方式載入數組。
計數=0;
對於(c5 = 4;c5 < 52;c5 ++)
{
對於(c4 = 3;c4 < c5;c4++)
{
對於(c3 = 2;c3 < c4;c3++)
{
對於(c2 = 1;c2 < c3;c2++)
{
對於(c1 = 0;c1 < c2;c1 ++)
{
index_array[count]=無論你想要什麼;
計數++;
}
}
}
}
}
從 10 張同花順中抽出 3 張,持有 3 張同花順且有 1 張缺口的機率是多少?

這是一個二項分佈問題。其一般公式是:如果某個事件的機率為 p,且每個結果都是獨立的,那麼事件在 t 次試驗中恰好發生 w 次的機率為(t,w)×p w ×(1-p) tw 。
在這種情況下,有兩種方法可以組成同花順。你需要一張方塊8和另一張方塊6或J。從牌堆剩下的47張牌中抽出2張,一共有combin(47,2)=1,081種方法。因此,任何一手牌中抽出同花順的機率是2/1,081 = 0.0018501。10張牌中抽出3張的機率是combin(10,3)×0.0018501 3 ×(1-0.0018501) 7 = 0.0001007501017531,07531,0750175,0075,0175017531753。
將兩副54張牌(包括兩張鬼牌)洗在一起。給一位玩家一半。這位玩家拿到全部四張紅色3的機率是多少?
有 4 張紅色 3 和 104 張其他牌。只有一個方法可以湊齊所有 4 張紅色 3。玩家有 (104,50)= 1.46691 × 10 28種組合方式可以湊齊另外 104 張牌中的 50 張。總組合數為 (108,54)= 2.48578 × 10 30 。組合數 (104,50)/組合數 (108,54) = 0.059012。
如果您不喜歡處理如此大的數字,這裡有一個替代解決方案。將四個紅色三號依 1 到 4 進行編號。第一個紅色三號在玩家牌堆中的機率是 54/108。現在移除前三個。玩家擁有第二個紅色三號的機率是 53/107,因為玩家剩餘 53 張牌,而牌堆裡還有 107 張。同樣,玩家擁有第三個紅色三號的機率是 52/106,第四個紅色三號的機率是 51/105。 (54/108) × (53/107) × (52/106) × (51/105) = 0.059012。
這個問題是在我的同伴網站Wizard of Vegas的論壇中提出並討論的。
您在2010年12月14日的專欄中寫道,賭場特別提到的「AAAAAKK」牌型在撲克歷史上可能從未出現過。據另一位荷官說,一位玩家在2010年11月在主街車站(Main Street Station)拿到了這手牌。
有意思。我之前寫過,我估計內華達州每23.7年就會出現一次這種手。我想那次就是其中一次。
假設你選擇兩個等級,例如國王和王后。在一副隨機洗好的52張牌中,國王和王后至少出現一次相鄰的機率是多少?
我的機率是48.6279%。如果你想下注的話,「是」的合理賠率是1.0564比1。
我聽說最近有一場「完美」的橋牌比賽,每位玩家都拿到了四張花色之一的13張牌。這樣的機率是多少?
也有傳言稱,2011 年在沃里克郡舉行的一場惠斯特牌局中也發生過類似的事情。為了方便其他讀者,我想問的是,將一副 52 張牌的撲克牌分成四組,每組 13 張,每組完全由某一花色的 13 張牌組成的機率是多少。
將 52 張牌分成四組,每組 13 張,一共有 combin(52,13)combin(39,13)*combin(26,13) = 53,644,737,765,488,800,000,000,000,000 種可能的方式。 4! = 24 是獲勝組合數,因為您可以按照自己希望的方式將四種花色分配給四位玩家。因此,獲勝幾率等於 2,235,197,406,895,370,000,000,000,000 分之一。為了更直觀地理解這個數字,假設地球上 75 億人以每秒一次的速度打橋牌,那麼在 50 億年後太陽爆炸之前,有人發出所謂完美牌型的機率是 16,558 分之一。
然而,有些人將「完美」牌型定義為一位玩家拿到任意花色的全部13張牌。我指出,這種情況發生的機率是39,688,347,497場遊戲中的1分之一。這種情況在地球上的某個地方可能偶爾會發生。
在德州撲克遊戲中,兩位玩家同時使用兩張底牌拿到同花的機率是多少?
首先,讓我們確定可能發生這種情況的玩家牌和公共牌的組合數。顯然有四種花色。那麼,從給定花色的 13 張牌中選出 4 張,一共有 combin(13,4)=715 種組合方式。
其次,一種可能發生這種情況的方式是,玩家在牌桌上有三張相同花色的牌,另外兩張在另外39張牌中。牌桌上有三張相同花色的牌,組合方式有(9,3)=84種。然後,有組合方式有(39,2)=741種,可以從另外三種花色的39張牌中再選出兩張。因此,牌桌上有三張相同花色的牌,組合方式有84*741=62,244種。
第三,另一種可能發生這種情況的方式是,玩家在公共牌上有四張相同花色的牌,另一張在另外 39 張牌中。公共牌上有選擇花色剩餘 9 張牌中的 4 張,共有 combin(9,4)=126 種方法。然後,有 39 種方法可以從其他三種花色的另外 39 張牌中再選一張。然而,並非所有這些方法都會導致兩位玩家都使用兩張底牌。要滿足該條件,公共牌上必須有該花色的最小牌。在 8 張該花色的牌中,出現這種情況的機率是 4/8 = 1/2。因此,公共牌上有四張該花色的牌共有 126*39*(1/2)=2,457 種方法。
第四,最後一種情況是,玩家手中持有五張相同花色的牌。共有 combin(9,5)=126 種組合方式,即牌桌上有五張相同花色的牌。然而,並非所有組合方式都會導致兩位玩家都使用兩張底牌。要滿足該條件,牌桌上必須有該花色的最小兩張牌。在目前牌桌上有九張相同花色的牌中,出現這種情況的機率為 combin(5,2)/combin(9,2) = 10/36 = 5/18。因此,共有 126*(5/18)=35 種組合方式,即牌桌上有四張相同花色的牌。
因此,發生這種情況的組合數為 715*(62,244 + 2,457 + 35) = 46,286,240。
從 52 張牌中挑選 4 張作為玩家底牌,然後從牌面上剩餘的 48 張牌中挑選 5 張作為玩家底牌,總組合數為 combin(52,4)*combin(48,5) = 463,563,500,400。
因此,機率為 46,286,240 / 463,563,500,400 = 0.000399395 = 2,504 分之一。
這個問題是在我的Wizard of Vegas論壇中提出並討論的。
一位賭場荷官正在研究一種新的三張牌撲克遊戲。她從一副標準牌中取出所有人頭牌,並徹底洗牌。然後,她給玩家1發了3張牌,給玩家2發了3張牌,給玩家3發了3張牌,最後給玩家4發了3張牌。四手牌都包含順子(任意花色的JQK)的機率是多少?
[劇透=解]
每次發牌給一位玩家。第一位玩家拿到每種等級的牌的機率為 4^3/combin(12,3) = 64/220。
假設第一個玩家拿到順子,那麼牌堆裡每個點數的牌就剩下三張了。第二位玩家拿到每個點數一張的機率是 3^3/combin(9,3) = 27/84。
假設前兩位玩家拿到順子,那麼牌堆裡每個點數的牌就剩下兩張了。那麼第三位玩家拿到每種點數各一張的機率是 2^3/combin(6,3) = 8/20。
假設前三名玩家拿到了順子,那麼牌堆裡就剩下一張牌,每張牌都剩下一張。這三張牌顯然組成了順子。
因此,四名玩家全部拿到順子的機率為 (64/220)*(27/84)*(8/20)*1 = 216/5775 = 72/1925 = 3.74%。
[/spoiler]這個問題是在我在 Wizard of Vegas 的論壇上提出並討論的,從這篇文章開始。
假設我有一副48張的牌,四種花色,每種花色12張。如果我抽15張牌,那麼我抽到每種花色至少一張牌的機率是多少?
讓我們從 100% 開始,減去導致少於四種花色的機率。
例如,48張牌中沒有紅桃的機率是多少?有36張牌不是紅桃。從36張牌中選出15張的方法數為combin(36,15) = 5,567,902,560。由全部48張牌中選出15張的方法數為1,093,260,079,344。因此,15張牌中沒有紅桃的機率為5,567,902,560 / 1,093,260,079,344 = 0.005093。
接下來,讓我們將其乘以四,得到缺少任何花色(而不僅僅是紅心)的機率:4 × combin(36,15)/combin(48,15) = 0.02037174。
然而,這會導致某些情況重複計算。假設拿到 15 張黑牌。這樣會忽略紅桃和方塊。這種情況就會重複計算。因此,我們需要進行修正。從四種花色中選擇兩種花色,共有 combin(4,2) = 6 種方法。所有 15 張牌都是任兩種特定花色的機率為 combin(24,15)/combin(48,15) = 1307504/1,093,260,079,344 = 0.00000120。如上所述,從四種花色中選擇兩種花色有六種方法,因此所有牌都是兩種花色的方法數為 6 × combin(24,15)/combin(48,15) = 0.00000718。
減去重複計算的結果,我們得到出現兩套或三套花色的機率為 0.02037174 - 0.00000718 = 0.02036456。
請注意,我們不需要擔心一種花色的代表,因為不可能從 12 張牌中選擇 15 張。
最後一步,從 100% 減去 2 或 3 種花色的機率,得到全部四種花色出現的機率:1.00000000 - 0.02037174 = 0.97963544。
我在Wizard of Vegas論壇上提出並討論了這個問題。
如果我從一副洗好的(假定是隨機的)牌中發出 13 張牌,我應該會看到多少種不同的等級?
如果存在的話,這就是馬可夫鏈類型的問題。
下表顯示了從 1 到 52 的所有牌張中,0 到 4 張牌的預期等級數。
根據發牌預測排名
| 牌 | 0 排名 | 1 級 | 2級 | 3個等級 | 4個等級 | 預期的 等級 |
|---|---|---|---|---|---|---|
| 1 | 12.000000 | 1.000000 | 0.000000 | 0.000000 | 0.000000 | 1.000000 |
| 2 | 11.058824 | 1.882353 | 0.058824 | 0.000000 | 0.000000 | 1.941176 |
| 3 | 10.174118 | 2.654118 | 0.169412 | 0.002353 | 0.000000 | 2.825882 |
| 4 | 9.343577 | 3.322161 | 0.324994 | 0.009220 | 0.000048 | 3.656423 |
| 5 | 8.564946 | 3.893157 | 0.519088 | 0.022569 | 0.000240 | 4.435054 |
| 6 | 7.836014 | 4.373589 | 0.745498 | 0.044178 | 0.000720 | 5.163986 |
| 7 | 7.154622 | 4.769748 | 0.998319 | 0.075630 | 0.001681 | 5.845378 |
| 8 | 6.518655 | 5.087731 | 1.271933 | 0.118319 | 0.003361 | 6.481345 |
| 9 | 5.926050 | 5.333445 | 1.561008 | 0.173445 | 0.006050 | 7.073950 |
| 10 | 5.374790 | 5.512605 | 1.860504 | 0.242017 | 0.010084 | 7.625210 |
| 11 | 4.862905 | 5.630732 | 2.165666 | 0.324850 | 0.015846 | 8.137095 |
| 12 | 4.388475 | 5.693157 | 2.472029 | 0.422569 | 0.023770 | 8.611525 |
| 十三 | 3.949628 | 5.705018 | 2.775414 | 0.535606 | 0.034334 | 9.050372 |
| 14 | 3.544538 | 5.671261 | 3.071933 | 0.664202 | 0.048067 | 9.455462 |
| 15 | 3.171429 | 5.596639 | 3.357983 | 0.808403 | 0.065546 | 9.828571 |
| 16 | 2.828571 | 5.485714 | 3.630252 | 0.968067 | 0.087395 | 10.171429 |
| 17 | 2.514286 | 5.342857 | 3.885714 | 1.142857 | 0.114286 | 10.485714 |
| 18 | 2.226939 | 5.172245 | 4.121633 | 1.332245 | 0.146939 | 10.773061 |
| 19 | 1.964946 | 4.977863 | 4.335558 | 1.535510 | 0.186122 | 11.035054 |
| 20 | 1.726771 | 4.763505 | 4.525330 | 1.751741 | 0.232653 | 11.273229 |
| 21 | 1.510924 | 4.532773 | 4.689076 | 1.979832 | 0.287395 | 11.489076 |
| 22 | 1.315966 | 4.289076 | 4.825210 | 2.218487 | 0.351261 | 11.684034 |
| 23 | 1.140504 | 4.035630 | 4.932437 | 2.466218 | 0.425210 | 11.859496 |
| 24 | 0.983193 | 3.775462 | 5.009748 | 2.721345 | 0.510252 | 12.016807 |
| 二十五 | 0.842737 | 3.511405 | 5.056423 | 2.981993 | 0.607443 | 12.157263 |
| 二十六 | 0.717887 | 3.246098 | 5.072029 | 3.246098 | 0.717887 | 12.282113 |
| 二十七 | 0.607443 | 2.981993 | 5.056423 | 3.511405 | 0.842737 | 12.392557 |
| 二十八 | 0.510252 | 2.721345 | 5.009748 | 3.775462 | 0.983193 | 12.489748 |
| 二十九 | 0.425210 | 2.466218 | 4.932437 | 4.035630 | 1.140504 | 12.574790 |
| 三十 | 0.351261 | 2.218487 | 4.825210 | 4.289076 | 1.315966 | 12.648739 |
| 31 | 0.287395 | 1.979832 | 4.689076 | 4.532773 | 1.510924 | 12.712605 |
| 三十二 | 0.232653 | 1.751741 | 4.525330 | 4.763505 | 1.726771 | 12.767347 |
| 33 | 0.186122 | 1.535510 | 4.335558 | 4.977863 | 1.964946 | 12.813878 |
| 三十四 | 0.146939 | 1.332245 | 4.121633 | 5.172245 | 2.226939 | 12.853061 |
| 三十五 | 0.114286 | 1.142857 | 3.885714 | 5.342857 | 2.514286 | 12.885714 |
| 三十六 | 0.087395 | 0.968067 | 3.630252 | 5.485714 | 2.828571 | 12.912605 |
| 三十七 | 0.065546 | 0.808403 | 3.357983 | 5.596639 | 3.171429 | 12.934454 |
| 三十八 | 0.048067 | 0.664202 | 3.071933 | 5.671261 | 3.544538 | 12.951933 |
| 三十九 | 0.034334 | 0.535606 | 2.775414 | 5.705018 | 3.949628 | 12.965666 |
| 40 | 0.023770 | 0.422569 | 2.472029 | 5.693157 | 4.388475 | 12.976230 |
| 41 | 0.015846 | 0.324850 | 2.165666 | 5.630732 | 4.862905 | 12.984154 |
| 四十二 | 0.010084 | 0.242017 | 1.860504 | 5.512605 | 5.374790 | 12.989916 |
| 43 | 0.006050 | 0.173445 | 1.561008 | 5.333445 | 5.926050 | 12.993950 |
| 四十四 | 0.003361 | 0.118319 | 1.271933 | 5.087731 | 6.518655 | 12.996639 |
| 45 | 0.001681 | 0.075630 | 0.998319 | 4.769748 | 7.154622 | 12.998319 |
| 46 | 0.000720 | 0.044178 | 0.745498 | 4.373589 | 7.836014 | 12.999280 |
| 四十七 | 0.000240 | 0.022569 | 0.519088 | 3.893157 | 8.564946 | 12.999760 |
| 四十八 | 0.000048 | 0.009220 | 0.324994 | 3.322161 | 9.343577 | 12.999952 |
| 49 | 0.000000 | 0.002353 | 0.169412 | 2.654118 | 10.174118 | 13.000000 |
| 50 | 0.000000 | 0.000000 | 0.058824 | 1.882353 | 11.058824 | 13.000000 |
| 51 | 0.000000 | 0.000000 | 0.000000 | 1.000000 | 12.000000 | 13.000000 |
| 52 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 13.000000 | 13.000000 |
我在Wizard of Vegas論壇上提出並討論了這個問題。
有人向我挑戰,要我進行以下賭注。我可以從一副標準撲克牌中選擇任意三個點數,寫下我的預測,但要保密到最後。例如,7-A-2。然後他提議和我打等額賭注,如果他猜對三次,他至少能猜出我的一個點數。我贏的幾率是多少?
要獲勝,對手的三次預測都必須全部錯誤。第一次預測有 10/13 的機率是錯誤的。第二次預測有 9/12 的機率是錯誤的,因為我們可以排除第一個猜測的排名的可能性。第三次預測有 8/11 的機率是錯誤的,因為我們可以排除前兩個猜測的排名的可能性。
這三件事必須同時發生,你才能獲勝。因此,你獲勝的機率是 (10/13) * (9/12) * (8/11) = 720/1716 = 41.96%。
在均等賭注下,從您的角度來看,這場賭注的莊家優勢是 16.08%(哎喲!)。
這個問題摘自歐文‧艾謝 (Owen E'Shea) 所著的《命題賭注之書》(第 7 期)。
有人跟我打賭,說他能在27次擲骰子中用兩顆骰子總共擲12點。如果他沒擲出,我就能贏12點。既然擲出12點的機率是1/36,那他平均需要擲36次才能擲出12點嗎?如果對手只擲27次,那看來我的勝算就大了。我猜對了嗎?還是我的計算有什麼問題?
兩次擲出 12 點的平均等待時間確實是 36 次,包括擲出 12 點本身。然而,這並不意味著它們恰好每 36 次擲出一次。擲不出 12 點的機率是 (35/36)。 27 次擲不出 12 點的機率是 (35/36)^27。因此,擲出至少一次 12 點的機率是 1-(35/36)^27 = 53.26%。
下表顯示了在20至36次投擲中至少擲出12的機率。注意,需要擲出25次才能在均等賠率下獲得優勢。
機率 12
| 麵包捲 | 可能性 |
|---|---|
| 20 | 43.07% |
| 21 | 44.66% |
| 22 | 46.19% |
| 23 | 47.69% |
| 24 | 49.14% |
| 二十五 | 50.55% |
| 二十六 | 51.93% |
| 二十七 | 53.26% |
| 二十八 | 54.56% |
| 二十九 | 55.82% |
| 三十 | 57.05% |
| 31 | 58.24% |
| 三十二 | 59.40% |
| 33 | 60.53% |
| 三十四 | 61.63% |
| 三十五 | 62.69% |
| 三十六 | 63.73% |
我們知道,在 52 張牌中,五張牌共有 combin(52,5)=2,598,960 種可能的組合。我的問題是,從五副牌的牌盒中可以得到多少種可能的五張牌?
讓我們一次討論一種類型的手。
- 五張相同的牌:一副牌中有 52 張不同的牌,有 52 種組合。
- 四張同點牌:四張同點牌有 52 種可能,單張同點牌有 51 種可能。因此,四條共有 52*51 = 2,652 種可能的組合。
- 三張相同的牌,兩張不同的牌:三張相同的牌有 52 種可能,一對有 51 種可能。因此,葫蘆有 52*51 = 2,652 種可能的組合。
- 三張相同的牌和兩張不同的單張牌:三張相同的牌有 52 種可能的組合,而兩張單張牌的組合有 (51,2)=1,275 種可能的組合。因此,三條有 52*1,275 = 66,300 種可能的組合。
- 兩對相同的牌和一張單張牌:兩張不同的牌組成對子,一共有 (52,2)=1,326 種組合。單張牌還有 50 種組合。因此,兩對牌共有 1,326*50=66,300 種可能的組合。
- 一對相同的牌和三張單張牌:該對牌共有 52 張可能的牌。那麼,從剩下的 51 張單張牌中選出 3 張,組合方式共有 (51,3)=20,825 種。因此,一對牌的組合數為 52*20,825 = 1,082,900。
- 五個單例:從 52 張牌中選出 5 張牌共有 combin(52,5)=2,598,960 種方法。
所有這些組合的總和是 3,819,816。
我在Wizard of Vegas論壇上提出並討論了這個問題。


