請問巫師 #415
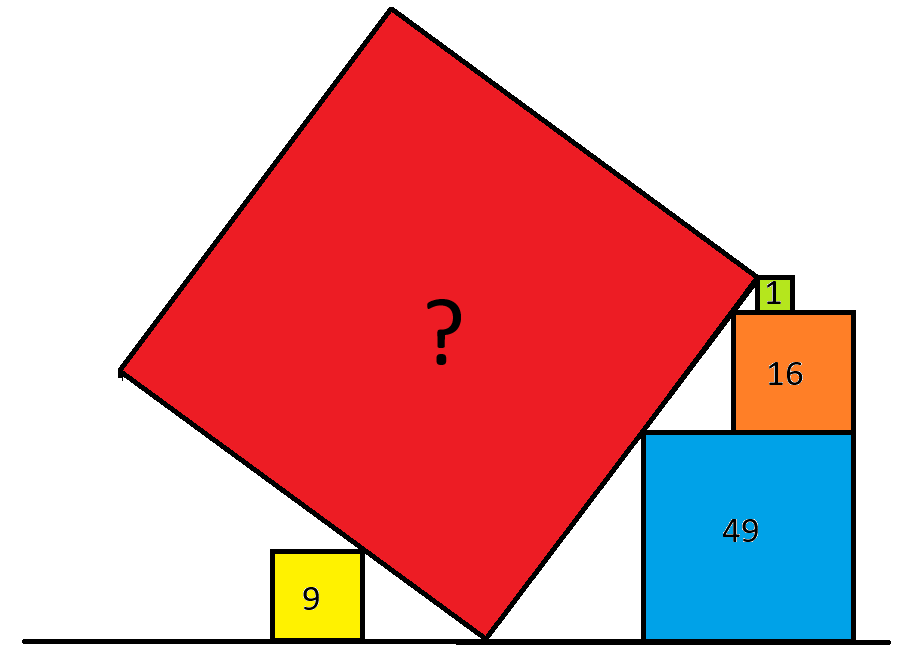
上圖中,數字代表四個正方形的面積。紅色正方形的面積是多少?
首先,黃色方塊對我們沒有任何幫助。它只是個轉移注意力的幌子,所以我們先忽略它。
接下來,考慮橘色正方形左側的三角形,如下圖所示。
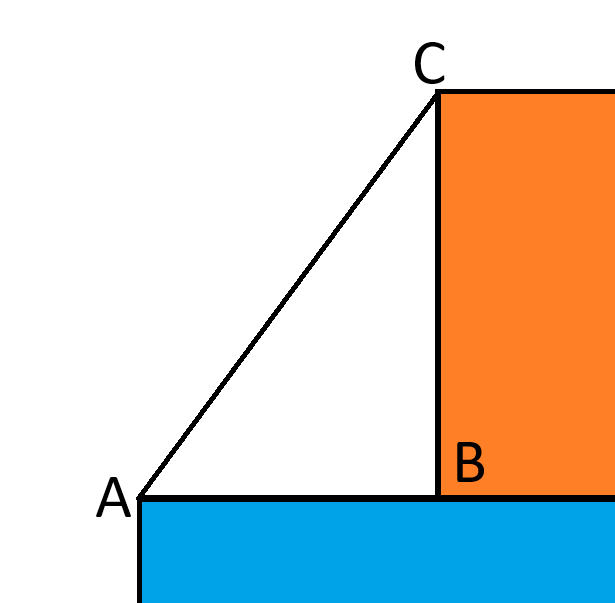
BC = sqrt(16) = 4。
AB = sqrt(49) - sqrt(16) = 7-4 = 3。
根據勾股定理,AC 2 = 4 2 + 3 2 = 25。
AC = sqrt(25) = 5。
右邊三個正方形的高度皆為 sqrt(49) + sqrt(16) + sqrt(1) = 12。
紅色正方形的邊長與右邊三個正方形的高度比將等於AC與BC之比=5/4。
所以,紅色正方形的邊長是(5/4)*12 = 15。
因此,紅色正方形的面積為15 2 = 225。
我在Wizard of Vegas論壇上提出並討論了類似的難題。
Mind Your Decisions YouTube 頻道也有類似的謎題。
面積等於週長的最小矩形是多少?
設矩形的尺寸為 x 和 y。
已知:xy = 2x + 2y。
2y-xy=2x
y(2-x) = 2x
y=2x/(2-x)
設 f(x) = 矩形面積 = x*y =
x*2x/(2-x) = 2x 2 /(2-x)
要找出最小面積,請使用商法則求導:
f'(x) = 4x(2-x) + 2x 2 / (2-x) 2 = 0
4x(2-x) + 2x 2 = 0
8x = 2x 2
x=4
若 x=4,y = 2*4/(4-2) = 8/2 = 4。
讓我們求解接近 4 的其他 x 值的 y。
若 x=3,y=6,面積為 18
若 x=5,則 y = 10/3,面積為 16+(2/3)。
很容易看出,在 x=4 和 y=4 的解最小。因此,最小可能的矩形是 4x4 = 16。
[/spoiler]在賭場抽獎中,彩券持有者旁的轉鼓中放有以下數量的彩券:
- 玩家 1 持有 6 張票。
- 玩家 2 持有 2 張票。
- 玩家 3 持有 1 張票。
- 其他 21 名玩家持有 21 張票。
賭場將抽取五張彩票,每張彩票對應五個相同的獎金。每位玩家只能中獎一次。如果抽到的彩券是由已經中獎的玩家抽取的,則該彩券將被丟棄,並重新抽取一張新的彩券。
玩家1、2和3同意根據各自在抽獎中的權益分配獎金。如何公平分配?
為了簡化這個問題,我假設如果彩券被已經中獎的玩家抽取,那麼獎金將會作廢。否則,計算起來會非常複雜,幾乎需要進行隨機模擬。
持有 n 張票的玩家沒有贏得獎品的機率是 combin(30-n,5)/combin(30,n)。
因此玩家 A 贏得獎品的機率為 1-combin(24,5)/combin(30,5) = 0.701739。
因此玩家 B 贏得獎品的機率為 1-combin(28,5)/combin(30,5) = 0.310345。
因此玩家 C 贏得獎品的機率為 1-combin(29,5)/combin(30,5) = 0.166667。
這些機率之和為1.178750。這就是該隊預期獲勝的場次。
在我看來,每個玩家應該獲得的份額等於他贏得獎品的機率除以該組預期的總獲勝數。
A 獲得 0.701739/1.178750 = 0.595324 股。
B 獲得 0.310345/1.178750 = 0.263283 股。
C 獲得 0.166667/1.178750 = 0.141393 份額。
我在Wizard of Vegas論壇上提出並討論了這個問題。


