請問巫師 #413
有沒有什麼方法可以進行滿足以下要求的秘密聖誕禮物交換:
- 沒有人會送禮物給自己。
- 沒有重來。
- 除了知道要為誰買東西之外,沒有人知道其他任何事情。
- 每場比賽都有同等的可能性。
是的!我把以下方法稱為 Hannah Fry 方法。
- 製作一組如下圖的卡片。每張卡片的頂部和底部都應有一個唯一的數字。在下面的例子中,數字是 23。
- 洗牌並重新堆疊。
- 保持卡片堆完好無損,沿著中間的線剪開每張卡片,形成兩疊。
- 切割並完成其中一個堆疊的切割。
- 將每堆卡片最上面的一張逐一分發給每位參與者。
- 建立編號清單並要求每個人在上面寫下他們的編號。
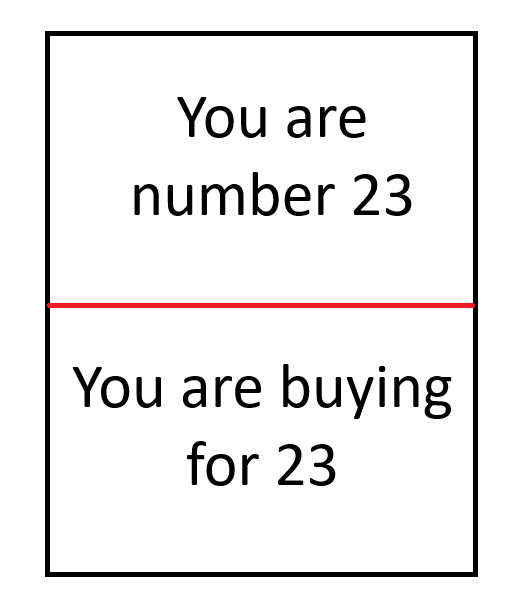
完成此程序後,每個人都會得到兩張卡片,例如,上面寫著“您是 13 號”和“您要為 7 號購買”。一旦清單填寫完畢,每個人都知道要為誰購買,但不知道誰會為他們購買。
一個游泳池裡充滿了鹽水。游泳池可容納1000立方公尺的水。一條花園軟管以每小時1立方公尺的速度將淡水注入游泳池。當淡水流入時,水以相同的速度從另一端流出。游泳池需要多久才能只剩下1%的鹽水?
答案是 2000 ln(10) =~ 4605.170186 小時 =~ 191.8821 天。
這是我的解決方案(PDF)。
平均而言,每個柏拉圖立體需要滾動多少次才能滾動到之前滾動過的任何一面?
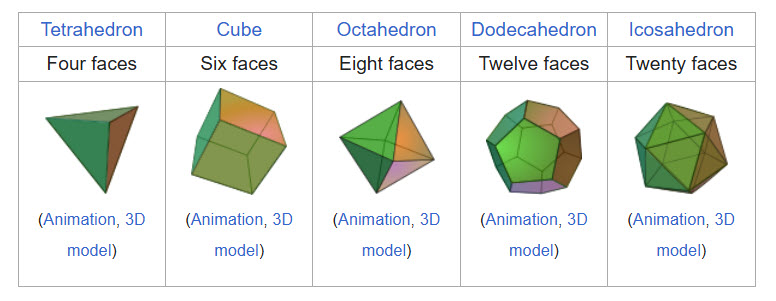
圖片來源:維基百科
這是以邊數計算的答案。
| 側面 | 平均卷數 |
|---|---|
| 4 | 3.218750 |
| 6 | 3.774691 |
| 8 | 3.846558 |
| 12 | 5.036074 |
| 20 | 6.293585 |
讓我們來計算一下六面立方體的情況。
- 實驗以兩次擲骰子結束的機率是 1/6。
- 實驗以三次擲骰子結束的機率是 (5/6)*(2/6)。
- 實驗以四次擲骰子結束的機率是 (5/6)*(4/6)*(3/6)。
- 實驗以五次擲骰子結束的機率是 (5/6)*(4/6)*(3/6)*(4/6)。
- 實驗以六次擲骰子結束的機率是 (5/6)*(4/6)*(3/6)*(2/6)*(5/6)。
- 實驗以七次投擲結束的機率是 (5/6)*(4/6)*(3/6)*(2/6)*(1/6)*(6/6)。
設 pr(n) = 實驗在 n 次滾動後結束的機率。
預期擲出的點數為:2*pr(2) + 3*pr(3) + 4*pr(4) + 5*pr(5) + 6*pr(6) + 7*pr(7) =
2*(1/6) + 3*(5/6)*(2/6) + 4*(5/6)*(4/6)*(3/6) + 5*(5/6)*(4/6)*(3/6)*(4/6) + 6*(5/6)*(4/6)*(3/6)*(4/6) + 6*(5/6)*(4/6)*(3/6) 7*(5/6)*(4/6)*(3/6)*(2/6)*(1/6)*(6/6) =~ 3.774691358。


