請問巫師 #412
在百家樂中,一副牌中一方(莊家或閒家)出現的次數至少是另一方的三倍的機率是多少?
如果我只是對此做一個估計,請原諒我。
平均每副牌有80.88手牌。平均7.70手牌為平局,莊家和閒家合計贏73.18手。如果一方的贏率是另一方的3倍,則需要出現54.89次,另一方需要出現18.30次。
在已結算的73.18個投注中,我們預計莊家贏37.09次,閒家贏36.09次。兩者的標準差均為4.28。要達到54.89次或更高的贏率,莊家贏4.16個標準差,閒家贏4.39個標準差。任何一方贏這麼多標準差的機率約為47,000分之一。
我在Wizard of Vegas論壇上提出並討論了這個問題。
以下是2028年總統大選得主的投注賠率。其他人獲勝的機率是多少?
| 賭注 | 支付 |
|---|---|
| 萬斯 | +250 |
| 紐瑟姆 | +750 |
| 夏皮羅 | +900 |
| 歐巴馬 | +1200 |
| 布蒂吉格 | +1400 |
| 惠特默 | +1600 |
| 拉馬斯瓦米 | +1600 |
| 德桑蒂斯 | +2000 |
像這樣的未來投注,賭場優勢通常約為 30%。如果我們假設在 -160 的賠率下注,那麼所有投注的賭場優勢將達到 29.95%。下表顯示了詳細資訊。 「隱含機率」表示投注完全公平時的機率。 「實際機率」是每個投注的公平機率除以所有公平機率總和。這表明其他人獲勝的機率為 43.1%。
| 賭注 | 支付 | 暗示 可能性 | 實際的 可能性 |
|---|---|---|---|
| 萬斯 | +250 | 0.285714 | 0.200136 |
| 紐瑟姆 | +750 | 0.117647 | 0.082409 |
| 夏皮羅 | +900 | 0.100000 | 0.070048 |
| 歐巴馬 | +1200 | 0.076923 | 0.053883 |
| 布蒂吉格 | +1400 | 0.066667 | 0.046698 |
| 惠特默 | +1600 | 0.058824 | 0.041204 |
| 拉馬斯瓦米 | +1600 | 0.058824 | 0.041204 |
| 德桑蒂斯 | +2000 | 0.047619 | 0.033356 |
| 場地 | -160 | 0.615385 | 0.431062 |
| 全部的 | 1.427602 | 1.000000 |
總回報率是隱含機率總和的倒數,即 1/1.427602 =~ 0.700475。回報率與莊家優勢總和為 1,因此莊家優勢為 1.000000 - 0.700475 = 0.299524。
我在Wizard of Vegas論壇上提出並討論了這個問題。
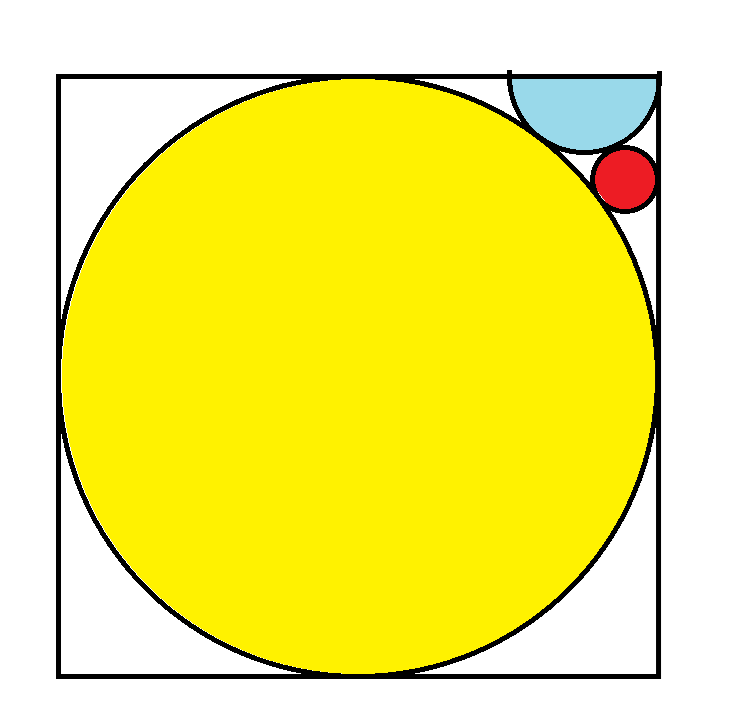
下圖中,黃色圓圈的半徑為1,紅色圓圈的面積是多少?