WOO logo

Wizard 巫師推薦

請問巫師 #411

我認為，即使賭場每場遊戲的莊家優勢為0%，他們仍然能賺錢。這是因為玩家的資金管理不善，而且玩家的資金相對於賭場來說有限。你同意嗎？

anonymous

不，我不同意。

資金管理被高估了。無論玩家如何玩輪盤賭這樣的運氣遊戲，賭場優勢都無法被削弱。

至於賭場可以輕易地拖住玩家直到其破產的說法，賭場有可能先破產。假設一位玩家擁有10,000美元的資金，與任何米高梅幻影賭場對戰。截至本文撰寫時，米高梅幻影的市值為11,168,000,000美元。為了便於論證，進一步假設該公司擁有其100%的股份。如果這位玩家一直玩到任何一方破產，那麼他贏得整個公司的機率是1/1,116,801。考慮到玩家數量龐大，最終總有一位玩家會獲勝。

我知道每個州都會根據其人口數量獲得一定數量的國會席位。但是，他們究竟是怎麼算出來的呢？肯定有計算方法。一個州的人口增加，而總人口保持不變，有可能失去一個席位嗎？

anonymous

簡而言之，每個州至少先擁有一個席位。之後，每個新增席位都會逐一分配給能夠從中獲得「最大利益」的州。

如何計算「最大利益」則變得更加複雜。具體如下：

  1. 將「乘數」計算為以下兩項的幾何平均值： (1) 新增席位後總席位的百分比；(2) 該州實際席位比實際多一個時總席位的百分比。用公式表示，如果 n 是目前席位數，則乘數為 1/sqrt(n*(n+1))。
  2. 將“優先值”計算為該州的乘數和人口的乘積。

對每個州都進行相同的計算。優先級最高的州將獲得下一個席位。

以內華達州為例。 2020 年人口為 3,104,614，該州已有 4 個席位。乘數為 1/sqrt(4*5) = 1/sqrt(20) = 0.223607。優先權值為 3,104,614 * 0.223607 = 694,213。

雖然你沒問，但如果國會增加第436個席位，那麼這個席位就歸紐約州了。下表按順序顯示了所有50個州的優先值。

狀態人口目前席位乘數優先權值
紐約20,201,249二十六0.037743 762,447
俄亥俄州11,799,448 15 0.064550 761,651
德州29,145,505三十八0.025976 757,090
佛羅裡達21,538,187二十八0.035093 755,842
亞利桑那7,151,502 9 0.105409 753,835
加州39,538,223 52 0.019048 753,143
維吉尼亞州8,631,393 11 0.087039 751,266
愛達荷州1,839,106 2 0.408248 750,812
密西根州10,077,331十三0.074125 746,981
紐澤西州9,288,994 12 0.080064 743,715
賓州13,002,700 17 0.057166 743,315
麻薩諸塞州7,029,917 9 0.105409 741,018
喬治亞州10,711,908 14 0.069007 739,192
華盛頓7,705,281 10 0.095346 734,670
伊利諾州12,812,508 17 0.057166 732,442
西維吉尼亞州1,793,716 2 0.408248 732,281
猶他州3,271,616 4 0.223607 731,556
田納西州6,910,840 9 0.105409 728,466
馬裡蘭州6,177,224 8 0.117851 727,993
密蘇裡州6,154,913 8 0.117851 725,363
俄克拉荷馬州3,959,353 5 0.182574 722,876
北卡羅來納州10,439,388 14 0.069007 720,386
路易斯安那州4,657,757 6 0.154303 718,708
印第安納州6,785,528 9 0.105409 715,257
愛荷華州3,190,369 4 0.223607 713,388
德拉瓦州989,948 1 0.707107 699,999
肯塔基州4,505,836 6 0.154303 695,266
威斯康辛州5,893,718 8 0.117851 694,581
內華達州3,104,614 4 0.223607 694,213
南卡羅來納州5,118,425 7 0.133631 683,978
科羅拉多州5,773,714 8 0.117851 680,439
阿肯色州3,011,524 4 0.223607 673,397
明尼蘇達州5,706,494 8 0.117851 672,517
阿拉巴馬州5,024,279 7 0.133631 671,398
密西西比州2,961,279 4 0.223607 662,162
康乃狄克州3,605,944 5 0.182574 658,352
堪薩斯州2,937,880 4 0.223607 656,930
俄勒岡州4,237,256 6 0.154303 653,823
南達科他州886,667 1 0.707107 626,968
新墨西哥州2,117,522 3 0.288675 611,276
夏威夷1,455,271 2 0.408248 594,112
內布拉斯加州1,961,504 3 0.288675 566,237
新罕布夏州1,377,529 2 0.408248 562,374
緬因州1,362,359 2 0.408248 556,181
北達科他州779,094 1 0.707107 550,903
阿拉斯加州733,391 1 0.707107 518,586
佛蒙特643,077 1 0.707107 454,724
羅德島1,097,379 2 0.408248 448,003
蒙大拿1,084,225 2 0.408248 442,633
懷俄明州576,851 1 0.707107 407,895
全部的330,759,736 435 0.002296 759,495

關於你的第二個問題，是的，這是有可能的。我琢磨了好一會兒才找到這種情況發生的情況。首先假設一個國家有以下六個州。總共15個席位，分配如下：

狀態人口目前席位乘數優先權值
錯亂900 3 0.288675 259.807621
拒絕800 3 0.288675 230.940108
布利斯700 3 0.288675 202.072594
沮喪600 2 0.408248 244.948974
地獄邊境500 2 0.408248 204.124145
焦慮400 2 0.408248 163.299316
全部的3,900 15

接下來假設進行了人口普查，人口發生了顯著變化，但總人口保持不變，為 3,900，而焦慮黨的人口從 400 增加到 401。該黨在 15 個州中僅獲得一個席位。

狀態人口目前席位乘數優先權值
錯亂1,885 7 0.133631 251.893721
拒絕405 2 0.408248 165.340558
布利斯404 2 0.408248 164.932309
沮喪403 2 0.408248 164.524061
地獄邊境402 1 0.707107 284.256926
焦慮401 1 0.707107 283.549819
全部的3,900 15

我想強調的是，我花了很長時間調整這些數字才找到這種情況。總的來說，我覺得這個方法相當公平。

兩個圓內接於一個高為 81 的長方形。有一條長度為 56 的線段延伸到兩個圓的邊緣，經過圓相交處，並與矩形的垂直邊緣平行。

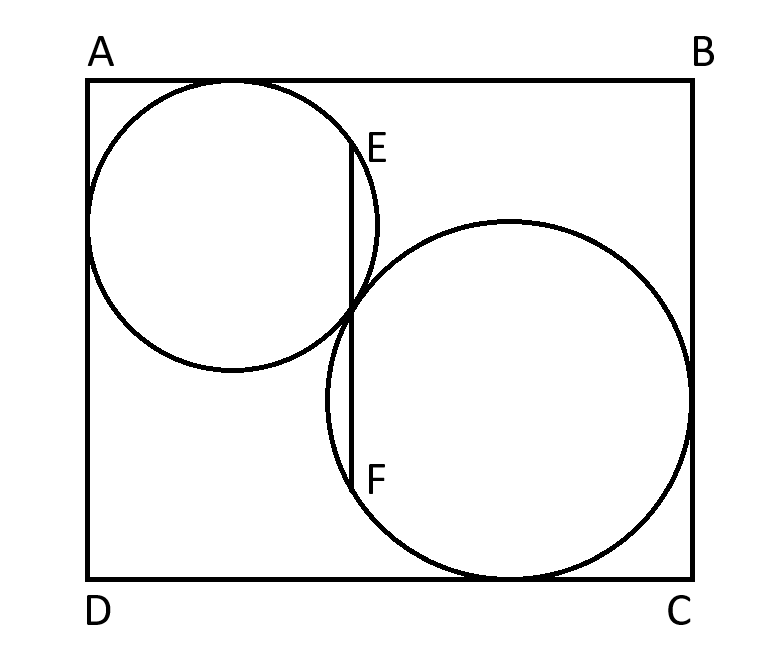
矩形的寬是多少？

anonymous

[劇透=答案]98[/劇透]

這是我的解決方案（PDF）。

我在Wizard of Vegas論壇上提出並討論了這個問題。