請問巫師 #399
如果你從第一張圖片中取出小正方形,並重新排列各個部分,總面積似乎仍然相同。這是怎麼回事?
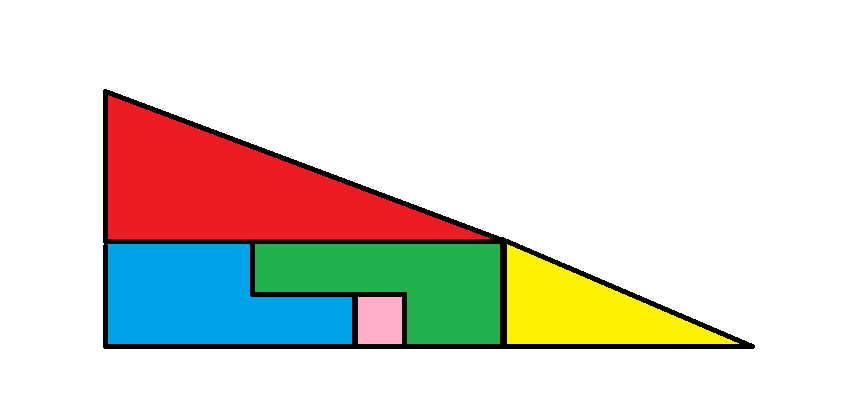
圖 1
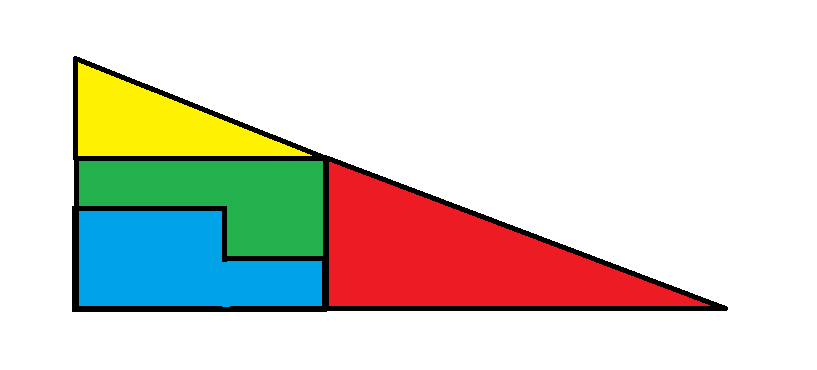
圖 2
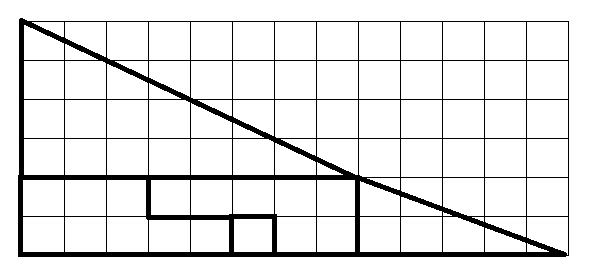
上圖顯示了網格上的第一個圖像,以便更好地查看每個部分的大小。
請注意,大紅色三角形的邊長分別為4和8。接下來請注意,較小的黃色三角形的邊長分別為2和5。換句話說,這兩個三角形都不成比例。兩個三角形的斜邊的斜率與圖中所示不同。一個斜率為0.5,另一個斜率為0.4。按照圖中所示的方式擺放這些碎片,看起來就像是一個邊長分別為5和13的大三角形,但實際上它並不是一個真正的三角形。
紅色三角形的面積為4*8/2=16。
黃色三角形的面積為2*5/2 = 5。
在第一幅圖中,另外三塊組成一個 2 x 8 的長方形,總面積為 16。
在第二幅圖中,另外兩塊組成一個 3 x 5 的長方形,總面積為 15。
第一張圖片的總面積是紅色三角形+黃色三角形+大矩形=16+5+16=37。
第二幅圖的總面積為紅色三角形+黃色三角形+小矩形=16+5+15=36。
總而言之,第一幅圖的正方形較小,但尺寸較大。這兩種情況下,所有碎片組合在一起形成一個大三角形,這是一種視覺錯覺。但事實並非如此。
一片大沙漠的邊緣有16輛摩托車。每輛摩托車一箱油可以行駛100英里。所有摩托車都是滿油狀態出發。摩托車之間可以換油。目標是讓一輛摩托車盡可能遠離出發點。它能跑多遠?
問題的關鍵是讓隊伍行駛一小段距離,然後把其中一輛摩托車剩餘的汽油加滿,再把其他摩托車的油箱加滿。
例如,一開始將一箱油分成16份,每輛摩托車一份。然後大家一起騎,直到油箱消耗了1/16,這樣全隊就能跑100/16=6.25英里。從一輛摩托車中取出15/16的油,再將1/16的油抽到其他15輛摩托車中,這樣就能剛好把油加滿。
然後重複同樣的過程,但剩下15輛摩托車,行駛1/15油箱所能行駛的距離,即100/15 = 6.666667英里。然後從一輛摩托車上取下另外14/15油箱的油,並將1/15油箱的油虹吸到另外14輛摩托車上。
繼續這個過程,最後一輛摩托車的總距離將為 (1/16) + (1/15) + (1/14) + ... + (1/1) =~ 338.072899 英里。
[/spoiler]這個問題是在我的Wizard of Vegas論壇中提出並討論的。
您對睡美人悖論有何看法?
為了其他讀者的利益,以下是睡美人問題/悖論中所提出的問題。
睡美人(SB)自願參加一項實驗。實驗的所有細節都如實向她解釋如下:
- 星期日:SB 被安樂死。她睡著後,將投擲一枚公平的硬幣。
- 星期一:SB 將於星期一被叫醒並被問到「硬幣正面朝上的機率是多少?」在她回答之後,她將被注射健忘症藥物,讓她再次陷入睡眠,忘記星期一發生的一切。
- 星期二:如果硬幣反面朝上,週一的事情就會再次發生。如果硬幣正面朝上,她就會睡一整天。
- 星期三:SB 再次被喚醒,什麼也沒問,實驗結束後就回家了。
問題是她應該如何回答週一甚至週二提出的問題?
我的回答
如果這個實驗重複一百萬次,我們預期會看到三種類型的覺醒,每種類型的發生機率相同:
- 硬幣落地正面,週一醒來。
- 硬幣落在反面,週一醒來。
- 硬幣落在反面,週二醒來。
這是因為週一醒來的次數應該在拋硬幣正面和反面時均等分配。此外,如果硬幣反面朝上,那麼週一和週二醒來的次數將完全相同。因此,在較大的樣本量下,三組醒來的次數大致相同。
在這些醒來的事件中,三分之一發生在拋硬幣正面之後。因此,硬幣正面朝上的機率是1/3。
1/2 陣營認為,SB 在每次醒來時都不會獲得任何額外信息,因此應該假設翻轉的每個結果都是同樣可能的。
為此,如果硬幣正面朝上,我會把這個問題擴展到999,999次喚醒。只有百萬分之一的喚醒發生在拋硬幣正面朝上之後。所以,很容易假設任何一次喚醒,都可能是拋硬幣反面朝上之後999,999次喚醒中的一次。換句話說,在這種情況下,正確答案是百萬分之一。
再擴展一下,如果讓SB預測每次醒來時拋硬幣的結果會怎麼樣?如果她猜對了,她將贏得1000美元。如果她預測“正面”,她可以預期贏得(1/2)*1000=500美元。如果她預測“反面”,她可以預期贏得(1/2)*2000=1000美元。所以,SB被喚醒本身就有利於硬幣拋向反面。
如果我的解釋不清楚,維基百科上的「睡美人問題」比我更深入地探討了這個問題,包括 SB 的其他可能的回應。
這個問題是在我的Wizard of Vegas論壇中提出並討論的。


