請問巫師 #395
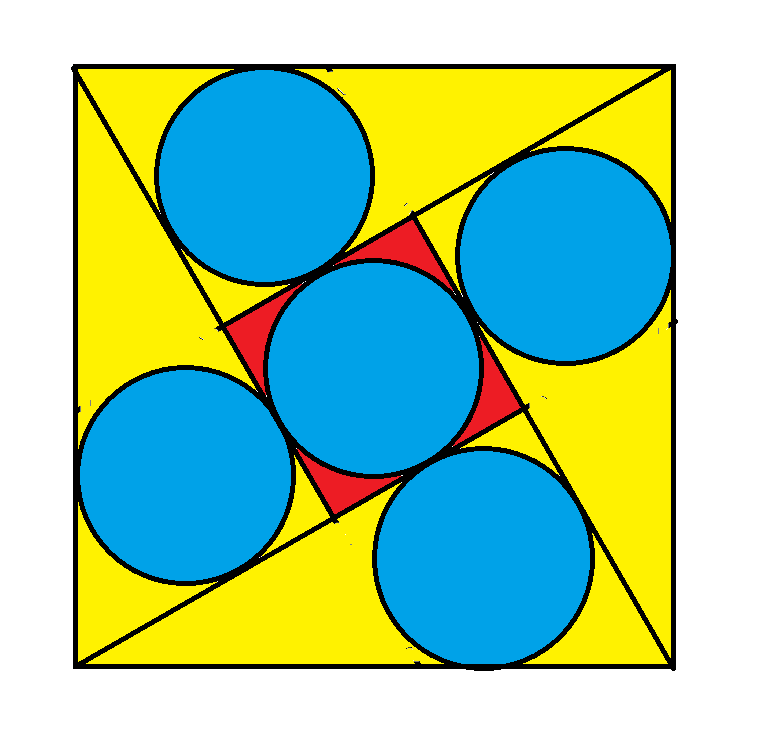
上圖由四個直角三角形和一個大正方形內嵌的小正方形組成。大正方形的邊長為1。五個圓的直徑相同。半徑是多少？
半徑 = (sqrt(3)-1)/4 =~ 0.183013。
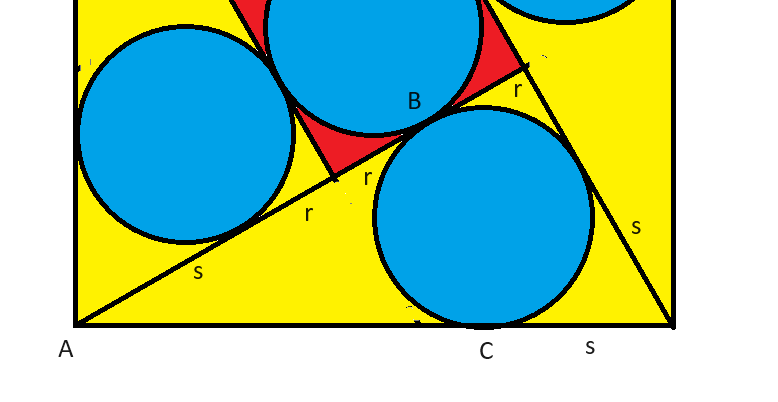讓我們考慮其中一個三角形。定義：- r = 圓的半徑
- s = 大正方形任一角與其內接三角形的切線最近的圓之間的距離。
觀察影像中的三角形，距離為：
- 短腿 = r+s
- 長腿 = 3r+s
- 斜邊 = 1
使用勾股定理公式：
(r+s) 2+ (3r+s) 2 =1
r² +2rs+ s² + 9r² +6rs+ s² =1
10r2 + 2s2 +8rs=1
我們需要另一個方程式來解決這個問題。我們先來看大正方形的邊長，已知它是1。 AB = AC。 AB = 2r+s，所以 AC = 2r+s。大正方形的剩餘邊長是s。所以：
2r + 2s = 1。
2秒=1-2r
s = 1/2 - r
讓我們將其代入畢達哥拉斯公式的方程式中：
10r 2 + 2(1/2 - r) 2 + 8r(1/2 - r) = 1
10r 2 + 2(1/4 - r + r 2 ) + 4r - 8r 2 = 1
2r 2 + 1/2 - 2r + 2r 2 + 4r = 1
4r 2 + 2r - 1/2 = 0
8r 2 + 4r - 1 = 0
使用二次方程式：
r = (-4 +/- 平方根(48))/16
r = (sqrt(3)-1)/4 =~ 0.183013。
這個問題來自Mind Your Decisions YouTube 頻道。 Presh 提供了一個不需要勾股定理的解。
[/spoiler]
我在Wizard of Vegas論壇上提出並討論了這個問題。
你對「正確與錯誤方式系統」有什麼看法？它的運作方式是，玩家下註一個單位的「不過關」。若擲出任何點數，玩家就在該點數上押註一個單位。如果擲出該點數，玩家就獲利；如果擲出七，玩家就不賠不賺。這看起來像是一場免費比賽。我是不是漏掉了什麼？
假設點數為4或10，玩家只需支付5%的贏利佣金。我們遵循拉斯維加斯的規則，如果come out擲出12，則在「不過線」投注中算「和局」（在內華達州北部，擲出2則算「和局」）。話雖如此，以下是所有可能的結果：
- 擲出 2 或 3：玩家因不透過賭注而贏得一個單位。
- 擲出 12 點：玩家繼續下注，不通過。
- 擲出 7 或 11：玩家因不透過賭注而輸掉。
- 點數為 4 或 10 且點數獲勝：玩家在買入賭注中贏得 1.95 個單位，在不通過賭注中輸掉 1 個單位，淨贏 0.95 個單位。
- 點數為 5 或 9 且點數獲勝：玩家在位置投注中贏得 1.4 個單位，在不過關投注中輸掉 1 個單位，淨贏 0.4 個單位。
- 點數為 6 或 8 且點數獲勝：玩家在位置投注中贏得 7/6 個單位，在不過關投注中輸掉一個單位，淨贏 1/6 個單位。
- 點數為 4 或 10 且點數輸：玩家在買注中輸掉 1 個單位，在不通過淨推中贏得 1 個單位。
- 點數為 5 或 9 且點數輸：玩家在位置投注中輸掉 1 個單位，在不及格投注中贏得 1 個單位，以進行淨推。
- 點數為 6 或 8 且點數輸：玩家在位置投注中輸掉 1 個單位，在不及格投注中贏得 1 個單位，以進行淨推。
下表總結了所有可能的結果。表格顯示了所有可能結果的機率、收益以及對回報的貢獻。右下角單元格顯示預期損失為 0.02951 個單位。
正確與錯誤的方法系統
| 事件 | 支付 | 可能性 | 返回 |
|---|---|---|---|
| 出來2或3 | 1 | 0.083333 | 0.083333 |
| 出來12 | 0 | 0.027778 | 0.000000 |
| 出場 7 或 11 | -1 | 0.222222 | -0.222222 |
| 4分獲勝 | 0.95 | 0.027778 | 0.026389 |
| 5分獲勝 | 0.4 | 0.044444 | 0.017778 |
| 6分獲勝 | 0.166667 | 0.063131 | 0.010522 |
| 8分獲勝 | 0.166667 | 0.063131 | 0.010522 |
| 9分獲勝 | 0.4 | 0.044444 | 0.017778 |
| 10分獲勝 | 0.95 | 0.027778 | 0.026389 |
| 4分損失 | 0 | 0.055556 | 0.000000 |
| 5分損失 | 0 | 0.066667 | 0.000000 |
| 6分損失 | 0 | 0.075758 | 0.000000 |
| 8分損失 | 0 | 0.075758 | 0.000000 |
| 9分損失 | 0 | 0.066667 | 0.000000 |
| 10分損失 | 0 | 0.055556 | 0.000000 |
| 全部的 | 1.000000 | -0.029512 |
此策略預期值為負的原因在於come out roll的擲出結果。擲出2或3時，有3種獲勝方式，擲出7或11時，有8種輸掉方式。誠然，如果玩家在come out roll中倖存下來，他就能獲得正的贏利，但這不足以彌補come out roll的預期損失。
我妻子有20%的時間是生氣的。當被問到「你生氣了嗎？」時，她90%的時間會在生氣時回答「不」。當被問到同樣的問題時，她95%的時間會回答「不」。我的問題是，根據這個問題的答案，她生氣的機率是多少？
這是一個經典的貝葉斯機率問題。
如果她回答“不”，那麼她生氣的機率就是 9/47 = 19.15%。
如果她回答“是”，那麼她瘋了的機率就是 1/3 = 33.33%。
對於以「如果 A 則 B」表示的問題，答案的公式是機率（A 和 B）/機率（B）。
如果答案是“否”，那麼她生氣的機率是 (0.2*0.9)/(0.2*0.9 + 0.8*0.95) = 0.18/0.94 = 9/47。
如果回答“是”，那麼她生氣的機率是 (0.2*0.1)/(0.2*0.1 + 0.8*0.05) = 0.02/0.06 = 1/3。
[/spoiler]