請問巫師 #391
1 2 + 2 2 + 3 2 + ... + n 2 = ?
[spoiler=答案]1 2 + 2 2 + 3 2 + ... + n 2 = n(n+1)(2n+1)/6 [/劇透]
這是我的解決方案。 (PDF)
假設你拋一枚公平硬幣一百萬次。只使用一個帶有五種基本算術函數(+、0、*、/、^)的簡單計算器,拋出正面和反面次數完全相同的機率是多少?一個近似的估計就夠了。
回想一下標準常態曲線的方程式:
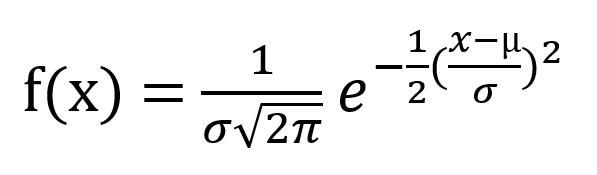
一次拋擲中反面朝上的期望次數為 0.5,反面朝上的期望平方次數也為 0.5。因此,一次拋擲中反面朝上的次數的變異數為 0.5 - (0.5) 2 = 0.5 - 0.25 = 0.25。一百萬次拋擲的變異數為 1,000,000 * 0.25 = 250,000。一百萬次拋擲的標準差是此變異數的平方根:sqrt(250,000) = 5,000。
設 x = 預期數量 500,000 的反面數。 x 的平均值為零。如圖所示,x 的標準差為 5,000。
因此 x=0 的機率為:
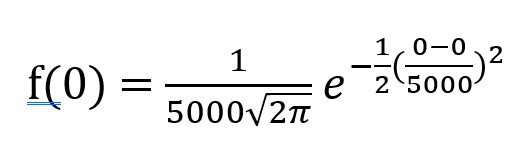
這簡化為 1/(5000*sqrt(2*π)) =~ 0.000797885 =~ 1 in 1253.314137。
[/spoiler]連結
維基百科關於標準常態曲線的條目。
你正以 15 英里/小時的速度沿著一條健身路徑騎自行車。路徑上有一些慢跑者,速度為 5 英里/小時。每個方向的慢跑者數量相等。你遇到的慢跑者中,有多少比例會與你反方向行駛?
假設該路徑長 15 英哩。
騎自行車的人會在我開始前 3 小時到開始後 1 小時的任何時間遇到從另一側開始的慢跑者,總共遇到 4 小時的慢跑者。
沿著同一方向,騎自行車的人會遇到比我早 2 小時或同時出發的慢跑者,總共 2 小時。
因此,反方向慢跑的人數將是反方向慢跑人數的兩倍。反方向慢跑的人數與所有慢跑人數的比例為4/(2+4) = 2/3。
相對於同方向的慢跑者,您的速度為 15-5 = 10 英里/小時。
相對於反方向的慢跑者,您的速度為 15+5 = 20 英里/小時。
因此,你遇到的反方向慢跑者數量是你的兩倍。因此,比例為 2/(1+2) = 2/3。
[/spoiler]我在Wizard of Vegas論壇上提出並討論了這個問題。


