請問巫師 #383
愛麗絲和比爾花了 3 個小時粉刷一棟房子。
愛麗絲和辛蒂花了 4 個小時粉刷一棟房子。
比爾和辛蒂花了 5 個小時粉刷一棟房子。
如果全部都畫的話需要多久?
[spoiler=答案]120/47 =~ 2.553191 小時[/劇透]
這是我的解決方案(PDF)。
一條橡皮筋拉長在兩個相鄰的直徑分別為 2 和 5 的圓上。拉長的橡皮筋的長度是多少?
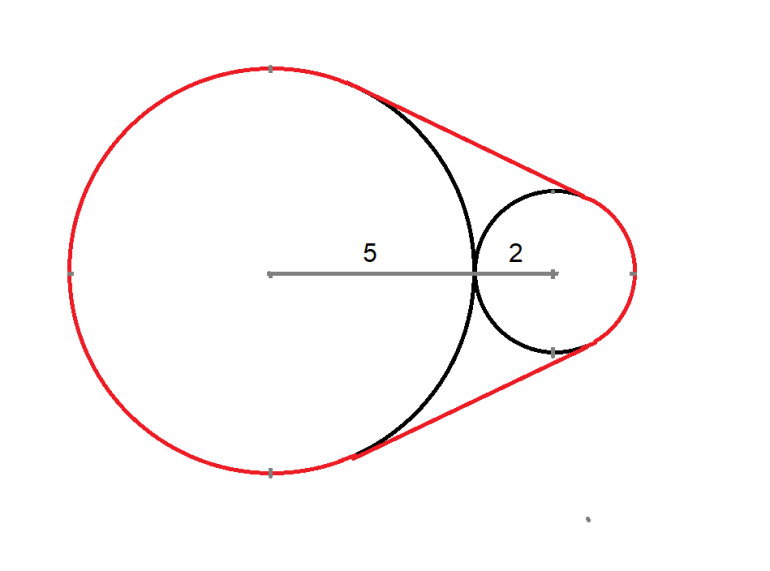
[spoiler=答案] 2*sqrt(40) + 10*(π - cos -1 (3/7)) =~ 37.297725 [/劇透]
這是我的解決方案(PDF)。
我在Wizard of Vegas論壇上提出並討論了這個問題。
考慮一下石頭剪刀布的遊戲,其中:
- 如果石頭戰勝剪刀,剪刀支付石頭 1 美元
- 如果剪刀勝過布,布付剪刀 2 美元
- 如果紙牌擊敗石頭,石頭支付紙牌 3 美元
- 領帶不涉及金錢交易
假設兩個邏輯學家正在玩遊戲。每個人的最優策略是什麼?
- 以 1/6 的機率出紙牌
- 以 1/3 的機率玩搖滾樂
- 出剪刀的機率為 1/2
讓我們為尋求最大化其收益的邏輯學家定義一些機率:
- r = 出石頭的機率
- p = 出紙牌的機率
- s = 出剪刀的機率
顯然r+p+s = 1。給定r和p,s = 1-rp。
如果兩個邏輯學家進行遊戲,那麼他們都會對對手的遊戲方式漠不關心,假設他們隨機選擇。
對手玩石頭的預期勝利是:3p-(1-rp) = 4p+r-1
對手玩紙牌的預期勝利是:2(1-rp) - 3r = 2-5r-2p
對手出剪刀的預期勝利是:r - 2p
這三個等式應該都是相等的。
將第一個和第三個設為相等,我們得到:
4p+r-1 = r - 2p
p = 1/6
將第一個和第二個設為相等,我們得到:
2 -5r - 2p = 4p + r -1
我們已經知道 p=1/6,這很容易讓我們得到 r=1/3。
s=1-rp = 1-(1/3)-(1/6) = 1/2。
因此,兩人都應該以 1/6 的機率出布,以 1/3 的機率出石頭,以 1/2 的機率出剪刀。
這個謎題的一般情況是,如果玩另外兩個符號,則根據有多少錢易手的權重來玩每個選項。
[/spoiler]我在Wizard of Vegas論壇上提出並討論了這個問題。


