請問巫師 #371
我看到阿拉斯加州現在採用排序選擇制進行國會選舉。假設2022年眾議院單一席次選舉中有22名候選人,總票數為20萬張,那麼最終獲勝者至少能獲得多少張第一選擇票?
對於那些不熟悉排序選擇選舉如何運作的人來說:
- 要求選民將他們的選擇從第一到最後進行排序。
- 如果任何候選人獲得多數票,那麼他就會獲勝。
- 否則,排名最後的候選人將被淘汰。在所有投票中,所有在優先順序上落後於該落選候選人的候選人都將上升一位。
- 重新計票。
- 回到步驟 2,直到有人獲得多數票。
*:請原諒我用了「他」。我的意思確實是“他或她”,但每次必須用代名詞的時候,我都討厭這樣寫。我還認為用“他們”語法不正確,因為“他們”應該是複數代名詞。
例如,假設某地有11名選民和4名候選人。這11名選民對其候選人的排名如下:
| 選擇 1 | 選擇 2 | 選擇 3 | 選擇 4 |
| B | 一個 | C | D |
| C | B | 一個 | D |
| C | 一個 | D | B |
| D | 一個 | C | B |
| 一個 | D | B | C |
| B | 一個 | D | C |
| B | D | 一個 | C |
| B | D | C | 一個 |
| C | D | B | 一個 |
| 一個 | D | B | C |
| 一個 | B | D | C |
以下為第一輪投票第一名得票狀況:
| 候選人 | 排名第 1 的投票 |
| 一個 | 3 |
| B | 4 |
| C | 3 |
| D | 1 |
由於無人獲得第一名的多數票,落選的候選人D被淘汰。他的選票基本上被抹去了,排名在他之後的候選人的排名都上升一位,具體如下:
| 選擇 1 | 選擇 2 | 選擇 3 |
| B | 一個 | C |
| C | B | 一個 |
| C | 一個 | B |
| 一個 | C | B |
| 一個 | B | C |
| B | 一個 | C |
| B | 一個 | C |
| B | C | 一個 |
| C | B | 一個 |
| 一個 | B | C |
| 一個 | B | C |
以下是第二輪投票第一名得票狀況:
| 候選人 | 排名第 1 的投票 |
| 一個 | 4 |
| B | 4 |
| C | 3 |
第二輪無人贏得多數第一名選票,因此落敗的候選人C被淘汰。他被淘汰後,第三輪的選票情況如下:
| 選擇 1 | 選擇 2 |
| B | 一個 |
| B | 一個 |
| 一個 | B |
| 一個 | B |
| 一個 | B |
| B | 一個 |
| B | 一個 |
| B | 一個 |
| B | 一個 |
| 一個 | B |
| 一個 | B |
以下是第二輪投票第一名得票狀況:
| 候選人 | 排名第 1 的投票 |
| 一個 | 5 |
| B | 6 |
B因此在第三輪投票中以六票的優勢贏得選舉。
回答你的問題,22位候選人總共獲得20萬張選票,一位候選人最多只能以兩票的優勢獲得第一名。這種情況有多種可能。例如,以下是第一名的得票總數:
| 候選人 | 總第一名 |
| 一個 | 85,311 |
| B | 57,344 |
| C | 28,672 |
| D | 14,336 |
| 埃 | 7,168 |
| F | 3,584 |
| 格 | 1,792 |
| 哈 | 896 |
| 我 | 448 |
| J | 224 |
| 鉀 | 112 |
| 左 | 56 |
| 米 | 二十八 |
| 否 | 14 |
| 哦 | 7 |
| 磷 | 2 |
| 問 | 1 |
| R | 1 |
| 秒 | 1 |
| T | 1 |
| ü | 1 |
| 五 | 1 |
| 全部的 | 20萬 |
如果除了兩位第一票的P之外的所有人都把候選人P當作第二選擇,那麼候選人P就會獲勝。
事實上,P 不必一直排在第二位。 P 只需在 Q、R、S、T、U 和 V 獲得第一名的六票中排在第二位即可。之後,即使先前被淘汰的候選人在排序選擇中領先 P,也不會對 P 造成不利影響。
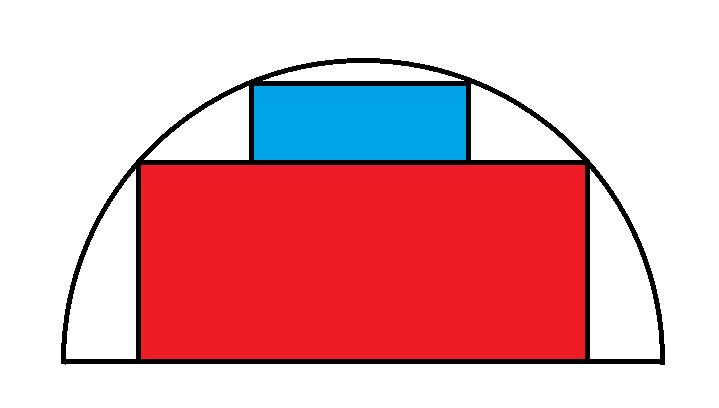
考慮一個半徑為 1 的半圓,裡面有兩個堆疊的長方形。這兩個矩形的最大合併面積是多少?
獨角獸有翅膀嗎?
不。
長角、有翅膀的馬被稱為角馬(cerapter)、飛馬(pegacorn)、天角馬(alicorn)或獨角馬(unisus)。雖然你沒問,但長著翅膀卻沒有角的馬(我只知道一例)被稱為飛馬(Pegasus)。獨角獸有角,但沒有翅膀。
請忽略同卵雙胞胎,假設每個孩子出生時男孩或女孩的機率均為50%。如果從2到5人的家庭中隨機抽出孩子,那麼男孩或女孩有姊妹的機率是多少?
有趣的是,無論家庭規模如何,無論性別如何,機率都是相同的。
以三口之家為例。以下是八種可能的男孩和女孩的排列順序:
血腦屏障
BBG
英國國立衛生研究院
布格
GBB
GBG
黃金海岸
GG
如果你從上面的清單中隨機挑選一個女孩,你會發現12個女孩中有9個有姊妹。 12個男孩也是如此,9個有姊妹。所以,機率是9/12 = 3/4。
當孩子數量為 n 時,任何孩子有姊妹的機率的一般公式是 1-(1/2) n-1 。
以下是家庭中孩子總數中有一個姊妹的機率:
- 1:0
- 2:1/2
- 3:3/4
- 4:7/8
- 5:15/16
- 6:31/32
或者說,男孩和女孩的機率相同也是合理的。兄弟姊妹的性別與你的性別無關。因此,只有家庭規模才重要,而不是自己的性別。
我在Wizard of Vegas論壇上提出並討論了這個問題。


