請問巫師 #367
我喜歡在擲骰子遊戲中押注所有數字。在擲出7之前,我預計會擊中多少個不同的數字?
為了其他讀者的利益,問題是詢問在擲出總數七之前,兩次擲骰子會擲出以下多少個總數:4、5、6、8、9 和 10。
答案是 2.375758。下表顯示了在指定範圍內擲出 0 到 6 個不同點數的機率。右下角單元格顯示的是擲出 7 點之前的平均不同點數。
滾動的唯一數字
| 全部的 | 可能性 | 預期的 |
|---|---|---|
| 6 | 0.062168 | 0.373009 |
| 5 | 0.101016 | 0.505079 |
| 4 | 0.129245 | 0.516979 |
| 3 | 0.151531 | 0.454594 |
| 2 | 0.170057 | 0.340114 |
| 1 | 0.185983 | 0.185983 |
| 0 | 0.200000 | 0.000000 |
| 全部的 | 1.000000 | 2.375758 |
拋一枚公平的硬幣,最終落在最初朝上的一面的可能性更大,這是真的嗎?
證據表明這是真的!
史丹佛大學的佩爾西·迪亞科尼斯和蘇珊·霍姆斯記錄了10000次拋硬幣實驗。硬幣落地時正面朝上的機率為50.8%(資料來源:美國數學學會期刊《數學科學動態》中的 「51%解決方案」)。出現如此高或更高比例的機率為5.48%。
為了從數學上證明這一點,我假設硬幣的實際旋轉次數服從泊松分佈。更具體地說,如果平均旋轉次數為m,那麼恰好旋轉n次的機率為exp(-m)*m^n/n!。為了說明泊松分佈,下圖顯示了假設平均值為10,硬幣旋轉0到25次的機率。
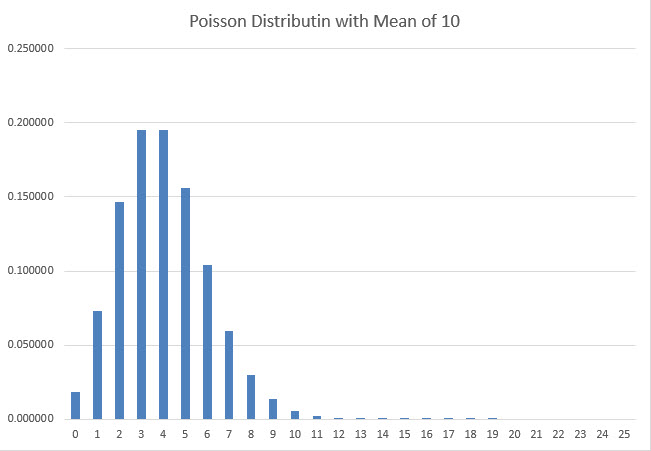
我選擇泊松假設的原因是,當平均值足夠大時,它遵循近似鐘形曲線的形狀,並且實際結果永遠不會低於零。
然後,我計算了不同半轉均值下,半轉次數為偶數(最終落地時與起始位置同一側朝上)的機率。下表顯示了平均值在0.5到5.0之間的結果。
旋轉次數為偶數和奇數的機率
| 平均革命 | 偶數總計 | 奇數總數 |
|---|---|---|
| 0.5 | 0.567667642 | 0.432332358 |
| 1 | 0.509157819 | 0.490842181 |
| 1.5 | 0.501239376 | 0.498760624 |
| 2 | 0.500167731 | 0.499832269 |
| 2.5 | 0.500022700 | 0.499977300 |
| 3 | 0.500003072 | 0.499996928 |
| 3.5 | 0.500000416 | 0.499999584 |
| 4 | 0.500000056 | 0.499999944 |
| 4.5 | 0.500000008 | 0.499999992 |
| 5 | 0.500000001 | 0.499999999 |
我開始好奇,為什麼偶數的機率總是大於 50%。事實證明,給定平均值 m,偶數的機率可以表示為 0.5 + e^(-2m)/2。 e 的任次方必定為正數,因此旋轉次數為偶數的機率也為正數。
您可以在此處看到我對該公式的證明。
您對“價格猜猜猜”節目中的拼字遊戲有何分析?
為了其他讀者的利益,讓我先介紹一下規則。
- 有一塊板,上面有 30 張卡片,編號為 1 到 30。
- 每張卡片的背面都有一個字母或單字「car」。每個字母或單字的分佈如下:
- C:11
- 答:11
- 評分:6
- 車:2
- 主持人讓玩家選擇兩張牌。
- 在定價遊戲之後(我不會深入討論),玩家有機會獲得最多三張卡片。
- 卡片將被翻轉。
- 玩家可以透過以下兩種方式贏得汽車:
- 玩家獲得每個字母的至少一張卡片(從而拼出單字 CAR)。
- 玩家獲得至少一張“CAR”卡。
- 在遊戲的任何時候,玩家都可以投降,並為每張未翻開的牌獲得 1,000 美元。
這是正在進行的比賽的片段。
下表顯示了獲勝的機率,根據玩家擁有的牌數計算,假設尚未翻開任何牌。
拼字比賽-獲勝機率
| 牌 | 可能性 獲勝 |
|---|---|
| 2 | 0.131034 |
| 3 | 0.371921 |
| 4 | 0.584018 |
| 5 | 0.734888 |
在翻開任何牌之前,玩家不應該放棄,因為假設汽車的價值合理。例如,即使只有兩張牌,玩家也有13.1%的機率至少拿到一張「CAR」牌。如果汽車的價值為15,263.16美元,那麼玩家應該對2,000美元的放棄價值無所謂。任何新車的價值都會高於這個數字。
以下是根據玩家未翻開的牌的數量對汽車價值的漠視點數。
拼字比賽-獲勝機率
| 牌 | 漠不關心 觀點 |
|---|---|
| 2 | 15,263.16 美元 |
| 3 | 8,066.23 美元 |
| 4 | 6,849.11 美元 |
| 5 | 6,803.75 美元 |


