請問巫師 #355
在電影《殺人執照》中,詹姆士龐德玩了三輪二十一點,每次玩五手。我注意到他一次都沒中過牌。這幾率是多少?
您可以在YouTube上找到該場景的片段。
遊戲中確實出現了大量可疑的大牌,不是嗎?以下是我能辨認出的牌。請注意,在某些情況下,牌可能看不清楚。
殺人執照-觀察等級
| 秩 | 觀察到 |
|---|---|
| 2 | 0 |
| 3 | 0 |
| 4 | 0 |
| 5 | 2 |
| 6 | 2 |
| 7 | 1 |
| 8 | 4 |
| 9 | 4 |
| 10 | 8 |
| J | 3 |
| 問 | 6 |
| 鉀 | 4 |
| 一個 | 1 |
| 全部的 | 三十五 |
你說得對,邦德最初的15手牌一手都沒要到。他分了一次8,但分完之後也沒要到。以下是他最初15手牌的行動統計:
- 雙倍 — 1
- 分裂 — 1
- 站立 — 13
以下是每個初始行動的基本策略機率,假設有六副牌,允許分牌後加倍,發牌人偷看底牌,並且發牌人在軟 17 點停牌。
二十一點——首次行動機率
| 行動 | 可能性 |
|---|---|
| 站立 | 43.46% |
| 打 | 39.78% |
| 雙倍的 | 9.53% |
| 分裂 | 2.48% |
| 二十一點 | 4.75% |
| 全部的 | 100.00% |
如果允許投降,那麼這個機率就是 4.14%,這是從站立的機率中得出的。
值得注意的是,邦德曾經在16對10的情況下停牌。基本策略是擊中它,但可能性很小。考慮到那手牌中出現了大量的10,邦德可能知道點數很高,這會觸發基本策略例外,在這種情況下停牌。
一手牌沒中機率是 60.22%。假設每手牌都是獨立的,那麼 15 手牌中 15 手牌沒中機率是 0.602162 15 = 0.000496253 = 大約 2015 年的 1 手牌。
在《魷魚遊戲》中,16 位玩家要透過一座玻璃橋進行遊戲。這座橋被分成 18 塊玻璃。每塊玻璃中,一塊是強化玻璃,可以支撐一名玩家的重量。另一塊是普通玻璃,會在玩家的重量下破碎。如果玩家踩到一塊普通玻璃,就會破碎並墜落身亡。
玩家必須按照預先指定的順序逐一前進。
假設隨機猜測每對玻璃台階,預計有多少玩家可以安全通過?
我會將答案和解決方案放在劇透標籤中,以便讓全世界的人都能自己找到答案。
[劇透=解]
玩家 1 安全過關的機率是 (1/2)^18 = 1/262144 = 約 0.000004。
玩家 2 可以透過兩種方式安全穿越:
- 玩家 1 安全過關。在這種情況下,玩家 2 只需複製他的步驟。
- 在玩家 1 和玩家 2 之間,只有一個錯誤步驟。這個錯誤步驟可能出現在 18 對可能的玻璃杯中。 17 個正確步驟和 1 個錯誤步驟的機率是 18*(1/2)^2 = 18/262144 = 0.000069。
因此,球員 2 安全傳球的機率為 0.000004 + 0.000069 = 0.000072。
玩家 3 可以透過兩種方式安全過河:
- 玩家 2 安全過關。在這種情況下,玩家 3 只需複製他的步驟。
- 在玩家 1、2 和 3 之間,只有兩個壞步驟。從 18 對玻璃中選出 2 個殺死玩家 1 和 2 的玻璃片,總共有 (18,2)=153 種方法。 16 個好步驟和 2 個壞步驟的機率為 153*(1/2)^2 = 153/262144 = 0.000584。
因此,球員 3 安全傳球的機率為 0.000072 + 0.000584 = 0.000656。
玩家 4 可以透過兩種方式安全過關:
- 玩家 3 安全過關。在這種情況下,玩家 4 只需複製他的步驟。
- 在玩家 1 到 4 之間,只有 3 個壞步驟。從 18 對玻璃中選擇 3 個來殺死玩家 1 到 3 的兩塊玻璃,總共有 combin(18,3)=816 種方法。 15 個好步驟和 3 個壞步驟的機率是 816*(1/2)^2 = 816/262144 = 0.003113。
依照這個邏輯,我們得到以下每位球員的機率表。
橋牌
| 玩家 | 可能性 生存 |
|---|---|
| 1 | 0.000004 |
| 2 | 0.000072 |
| 3 | 0.000656 |
| 4 | 0.003769 |
| 5 | 0.015442 |
| 6 | 0.048126 |
| 7 | 0.118942 |
| 8 | 0.240341 |
| 9 | 0.407265 |
| 10 | 0.592735 |
| 11 | 0.759659 |
| 12 | 0.881058 |
| 十三 | 0.951874 |
| 14 | 0.984558 |
| 15 | 0.996231 |
| 16 | 0.999344 |
| 全部的 | 7.000076 |
以封閉形式表達答案,即:
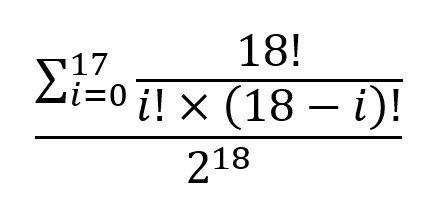
我在Wizard of Vegas論壇上提出並討論了這個問題。
在你的終極 X 金牌中,3:10 時你拿到了一張四點同花順,也就是三點和四點。你從 2 到 4 的任何四點同花的乘數是 9 倍。而葫蘆的乘數是 1 倍。為什麼你保留了四點同花順,而不是只保留三張 3,而是嘗試得到乘數更大的四點同花呢?
你說得對,我那隻手確實搞砸了。
回想一下,我玩的是10人玩法。因此,我拿到葫蘆的贏利是10×35 = 350。
僅持有三,每手牌都有以下機率:
- 四條 — 4.26%
- 滿堂彩——6.11%
- 三條 — 89.64%
以下是乘數之後每手牌的贏利:
- 四條 — 1800
- 滿堂彩——35
- 三條 — 15
如果只持有三條,我的預期收益將是 (4.26% * 1800) + (6.11% * 35) + (89.64% * 15) = 92.17854。這比葫蘆的 35 倍要高得多。所以,沒錯,我在那手牌上犯了一個尷尬的錯誤。
有人向我挑戰,要我進行以下賭注。我可以從一副標準撲克牌中選擇任意三個點數,寫下我的預測,但要保密到最後。例如,7-A-2。然後他提議和我打等額賭注,如果他猜對三次,他至少能猜出我的一個點數。我贏的幾率是多少?
要獲勝,對手的三次預測都必須全部錯誤。第一次預測有 10/13 的機率是錯誤的。第二次預測有 9/12 的機率是錯誤的,因為我們可以排除第一個猜測的排名的可能性。第三次預測有 8/11 的機率是錯誤的,因為我們可以排除前兩個猜測的排名的可能性。
這三件事必須同時發生,你才能獲勝。因此,你獲勝的機率是 (10/13) * (9/12) * (8/11) = 720/1716 = 41.96%。
在均等賭注下,從您的角度來看,這場賭注的莊家優勢是 16.08%(哎喲!)。
這個問題摘自歐文‧艾謝 (Owen E'Shea) 所著的《命題賭注之書》(第 7 期)。


