請問巫師 #338
使用兩個骰子,要獲得 2 到 12 的總數,平均需要擲多少次?
正方形中間有一隻螞蟻,它距離左上角17英寸,距離右上角20英寸,距離右下角13英寸。
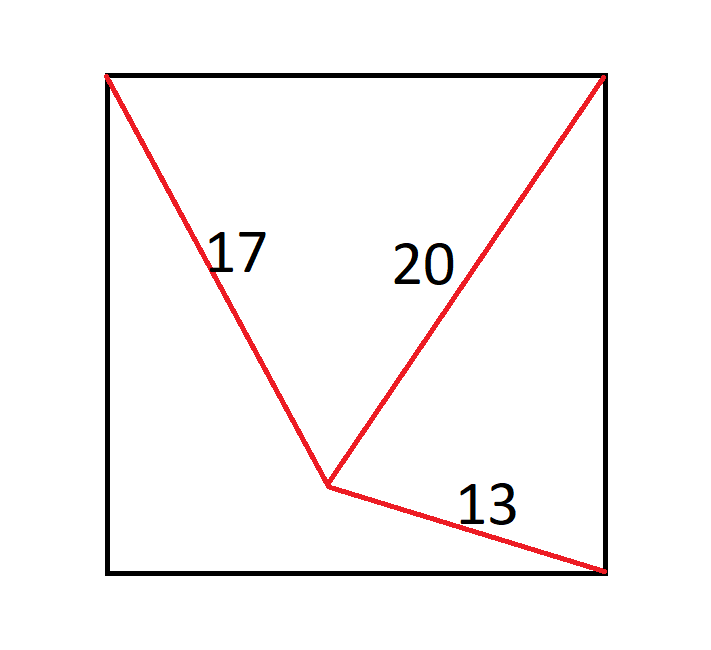
這個正方形有多大?
[劇透=有用的公式] c^2 = a^2 + b^2 -2ab*cos(c)
cos(a+b) = cos(a)*cos(b) - sin(a)*sin(b)
[劇透=解]
首先,將三角形ABE旋轉90度,形成新的三角形BDF。
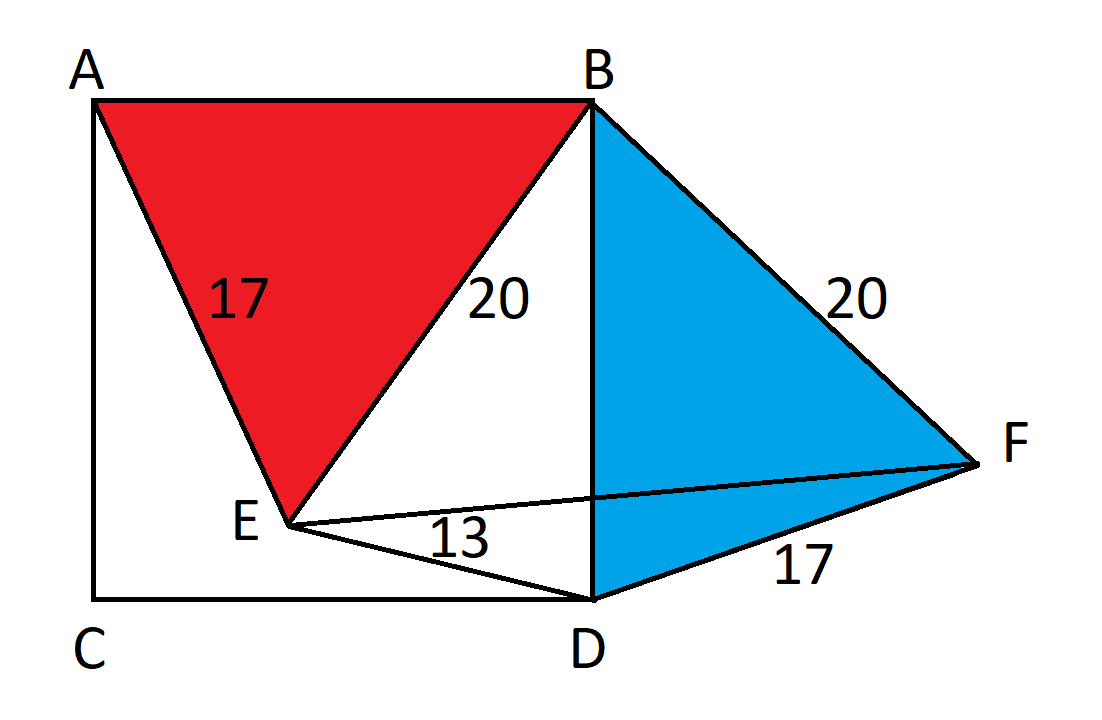
由於三角形旋轉了90度,根據定義,角EBF=90。根據勾股定理,EF = 20*sqrt(2)。
根據餘弦定律:17^2 = 13^2 + (20*sqrt(2))^2 - 2*13*20*sqrt(2)*cos(DEF)。
289 = 169 + 800 - 520*sqrt(2)*cos(DEF)
520*sqrt(2)*cos(DEF) = 680。
cos(DEF) = 17*sqrt(2)/26。
回想一下,sin^2(x) + cos^2(x) = 1。讓我們用它來解 sin(DEF)。
sin^2(DEF) + cos^2(DEF) = 1
sin^2(DEF) + (17*sqrt(2)/26)^2 = 1
sin^2(DEF) + 289/338 = 1
sin^2(DEF) = 49/338
sin(DEF) = 7*sqrt(2)/26
接下來,考慮角度 BED。
角度 BED = 角度 BEF + 角度 FED。
我們知道 EBF 是 90 度,並且是一個等腰三角形。這樣一來,角 BEF 就是 45 度。
因此,角度 BED = 45 度 + 角度 FED。
回想一下,cos(a+b) = cos(a)*cos(b) - sin(a)*sin(b)。
cos(BED) = cos(BEF + FED) = cos(BEF)*cos(FED) - sin(BEF)*sin(FED)
= (1/sqrt(2))*17*sqrt(2)/26 - (1/sqrt(2))*7*sqrt(2)/26
= (17/26) - (7/26) = 10/26 = 5/13
讓我們再次應用餘弦定律,這次針對三角形 BED。
BD^2 = 20^2 + 13^2 - 2*20*13*(5/13)
= 400 + 169 - 200 = 369
BD 是所討論正方形的邊長,因此 BD^2 是該正方形的面積,我們已經表明其面積為 369。
[/spoiler]我在Wizard of Vegas論壇上提出並討論了這個問題。
投擲死亡遊戲 (Drop Dead) 使用五個標準骰子進行。回合開始時,您需擲出所有五顆骰子。如果所有骰子都不是 2 或 5,則計算所有骰子點數總和,並將結果加到您的點數中,然後重新擲骰。如果擲出任何 2 或 5,則您的本輪得分為零。所有顯示 2 或 5 的骰子均視為死點,並作廢。然後,您使用剩餘的骰子重新擲骰。遊戲繼續,您可以選擇得分或移除骰子。當所有骰子都被移除後,您的回合結束,即您被判定為投擲死亡。所有得分將加在一起,作為您的最終得分。得分高者獲勝。
您對這場比賽的預期得分是多少?
[劇透=解]
讓我們從剩下一個骰子的場景開始並向後移動。
設變數 a 為剩餘一個骰子時的預期附加點數。
除 2 或 5 之外的平均擲點數為 (1+3+4+6)/4 = 7/2。
a = (2/3)×(a + 7/2)。
a/3 = 7/3。
a = 7。
接下來我們計算一下剩下兩顆骰子的預期點數b。
b = (2/3) 2 ×(b + 2 × (7/2)) + 2×(2/3)×(1/3)×a。
b = 11.2。
接下來我們計算一下剩下三個骰子的預期點數c。
c = (2/3) 3 ×(c + 3× (7/2)) + 3×(2/3) 2 ×(1/3)×b + 3×(2/3)×(1/3) 2 ×b。
c = 1302/95 = 13.705263。
接下來,我們來計算剩下四顆骰子的預期點數d。
d = (2/3) 4 ×(d + 4× (7/2)) + 4×(2/3) 3 ×(1/3)×c + 6×(2/3) 2 ×(1/3) 2 ×b + 4×(2/3)×(1/3) 3 ×a。
d = 3752/247 = 15.190283。
最後,我們來計算一下剩下五顆骰子的預期點數e。
e = (2/3) 5 ×(e + 5×(7/2)) + 5×(2/3) 4 ×(1/3)×d + 10×(2/3) 3 ×(1/3) 2 ×c + 10×(2/3) 2 ×(1/3) 3 ×b + ×(23/3 ) 。
e = 16.064662。
我在Wizard of Vegas論壇上提出並討論了這個問題。
以三張牌撲克中的對子加註為例,它遵循1-4-6-30-40的賠率表。然而,黑桃小皇家牌的賠率是累積獎金,其他三種花色的小皇家牌的賠率是累積獎金的25%。為了公平起見,計量表需要多高?


