WOO logo

Wizard 巫師推薦

請問巫師 #326

擲骰子遊戲中的鐵十字策略是什麼？您對此有何看法？

anonymous

鐵十字是一種投注場地和位置的方式，在擲出 7 以外的任何數字時都會獲勝。場地已經涵蓋了 2、3、4、9、10、11 和 12。玩家將在此基礎上加上 5、6 和 8 的位置投注，以覆蓋除 7 之外的其餘數字。下表顯示了場地投注 5 美元、5 美元位置投注 5 美元、6 美元位置投注 6 和 8 的數學計算情況。

鐵十字勳章

骰子總數贏組合可能性返回
2 10 1 0.027778 0.277778
3 5 2 0.055556 0.277778
4 5 3 0.083333 0.416667
5 2 4 0.111111 0.222222
6 2 5 0.138889 0.277778
7 -22 6 0.166667 -3.666667
8 2 5 0.138889 0.277778
9 5 4 0.111111 0.555556
10 5 3 0.083333 0.416667
11 5 2 0.055556 0.277778
12 15 1 0.027778 0.416667
三十六1.000000 -0.250000

表格右下角顯示預期損失為0.25美元。總投注金額為22美元。因此，總賭場優勢為0.25美元/22美元=1/88=1.14%。

說到這兒，你可能會疑惑，為什麼這個賭場優勢會低於每次投注的賭場優勢。答案是，投注6和8的賭場優勢為1.52%，投注5的賭場優勢為4.00%，這些優勢都是基於每次投注的。如果以每次投注為單位來定義位置投注的賭場優勢，那麼投注6和8的賭場優勢為0.46%，投注5的賭場優勢為1.11%。

我們可以對所有投注進行加權平均，得出 1.14% 的賭場優勢，如下所示：

（$5*2.78% + $5*1.11% + $12*0.46%）/22 = $0.25/$22 = 1.14%。

警惕那些在12點的場地投注中只支付2比1賠率的賭場。堅持要求獲得完整的3比1賠率。短賠率會使該投注的賭場優勢從2.78%翻倍至5.56%。

在我看來，與大多數遊戲相比，1.14% 的賠率已經相當不錯了。然而，在擲骰子遊戲中，你的賠率可以更高。例如，如果賠率為 3-4-5 倍，請下注 Pass 和 Come，再加上全賠率，你的賭場優勢可以降至 0.37%。反過來，下注 Don't Pass 和 Don't Come，再加上全賠率，賭場優勢就會降到 0.27%。

擲一個公平的骰子，每個面至少擲出兩次，預期擲骰子的次數是多少？

Ace2

答案是 390968681 / 16200000 = 約 24.13386919753086

[劇透=解]

雖然這個問題可以用冗長乏味的馬可夫鏈來解決，但我更喜歡用積分法。我在我的Fire Bet和Bonus Craps頁面中解釋瞭如何使用這種方法。

想像一下，重大事件不再由一次擲骰子決定，而是被視為一個時間瞬間。假設事件之間的時間間隔具有無記憶性，平均間隔為一個時間單位。換句話說，事件之間的時間間隔服從平均值為1的指數分佈。這對裁決賭注來說無關緊要，因為事件仍然是一次一個地發生的。

根據泊松分佈，在 x 個單位時間內，骰子任一面擲出次數為零的機率為 exp(-x/6)*(x/6) 0 /0! = exp(-x/6)。泊松分佈也表示，任一面擲出恰好一次的機率為 exp(-x/6)*(x/6) 1 /1! = exp(-x/6) * (x/6)。因此，任一面在 x 個單位時間內擲出兩次或兩次以上機率為 1 - exp(-x/6)*(1 + (x/6))。六面擲出至少兩次的機率為 (1 - exp(-x/6)*(1 + (x/6))) 6。至少有一面未擲出至少兩次的機率等於：

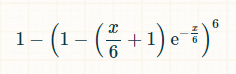
每面卷兩次

我們需要將其與所有時間結合起來，以找出平均需要多長時間才能實現預期目標。

幸運的是，我們此時可以使用積分計算器。對於連結中的那個，在「計算積分」後面的文字方塊中輸入 1- (1 - exp(-x/6)*(1 + x/6))^6 dx = apx. 24.1338692，並在自訂下將積分的邊界設為 0 到 ∞。

答案是 390968681 / 16200000 = 約 24.13386919753086

[/spoiler]

我在Wizard of Vegas論壇上提出並討論了這個問題。

我有一個由兩個部分組成的問題。

對於第 1 部分，給出：
  • x + y + z = 1
  • x^2 + y^2 + z^2 = 4
  • x^3 + y^3 + z^3 = 9

x^4 + y^4 + z^4 是多少？

對於第二部分，當出現以下情況時，一般情況的答案是什麼：

  • x + y + z = a
  • x^2 + y^2 + z^2 = b
  • x^3 + y^3 + z^3 = c

anonymous

問題 1：97/6 = 約 16.166666

問題 2：a 4 /6 + (4/3)ac - a 2 b + b 2 /2

[劇透=解]

請參閱我的解決方案（PDF）

[/spoiler]

這個問題是在我的「拉斯維加斯巫師」論壇中提出並討論的。

你先用一個公平的六面骰擲六次，記錄每次擲出的結果。然後，你把這些數字寫在另一個沒有標籤的公平骰子的六個面上。例如，如果你擲出的六次結果是3、5、3、6、1和2，那麼你的第二個骰子上就不會出現4，而是會出現兩個3。

接下來，你把第二顆骰子擲六次。把這六個數字寫在另一個公平骰子上，然後繼續這個過程，用前一個骰子產生一個新的骰子。

最終，你會得到一個六個面點數都相同的骰子。為了達到這個狀態，從一個骰子轉換到另一個骰子的平均次數是多少（或是總擲骰數除以6）？

rsactuary

約 9.65599148388557

[劇透=解]

為了避免混淆，我們用字母而不是數字來標記初始骰子。我們用字母標記每個可能的骰子狀態。例如，AAABBC 表示三個相同字母，兩個相同字母，一個相同字母。初始狀態顯然是 ABCDEF。

令 E(ABCDEF) 為從狀態 ABCDEF 開始的預期擲骰次數。

E(ABCDEF) = 1 + [180 × E(AAAAAB) + 450 × E(AAAABB) + 300 × E(AAABBB) + 1800 × E(AAAABC) + 7200 × E(AAABBC) + 1800 × E(AABBCC) + 7200 × E(AAABBC) + 1800 × E(AABB ×) + AAA ×BAA × E(AAABBC) + 1800 × E(AABB) + AAA ×BAA.202020000000000+) + 20202022229 × +202022) +2020202022) +20202,000 E(AABCDE) + 720 × E(ABCDEF)]/46656

基於從一個狀態到另一個狀態的組合數量，下面的轉換矩陣顯示了從每個初始狀態（左列）到每個新狀態的轉換方式數量。順便說一下，這花了幾個小時才建造好。

過渡矩陣A

狀態
前		啊啊啊啊AAAAB AAAABB AAABBB AAAABC AAABBC美國商務部商務合作委員會AAAABCD ABCD ABCDE ABCDEF
AAAAB 15,626 18,780 9,750 2,500 - - - - - - -
AAAABB 4,160 13,056 19,200 10,240 - - - - - - -
AAABBB 1,458 8,748 21,870 14,580 - - - - - - -
AAAABC 4,098 12,348 8,190 2,580 7,920 10,080 1,440 - - - -
AAABBC 794 5,172 8,670 5,020 6,480 17,280 3,240 - - - -
美國商務部商務合作委員會192 2,304 5,760 3,840 5,760 23,040 5,760 - - - -
AAAABCD 732 4,464 4,140 1,680 7,920 14,400 2,520 4,320 6,480 - -
ABCD 130 1,596 3,150 1,940 5,280 16,800 3,600 4,800 9,360 - -
ABCDE 68 888 1,380 760 3,960 11,520 2,520 7,200 14,040 4,320 -
ABCDEF 6 180 450 300 1,800 7,200 1,800 7,200 16,200 10,800 720

我不會長篇大論地講解矩陣代數，只是假設矩陣 B 如下：

矩陣B

狀態
前		AAAAB AAAABB AAABBB AAAABC AAABBC美國商務部商務合作委員會AAAABCD ABCD ABCDE ABCDEF
AAAAB -27876 9750 2500 0 0 0 0 0 0 -46656
AAAABB 13056 -27456 10240 0 0 0 0 0 0 -46656
AAABBB 8748 21870 -32076 0 0 0 0 0 0 -46656
AAAABC 12348 8190 2580 -38736 10080 1440 0 0 0 -46656
AAABBC 5172 8670 5020 6480 -29376 3240 0 0 0 -46656
美國商務部商務合作委員會2304 5760 3840 5760 23040 -40896 0 0 0 -46656
AAAABCD 4464 4140 1680 7920 14400 2520 -42336 6480 0 -46656
ABCD 1596 3150 1940 5280 16800 3600 4800 -37296 0 -46656
ABCDE 888 1380 760 3960 11520 2520 7200 14040 -42336 -46656
ABCDEF 180 450 300 1800 7200 1800 7200 16200 10800 -46656

答案是矩陣 B 的行列式與矩陣 A 的行列式之比：

確定（A）= 1,461,067,501,120,670,000,000,000,000,000,000,000,000,000,000,000

確定（B）= 14,108,055,348,203,100,000,000,000,000,000,000,000,000,000,000,000

Determ(B) / Determ(A) = 約 9.65599148388557

[/spoiler]