請問巫師 #322
我坐在一局德州撲克桌前,當牌局進行時,高手拿到了同花順。桌上另外兩位玩家說,這是連續第三張同花順。這機率是多少?
在一場10人參與的德州撲克遊戲中,假設無人棄牌,那麼高手牌為順子或同花大順的機率是350.14分之一。三局中有三局出現這種情況的機率是42,926,491分之一。
然而,那張牌桌可能已經玩了好幾個小時了。或許更現實的問題是,這種情況在一天中至少發生一次的機率是多少。假設整整24小時都在玩,每小時24手牌,那麼這個問題的答案是59,621分之一。
我在Wizard of Vegas論壇上提出並討論了這個問題。
假設策略正確,在終極德州撲克中,如果玩家加註4倍,獲勝的機率是多少?我記錄了96手4倍牌局。不算平局,我贏了66手,輸了30手。這與預期相比如何?
假設 4 倍加註策略正確,則在 4 倍加註的情況下,每個結果的機率為:
- 勝率:58.82%
- 虧損:38.47%
- 平手:2.72%
若排除平手因素,勝率是60.46%。在96手牌中,4倍勝的預期次數為58.04次。因此,66次勝率略高於預期,但幅度並不顯著。
我在Wizard of Vegas論壇上提出並討論了這個問題。
阿克塞爾和鮑伯各自有一副52張的牌。兩人都隨機洗牌。然後,他們同時從每副牌中翻出一張牌。他們同時翻出同一張牌至少一次的機率是多少?
答案很容易估算為 1-(51/52) 52 = 0.63568648。然而,估算在智力上實在難以令人滿意。所以,讓我們來求一個精確的解吧!
步驟 1:首先,考慮第二副牌的排序方式數,其中第一張牌是 1。答案是排序其他 51 張牌的方式數,即 51! = 1551118753287382280224243016469303211063259720016986112000000000000。
任何牌都能搭配第一副牌,所以我們必須對所有 52 張牌都進行相同的操作。這樣一來,就有 52*51! = 52! 種組合,其中至少有一張牌匹配。
步驟 2:然而,步驟 1 會重複計算兩張牌相符的所有情況。例如,如果前兩張牌是 1 和 2,那麼我們需要將其他牌的 50! 種排列方式計算兩次,第一次將 1 作為第一張牌,第二次將 2 作為第二張牌。從 52 張牌中選出 2 張牌的方式數為 combin(52,2) = 1326。每兩張牌的組合,其他牌的排列方式有 50! = 30414093201713378043612608166064768844377641568960512000000000000000 種。因此,對於步驟 2,我們需要減去 combin(52,2)*50! = (52*51/2!)*50! = 52!/2! 種組合。
步驟 3:接下來,考慮隨機牌堆中前三張牌的順序為 1、2 和 3 的情況。其餘 49 張牌有 49! 種排序方法。在初步步驟中,我們會數三次,以找出至少一張相符的牌。然後,在第二步驟中,我們會減去所有 combin(3,2)=3 種從這三張牌中選擇 2 張的方法。因此,這種情況會被計算 3-3=0 次,因此我們需要將它們加回去。有 combin(52,3) 種選擇至少 3 張配對牌的情況。因此,我們需要重新加入 combin(52,3)*49! = 52*51*50*49!/3! = 52!/3! 種組合。
步驟 4:接下來,考慮隨機牌堆中前四張牌的順序為 1、2、3 和 4 的情況。其餘 48 張牌有 48! 種排序方法。在初始計數至少一張匹配牌的步驟中,我們需要數四次。然後,在步驟 2 中,我們需要減去所有 combin(4,2)=6 種從這四張牌中選擇兩張的方法。然後,我們需要加上所有 combin(4,3)=4 種從這四張牌中選擇三張的方法。因此,每種情況都有 4-6+4=2 種計數方法。因此,我們需要減去其中一種計數方法,使每種情況都只計算一次。共有 combin(52,4)*48! = 52*51*50*49*48!/4! = 52!/4! 種需要加回去的情況。
我們將繼續這樣做,交替進行加法和減法來修正重複計算。
最後,隨機牌堆中至少有一張牌與有序牌堆匹配的情況數量 = combin(52,1)*51! - combin(52,2)*50! + combin(52,3)*49! - combin(52,4)*48! ... - combin(52,52)!1! = 52,4)*48! ... - combin(52,52)!1 52!/4! ... - 52!/52! = x = 333239808909468890675694068318655265019682314241643033726180828783。
共有 52 種方法可以排列 52 張牌! = y = 5271776154963652194226185415451226599692124538619822080000000000000 種方法可以排列 52 張牌。
因此,答案是 x/y = 0.6321205588285576784044762298
沒有匹配的機率是 1-(x/y) = 0.3678794411714423215955237702。
如果這個數字看起來很熟悉,那就對了。 1/e = 0.3678794411714423215955237702。
因此,答案可以非常接近地估計為 1-(1/e)。
致謝
數學計算是在Pari/GP中進行的
這個問題已在我的Wizard of Vegas論壇中提出並討論。
在您網站上名為賓果模式機率(PDF) 的文檔中,您指出,假設遊戲中有 300 張牌,那麼找到獲勝者的預期呼叫次數如下:
- 四角球:8.43
- 小鑽石:11.833
兩種模式都只需要四個標記,並且只有一種獲勝方式。為什麼獲勝所需的球數不同?
這個問題很難解釋。首先,我想說的是,單張牌遊戲中的預期叫牌次數是一樣的。然而,多張牌遊戲中存在相關效應。
這個問題很難快速回答,但如果硬要回答,那是因為四角圖案需要球集中在B列和O列。而小菱形圖案則更容易在B、N和O列上更均勻地分佈球。
讓我們把遊戲簡化成無限多張牌,每次抽球都會放回原位。以下是兩種遊戲中獲勝所需的球數:
- 四個角:2.5+2.5+((1/2)*10+(1/2)*(2.5+5)) = 13.75
- 小鑽石:=(5/3)+((1/3)*((5/3)+(5/2)+5)+(2/3)*((5/2)+((1/2)*((5/2)+5)+(1/2)*(5+5)))) = 12 + 2/9
這表明四個角球多花了 1.53 個球。
根據正常的賓果遊戲規則,透過模擬執行此程序,假設有無限張牌,結果如下:
- 四角:12.8289
- 鑽石:11.3645
這次相差 1.46 個球。
我希望展示的是,如果標記分佈在更多列上,圖案更容易被覆蓋。因此,我認為在單排賓果遊戲中,你通常會看到獲勝的賓果圖案是水平的。
這個問題是在我的「拉斯維加斯巫師」論壇中討論過的。
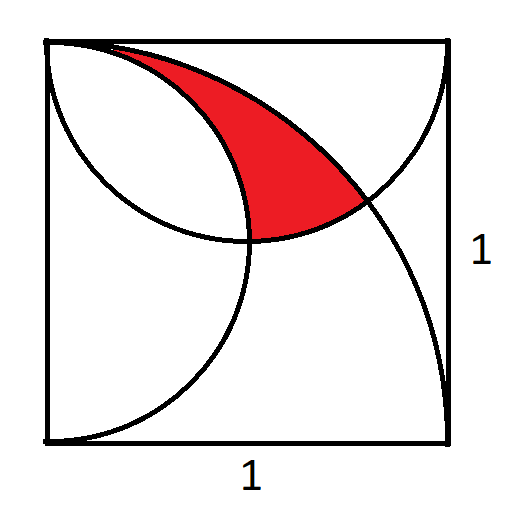
上圖中,邊長為1的正方形中有一個四分之一圓和兩個半圓。請問紅色區域的面積是多少?
點擊以下按鈕查看我的答案。
[spoiler=答案](3/8)*asin(4/5)-(1/4)=~0.0977357067506052[/劇透]點擊以下按鈕查看我的解決方案。
[劇透=解]這是我的解決方案的連結。 (PDF)
我在Wizard of Vegas論壇上提出並討論了這個問題。
致謝:我要感謝Mind Your Decisions提供這個數學謎題。


